变式教学在初中数学课堂的应用

广东省广州市第四中学(510360) 邓丽丽

变式教学在初中数学课堂的应用

广东省广州市第四中学(510360) 邓丽丽

所谓变式教学是指教师在引导学生解答数学问题时,变更概念非本质的特征,变更问题的条件或结论;转换问题的形式或内容;创设实际应用的各种环境,使概念或本质不变的一种教学方式.下面本人结合理论学习和数学课堂教学的实践,谈谈在数学教学中如何进行变式训练培养学生的思维能力.

一、一题多变,举一反三,加强学生对题目的理解,锻炼学生的逻辑思维能力.

案例1: 人教版八年级上册P93《复习题13》之“拓广探索”第14题

如图1,△ABC为等腰三角形,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G,求证:G为AB的中点.

图1

图2

变式1: 如图1,△ABC为等腰三角形,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF.求证:CF⊥AB.

变式2: 如图2,△ABC为等腰三角形,△BDC和△ACE分别为等边三角形,EA与DB延长线相交于点F,连接CF交AB于点G.求证:G是AB中点.

以上两个案例是条件与结论互换的变式,在变式探究的过程中,学生的思维逐步深入,有利于促进学生对知识本质的认识,对各种数学思想方法的熟练掌握,有利于培养学生思维的灵活性和深刻性.伽利略曾说过“科学是在不断改变思维角度的探索中前进的”.故而课堂教学要常新、善变,通过题目延伸出更多具有相关性、相似性、相反性的新问题,深刻挖掘例习题的教育功能.

案例2: 人教版八年级下册课本第68页复习题18第13题

如图3,在四边形ABCD中,AD//BC,B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B运动.规定其中一个运动到终点时,另一个也随之停止运动.从运动开始,使PQ//CD和PQ=CD,分别需经过多少时间?为什么?

变式1: 四边形PQCD是否能成菱形?若能,求出运动时间;若不能,请说明理由.

变式2: 四边形PQCD是否能成正方形?若能,求出运动时间;若不能,请说明理由.

这样的变式,有利于学生的思维逐步深入,有利于促进学生对知识本质的认识,培养学生思维的灵活性和深刻性.

图3

二、一题多解,触类旁通,通过变式培养学生发散思维能力,提高学生解决问题的能力.

一题多解的实质是以不同的论证方式,反映条件和结论的必然本质联系.在教学中教师应积极引导学生从各种途径,用多种方法思考问题.这样,既可暴露学生解题的思维过程,增加教学透明度,又能使学生思路开阔,熟练掌握知识的内在联系.通过一题多解,让学生从不同角度思考问题、解决问题,可以引起学生强烈的求异欲望,培养学生思维的灵活性.

案例1:如图4,点AB为圆O的直径,且点A为弧CD的中点,连接CD交AB于点E,求证:∠CAB= ∠DAB.(请用尽可能多的不同方法证明)

图4

引导学生灵活运用相关知识解决问题,归纳出圆中辅助线的常见构造方法以及证明角相等的常见方法.此题具备(一题多法),可引导学生用不同的方法求解.

方法一: 引导学生通过运用弧、弦、圆心角之间的关系进行求解,

方法二:结合本题的特征,通过垂径定理进行求解,

方法三:通过角平分线的判定定理求解,

方法四:通过构造全等进行求解.

案例2: 如图5所示,AB是⊙O的直径,C为弧AE的中点,CD上AB于点D,交AE于点F,连接AC,求证:AF=CF.(请用三种以上的不同的方法证明)

图5

图6

通过对案例1进行再一次的深入变式,让学生学会从不同角度看问题,加强知识和方法的灵活运用.

案例3: 如图6所示,已知在△ABC中,AB=AC,以BC为直径的圆O交边AB于点E,交边AC于点F.求证:BE=CF.(请用尽可能多的方法证明该结论,并总结证明线段相等的方法)

三、多题一解,求同存异.

通过变式让学生理解知识间的内在联系.许多数学练习看似不同,但它们的内在本质或者说是解题的思路,方法都是一样的,教师在教学中重视对这类问题的收集,比较,引导学生寻求通法通解,并让学生自己感悟它们之间的内在联系,形成解题的数学思想方法.

案例1:《人教版》八下P29拓广探索第13题

题目: 如图7,分别以等腰Rt△ACD的边AD、AC、CD为直径画半圆,求证:所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.

图7

图8

变式1: 如图8,以Rt△ABC的三边为边长向外作三个正方形,探索其面积S1、S2、S3之间的关系.

变式2: 如图9,分别以Rt△ABC三边为直径向外作三个半圆,探索其面积S1、S2、S3之间的关系.

图9

图10

上面通过变式,转换图形,使学生对勾股定理有深刻的理解,让学生意识到,只要向外作以三角形三边为对应边的相似图形即可.从而提高了思维的灵活性,深刻性,广阔性.

案例2:如图10,过正方形ABCD内部任意一点O作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,证明:EF=GH.

变式1: 在例题中,如果将点O移动到正方形外,如图11,其他条件不变,是否还类似的结论?结论如何表述?

图11

图12

解决变式1后,再对例题进行变化,提出如下问题:

变式2:如图12,已知O为矩形ABCD内一点,过点O作两条互相垂直的直线分别交矩形于点E,F,G,H,则EF与GH又存在着怎样的关系呢?

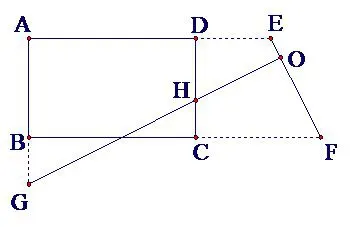
图13

变式3:把点O移到矩形ABCD外(如图13)是否还有同样的结论?结论又该如何表述?

总之,在教学中注重变式训练,可以促使学生的思维向多层次、多方向发散,帮助学生在问题的解答过程中去寻找解决类似问题的思路、方法,有意识地展现教学过程中教师与学生数学思维活动的过程,充分调动学生学习的积极性,培养学生独立分析和解决问题的能力.当然,课堂教学中的变式最好以教材为源,以学生为本,体现出“源于课本,高于课本”,并能在日常教学中渗透到学生的学习中去.引导学生从“变”的现象发现“不变”的本质,从“不变”的本质中探究“变”的规律.