数学素养的测量及评价

王娅婷，毛秀珍



数学素养的测量及评价

王娅婷1，毛秀珍2

（1．四川师范大学教师教育与心理学院，四川成都 610068；2．四川师范大学教育科学学院，四川成都 610068）

近年来，数学素养的探讨已经成为数学教育研究中的热点．围绕学生数学素养，探讨数学素养的测量与评价方法．首先梳理了国、内外数学素养的概念与构成要素，然后对数学素养的测量工具和数据分析方法进行详细的介绍和评述，最后面向未来对数学素养的发展提出一些思考．

数学素养；测量；数据分析

核心素养是当前教育领域的热词．强化学生的核心素养已成为未来基础教育的顶层理念[1]．《国家中长期教育改革和发展规划纲要（2010—2020年）》将树立科学的质量观，促进人的全面发展、适应社会需要作为衡量教育质量的根本标准[2]．之后2014年教育部印发的《关于全面深化课程改革，落实立德树人根本任务的意见》中，首次提出了“核心素养体系”的概念，明确强调了核心素养开始成为新一轮课程改革深化的方向，同时也界定关键能力和必备品格是构建终身学习，全面可持续发展的根基[3]．2016年9月13日，《中国学生发展核心素养》总体框架正式发布，在教育界引起巨大反响．

学生核心素养的培养分解在不同学科素养之中，需要通过不同的课程共同实现（辛涛，2016）[4]．数学作为人类文化的重要组成部分，已深刻渗透在生活的方方面面．数学的发展不单可以提高国民数学知识、能力水平以及解决实际问题的能力，还极大地推动了科学技术的进步．高中数学课程标准明确将数学核心素养定义为：学生应具备的能够适应终身发展和社会发展需要的、与数学有关的关键能力和思维品质．著名学者余文森（2016）指出：“通过厘清数学学科核心素养，清晰地界定和描述数学学科对人发展的价值和意义，体现数学学科对学生成长的独特贡献，从而使数学教育真正回到服务于人的发展的方向和轨道上来．”[5]

目前国内外有关学生数学素养的研究主要集中在4个方面：（1）数学素养内涵及构成要素的界定；（2）数学素养的测量与评价；（3）数学素养的现状及影响因素；（4）数学素养的生成和培养机制．这里将从数学素养的内涵和构成要素，以及测量工具和数据分析方法这几个方面的相关研究做出详细的介绍和评述，最后基于数学素养测评方法的发展提出一些思考．

1 数学素养的内涵及构成要素

“数学素养”概念的界定是最基本和核心的研究内容，对实现数学教育目标具有重要指导意义．中国学者已经对国内外数学素养的内涵和构成要素进行了深入的研究，康世刚（2009）指出20世纪70年代末以前，中国并没有明确地提出“数学素养”的名词，只是讨论与数学素养有关的教学问题；20世纪70年代末到1983年，都是随意地使用数学素养，也没有给予明确定义；自1983年以后，才开始将数学素养作为一个研究对象，讨论其涵义[6]．刘喆（2011）梳理了西方数学教育中数学素养概念的发展历程，将其归纳为3个发展阶段：20世纪60—80年代中后期是数学素养提出的早期阶段；80年代末期至90年代末期是数学素养的内涵不断拓展与丰富阶段；21世纪之后，数学素养的定义逐渐明晰、内涵走向综合，并指出“内容、过程和背景”是揭示数学素养内涵的3个主要部分[7]；之后胡典顺（2010）[8]和何小亚（2015）[9]也总结归纳了国内、外数学素养的缘起，发展和内涵演变历程．

通过对有关数学素养内涵的研究的梳理，归纳形成了3种主要观点：第一种看法从“素质”的角度入手：张奠宙教授（1994）提出：“数学素质包括知识观念、创造能力、思维品质和科学语言4个层面”[10]；王子兴（2002）将数学素养界定为数学科学方面的素质[11]；第二种观点将数学素养作为“能力”的综合，如束仁武（1997）提出数学素养是指运算能力、发展逻辑能力和空间观念，辨别、猜想能力等各种数学能力[12]，而刘俊先（2009）[13]和于凤艳（2010）[14]都强调了学生能够在日常生活中能够灵活地运用数学知识、基本技能和思想来解决实际问题的能力；最后一种观点也是目前最主流的看法，认为数学素养是动态发展的，是一个集合了数学的知识、能力和情感态度价值观的概念．马云鹏（2015）将数学核心素养概括为学生学习数学应当达成的有特定意义的综合性能力，其基于数学知识技能，又高于具体的数学知识技能，具有综合性、阶段性和持久性[15]；何小亚[9]和桂德怀、徐斌艳[16]也均概括性地指出数学素养是数学知识、能力和情感态度价值观的综合体．喻平教授通过实证研究，采用大样本问卷分析得到数学核心素养的两种结构，除数学抽象、运算能力、推理能力、数学建模、数据处理、空间能力、问题解决等能力外，还把数学文化品格这一要素纳入其中[17]．

2 数学素养的测量

厘清“数学素养”概念和构成要素是表征和刻画“数学素养”水平的基础．而“数学素养”的测量则是获取“数学素养”水平的手段和方法．下面将对目前研究中测量“数学素养”的工具和法则进行详细的介绍和评价．

2.1 国外对数学素养的测量方法

国际上有重要影响的测验有以下几种：国际学生评估项目（Program for International Student Assessment，PISA）[18]、国际数学和科学教育成就趋势研究（The Trends in International Mathematics and Science Study，TIMSS）[19]和美国全国教育进步评价（National Assessment of Education Progress，NAEP）[20]．这里对这3种测评项目进行了比较，具体见表1．

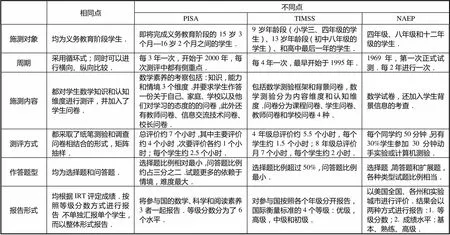
表1 “PISA”“TIMSS”和“NAEP”的比较

综合上述3种学业质量评价项目，可以发现它们在工具编制、测试内容、评价方式等方面都具有一定的相似性．首先，这些测评项目不但注重学生对于知识的掌握情况，还关注学生认知能力的发展；第二，评价工具除纸笔测验外，同时均加入了学生的背景问卷，不仅关注学生个体自身，还会从家庭、学校、社会等多方面进行考评，探索影响学生数学素养的因素；第三，这些测试框架形成时间悠久，发展比较成熟，考查题型类似；第四，测验信息的反馈也不拘泥于一个简单的分数，而是按照等级的方式，能够更好地用来指导学校教学工作的开展；最后，它们均运用了现代心理测量学理论指导试卷的编制和分析．但是3者也有一定的差异，比如TIMSS和NAEP注重对具体知识，概念和技能掌握程度的测评，但是PISA在题目设置上则对情境问题的依赖性较高，大部分题目都在考察学生能否在具体情境条件下运用自身的知识和能力来解决问题．这都是值得中国在课程设置与学业评价如测验编制、成绩反馈时借鉴和运用的有益经验．

此外，许多国家都建立和完善了本国的基础学业测评体系，如英国自1988年起对7、11、14和16岁学生国家课程各科目情况进行评定；澳大利亚从2008年推出全国性的评价项目（National Assessment Program，简称NAP），由联邦政府批准设立并划拨专款，对中小学3、5、7和9年级的各学科情况进行全面测评[21]．还有日本近年出现的《日本中小学生数学学力测验》和法国教育部评估司主办的《法国全国中小学诊断测验性数学评价》也可运用于“数学素养”的测量和评价[22]．

2.2 国内对数学素养的测量方法

为顺应全球教育改革的发展趋势与要求，中国基础教育也开始从“知识核心”逐步迈向“素养本位”时代．2015年，中国宣布实施国家义务教育质量监测体系，每3年为一个监测周期，每年监测两个领域，测试内容包括了义务教育阶段语文、数学、科学、体育、艺术、德育等领域中对阅读、写作、问题解决、科学探究、运动与健康、审美等相关素养的测评，被称为“中国特色的PISA”[23]．

目前，中国学者也积极开展对学生数学素养测评方式的探索，一类是学者直接采用国际上已有的数学素养测评系统对中国学生进行施测，文献[24~26]都采用了公开的PISA试卷和问卷调查学生的数学素养水平；另一类积极构建中国本土化的面向不同群体（如中小学生、高中生和数学师范生）的数学素养评价工具，基本思路都先将“数学素养”定义为可测量的维度，再围绕测评维度编制测验工具，最后对测验数据进行分析[27~30]．

为增强国家的竞争力，提高人才质量，中国亟需建立一套符合中国国情，完整、系统的测量框架，不但能充分了解学生的知识掌握情况、能力水平高低，并且还可以为教育实践活动和国家课程改革提供很多有利的建议．但中国大部分研究都直接采纳和编译国外测量工具，自编测量工具较少．很显然，国外现有测评工具由于文化差异、教育理念的不同以及课程重点等因素会导致直接编译的工具不能很好地反映中国实情，因此借鉴国内外技术和方法，编制一套符合中国实情、科学可靠的数学素养测评体系刻不容缓．

3 数学素养的数据分析理论与方法

从收集到的数学素养数据分析方法来看，目前大部分有关“数学素养”的研究都采用了经典测量理论进行数据分析和报告，也有部分研究运用了项目反应理论挖掘数据信息．下面将对各种数据分析方法进行评述．

3.1 经典测量理论下数学素养的分析

1968年洛德和诺维克提出经典测验理论（Classical Test Theory，CTT），即经典的真分数理论，将测验观察分数表示为真分数和误差分数之和．经典测量理论是标准化考试的理论支柱，其突出的优点是：理论和方法体系相对完整，前提假设比较弱，很容易为实际考试工作所满足；所涉及到的数学模型及参数的概念和估计方法容易被人理解和掌握；所提倡的标准化技术在控制测量误差等方面具有明显的效果（杨志明、张雷，2003）[31]．

目前传统测量理论已广泛应用到学生数学素养的分析中，主要包括两个方面的内容：项目特征（项目难度和区分度）和测验质量（测验的信、效度）．当前对“数学素养”试卷的项目分析，并得到了较好的测验信效度[32]．同时也有研究基于CTT理论分析学生个体在数学素养水平的差异，如针对不同性别以及不同民族学生的差异分析[24，26，30]．

尽管CTT简单易用，但是这也不可避免其在数据分析和报告方面的不足．例如，项目难度、区分度、信度和效度完全依赖于接受测验的被试样本能力．假如被试的水平越高（低），则项目的难度越小（大），区分度也会越低；同时被试样本组的能力分布又依赖于项目的难度，当项目的难度都很高（低），被试得分分布越集中，这样就会在一定程度上降低被试能力的估计准确性．因此，随着现代测量理论和计算机技术的迅速发展，研究者们开始运用新的理论方法进行数据分析和报告．

3.2 项目反应理论下数学素养的分析

美国测量学家F. Lord于1952年提出的项目反应理论（Item Response Theory，IRT）是在克服CTT局限性的基础上发展而来．它通过被试的潜在特质来预测和解释对项目和测验的反应行为，关注被试在某一任务领域的整体精熟程度[33]．IRT建立了包括测验项目参数，被试能力以及被试正确作答概率的数学函数，通过输入被试的作答反应，输出得到项目参数和被试的能力水平．常用软件有IRTPRO、Parscale、BILOG、Conqest等．

不同于CTT只报告测验分数，项目反应理论一方面能够对试题进行深入细致的分析，可以通过试题的特征曲线和信息量分析，测验目的以测量学的标准定义到测验目标信息函数上，从图形和数据的角度直接反映是否达到测验的目标，保证了测验的精度．测验目标信息曲线中两个重要的概念：项目信息曲线和测验信息曲线，首先项目信息曲线是关于项目信息函数的曲线，其大小由项目参数和被试特质水平决定，项目提供的信息量越大，表明这个项目在评价此被试特质水平时越有价值[34]；其次测验信息曲线是由项目信息曲线叠加而成，也即所有项目信息函数的累加和，它反映了整个测验在评价不同被试特质水平时的信息贡献关系，测验提供的信息量越大，测量标准误就越小，则该测验在评价该被试特质水平时越精确[35]．

另一方面，同时通过项目反应理论可以获得试题的参数，包括难度、区分度和被试的能力参数．由于IRT假设项目参数估计独立于被试样本，不依赖于被试群体的能力的分布．换句话而言，不需担心因被试群体的改变，导致项目的难度会有变化．另外，IRT可以通过模型估计被试的能力水平，并估计测量误差，充分提高了测验的信度．因此进一步确定什么能力水平的考生能对试题做出正确的应答，对哪些考生具有良好的区分能力，试题的质量是否良好．

当前IRT越来越广泛深入到测评领域，其优势也日益得到认识．国际上大型测评项目都运用IRT分析和报告测量数据．例如，OECD在公布PISA测验的数据结果时，均会采用IRT统计学生得分并设计了6个能力水平，水平由低到高，每个水平都规定了具体能达到的要求．国内，采用IRT理论和技术分析数学素养的测评报告已不再新鲜．例如，卢光辉（2007）运用三参逻辑斯蒂克模型分析数学素养调查试卷的项目，采用BILOG对项目和被试群体的参数进行估计[24]．

可见，IRT分析的结果提供的信息量远远大于CTT的原始分数报告，其测量也更符合实际情况．依据IRT理论不仅可以指导测验编制，提高测验本身的信、效度质量，还能充分利用项目信息，更加准确地估计被试能力．

3.3 多维项目反应理论下数学素养的分析

随着项目反应理论在实际测验中的广泛应用，人们逐渐发现很少有测验只测量单一维度或特质水平[36]．多维项目反应理论（Multidimensional Item Response Theory，MIRT）正是基于IRT单维性假设的限制应运而生．MIRT引入多维能力、多维项目区分度以及多个步骤难度参数模拟测验项目和被试间的相互作用，采用概率模型来表征具有特定多维能力水平的被试正确答对特定项目的概率（Reckase，2009）[37]．它实现了同时估计被试多个能力维度的值，可以深入分析被试在测验每个维度上的表现，进而实现认知诊断功能（Zhang & Stone，2008）[38]．可以预见到MIRT的应用顺应了从2001年美国法案“No Child Left Behind”（NCLB）到2011“Race to the top”早期学习挑战经费的设立，再到中国《国家中长期教育改革和发展规划纲要（2010—2020）年》对教育认知诊断功能的要求，是今后研究与实践发展的趋势．

MIRT是基于因子分析和IRT的双重背景下发展起来的新型测验理论，关注被试在测验多个领域的能力水平．例如，Yao和Schwarz（2006）运用多维项目反应理论分析了五年级学生写作测验的二维结构和项目特征[39]；涂冬波、蔡艳、戴海琦和丁树良（2011）运用MIRT证实瑞文高级推理测验数据满足多维性结构[40]；张军（2011）运用MIRT分析了中国汉语水平考试（HSK）中阅读部分的潜在多维度结构[41]．因此，IRT在实际测验中不总是适用的，对许多测验如认知诊断测验、公务员考试、表现性评估、写作测验等，MIRT都更适于分析测验和被试特征（van der Linden & Hambleton，1997）[42]．目前对于数学素养的测验还没有应用多维项目反应理论进行诊断，但可以预见到多维项目反应理论具有广泛的应用前景，也更为适用于分析“数学素养”这类多维特质型测验．

3 小结与展望

当前，学生数学素养的测评已经成为各国测验的研究热点和教育者关注的重点．国际测评发展历史悠久，并且形成比较完善的测评体系，在许多国家得到应用和推广．但是，也要关注到各国都还缺乏一套适合于本国各个学段，具备统一、完整结构的数学素养测评体系．

中国没有真正意义实现全面系统地测量学生数学素养：目前要么直接采用现有国际测评项目，经验证这些测验对中国学生施测时得到较好的信效度．由于项目特定评价对象的要求，在中国实行只能是对等同年级的学生．再加上国际评价侧重点与中国教学实际仍有一定的差距，如中国课程设置上更加关注知识和技能方面的培养，测评维度也有差异，若直接照搬忽视了中国的本土化特点；要么自编的数学素养测评工具，其优势在于能够对于不同年龄阶段学生、具体数学领域进行测评．但目前对数学素养在概念界定和维度划分上差异很大，具体采取测评的形式不一．在这种背景下，中国有必要汲取国际测验的新思路和理念，结合中国实际国情，构建中国学生数学素养测评的框架体系和数学素养评价系统．因此借鉴国内外工具和方法编制一套符合中国实情，科学、可靠的数学素养测评体系刻不容缓．

另外，关于数学素养的大部分研究以经典测量理论为依据对学生数学素养进行测量和评价，随着测量理论和计算机技术的发展，经典测量的缺陷也日益突出：对不同的被试进行施测，得到测验分析结果会有很大差异，导致测验项目的难度、区分度以及信效度都会有差异．因此，采用新的测量理论除了能克服CTT的缺陷外，在指导测量工具的编制和提高测量数据分析准确性上都具有明显的优势．同时，现代测量理论基于数学模型的方法分析数据，提高了学生能力水平的估计精度．最后，采用多维项目反应理论可以同时获得学生在多个维度上的能力水平，较以前的测验总分的报告更准确和详细，除了能更加准确地获得测量结果，还可以更加明确项目更适合哪种能力水平的考生作答，能更好地组织试卷，提高测验的质量．因此，在未来的研究中学者可以尝试利用MIRT对学生数学素养进行分析．

作为学生所必备的素养之一，数学素养决定了义务教育阶段的数学教育必须面向全体学生，为每一位学生的终身发展奠定基础．因此在数学素养的测量和评价上，必须积极创新、与时俱进，形成具有中国特色的数学素养测评体系，并借助现代测量技术，为现代数学教育提供指导和方向．

[1] 林崇德．对未来基础教育的几点思考[J]．课程·教材·教法，2016，（3）：3-6．

[2] 中共中央国务院．国家中长期教育改革和发展规划纲要（2010—2020年）[EB/OL]．http://www.moe.edu.cn/ publicfiles/business/htmlfiles/moe/moe_838/201008/93704.html

[3] 中华人民共和国教育部．教育部关于全面深化课程改革落实立德树人根本任务的意见[EB/OL]．http://www.moe. ov.cn/ublicfiles/business/htmlfiles/moe/s7054/201404/167226.html

[4] 辛涛．学生发展核心素养研究应注意几个问题[J]．华东师范大学学报（教育科学版），2016，（1）：6-7．

[5] 余文森．从三维目标走向核心素养[J]．华东师范大学学报（教育科学版），2016，（1）：11-13．

[6] 康世刚．数学素养生成的教学研究[D]．西南大学，2009．

[7] 刘喆．论师范生数学素养[D]．华南师范大学，2011．

[8] 胡典顺．数学素养研究综述[J]．课程·教材·教法，2010，（12）：50-54．

[9] 何小亚．学生“数学素养”指标的理论分析[J]．数学教育学报，2015，24（1）：13-20．

[10] 张奠宙．数学教育研究导引[M]．南京：江苏教育出版社，1994．

[11] 王子兴．论数学素养[J]．数学通报，2002，（1）：6-9．

[12] 束仁武．充分利用“想一想”培养学生的数学素养[J]．中学数学，1997，（11）：10-12．

[13] 刘俊先．论数学史对提高数学素养的重要作用[J]．教育与职业，2009，（24）：175-176．

[14] 于凤艳，张胜利．数学课程标准下学生数学素养的再认识[J]．现代教育科学·普教研究，2010，（3）：46-48．

[15] 马云鹏．关于数学核心素养的几个问题[J]．课程·教材·教法，2015，（9）：36-39．

[16] 桂德怀，徐斌艳．数学素养内涵之探析[J]．数学教育学报，2008，17（5）：22-24．

[17] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[18]  OECD. Assessing Scientific PISA2003 Technical Report [EB/OL]. http://www.pisa.oecd.org/pages

[19] IEA. The TIMSS 2007 international assessment design [EB/OL]. http://timss.bc.edu/TIMSS2007/PDF/T07_AF_ chapter4.pdf, 2008.

[20] NAEP Civics Consensus Project.[R]. Washington, DC: U.S.Department of Education, 1996.

[21] 占盛丽，文剑冰，朱小虎．全球化背景下PISA在美国基础教育质量评估体系中的贡献[J]．外国中小学教育，2010，（5）：1-6．

[22] 孔企平．国际数学学习测评：聚焦数学素养的发展[J]．全球教育展望，2011，（11）：78-82．

[23] 国务院教育督导委员会办公室．国家义务教育质量监测方案[EB/OL]．http://www.ec.js.edu.cn/art/2015/4/23/ rt_10347_170979.html

[24] 卢光辉．八年级学生数学素养测量与评价研究[D]．西北师范大学，2007．

[25] 肖云霞．基于PISA的高二学生数学素养的调查研究[D]．南京师范大学，2014．

[26] 李建美．巍山县彝族八年级学生数学素养现状的调查研究[D]．云南师范大学，2015．

[27] 梁策力．六年级学生数与代数素养测量与评价研究[D]．西南大学，2015．

[28] 齐宇歆．基于PISA的学习素养评价系统设计[D]．华东师范大学，2013．

[29] 王光明，张楠，周九诗．高中生数学素养的操作[J]．课程·教材·教法，2016，（7）：50-55．

[30] 刘喆．数学师范生数学素养现状的调查研究[J]．数学教育学报，2012，21（5）：23-40．

[31] 杨志明，张雷．测评的概化理论及其应用[M]．北京：教育科学出版社，2003．

[32] 盛秋玲．基于TIMSS 2011数学测验框架的小学数学试题研究——以上海市小学三、四年级为例[D]．上海师范大学，2014．

[33] 金瑜．心理测量[M]．上海：华东师范大学出版社，2005．

[34] 罗照盛，欧阳雪莲，漆书青，等．项目反应理论等级反应模型项目信息量[J]．心理学报，2008，（11）：1 212-1 220.

[35] 漆书青，戴海琦，丁树良．现代教育与心理测量学原理[M]．北京：高等教育出版社，2002．

[36] 康春花，辛涛．测验理论的新发展：多维项目反应理论[J]．心理科学进展，2010，（3）：530-536．

[37]  Reckase M D.[M]. New York: Springer, 2009.

[38]  Zhang B, Stone C A.[A]. Paper Presented at the Annual Meeting of the American Educational Research Association, San Diego, CA, 2004.

[39]  Yao L, Schwarz R D. A Multidimensional Partial Credit Model with Associated Item and Test Statistics: An Application to Mixed-Format Tests [J]., 2006, (37): 3-23.

[40] 涂冬波，蔡艳，戴海琦，等．多维项目反应理论：参数估计及其在心理测验中的应用[J]．心理学报，2011，（11）：1 329-1 340．

[41] 张军．HSK潜在维度的探索性分析——多维项目反应理论的应用[J]．考试研究，2011，（29）：47-58．

[42]  va n der Linden W J, Hambleton R K.[M]. New York, 1997.

[责任编校：周学智]

Measurement and Analysis of Students’ Mathematical Literacy

WANG Ya-ting1, MAO Xiu-zhen2

(1. College of Teacher Education and Psychology,Sichuan Normal University, Sichuan Chengdu 610068, China;2. College of Education, Sichuan Normal University, Sichuan Chengdu 610068, China)

In recent years, the research of mathematical literacy has become a hot spot in the research of mathematics education. So this paper focus on the students mathematical literacy to explore its measurement and evaluation methods. First, carding the concept of national and international mathematical literacy and elements, Then introduced and reviewed the measurement methods of mathematical literacy in detail , Finally based on the development of the mathematical literacy put forward some reflection.

mathematical literacy; measurement; data analysis

G40-03

A

1004–9894（2017）03–0073–05

2017–01–20

国家自然科学基金青年项目——多维计算机化自适应测验的研究与应用（31400897）

王娅婷（1992—），女，山西晋中人，硕士研究生，主要从事教育与心理测量、评价研究．毛秀珍为本文通讯作者．