浅谈数形结合方法在高中数学教学中的应用

杨源+李铁

摘要：师者，“传道、授业、解惑者也”，老师在给學生上课的过程中，为了尽最大可能激发出学生的学习兴趣，就不能一味地按照传统教学手法，对知识的教授生搬硬套，要以图文并茂的形式讲课。尤其是高中的数学老师，更要对这一方法进行深刻理解并掌握，因为，高中阶段使学生一生中重要的转折点，甚至直接影响学生以后的前途，而数学作为高中的三大主科之一，对学生在考大学的时候更是影响重大。但是，现阶段大多数的高中生都对数学存在一种恐惧心理，觉得学术性太强，甚至是反感数学，因此，数学老师就要在课堂中国有效运用数形结合的方法，提升学生的学习兴趣和理解能力。本文就数形结合思想在高中数学教学中的应用进行分析。

关键词：数形结合 初中数学 数学教学

数与形都是数学课堂上经常用到的教学方法，两者互为补充、各有要点，共同辅助同学进行学习。数可以从本质上体现事物之间的联系，形则体现相互关联事物之间的外在形式，带有简洁、直观的特点。也就是说数形结合的方式就是在对一个问题进行分析的过程中，把内在本质与外在条件充分结合，把数字归纳与直观的图形进行融合运用，帮助学生更快的解决问题。

一、数形结合思想在高中数学中的教学原则

（一）主体性原则

高中数学中合理的运用数形结合的方法，首先要把握其整体性的原则，不断带动学生发挥主观能动性。第一，教师要与时俱进，更新教学理念和方法，不要一味地以自己的意识为主导，对学生进行强制灌输教育，应该以学生为本，努力活跃课堂气氛，使每个学生主动参与到讨论中去；第二，教师应该全方位了解学生，运用课堂测验的办法掌握学习的基础情况，因材施教，让学生全面掌握并运用数形结合思想。

（二）渗透性原则

我们都知道，数学相较于其他学科来说，知识抽象化，每个学生在解题的时候遇到的障碍也不一样，因此，在普及数形结合理念的时候要秉持渗透性原则。要求老师对教材进行仔细研究，适时的引入数形结合思想，渗透到解题思路中去，使学生做到数形之间的自由转换。

（三）启发性原则

启发性原则的运用就要求老师在教学中提供更多的解题思路加上适当的引导，实现数形的有效结合和自由转换。课堂上，可是可以运用多样化的教学方式对学生起到引导作用，使他们明确数学理论与图形之间的内在联系，并学会灵活运用。比如在学习“平行线及其判定”时，教师可以画出多样的平行线，启发学生自己总结、判定，运用数学理论实现数形结合的有效掌握。

二、数形结合在初中数学教学中的运用

（一）在数学概念教学中数形结合思想的应用

在高中阶段的数学学习中需要掌握很多不同的概念性知识，而数学上的大概大多是抽象的不具体的，所以，老师在进行讲解的过程中往往不能面面俱到，学生在理解的时候面临的难度更大，所以，在数学课堂上，在碰到的诸多概念性问题的时候，学生大多会选择传统的方法，死记硬背的学习并运用，但是收效甚微。因此，再进行数学概念方面的教学中，老师完全可以运用数形结合的思想，用图像的表达方式对理论知识进行讲解，比如在讲授对称抽的概念中，选择一个目标图像，沿一条直线完成折叠，直至完全重合，如此，就可以清晰直观的对这一概念进行解释。由于高中阶段学生的思维能力还没得到完全成熟，教师运用理论结合图形的讲解方法，促进学生快速理解概念，并且进行合理利用。

（二）数形结合思想在实际教学中的应用

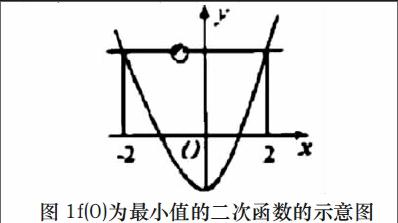
相信每一位教育工作者和数学教师或多或少都会对数形结合思想有了解，但是，在实际中该如何正确运用才能达到预期的效果，是大家一直在思考的问题。笔者经过多年的研究发现，在高中数学课堂上最具有典型代表性的数形结合例子就是抽象函数问题，再进行这类问题的计算过程中难倒了很多学生，特别是这种题以选择或者填空的形式出现，要是采用大量计算公式解答一定会耽误后面做大题的时间，因此，有效的运用数形结合思想就可以做到化繁为简，提高解题的效果。例如f（x）为二次函数，且其在f（0）的时候取最小值。现已知f（a）

因为f（x）为二次函数，开口向上，那么a的取值显而易见，通过科学、灵活的运用数形结合的解题思路，我们就可以把问题进行具体化、简单化，这样既节省了解题时间，也提高了正确率。我们学习数学的主要目的就在于更高效、更准确的解决问题，在实际教学活动中，也要坚持这种思想，将具体的内容通过引导的方式让学生领会到此种思想的重要性，还要鼓励他们把这种思想进行传播、弘扬。

（三）数形结合的运用在数学问题中的应用

数形结合的运用在解决直线以及圆锥曲线等中的有着很大的作用，主要概括为几个关键词，用数、代数式、方程表示关键点等。数形结合方法可以直观地表示直线倾斜程度，这样更容易让学生理解数学知识。例如，从形这一角度对直线倾斜角度进行刻画就可以让学生直观地看到直线具体的倾斜角度。而从数这一角度对直线的倾斜角度进行刻画就能通过数字的计算来探究。通过数形结合的方法能使学生更容易掌握知识，保证学生学习成绩的进步。

三、结语

总而言之，由于高中阶段的数学课本涉及到的知识都很抽象，学生在学习、运用的过程中都会明显感觉到吃力，在考试环节也无法取得满意的成绩，因此，教师就应该科学理论的应用数形结合思想，在讲课中把复杂的问题简单化、抽象的概念具体化，通过简单明了的绘图方式，让学生真正做到理解题目，为解题过程提供思路，同时，也培养学生的逻辑思维，有利于综合素质的提升。

参考文献：

[1]武俊英.数形结合思想在初高中数学教学中的实践研究[D].陕西师范大学，2014.

[2]李春长.谈数形结合在高中数学中的应用[J].课程教育研究，2015，（02）.

（作者单位：[1]杨源，内蒙古鄂尔多斯市准格尔旗世纪中学；[2]李铁，内蒙古包头市土右旗民族第一中学。）