刚性吊杆-水平抗风索耦合系统弯曲振动自振特性分析

赵 洋, 徐 凯, 汪志昊, 陈惟珍

(1. 同济大学 桥梁工程系， 上海 200092； 2. 华北水利水电大学 土木与交通学院， 郑州 450011)

刚性吊杆-水平抗风索耦合系统弯曲振动自振特性分析

赵 洋1,2, 徐 凯2, 汪志昊2, 陈惟珍1

(1. 同济大学 桥梁工程系， 上海 200092； 2. 华北水利水电大学 土木与交通学院， 郑州 450011)

将1对水平抗风索对钢拱桥刚性吊杆的约束作用简化为4个水平弹簧支撑，推导了抗风索等效弹簧刚度计算公式；基于欧拉-伯努利连续梁理论与吊杆-水平抗风索连接位置处的相容连续性条件，建立了刚性吊杆-水平抗风索耦合系统弯曲振动自振特性分析理论模型，通过与有限元结果对比验证了该方法的准确性；明确了水平抗风索位置、刚度参数对H型、矩形刚性吊杆纵桥向弱轴弯曲振动自振特性的影响规律。研究结果表明：合理设计的抗风索对H型、矩形刚性吊杆弱轴弯曲基频均有较大程度的提升，证实了抗风索对刚性吊杆弯曲模态减振的可行性；抗风索位置不同，对吊杆弱轴弯曲基频的影响程度也不同，且位置参数直接决定了吊杆弯曲基频增长极限值；相对H型吊杆，附加抗风索的矩形吊杆弱轴弯曲基频提升潜力更大。研究成果对钢拱桥刚性吊杆弯曲模态振动控制的水平抗风索减振参数优化设计具有重要参考价值。

刚性吊杆； 水平抗风索； 等效弹簧； 弯曲振动； 自振频率； 振型

钢桁架拱桥具有造型美观、跨越能力强等突出特点，近年来在我国得到较快发展。H型和矩形截面刚性吊杆是其常用的吊杆形式，但长细比大、阻尼低的该类吊杆易诱发多种风致振动病害[1-5]，工程实践通常采用气动、机械阻尼和水平抗风索这三类控措施来提高刚性吊杆的气动稳定性。气动措施[6-9]需根据风洞试验优化吊杆断面改善吊杆气动外形，但试验周期长，费用高且减振效果有限；机械阻尼措施[10-11]多在吊杆内部安装调谐质量阻尼器(Tuned Mass Damper, TMD)，通过增大吊杆附加阻尼减小风振幅值，但存在吊杆复杂边界条件下的TMD失谐、鲁棒性等问题；水平抗风索减振措施采用辅助索将多根吊杆串联，增大吊杆刚度，提高吊杆-抗风索耦合系统的自振频率进而增大吊杆风致振动起振风速，典型工程应用有美国Tacony Palmyra桥H型吊杆、加拿大Peace River桥圆形吊杆[12]以及国内佛山东平大桥H型吊杆。虽然水平抗风索减振措施具有诸多优点，也已在工程中得到广泛应用，但既有抗风索研究主要针对斜拉桥拉索的辅助索[13-14]减振，文献调研尚未发现吊杆-水平抗风索耦合系统自振特性理论分析模型及其求解方法。此外，抗风索减振措施目前仅用于H型吊杆扭转颤振控制、圆形吊杆弯曲振动控制，矩形吊杆则多采用TMD减振。因此，建立刚性吊杆-水平抗风索耦合系统弯曲振动理论分析模型，开展抗风索减振措施对矩形吊杆的可行性与适用性研究，明确抗风索参数对吊杆弯曲振动特性的影响规律，具有重要的工程应用价值。

本文将抗风索对吊杆的刚度增强作用简化为弹簧弹性支承，推导了抗风索等效弹簧刚度计算公式；基于欧拉-伯努利连续梁理论，结合吊杆-抗风索连接处的弯曲相容连续性条件，建立了刚性吊杆-水平抗风索耦合系统(后文简称吊杆-抗风索耦合系统)弯曲振动自振特性分析理论模型，并得到了有限元方法的验证；明确了抗风索位置、刚度参数对吊杆弯曲振动基频与振型的影响规律，可为吊杆减振用抗风索参数优化设计提供重要参考。

1 吊杆-抗风索耦合系统弯曲振动理论模型

1.1 吊杆-抗风索耦合系统

针对实桥刚性吊杆纵桥向弱轴弯曲基频低的特点，抗风索在纵桥向将各吊杆串联，抑制吊杆绕弱轴的弯曲振动。以工程中常见的开口H型和闭口矩形截面吊杆为例，建立H型、矩形刚性吊杆-抗风索耦合系统理论模型，如图1所示。

图1 吊杆-抗风索耦合系统

吊杆一般与主拱肋及桥面系通过高强螺栓连接，连接处刚度大，理论模型中将吊杆边界条件简化为两端固结。将1对水平抗风索对吊杆弱轴弯曲振动(y方向)的约束作用简化为吊杆两侧4个水平弹簧弹性支承[13]，并假设其弹性支承刚度分别为k1、k2、k3和k4；在弹性支承位置X1处，吊杆全长L被分为两段，分别为l1、l2，有X1=l1/L；吊杆弱轴(y方向)弯曲振动位移用yi(x,t)描述，i表示第i段吊杆，i=1,2；t为时间；H型吊杆腹板、翼板宽高及厚度尺寸分别为a1、b1、t1、w1，矩形吊杆宽、高及壁厚分别为a2、b2、t2、w2；N为吊杆两端轴向拉力。

1.2 吊杆弯曲振动微分方程

实桥刚性吊杆长细比大，阻尼小，可忽略吊杆转动惯量、剪切变形及固有阻尼对吊杆弯曲自振频率的影响，由此将吊杆简化为轴向力作用下的两端固结欧拉-伯努利梁。

假设吊杆运动为符合平截面假定的弯曲振动，根据欧拉-伯努利连续梁理论[15-17]，取吊杆任一x处截面微元dx，则轴向力作用下吊杆微元dx的弯曲振动受力如图2所示。

由图2列出吊杆振动y方向力的动平衡方程及关于c点(吊杆横截面与中性轴交点)的力矩平衡条件：

(1)

图2 刚性吊杆微元

(2)

联立式(1)和式(2)可得吊杆弯曲振动微分方程：

(3)

1.3 抗风索等效弹簧刚度

抗风索对矩形吊杆的弹性支承作用(H型吊杆与此相同),如图3所示，可将吊杆在同一截面处受到4个水平弹性支承的约束作用等效为1个刚度为K的等效弹簧。

图3 抗风索对矩形吊杆受力分析

由图3可知，吊杆在抗风索位置X1处受到的水平弹性支承作用力为

(4)

吊杆在抗风索位置X1处的等效弹簧平衡方程为

(5)

(6)

1.4 吊杆-抗风索耦合系统弯曲模态自振特性求解

根据结构动力学分离变量法[18]，第i段吊杆弯曲振动水平位移yi(x,t)的通解可表示为：

(7)

式中：φi(x)为第i段吊杆弯曲振动模态振型函数，i=1，2；ω为吊杆-抗风索耦合系统弯曲自振圆频率。式(7)代入式(3)可得：

(8)

由式(8)解得φi(x)：

φi(x)=Aisin(δx)+Bicos(δx)+Cisinh(εx)+Dicosh(εx)

(9)

式中：

Ai、Bi、Ci、Di为第i段吊杆实常数。

吊杆弯曲振动在抗风索位置X1处的位移、斜率、弯矩和剪力的相容连续性条件[19-20]分别为

(10)

(11)

(12)

(13)

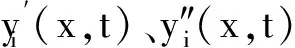
式(7)代入式(10)～(13)，吊杆相容连续性条件可化简为

(14)

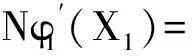
吊杆两端固结边界条件[21]可表示为

(15)

将式(9)分别代入式(14)、(15)并联立写为矩阵形式：

(16)

式(16)中：

R12=

R21=

式中：λ1=δ3+δ，λ2=ε3-ε；ψ为待定参数向量，ψ=[A1B1C1D1A2B2C2D2]T。

若使得方程具有非平凡解，则有

(17)

式(17)中，只有ω一个未知数，通过MATLAB软件编程并利用Newton-Raphson 公式，可求得吊杆-抗风索耦合系统弯曲自振圆频率ω，将ω代入式(16)可得各段吊杆振型参数ψ，从而根据式(9)可获得整段吊杆振型，基本计算流程，见图4所示。

图4 程序流程图

2 有限元分析与验证

2.1 吊杆与抗风索参数

(a) H型吊杆

(b) 矩形吊杆

分别选取某两座钢桁架拱桥的H型、矩形刚性吊杆，截面尺寸如图5所示，基本参数见表1。抗风索采用fpk=1 860 MPa，7φs15.2 mm钢绞线，弹性模量Ep=1.95×105MPa，泊松比γ=0.3，密度ρ=8 600 kg/m3。

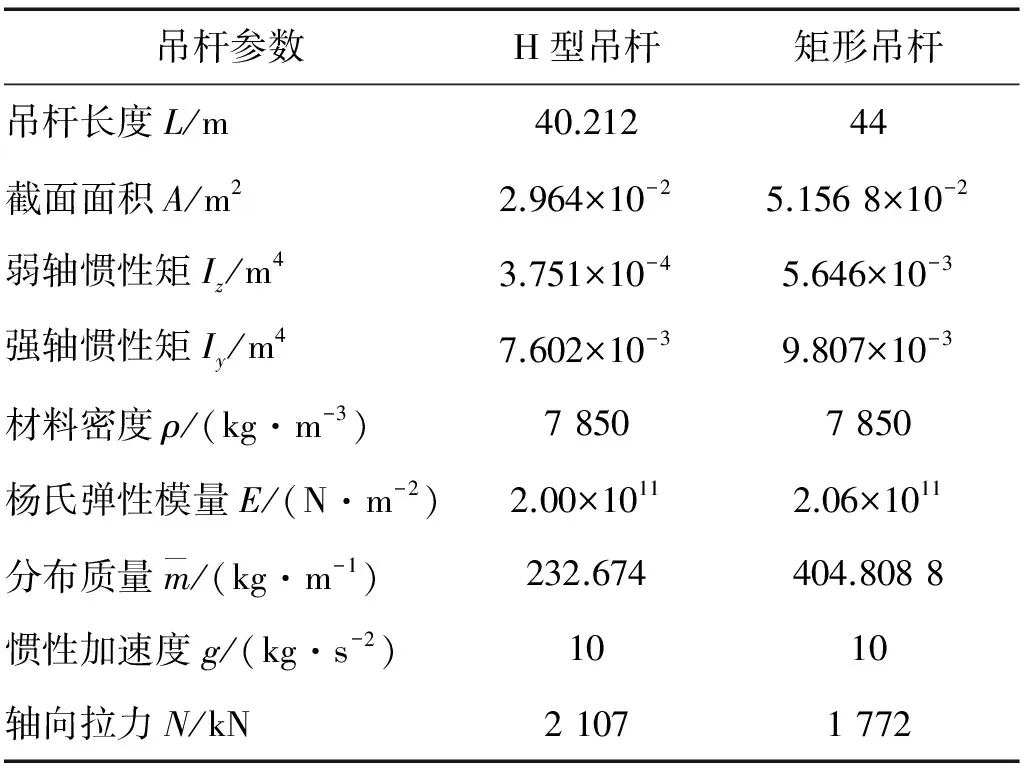
表1 吊杆基本参数

2.2 吊杆-抗风索耦合系统有限元模型

吊杆壁厚与特征尺寸比值很小，忽略剪切变形及转动惯量的影响，采用SHELL63壳单元模拟(图6)。吊杆边界条件处理为高强螺栓区一端固结，另一端释放轴向自由度并施加轴向荷载初位移ΔL模拟轴力几何刚度对吊杆弯曲自振频率的影响，ΔL为实桥抗风索采用夹片式锚具将其锚固于主拱肋两侧的锚块[22]。抗风索采用LINK10杆单元模拟，边界条件两端固结，通过设置初应变实常数模拟抗风索初张力。抗风索与吊杆一般采用索卡连接，有限元建模忽略两者的接触摩擦作用，以耦合重合节点的方式处理。

(18)

(a)H型吊杆⁃抗风索耦合系统(b)矩形吊杆⁃抗风索耦合系统

图6 吊杆-抗风索耦合系统有限元模型

Fig.6 Finite element model of the coupled system with a hanger and wind-resistant cables

2.3 吊杆第1阶弯曲自振频率与振型验证

取ζ=1 092 kN/m1作为抗风索等效弹簧刚度K的基准值，此时对应的抗风索长度lp=200 m，截面面积Ap=1.4×10-5m2(0.1根前述规格钢绞线)。以工程中最为关心的吊杆弱轴第1阶弯曲模态为例，分别采用本文理论方法与有限元计算抗风索位置、刚度参数分别为l1/L=0.25、0.5，K=10ζ、100ζ时的吊杆弯曲模态自振频率与模态振型，见图7及表2、3所示。表3中的“弯曲模态振型平均误差”指的是在x/L∈[0,1]区间等间距取100个数据点，所有数据点对应理论解与有限元结果振型数据误差的代数平均值。

(a) H型吊杆

(b) 矩形吊杆

由表2可知，各工况下所求得的吊杆第1阶弯曲自振频率理论解与有限元结果误差很小，均不超过2%；图7与表3可见，吊杆第1阶弯曲振型的理论解与有限元曲线也高度吻合，弯曲模态振型平均误差极小，均未超过0.5%。可见，本文所述理论方法对求解吊杆-抗风索耦合系统第1阶弯曲自振频率及相应振型具有较高的精度。

表2 吊杆第1阶弯曲自振频率对比

表3 吊杆第1阶弯曲模态振型平均误差

3 吊杆-抗风索耦合系统弯曲振动自振特性

3.1 抗风索位置、刚度参数对吊杆第1阶弯曲自振频率的影响

基于第2节H型、矩形吊杆参数信息，采用本文理论方法，分析吊杆第1阶弯曲自振频率随抗风索位置、刚度参数的变化规律，如图8所示。图中f1为吊杆第1阶弯曲自振工程频率，有f1=ω/2π。由图可见：

(1) 随着抗风索位置和刚度变化，H型、矩形吊杆第1阶弯曲自振频率曲线具有相同的变化趋势：同一抗风索位置l1/L处，吊杆第1阶弯曲自振频率均随抗风索等效弹簧刚度K的增大而增大，前期增长较快(H型：K≤10ζ；矩形：K≤20ζ)，后期增幅逐渐减小直至出现多曲线重合(H型：K≥50ζ；矩形：K≥500ζ)，此时吊杆第1阶弯曲自振频率趋于极限值；抗风索等效弹簧刚度K一定时，抗风索越靠近吊杆中心位置处，吊杆第1阶弯曲自振频率曲线斜率越大，增幅越大，并于x=0.5L取得最大值。抗风索等效弹簧刚度K越大，对吊杆的约束作用越强，吊杆第1阶弯曲自振频率越大，当抗风索位于吊杆中心位置(l1/L=0.5)，此为吊杆第1阶弯曲振型节点坐标最大处，抗风索对吊杆的约束作用最强，频率提高值最大。

(2) 同一抗风索位置处，矩形吊杆第1阶弯曲自振频率曲线随K的增加变化较为均匀，各频率曲线间距逐渐减小，当K≥500ζ后各曲线近乎重合；H型吊杆在K≥50ζ后即出现多部分重合，即较小的抗风索等效刚度即可使得H型吊杆第1阶弯曲自振频率达到极限值，而矩形吊杆第1阶弯曲自振频率极限值所对应的抗风索等效刚度远大于H型吊杆。

可见，当优先控制吊杆第1阶弱轴弯曲振动时，抗风索宜设置在吊杆中心位置处，此时吊杆第1阶弯曲自振频率提升显著。因此，后文仅针对抗风索位于吊杆中心位置处这一特殊情况(以下简称：吊杆-中点抗风索耦合系统)，对吊杆第1阶弯曲自振频率及振型随抗风索等效弹簧刚度的变化规律开展研究。

(a) H型吊杆

(b) 矩形吊杆

3.2 吊杆-中点抗风索耦合系统第1阶弯曲自振频率随抗风索等效弹簧刚度的变化规律

图9 吊杆第1阶弯曲自振频率随抗风索等效弹簧刚度K的变化

分析图9结果可知：

(1) H型、矩形吊杆第1阶弯曲自振频率均随抗风索等效弹簧刚度K的增加逐渐增大，开始增长较快，后期逐渐变缓并趋于极限稳定值，该值为H型和矩形原型吊杆1/2长度的第1阶弯曲自振频率，则H型吊杆第1阶弯曲自振频率最大可提高到原值的3.12倍，矩形吊杆可提高到原值的3.76倍，增幅明显，充分说明了抗风索不仅适用于H型吊杆，对矩形吊杆第1阶弯曲自振频率的提高也具有显著效果，进一步验证了抗风索对两种截面形式吊杆的适用性、可行性。

(2) 抗风索等效弹簧刚度较小时(K≤20ζ)，H型吊杆第1阶弯曲自振频率的增幅大于矩形吊杆；随着K的增大(K≥100ζ)，H型吊杆第1阶弯曲自振频率逐渐趋于稳定，而矩形吊杆第1阶弯曲自振频率继续增加并超越H型吊杆；H型、矩形吊杆分别对应K取100ζ、1 000ζ时达到准稳定值，这是由于H型吊杆弱轴抗弯刚度相对矩形吊杆偏小(表1)，附加较小的抗风索等效弹簧刚度即可取得频率极限值。

3.3 吊杆-中点抗风索耦合系统第1阶弯曲振型随抗风索等效弹簧刚度的变化规律

吊杆-中点抗风索耦合系统H型和矩形吊杆第1阶弯曲振型随抗风索等效刚度的变化规律如图10所示，可见：

(1) 随着等效弹簧刚度K的增大，H型、矩形吊杆振型幅值最大值位置均由x=0.5L逐渐变为x=0.25L和0.75L两处；等效弹簧刚度K越大，吊杆振型节点坐标φ(0.5)数值越小，并逐渐趋近于0。K越大，对吊杆的约束作用也越强，当大于某一阙值时，吊杆在此处趋于固结，弯曲模态位移接近0，吊杆变为完全独立的两段，这就进一步解释了3.2节中吊杆第1阶弯曲自振频率极限值与吊杆1/2长度对应的弯曲基频完全相等的现象。

(2) H型吊杆在K=ζ时φ(0.5)逐渐减小，而矩形吊杆在K=ζ时几乎无任何变化；K=500ζ时，H型吊杆在抗风索位置处已经嵌固，φ(0.5)=0，矩形吊杆在K=104ζ时固结，两者K值相差较为悬殊。

(b) 矩形吊杆

4 结 论

本文建立了刚性吊杆-水平抗风索耦合系统弯曲振动自振特性分析理论模型，研究了抗风索位置、刚度参数对吊杆-抗风索耦合系统第1阶弱轴弯曲自振频率及振型的影响规律。主要结论如下：

(1) 抗风索位置参数对H型和矩形吊杆第1阶弯曲自振频率极限值起决定性作用，抗风索位置越靠近吊杆端部，频率增量越小，而当接近吊杆中点位置时，频率增量显著。

(2) 本文算例中H型、矩形原型吊杆第1阶弯曲自振频率可分别提高到原值的3.12倍、3.76倍，2种吊杆弯曲自振频率均大幅提升。因此，抗风索不仅适用于H型吊杆扭转模态减振，对吊杆弱轴弯曲振动抑制也具有一定的可行性。

(3) 抗风索位于H型、矩形吊杆中点位置处，且等效弹簧刚度K大于某一阙值时，抗风索位置处吊杆近似固结，此时吊杆第1阶弯曲自振频率接近原吊杆1/2长度时的第1阶弯曲自振频率，且H型吊杆所需的抗风索等效弹簧刚度阙值远小于矩形吊杆。

[1] 马存明, 廖海黎, 郑史雄, 等. H型截面吊杆气动性能的风洞试验[J]. 中国铁道科学, 2005, 26(4): 42-46.

MA Cunming, LIAO Haili, ZHENG Shixiong, et al. Wind tunnel experiment on the aerodynamic performances of H-shaped booms[J]. China Railway Science, 2005, 26(4): 42-46.

[2] 周帅, 陈政清, 牛华伟. 矩形细杆涡振幅值和驰振性能的对比风洞试验[J]. 中国公路学报, 2014, 27(1): 64-75.

ZHOU Shuai, CHEN Zhengqing, NIU Huawei. Comparative experiment on vortex-induced vibration amplitude and galloping of slender rectangular cylinder[J]. China Journal of Highway and Transport, 2014, 27(1): 64-75.

[3] DING Y L, AN Y H, WANG C. Field monitoring of the train-induced hanger vibration in a high-speed railway steel arch bridge[J]. Smart Structures and Systems, 2016, 17(6):1107-1127.

[4] KELLER P, HIGGINS C, LOVEJOY S C. Evaluation of torsional vibrations in steel truss bridge members[J]. Journal of Bridge Engineering-ASCE, 2015, 20(9): 04014102.

[5] 许福友, 丁威, 姜峰, 等. 大跨度桥梁涡激振动研究进展与展望[J]. 振动与冲击, 2010, 29(10): 40-49.

XU Fuyou, DING Wei, JIANG Feng, et al. Development and prospect of study on vortex-induced vibration of long-span bridges[J]. Journal of Vibration and Shock, 2010, 29(10): 40-49.

[6] CHEN Z Q, LIU M G, HUA X G, et al. Flutter, galloping, and vortex-induced vibrations of H-Section hangers[J]. Journal of Bridge Engineering-ASCE, 2012, 17(3): 500-508.

[7] 刘慕广,陈政清. 典型钝体断面大攻角下的颤振自激力特性[J]. 振动与冲击, 2013, 32(10): 22-25.

LIU Muguang, CHEN Zhengqing. Characteristics of self-excited forces in flutter of typical blunt body under large attack angles[J]. Journal of Vibration and Shock, 2013, 32(10): 22-25.

[8] 刘慕广, 陈政清. 箱型吊杆的风致振动特性[J]. 工程力学, 2013, 30(3): 233-238.

LIU Muguang, CHEN Zhengqing. Wind-induced vibration characteristics of box suspender[J]. Engineering Mechanics, 2013, 30(3): 233-238.

[9] 陈政清, 刘慕广, 刘光栋, 等. H型吊杆的大攻角风致振动和抗风设计[J]. 土木工程学报, 2010, 43(2): 1-11.

CHEN Zhengqing, LIU Muguang, LIU Guangdong, et al. Wind-induced vibration and wind-resistant design of H-Section hangers under large attack angles[J]. China Civil Engineering Journal, 2010, 43(2): 1-11.

[10] 李荣庆, 朱世峰, 李东超. 新型吊杆减振器(TLMD)在南京大胜关大桥中的应用[J]. 世界桥梁, 2012, 40(6): 68-72.

LI Rongqing, ZHU Shifeng, LI Dongchao. Application of new type of TLMD to hangers of Dashengguan Changjiang River Bridge in Nanjing city[J]. World Bridges, 2012, 40(6): 68-72.

[11] 雷旭, 牛华伟, 陈政清, 等. 大跨度钢拱桥吊杆减振的新型电涡流TMD开发与应用[J]. 中国公路学报, 2015, 28(4): 60-68.

LEI Xu, NIU Huawei, CHEN Zhengqing, et al. Development and application of a new-type eddy current TMD for vibration control of hangers of long-span steel arch bridge[J]. China Journal of Highway and Transport, 2015, 28(4): 60-68.

[12] CARL C. Aerodynamic lessons learned from individual bridge members[J]. Annals of the New York Academy of Sciences, 1980, 352(1): 265-281.

[13] ZHOU H J, YANG X, SUN L M, et al. Free vibrations of a two-cable network with near-support dampers and a cross-link[J]. Structural Control and Health Monitoring, 2015, 22(9): 1173-1192.

[14] IZZI M, CARACOGLIA L, NOE S. Investigating the use of targeted-energy-transfer devices for stay-cable vibration mitigation[J]. Structural Control and Health Monitoring, 2016, 23(2): 315-332.

[15] VERNIERE DE IRASSAR P L, FICCADENTI G M, LAURA P A. Dynamic analysis of a beam with an intermediate elastic support[J]. Journal of Sound and Vibration, 1984, 96(3): 381-389.

[16] SHAHBA A, RAJASEKARAN S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials[J]. Applied Mathematical Modelling, 2012, 36(7): 3094-3111.

[17] MAIZ S, BAMBILL D V, ROSSIT C A, et al. Transverse vibration of Bernoulli-Euler beams carrying point masses and taking into account their rotatory inertia: Exact solution[J]. Journal of Sound and Vibration, 2007, 303(3): 895-908.

[18] MOHAMMADNEJAD M. New analytical approach for determination of flexural, axial and torsional natural frequencies of beams[J]. Structural Engineering and Mechanics, 2015, 55(3): 655-674.

[19] 郁殿龙, 温激鸿, 陈圣兵, 等. 轴向载荷周期结构梁的弯曲振动带隙特性[J]. 振动与冲击, 2010, 29(3): 92-95.

YU Dianlong, WEN Jihong, CHEN Shengbing, et al. Flexural vibration band gaps in axially loaded periodic beam structure[J]. Journal of Vibration and Shock, 2010, 29(3): 92-95.

[20] 崔灿, 蒋晗, 李映辉. 变截面梁横向振动特性半解析法[J]. 振动与冲击, 2012, 31(14): 85-88.

CUI Can, JIANG Han, LI Yinghui. Semi-analytical method for calculating vibration characteristics of variable cross-section beam[J]. Journal of Vibration and Shock, 2012, 31(14): 85-88.

[21] LIN H P, CHANG S C. Free vibration analysis of multi-span beams with intermediate flexible constraints[J]. Journal of Sound and Vibration, 2005, 281(1): 155-169.

[22] 四川省交通厅公路规划勘察设计研究院. 拱桥吊杆抗风减振构造:CN201962594U[P]. 2011-09-07.

Free flexural vibration characteristics analysis of a rigid hanger-horizontal wind resistant cables coupled system

ZHAO Yang1,2, XU Kai2, WANG Zhihao2, CHEN Weizhen1

(1. Department of Bridge Engineering, Tongji University, Shanghai 200092, China; 2. School of Civil Engineering and Communication, North China University of Water Resources and Electric Power, Zhengzhou 450011, China)

The restriction effects generated by a pair of horizontal wind resistant cables on a rigid hanger of a steel arch bridge were simplified as four equivalent springs. Then, the calculation formula for the equivalent spring stiffness of wind resistant cables was deduced. Based on Bernoulli-Euler beam theory and compatibility and continuity conditions of the connection position of the rigid hanger and horizontal wind resistant cables, a theoretical model for free flexural vibration characteristics analysis of a rigid hanger-horizontal wind resistant cables coupled system was established. The correctness of the theoretical model was verified through comparing its results and those of the finite element method. Finally, the effects of position and stiffness parameters of horizontal wind resistant cables on free flexural vibration characteristics of rigid hangers with H-type cross-section and rectangle-type one in longitudinal weak-axis direction were clarified. It was shown that the flexural vibration fundamental frequency in weak-axis direction of the two types hangers increases obviously due to reasonable design of wind resistant cables, so wind resistant cables are feasible for flexural vibration control of rigid hangers; the effect of wind resistant cables on the flexural fundamental frequency of the hangers varies with their different positions, the limit value of increase in the flexural fundamental frequency of the hangers is dependent upon position parameters of wind resistant cables; comparing with H-type hangers, rectangle-type hangers adding wind resistant cables have a larger potential to increase their flexural fundamental frequency in weak-axis direction. The study results provided a reference for optimal design of parameters of horizontal wind resistant cables to control flexural vibration of rigid hangers of steel arch bridges.

rigid hanger; horizontal wind-resistant cable; equivalent spring; flexural vibration; natural frequency; modal shape

国家自然科学基金(51308214)；国家重点基础研究973计划(2015CB057702)；河南省教育厅科学技术研究重点项目(13A560711)；河南省高校科技创新团队支持计划(15IRTSTHN028)；河南省高等学校青年骨干教师资助计划(2015GGJS-104)

2016-07-20 修改稿收到日期：2016-09-12

赵洋 男，博士生，副教授，1978年10月生

陈惟珍 男，博士，教授，1962年11月生

TU311.3

A

10.13465/j.cnki.jvs.2017.11.014