质量比对刚性圆柱体涡激振动影响的研究
2017-06-19陈正寿赵宗文张国辉颜盛汉
陈正寿, 赵宗文, 张国辉, 郑 武, 颜盛汉
(1.浙江海洋大学 船舶与机电工程学院,浙江 舟山 316022; 2.浙江省近海海洋工程技术重点实验室,浙江 舟山 316022; 3.太平洋海洋工程(舟山)有限公司,浙江 舟山 316057;4.浙江欧华造船股份有限公司,浙江 舟山 316101)
质量比对刚性圆柱体涡激振动影响的研究
陈正寿1,2, 赵宗文1, 张国辉1, 郑 武3, 颜盛汉4
(1.浙江海洋大学 船舶与机电工程学院,浙江 舟山 316022; 2.浙江省近海海洋工程技术重点实验室,浙江 舟山 316022; 3.太平洋海洋工程(舟山)有限公司,浙江 舟山 316057;4.浙江欧华造船股份有限公司,浙江 舟山 316101)
基于CFD方法,开展了质量比对刚性圆柱体涡激振动影响的研究。对低质量比分别为1和2.4和高质量比为7的刚性圆柱体分别进行双自由度涡激振动流固耦合模拟,得到了不同质量比工况下无因次振幅与约化速度之间的相关性,圆柱体的“8”字形运动轨迹以及“差拍”、“相位转换”等现象;初步的研究结果表明,低质量比的模型对应的振动锁振区范围要广于高质量比的模型,产生的横流向最大无因次振幅也较大,涡激振动现象更为显著。另外通过不同质量比对顺、横流向耦合振动影响的分析发现,在质量比为1和2.4时,顺流向振动对横流向振动产生的影响不容忽略,而在质量比为7时,其影响较小。另在涡激振动尾流区,捕捉到了“2S”、“2P”型泻涡发放。
质量比;涡激振动;流固耦合;刚性圆柱体
随着海上油气资源开发利用不断向深水推进,对深海管线系统的振动特性分析与安全性评估提出了更高的要求。在刚性圆柱体尾流泻涡脱落以及对应的涡激振动形态研究领域,Feng[1]首先提出刚性圆柱体弹性支撑的实验模型,并对大质量比的圆柱体进行了实验研究。Vikedtad等[2]研究了单自由度的弹性支撑圆柱体的涡激振动特性,得到了涡激振动振幅的变化规律。Sanchis等[3]研究了低质量比的两自由度圆柱体涡激振动形态,认为质量比是影响圆柱体振动特性的重要因素。Khalak等[4]研究了低质量阻尼比的弹性支撑刚性圆柱体,给出了无因次振幅与约化速度之间的联系。另有曹淑刚等[5]探讨了不同质量比对涡激振动的影响,并对顺流向频率进行了研究。与此领域相关的前期研究工作大多着眼于质量比对圆柱体单自由度涡激振动特性影响,而对双自由度模型与质量比对顺-横流向耦合振动影响的程度,相关研究成果比较少,另外对结构振动形态的分析,大都没有真正从流固耦合的角度进行全面的分析。本文在前人研究的基础上,利用CFD—CFX软件对质量比分别为1、2.4和7的刚性圆柱体进行双自由度流固耦合数值模拟,分析无因次振幅随约化速度的变化规律;阐明不同质量比、相同约化速度条件下刚性圆柱体单双自由度的振动特性,分析顺流向振动对横流向振动影响的程度;同时辅以尾流区的泻涡发放形态对涡激振动特性进行综合分析。
1 数值计算方法
1.1 涡激振动相关参数
(1) 升力系数、阻力系数
(1)
(2)
式中:Cl、Cd分别为升力系数、阻力系数与,Fy(t)是圆柱体所受的升力,Fx(t)是所受阻力,A为圆柱体的横截面积。
(2) 约化速度
(3)
式中:约化速度Ur是指每个振动周期的路径长度与圆柱体直径的比值,U为来流速度,fn为系统固有频率,D为圆柱直径。
(3) 质量比
(4)
式中:m*为圆柱质量比,是指模型质量对其所排开流体的质量之比,m为模型质量,md为所排开水的质量。
1.2 湍流模型选择
1997年Spalart提出了分离涡模拟(Detached Eddy Simulation,DES)的概念,这是一种同时融合了雷诺平均湍流模拟(RANS)与大涡模拟(LES)优点的新型湍流模型,其同时兼备了计算量小和准确性高的优点。它首先在近壁面附面层内采用RANS方法模拟小尺度脉动运动,另外采用类似LES方法模拟远离物的区域。相当数量的实际计算结果分析发现,DES能准确地和高效模拟钝体绕流流场,具有很高的优越性,应用前景广阔[6-8]。本文相关数值仿真计算均基于DES湍流模型完成。
1.3 结构控制方程及模型简化
本文基于研究质量比对圆柱体涡激振动特性影响的考虑,暂未将结构阻尼纳入振动方程。因此可将刚性圆柱体涡激振动简化为质量—弹簧系统,其控制方程如下:
(5)
(6)
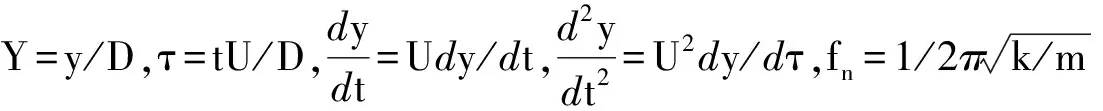
(7)
(8)
模型简化为弹性支撑的圆柱体如图1所示,分别为单、双自由度涡激振动简化。
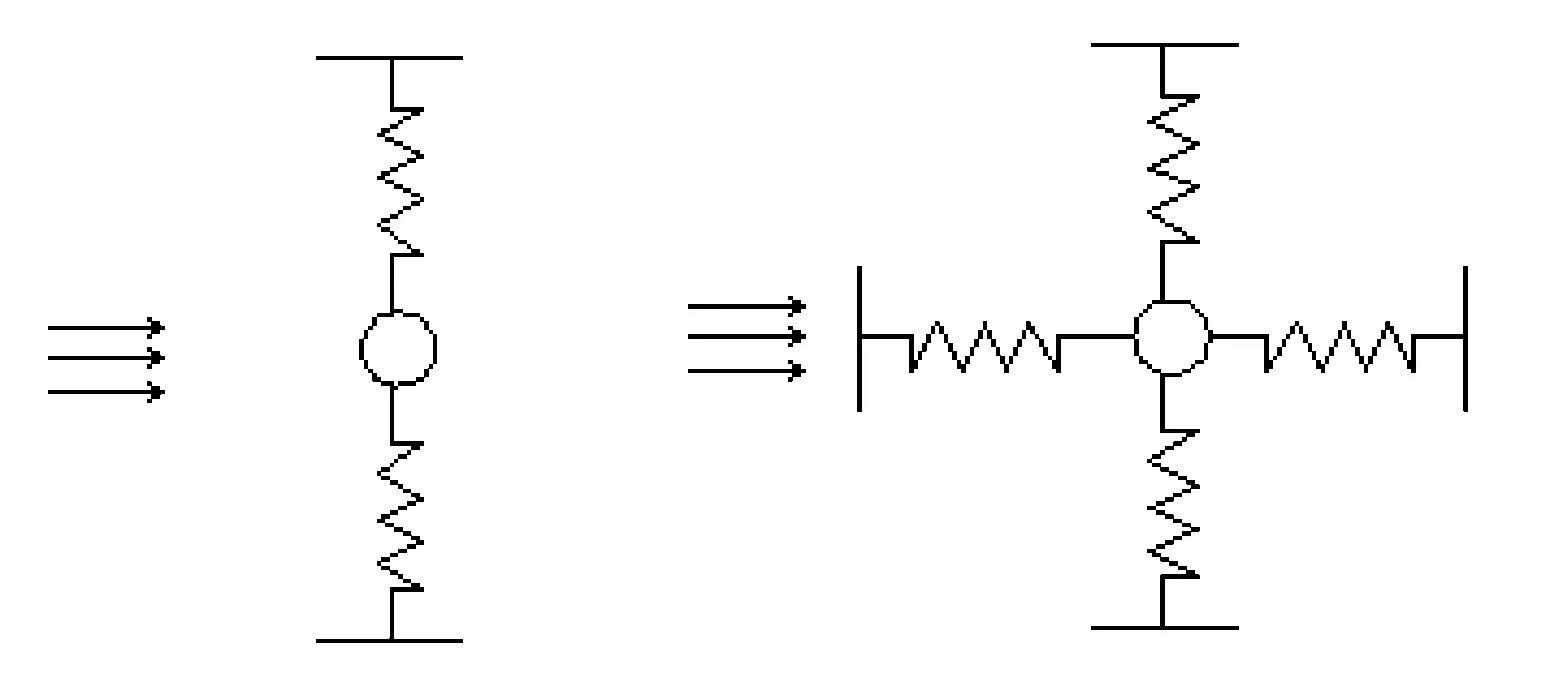
图1 涡激振动弹性系统简图
1.4 网格划分及边界条件
模型计算域及网格划分如图2所示,其中圆柱取直径取为0.02 m,计算域取50D×20D的长方形区域,高度取L=8D。设定圆柱上游区域为15D,尾流区为35D,距两侧边界各为10D。将计算域进行分块进行网格划分,因DES湍流模型对网格要求较高,因此需满足y+≈1的要求,并确定第一层网格高度。在圆柱体附近采用O型网格划分,并在靠近柱体表面处进行加密,如图2所示。这种网格划分,网格质量较高,可加快收敛,有效提高数值模拟的精确度。
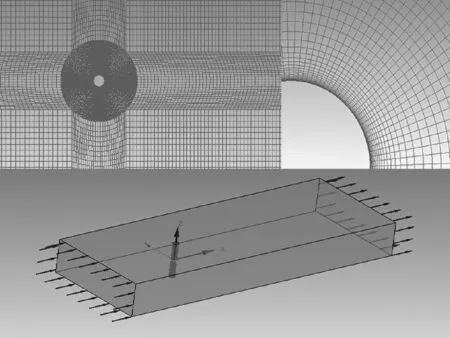
图2 计算域及网格划分
边界条件设定上,入口采用速度入口边界;出口采用自由流出边界;四周边界采用滑移壁面边界;圆柱体表面采用无滑移壁面边界。
2 数值计算结果分析
2.1 固定圆柱绕流升、阻力分析
采用DES湍流模型对Re=200的固定圆柱绕流模型进行数值模拟,得到了升阻力系数Cl、Cd随时间变化的曲线。如图3所示,最终得到阻力系数均值为1.24,升力系数幅值为0.62左右;阻力系数变化的频率恰为升力系数频率的两倍,图4为升力系数频率谱曲线,可以读取谱峰频率值,根据来流速度U=0.01 m/s,进而获得对应的St。本算例的特征数据与相关数据的对比结果详见表1,可发现其结果与表1中其他试验、数值模拟数据具有较好的一致性,由此可以说明本文所采用的湍流模型、计算方法能够较好的进行相关的数值仿真。
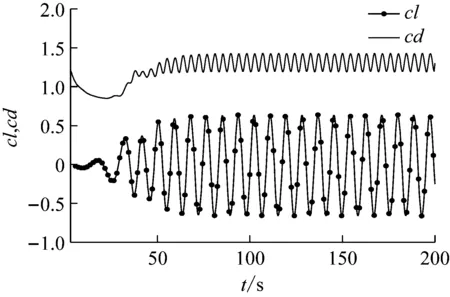
图3 Re=200时升阻力系数
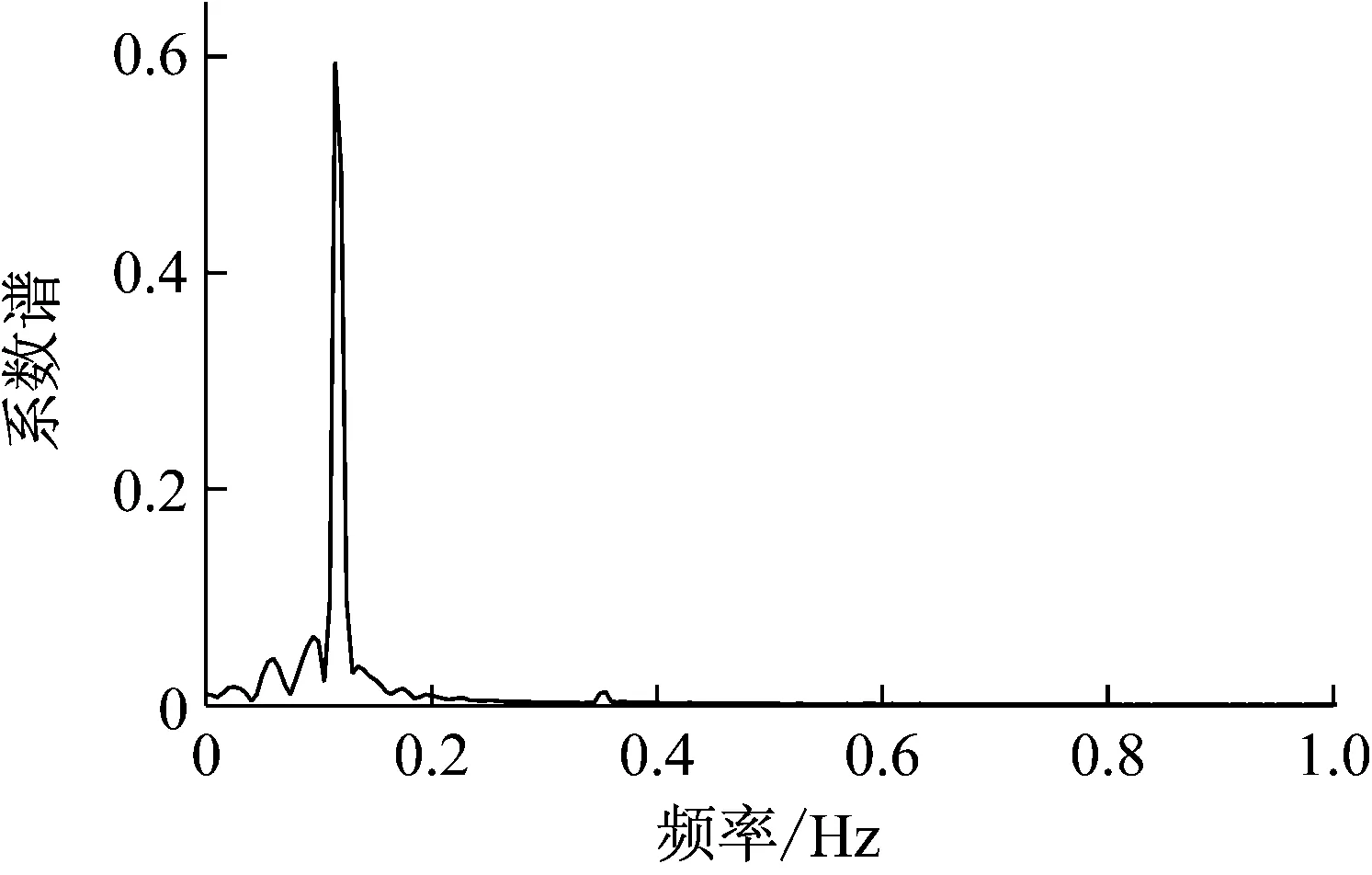
图4 升力系数谱分析图
2.2 低质量比时两自由度涡激振动
约化速度Ur是涡激振动中的重要参数,本文模拟的实际来流速度为0.1 m/s~1.0 m/s,对应的约化速度范围为1.0~10.0,对应的雷诺数范围为2×103~2×104。图5给出了质量比为1时,两自由度条件下的无因次振幅时程曲线,在较低约化速度区域内,随Ur数值增加,振幅有一定幅度增大,但幅值仍较小,还未进入锁振区;在Ur增大到3时,圆柱体开始进入大振幅振动状态;当约化速度Ur增大到8时,无因次振幅达到最大,约为1.0;之后,随Ur增大,振幅呈骤减态势。针对本计算工况,Ur=3.5~9.5的速度域,为圆柱体涡激振动的显著振动加强区,也就是所谓的锁振发生区域。图5同时显示了本文m*=1工况下的横流向无因次振幅与约化速度关系图,以及刘卓等[12]所做的m*=0.93工况下的分析结果,可以发现因两质量比非常接近,对应的两条关系曲线升、降变化趋势及锁振区间基本一致,从而进一步验证了本文所采用的数值计算方法可靠性。
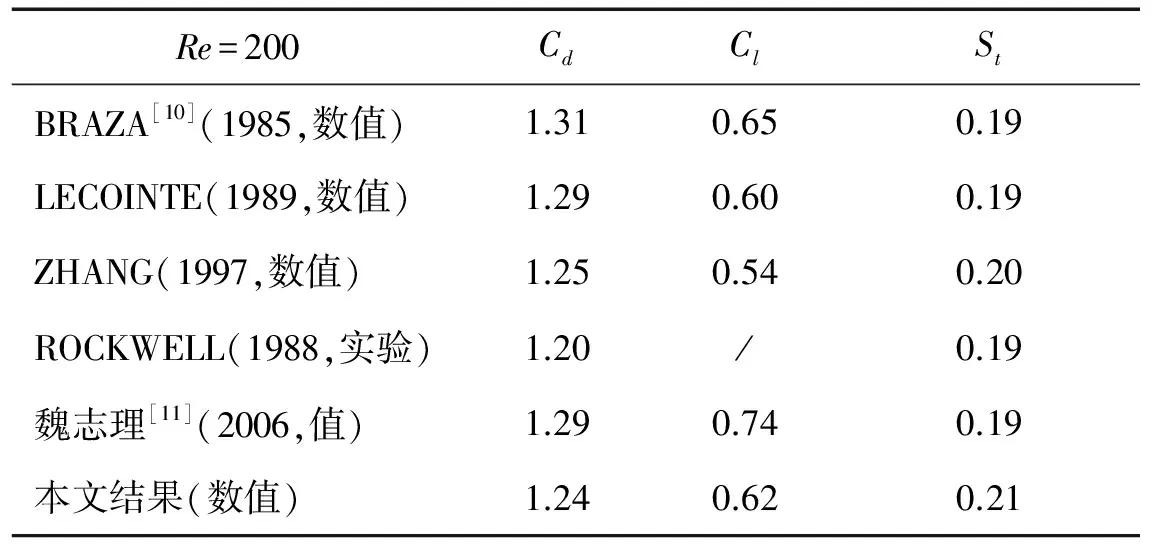
表1 Re=200时圆柱绕流国内外数据比较
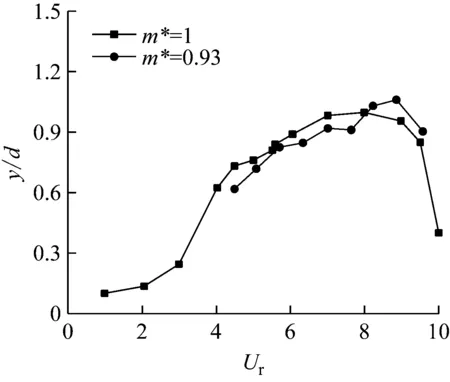
图5 横流向无因次振幅与约化速度对应关系
Fig.5 The relationship between the horizontal amplitude ratio and reduced speed
图6给出质量比为1工况下,不同约化速度对应的两自由度圆柱运动轨迹图,可以发现在稳定振动状态时,各工况下发现圆柱体的运动轨迹基本呈“8”字型。其中Ur=1~5.6的速度域,横流向振幅在增大的同时,顺流向振幅也在同步增大,而且后者的振幅增长速度要明显大于前者,因此圆柱体振动轨迹逐渐呈顺流向拉伸的趋势。特别是在Ur=1.0,2.0时,因顺流向与横流向振动间不存在相位差,因此形成的“8” 字型振动轨迹中顺流向达到最大值时,横流向也达到最大值。随着Ur增大,开始出现相位差,顺、横流向的同步现象减弱;在Ur=5.6~9的速度域,横流向振幅增速放缓,甚至在Ur>8之后逐渐缩小,同时顺流向振幅在这个区域随Ur的增加也逐步减小,使得圆柱体振动轨迹同时呈现顺流向压缩的趋势。特别是在Ur=9.0时,因存在约90°的相位差,顺、横流向振幅无法同时到达最大值。
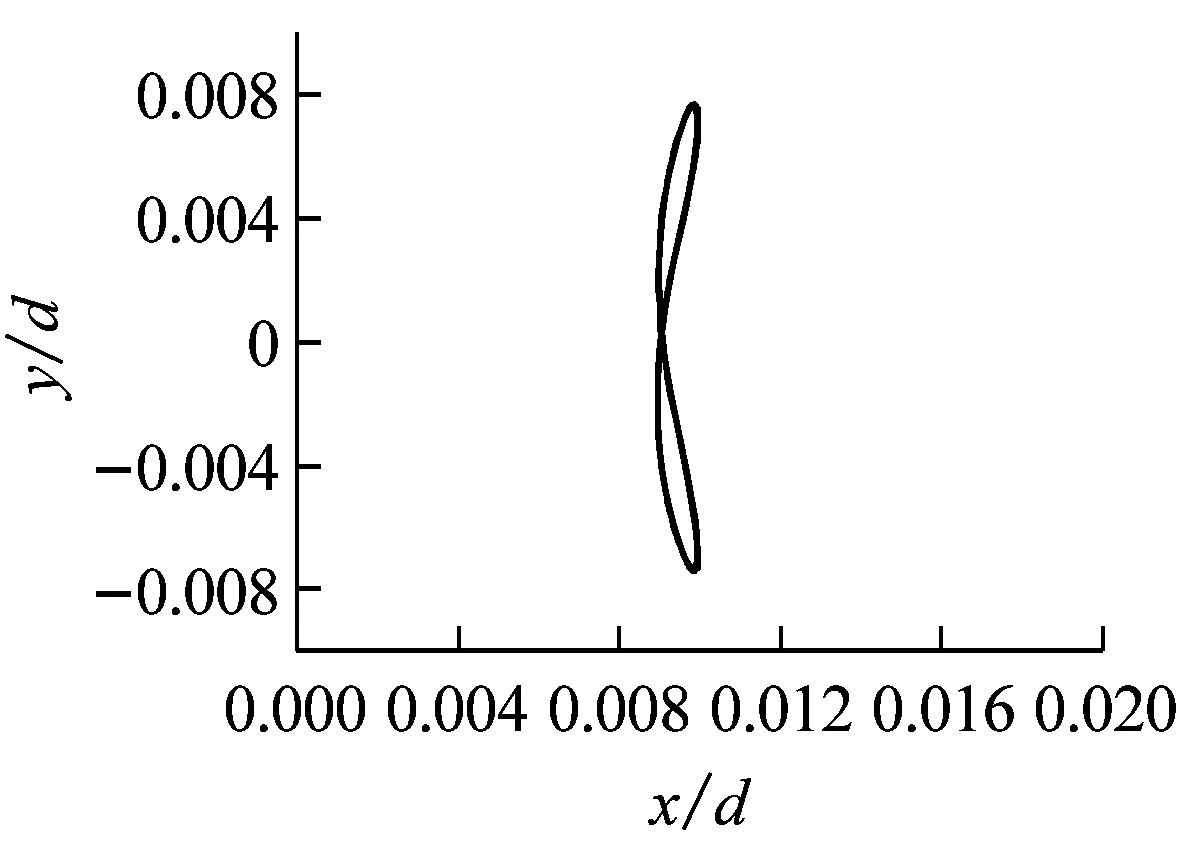
(a) Ur=1.0

(b) Ur=2.0
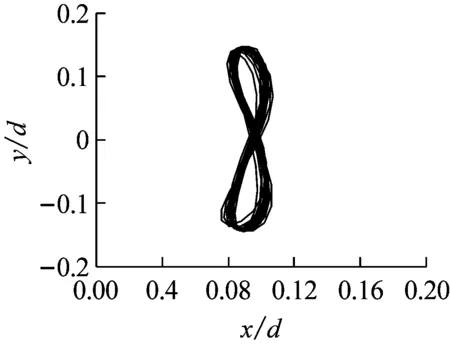
(c) Ur=3.0
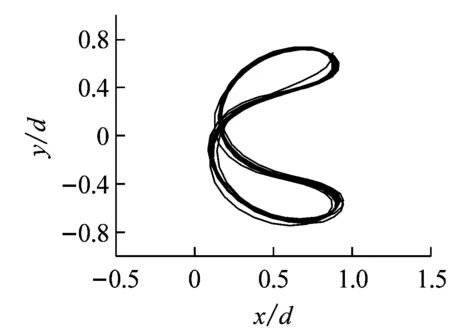
(d) Ur=5.6
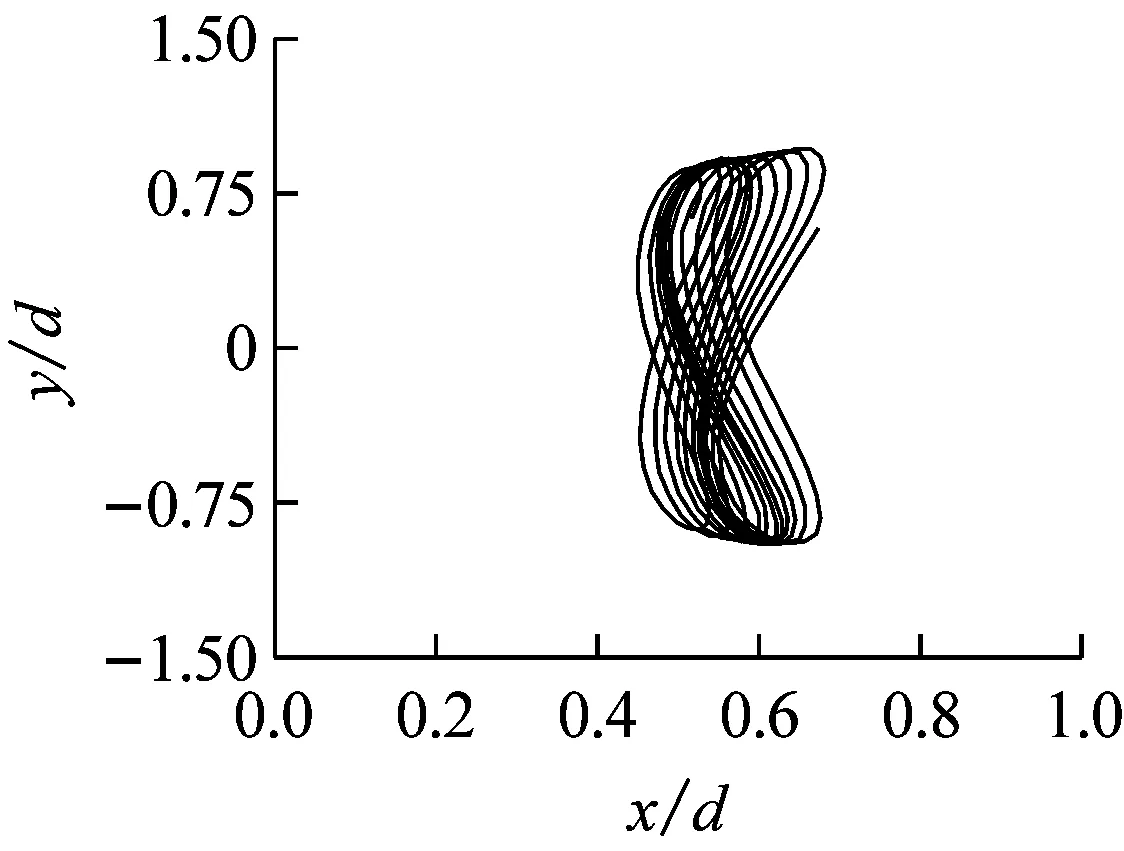
(e) Ur=8.0
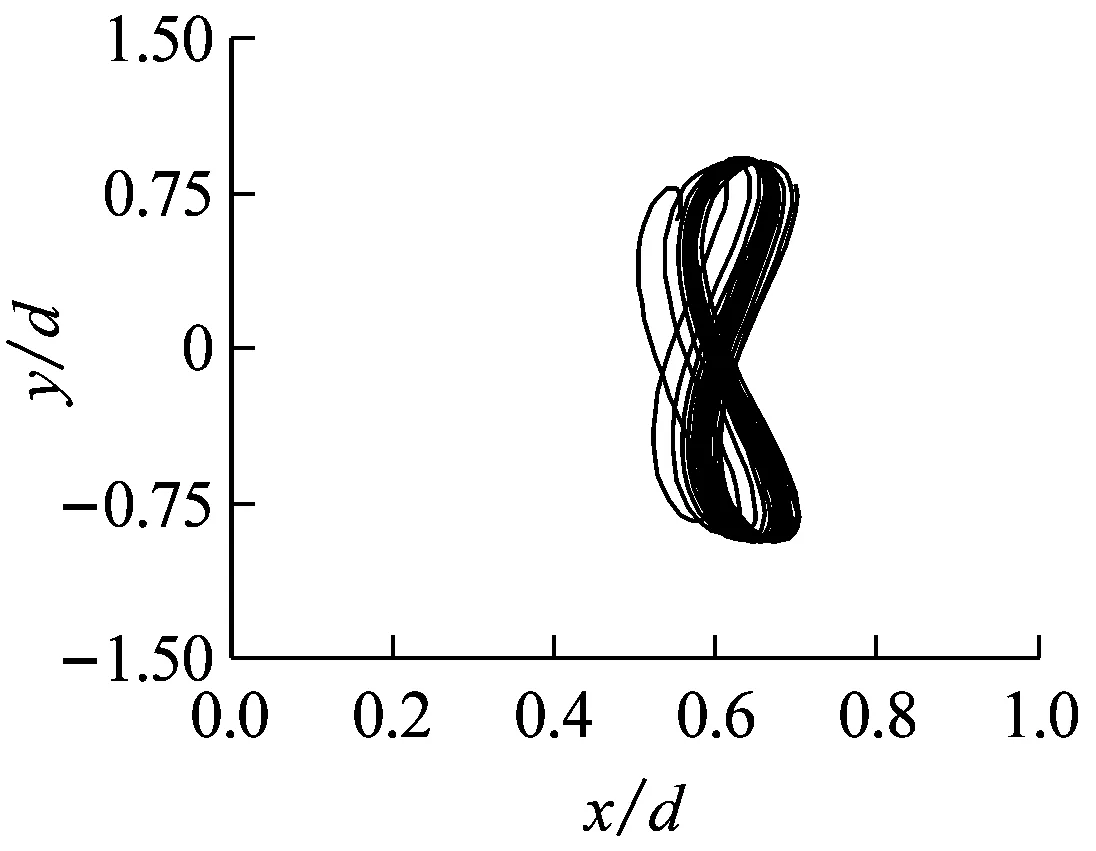
(f) Ur=9.0
本文同时模拟了m*=2.4工况下的双自由度刚性圆柱体涡激振动特性,采用与m*=1工况相同的设置条件,得到了如图7所示的振幅与约化速度之间的关系曲线。其中A线为本文数值模拟结果,B线为吴文波, 王嘉松等[13]在相同质量比及双自由度条件下的得到数值模拟结果。对比两曲线可以看出,两线整体的走势基本保持一致,但是两种数值计算工况下采用不同的湍流模型,因两者的随机扰动不同,造成了对应的曲线存在较小差异,参考文献模拟的结果在约化速度在4.8时无因次振幅达到最大值0.88左右,而本文最大无因次振幅0.83在约化速度为6附近时达到。不过,两曲线涡激振动均在约化速度为4时开始进入锁振状态,并随约化速度的增大,无因次振幅出现先增大后减小的趋势,同时也均在约化速度到达9时脱离锁振状态,从而进一步证明了本文数值模拟结果的可靠性。
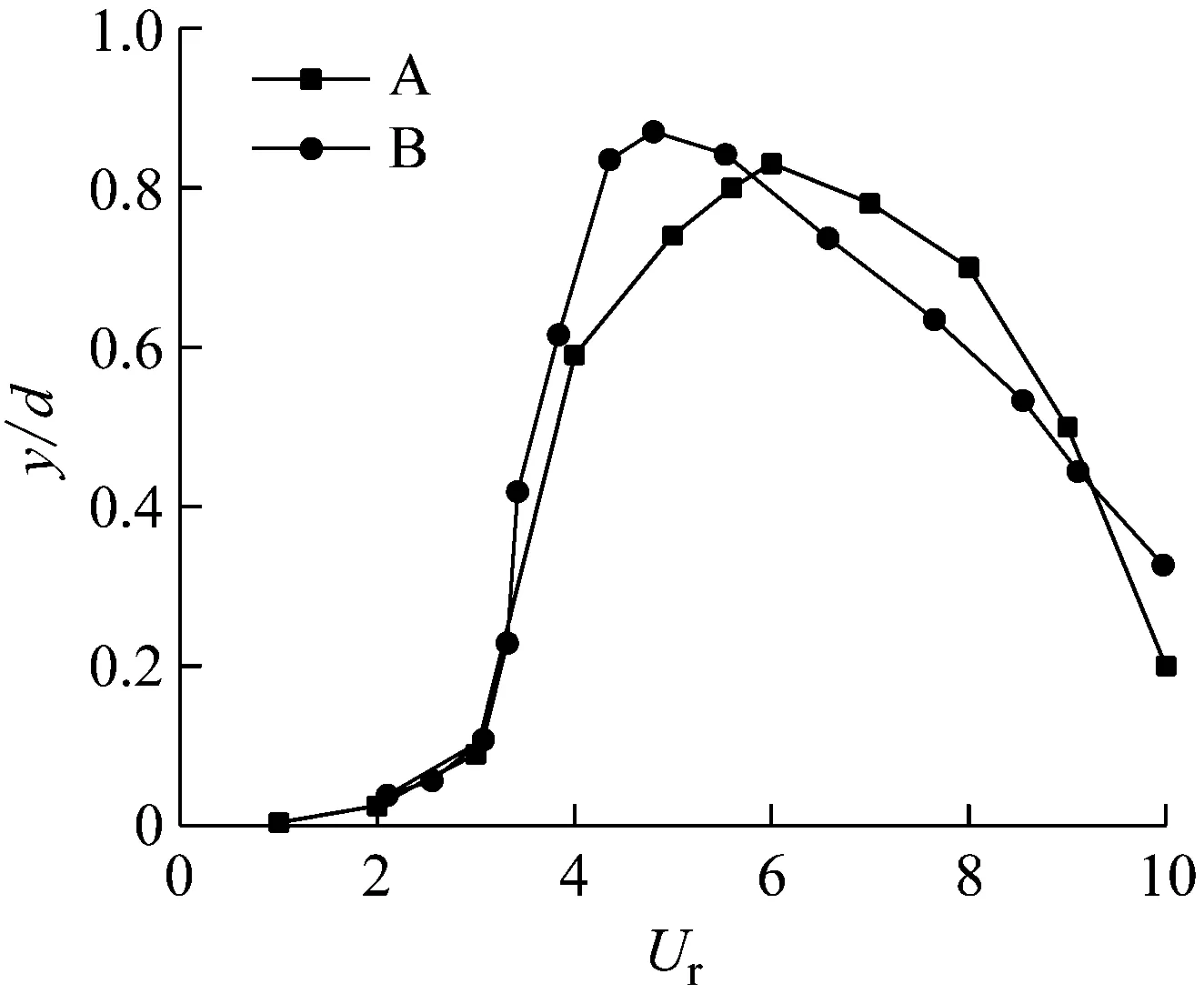
图7 m*=2.4时数值模拟结果比较
2.3 高质量比时两自由度涡激振动
设定刚性圆柱的m*=7,其他参数不变,重复与低质量比工况下相同的步骤实施数值模拟,得到了振幅与约化速度之间的关系如图8。其中A线为本文数值模拟结果,B线别为黄智勇等[14]在相同质量比条件下数值模拟的结果,观察该图可以发现,A、B两线图形变化趋势基本趋于一致,均在约化速度为4时,涡激振动变开始进入锁振区域,并均在Ur=6左右时横流向无因次振幅达到最大值,在Ur=7附近时开始减小,直至Ur=9时完全脱离锁振范围。同时可以发现A线所示横流向无因次振幅达到最大值为0.7,而B线对应值为0.6左右,存在一定差异。造成该差异的主要原因为本文中采用的是三维几何模型,对比文献中则采用的是二维几何模型,目前相当多的文献[15-16]都已经证实当雷诺数较大时,沿圆柱体延展方向的泻涡发放形态会存在三维效应,不同位置泻涡发放相位与强度不尽相同,从而造成振动强度与二维几何模型时存在差异;另外在两种模拟工况下,分别选择了不同的湍流模型,这也是造成两种数值模拟结果存在差异的原因之一。
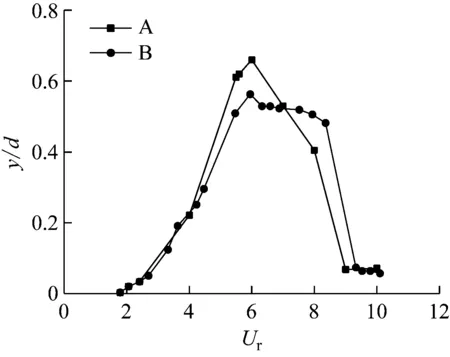
图8 m*=7时数值模拟结果比较
图9呈现了m*=7,Ur=4.0工况下,圆柱的横流向振动过程所观察到的“差拍”现象,这是涡激振动的一种重要的特征,横流向振幅随时间变化时而增大时而减小,呈较明显的群性波动特征,产生的原因是因为圆柱固有频率与涡激振动频率相近而产生的共振不稳定现象。在Ur=5.6工况下捕捉到了涡激振动中的另一种现象——“相位转换”如图10所示,图中实、虚线分别代表位移和升力系数的时程曲线,在该工况下,两者之间的相位相反,而在其他工况下,则是相同的。
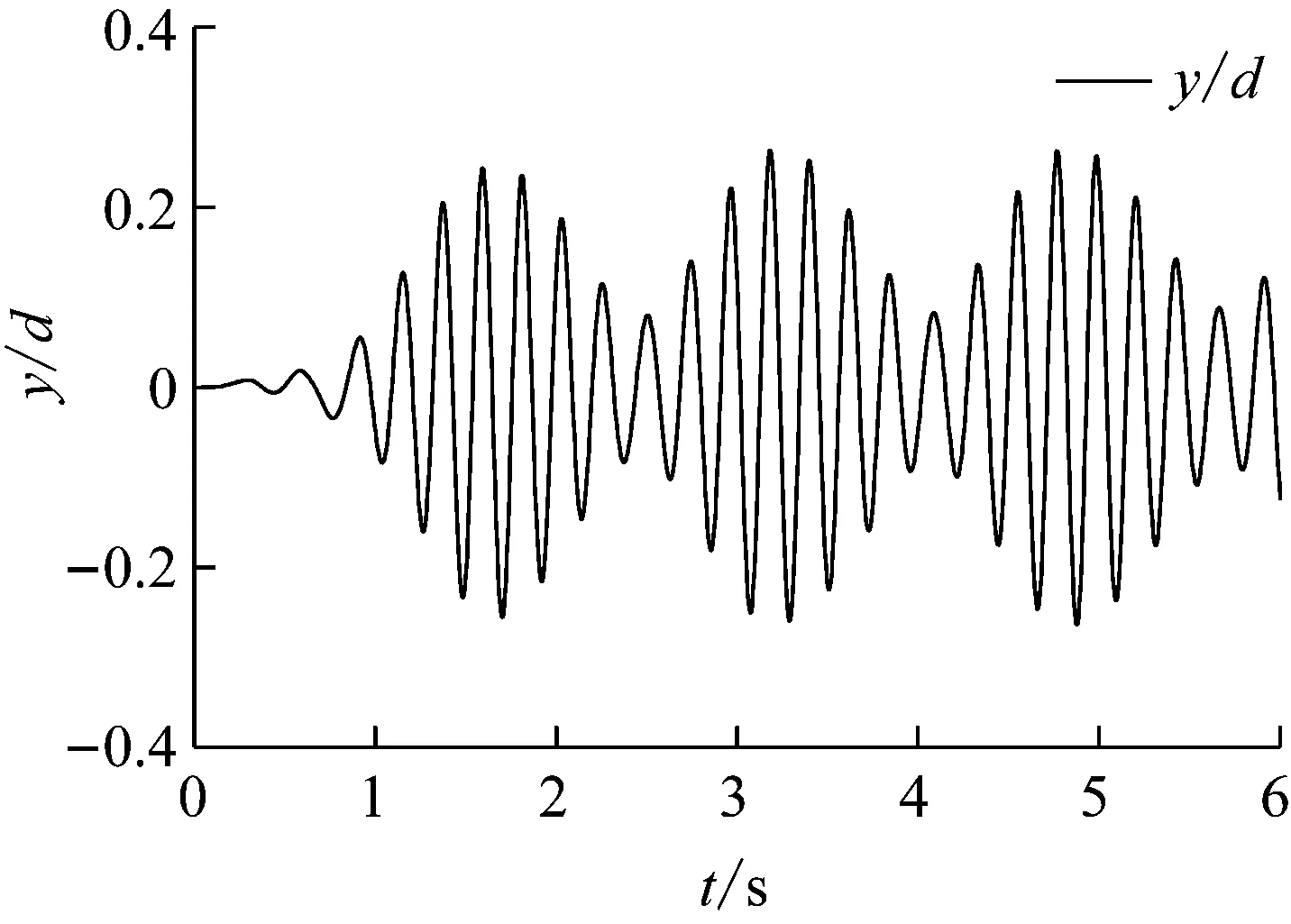
图9 “差拍”现象
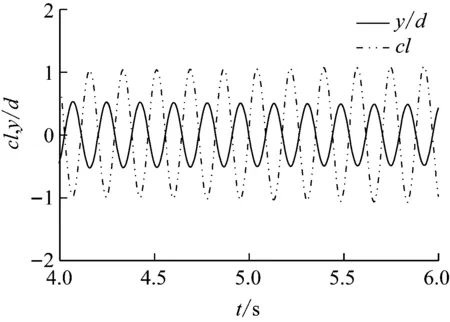
图10 相位转换现象
2.4 顺流向振动对横流向振动的影响
涡激振动是一种同时产生顺流向振动和横流向振动的过程,因此两个方向的振动形态必然存在一定程度的耦合效果。本文以质量比分别为1、2.4和7的单、双自由度刚性圆柱体为例,设定约化速度Ur=5.6,由此分析顺流向对横流向振幅产生的影响程度。图11(a)给出了质量比为1工况下的横向无因次振幅随时间变化曲线,其中实线代表双自由度,虚线代表单自由度,结果表明,在此工况下,考虑顺流向振动的双自由度模型的横流向无因次振幅最大值,比单自由度模型的对应值大15%左右。该数值要稍大于Jauvtis等[17]在类似工况下得到的无因次振幅最大值增幅为10%的推测。图11(b)给出质量比为2.4工况下,单、双自由度无因次振幅随时间变化的曲线,可以得到在此工况下,考虑横流向的无因次振幅交较不考虑时增大10%左右,此工况下,顺流向因素同样不可忽略。图11(c)给出质量比为7工况下的横流向无因次振幅随时间变化曲线,可以看出单、双自由度模型对应的涡激振动过程曲线非常接近,从而说明顺流向对横线振动过程产生的影响在此工况下并不大。
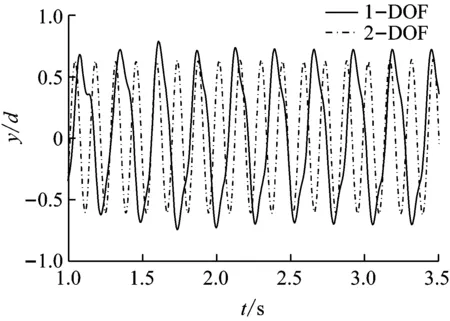
(a) m*=1时位移时程曲线
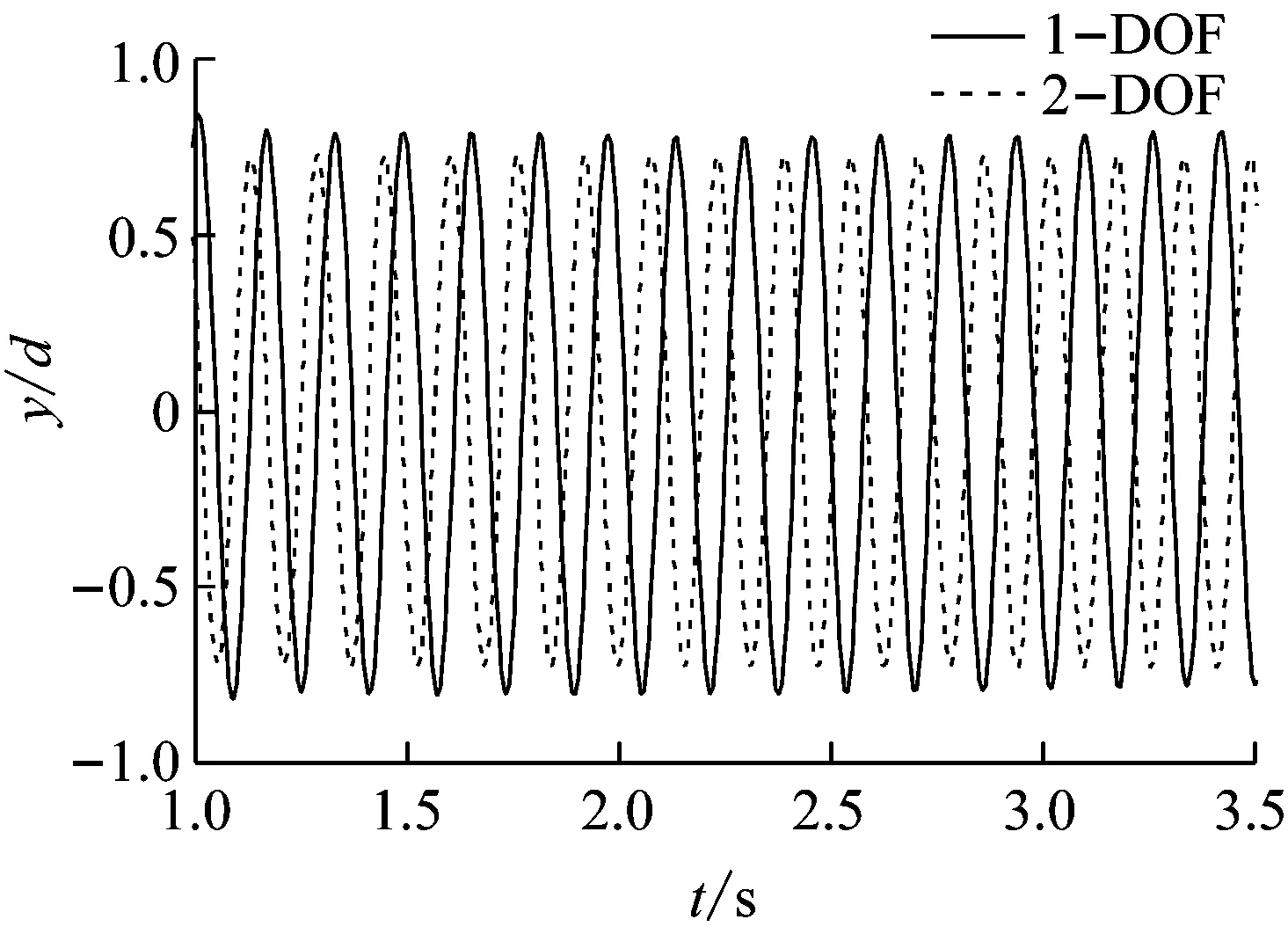
(b) m*=2.4时位移时程曲线
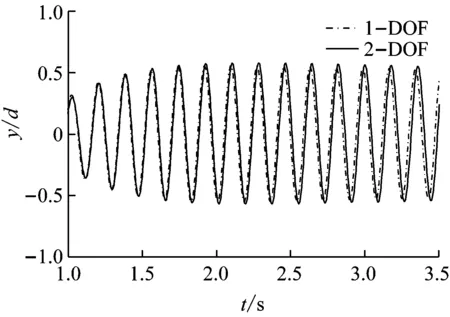
(c) m*=7时位移时程曲线
质量比对刚性圆柱体的振动特性产生了重要影响,分析认为,主要因不同质量比时,附加质量相对于圆柱体自身质量所占比例不同引起。低质量比时,附加质量所占总质量比重较大,振动的圆柱体可以根据附加质量的变换不断调节自振频率使其与泄涡频率相近,不但增大了锁振区范围,同时也增大了顺流向振动特性;高质量比时,附加质量相对圆柱体自身质量较小,对自振频率的调节性能也相对较差,从而锁振区范围及顺流向的影响也均较小。
2.5 尾流特征分析
如图12,给出了质量比为1和7工况下的泻涡发放涡量云状图。尾流区泻涡随着刚性圆柱体的振动形态呈周期性的发放,尾涡中分别捕捉到了对应于不同工况下的“2S”,“2P”型的涡型;其中(a)为静止圆柱绕流时的泻涡分布云状图,观察到为“2S”型的泻涡形态。质量比为1,约化速度较小时,在双自由度振动模型的尾涡中,观察到了“2S”型泻涡发放形态,如图(b)所示;约化速度较高时,在锁振区范围内,出现了“2P”型的泻涡发放形态,如图12(c)、(d)所示,泻涡发放频率与圆柱体振动频率完全一致,该型泻涡的出现将会使得振幅增大,共振过程更加稳定;“2P”型泻涡发放是一个典型稳定的、强周期性的过程,因此可以说一旦形成“2P”型泻涡发放形态,那么便很难被破坏[18]。质量比为7,且约化速度较高的工况下,也同时观察到了“2P”型的泻涡发放形态,如图(e)、(f)所示。可以发现,涡量的扩散区域较质量比为1时明显变窄,而所产生的泻涡状态也较低质量比时更加稳定。

(a) 静止圆柱绕流

(b) m*=1,Ur=1.0

(c) m*=1,Ur=5.6

(d) m*=1,Ur=7.0
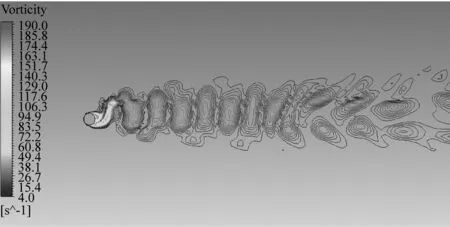
(e) m*=7,Ur=5.6

(f) m*=7,Ur=7.0
3 结 论
本文基于CFD方法与双向流固耦合数值仿真技术,开展了质量比对刚性圆柱体涡激振动影响的研究。得到了不同质量比条件下无因次化振幅与约化速度之间的变化关系、分析了质量比对单自由度模型横流向振动的影响,以及质量比对双自由度模型中顺、横流向耦合振动影响的程度。
(1) 质量比对锁振区范围及最大横流向无因次振幅的影响程度较显著。在双自由度模型中,质量比为1模型的锁振区范围为3.5~9.5,横流向最大无因次振幅约为1;质量比为2.4模型对应的锁振区范围为4~9,最大无因次振幅为0.83;质量比为7模型对应的锁振区范围为4~7,最大无因次振幅仅达到0.7。三种模型对比发现,在相同流速工况下,低质量比的刚性圆柱体不仅更容易发生锁振,而且其振动程度更为剧烈。
(2) 质量比是决定顺流向振动分量对横流向振动影响显著化的一项重要因素。对比单、双自由涡激振动模拟结果,发现在质量比为1工况下,顺流向振动会造成对应的横向振动无因次振幅增大约15%左右,质量比为2.4工况时,增大10%左右;而质量比为7工况下,顺流向振动分量对横流向振动振幅的影响可以忽略。最终研究表明越是低质量比值的工况,顺流向振动分量对整个振动形态的影响也越需要重视。
(3) 尾流区的“2P”型的泻涡发放是促使涡激振动趋于加剧化,并最终稳定的一种泻涡发放形态。因为本文所有算例中,Reynolds数相对较低,尾流区泻涡随着刚性圆柱体的振动形态均呈现出周期性的交替发放形态,尾涡中分别捕捉到了对应于不同工况下的“2S”、“2P”;一般说来锁振区以外基本为“2S”型的泻涡发放类型,在锁振区范围内,在尾流区基本呈现出“2P”型的泻涡发放类型,这种泻涡发放类型,可使得振幅增大,共振过程更加稳定。
[1] FENG C C. The measurement of vortex-induced effect in flow past a stationary and oscillating circular and D-section cylinders[D]. University of British Columbia, Vancouver, 1968.
[2] VIKESTAD K, VANDIVER J K, LARSEN C M. Added mass and oscillation frequency for a circular cylinder subjected to vortex-induced vibrations and external disturbance[J]. Journal of Fluids and Structures, 2000, 14(7): 1071-1088.
[3] SANCHIS A, SLEVIK G, GRUE J. Two-degree-of-freedom vortex-induced vibrations of a spring-mounted rigid cylinder with low mass ratio[J]. Journal of Fluids and Structures, 2008, 24: 907-919.
[4] KHALAK A, WILLIAMSON C H K.Dynamics of a hydroelastic cylinder with very low mass and damping[J].Journal and Fluids and Structures,1996, 10:455 -472.
[5] 曹淑刚,黄维平,顾恩凯.考虑流固耦合的弹性圆柱体涡激振动研究[J]. 振动与冲击,2015, 34(1): 58-62.
CAO Shugang, HUANG Weiping, GU Enkai.Vortex-induced vibration of an elastic cylinder considering fluid-structure interaction[J]. Journal of Vibration and Shock, 2015, 34 (1):58-62.
[6] 常书平,王永生,庞之洋.用基于SST模型的DES方法数值模拟圆柱绕流[J]. 舰船科学技术, 2009, 31(2): 30-33.
CHANG Shuping, WANG Yongsheng, PANG Zhiyang. Numerical simulation of flow around circular cylinder using SST DES mode[J]. Ship Science and Technology, 2009, 31(2): 30-33.
[7] 薛帮猛,杨永.基于两方程湍流模型的DES方法在超音速圆柱底部流动计算中的应用[J]. 西北工业大学学报, 2006, 24(5):544-547.
XUE Bangmeng, YANG Yong. Technical details in applying DES method to computing supersonic cylinder-Base Flow[J]. Journal of North Western Polytechnical University, 2006, 24(5): 544-547.
[8] STRELETS M. Detached eddy simulation of massively separated flows[R]. AIAA-01-0879, 2001.
[9] 潘志远. 海洋立管涡激振动机理与预报方法研究[D]. 上海: 上海交通大学, 2005.
[10] BRAZA M, CHASSAING P, HA MINH H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J]. Journal of Fluid Mechanics, 1986, 165: 79-130.
[11] 魏志理,孙德军,尹协远. 圆柱尾迹流场中横向振荡翼型绕流的数值模拟[J]. 水动力学研究与进展(A辑), 2006, 21(3):299-308.
WEI Zhili, SUN Dejun,YIN Xieyuan. A numerical simulation of flow around a transversely oscillating hydrofoil in the wake of a circular cylinder[J]. Chinese Journal of Hydrodynamics, 2006, 21(3): 299-308.
[12] 刘卓, 刘昉, 燕翔,等.高阻尼比低质量比圆柱涡激振动试验研究[J].实验力学,2014, 29(6): 737-743.
LIU Zhuo, LIU Fang, YAN Xiang, et al. Experimental Study of Cylinder vortex induced vibration under high damping ration and low mass ration condition[J]. Journal of Experiment Mechanics, 2014, 29(6): 737-743.
[13] 吴文波,王嘉松.基于OpenFOAM的圆柱涡激振动数值模拟研究[C]∥中国海洋工程学会.第十六届中国海洋(岸)工程学术讨论会论文集.北京:海洋出版社,2013,147-151.
[14] 黄智勇,潘志远,崔维成.两向自由度低质量比圆柱体涡激振动的数值计算[J]. 船舶力学, 2007, 11(1):1-9.
HUANG Zhiyong, PAN Zhiyuan, CUI Weicheng. Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio[J]. Journal of Ship Mechanics, 2007, 11(1):1-9.
[15] 王亚玲,刘应中,缪国平.圆柱绕流的三维数值模拟[J]. 上海交通大学学报, 2001, 35(10): 1464-1469.
WANG Yaling, LIU Yingzhong, MIAO Guoping. Three-dimensional numerical simulation of viscous flow around circular cylinder[J]. Journal of Shang Hai Jiao Tong University, 2001, 35(10): 1464-1469.
[16] 姚熊亮,方媛媛,戴绍仕,等.基于LES方法圆柱绕流三维数值模拟[J].水动力学研究与进展(A辑),2007,22(5):564-571.
YAO Xiongliang, FANG Yuanyuan,DAI Shaoshi,et al. Three-dimensional numerical simulation of the flow past a circular cylinder based on LES method[J]. Chinese Journal of Hydrodynamics, 2007,22(5):564-571.
[17] JAUVTIS N, WILLIAMSON C H K. Vortex-induced vibration of a cylinder with two degrees of freedom[J]. Journal of Fluids and Structures, 2003, 17: 1035-1042.
[18] 陈正寿. 柔性管涡激振动的模型实验及数值模拟研究[D]. 青岛:中国海洋大学, 2009.
Effects of mass ratio on vortex-induced vibration of a rigid cylinder
CHEN Zhengshou1,2, ZHAO Zongwen1, ZHANG Guohui1, ZHENG Wu3, YAN Shenghan4
(1. School of Naval Architecture and Mechanical-electrical Engineering, Zhejiang Ocean University, Zhoushan 316022, China; 2. Key Laboratory of Offshore Engineering Technology, Zhoushan 316022, China; 3. The Paxocean Engineering Co, Ltd, Zhoushan 316057, China; 4. Zhejiang Ouhua Shipbuilding Co, Ltd, Zhoushan 316101, China)
Based on the CFD method, the effects of mass ratio on vortex-induced vibration (VIV) of a rigid cylinder were studied. Numerical simulations for 2-DOF vortex-induced fluid-structure coupled vibration of a rigid cylinder with mass ratios of 1, 2.4 and 7 were performed. The correlations between normalized vibration amplitude and reduced velocity, 8 shape trajectories, beats and phase switch phenomena were obtained under different mass ratios. The preliminary study showed that the vibration ‘lock-in’ region for lower mass ratios is larger than that for the higher mass ratio, the cross-flow maximum normalized amplitude for the former is also larger, VIV phenomenon for the former is more obvious; the effect of the down-stream vibration on the cross-flow vibration can’t be ignored when the mass ratio is 1 and 2.4, but this effect is very small when the mass ratio is 7; ‘2S’ and ‘2P’ vortex shedding modes appear in the wake of VIV.
mass ratio; vortex-induced vibration; fluid-structure interaction; rigid cylinder
国家自然科学基金(41476078);浙江省公益技术应用研究计划项目(2015C34013);舟山科技计划项目(2014C41003)
2015-10-14 修改稿收到日期:2016-04-09
陈正寿 男,教授,1979年生 E-mail:aaaczs@163.com
P751
A
10.13465/j.cnki.jvs.2017.11.038
