双激振模式下的压实系统整体动力学分析与试验
2017-06-19沈培辉林述温
沈培辉, 林述温
(1.福建船政交通职业学院,福州 350007; 2.福州大学 机械工程及自动化学院,福州 350002)
双激振模式下的压实系统整体动力学分析与试验
沈培辉1, 林述温2
(1.福建船政交通职业学院,福州 350007; 2.福州大学 机械工程及自动化学院,福州 350002)
双钢轮振动压路机在双激振模式下,存在特有的振动特性,综合考虑不同压实阶段土壤物料的非对称滞回特性和前后轮可能跳振脱耦的实际工况,提出7自由度整体动力学模型,一次近似下,采用谐波线性化和Krylov Bogolyubov Mitropolsky(KBM)相结合的方法获得不同压实阶段的等效刚度和阻尼,并系统研究驾驶室由于前后轮振动频率差引起的拍振运动特性,在不同的压实工况模型参数下,庞加莱运动截面体现出单周期,双周期分叉,三周期直至多周期的非线性运动特性;压实中后期,系统产生高次超谐波共振和亚谐波共振,在大的激振力和低频作业下,驾驶室拍振运动进入混沌振动,通过合理调整激振力和双激振频率,可以有效地抑制混沌,从而延长压路机零部件的使用寿命和提高操作舒适性,现场的施工压实试验验证了提出模型和理论分析的合理性。
压实系统;动力学模型;拍振;脱耦;混沌
振动压路机在建筑机械、交通运输等基础行业中扮演着重要的角色,双激振钢轮振动压路机因其具有碾压平整和压实效率高等特别之处,在沥青路面施工和机场跑道等密实工程中得到广泛地应用[1-3]。压实机械的发展与压实技术的革新离不开压实机理动力学模型的研究,Yoo等[4]首先提出二自由度集中质量线性模型,Grabe[5]根据压实土壤初期能量耗散机理提出滞回模型,Anderegg[6]针对压实中后期振动轮可能跳离材料面层提出跳振模型,Beainy等[7]根据物料的塑性变形本质提出黏弹性跳振模型,Kenneally等[8]指出土壤压实全过程滞回模型的慢变特性。然而,以上研究主要针对单钢轮压路机或是双钢轮压路机的单轮简化研究。而双钢轮振动压路机行进压实过程中,其整体动力学特性较单钢轮复杂,前后振动轮的在双激振相互耦合拍振等现象在单钢轮模型中未能得到很好地解释。
为使压实机械和压实技术的进一步发展,本文综合考虑双钢轮压路机作业过程中的跳振脱耦和滞回特性,整体分析驾驶室的拍振响应,并通过现场的试验数据证明,在保证作业质量的情况下,合理选择施工工艺参数可以弱化压实系统的拍振非线性运动。
1 双激振整体动力学模型的建立
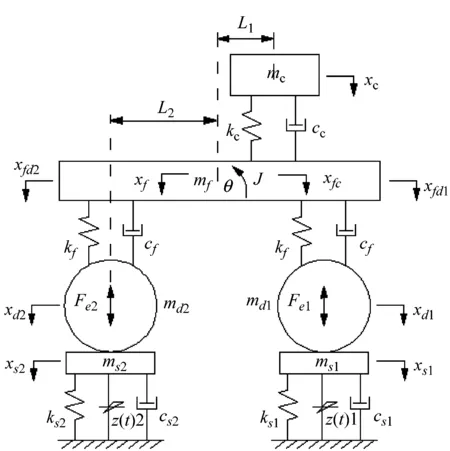
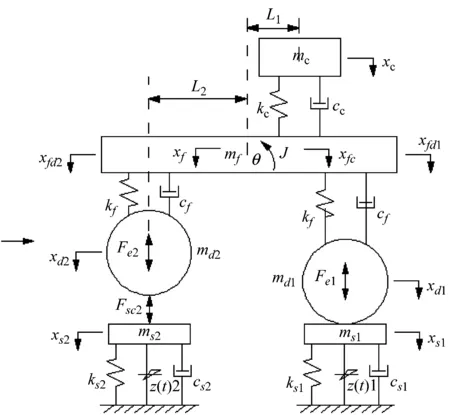
综合双钢轮振动压路机的结构特点和工作特性,以福州大学和厦工三重合作生产的YZC12试验样机为分析案例,建立如图1所示的7自由度振动压路机-压实物料整体动力学模型。
(a) 接触工况
(b) 跳振脱耦工况
图1模型中,充分考虑双钢轮压路机实际压实过程中,前后钢轮可能存在跳离压实物料面层和土体本身存在的密实迟滞能耗非线性特性,行进工况中,前后轮的物料本征也存在差异。同时,系统连耦、前轮跳振脱耦、后轮跳振脱耦和前后轮同时跳振脱耦的施工工况相互转换由图2说明,以ks1、ks2和cs1、cs2分别表示前后轮压实土壤物料的线性刚度和阻尼系数。假设前后振动轮的一级减振块基本对称,忽略其间隙等非线性因素,以kf和cf线性刚度和阻尼来简化,同理以线性刚度和阻尼kc和cc来简化机架与驾驶室之间的二级减振系统参数。当忽略随振土质量时,图1的7自由度退化为5自由度系统,动力学方程如下:
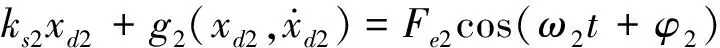
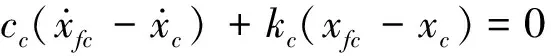
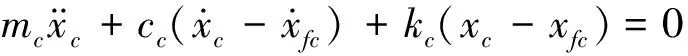
一直以来家庭都是我国老年人养老的责任主体和供给主体。新中国成立后,在倡导家庭照顾为主的基础上,国家推行的养老政策实际上具有社会福利和社会救助的双重特点,因而大多数社会老年人都不在国家责任的范围内。随着计划经济的终结,企业员工的养老问题被推向社会,而同时传统家庭养老模式开始弱化,政府自身无法面对汹涌而来的养老服务需求,于是国家开始着手社会福利改革,主要内容是推进福利机构的社会化[3]。总体来看,此阶段把解决老龄问题的视角由家庭逐步转向社会,这在方向上是正确的。但在没有形成市场、社会有效供给的局面时就过早地让渡、弱化了政府养老服务责任,收缩了福利能力,减少了部分养老福利的供给[6]。
(1)

图2 各工况的相互转换
同时存在几何关系:
(2)
考虑滞回环的参数慢变,滞回恢复力分三个代表性工况:压实初期、压实中期和压实后期,由图3所示。滞回环面积代表系统的能量耗散,即土壤物料密实时吸收的振动能量。一个周期内,振动轮位移小于物料前一个周期尚未变形的位移xe1时,认为没有压实或跳振工况,即D~E~D段;振动轮接触土壤时,近似首先进入线弹性变形D~A段,达到材料屈服极限后塑性变形A~B段,认为这个阶段材料瞬时散失抵抗力,继续加载至材料周期内不再形变的运动极限点后返回,这时分三种代表性工况分析,压实后期,非对称滞回环主要体现为超过系统0点的半空间密实,即B~O~D段;压实中期体现为全周期密实,即B~D段;而压实初期,行进过程后,物料的压实状态是非完全密实,近似认为回弹刚度系数不变,即B~C段,超过极限位置D时直接过度,或跳振,或进入下一个循环周期(在文献[4]中有提及,但尚未深入研究)。由于理论分析与现场试验均为行进工况,可忽略材料塑性变形的记忆,认为滞回环是封闭的。(注:图3中滞回模型考虑参数慢变,即压实初期的回弹刚度系数ks1小于压实后期的k″s1系数,而并非图中不变的几何关系ks1>k″s1,压实中期的分析亦然。)
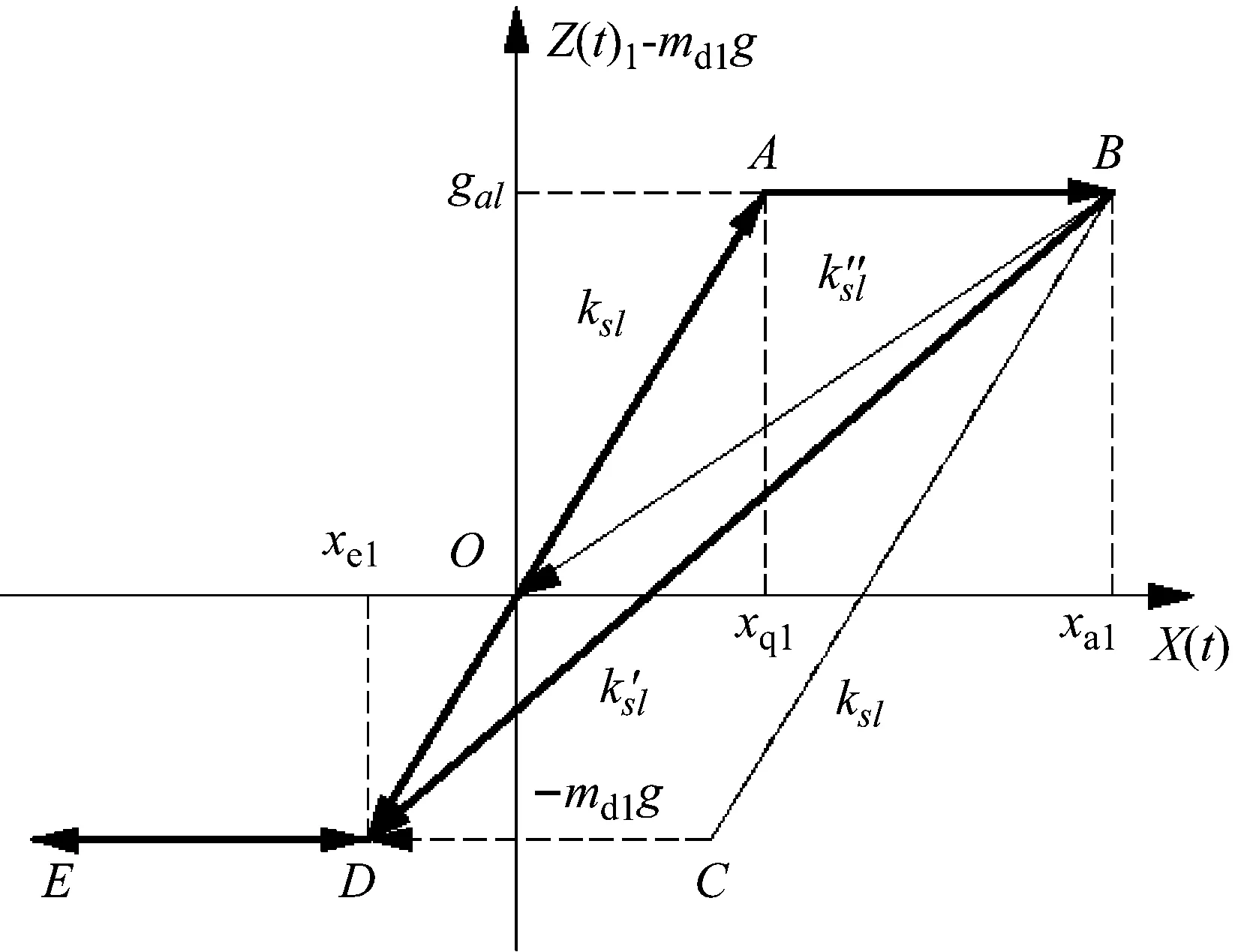
图3 各压实阶段的非对称滞回模型
Fig.3 The asymmetric hysteresis model of three compaction stages
分析图3,以前振动轮为分析对象,行进作业过程中压实土壤物料对振动轮的反作用力Fsc1表示为
(3)
其中,相对跳振,接触连耦阶段滞回模型的弱非线性特性可由Krylov-Bogolyubov-Mitropolsky(KBM)和Harmonic Balance(HB)相结合的方法推导,在一次近似下滞回力项可分阶段表示为
(4)
式中:等效刚度和阻尼系数为
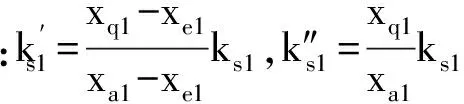
同理可获得后轮压实物料滞回恢复力的压实初期、中期和后期代表性压实阶段的等效刚度和阻尼系数为
(8)
2 压实系统动力特性理论仿真分析
以校企合作生产的YZC12型串联式振动压路机为试验样机,实测机架质心与几何中心距相比机架长度为微量级,即认为在动力学系统中重合,已知md1=md2=3 000 kg,mf=5 750 kg,mc=550 kg,L1=0.53 m,L2=1.64 m,选取kf=1.7×105N/m,cf=1.1×103Ns/m,kc=1.2×104N/m,cc=0.8×102Ns/m。
同时参考文献[15-18],选取具有代表性压实阶段的模型参数:压实初期线性刚度和阻尼系数为ks1=2.2 MN/m,cs1=70 kNs/m;压实中期取ks1=6.3 MN/m,cs1=38 kNs/m;压实后期为ks1=11 MN/m,cs1=9 kNs/m;由式(4)~(7)可计算获得前振动轮的压实迟滞物料的等效刚度和阻尼。引入后前轮压实物料线性刚度系数比β,根据压实时初期采用慢速2~3 km/h、中期复压行驶速度5~6 km/h和后期快速8~9 km/h的施工规范,和车身两钢轮接触土壤间距约为3.28 m,按照6遍施工完毕和激振偏心块使用较低频率(25~50 Hz),估算后轮土壤线性刚度系数和前轮刚度系数比β初期=1.85、β中期=1.6和β后期=1.3,由式(8)~(10)可计算获得后振动轮的压实迟滞物料的等效刚度和阻尼。
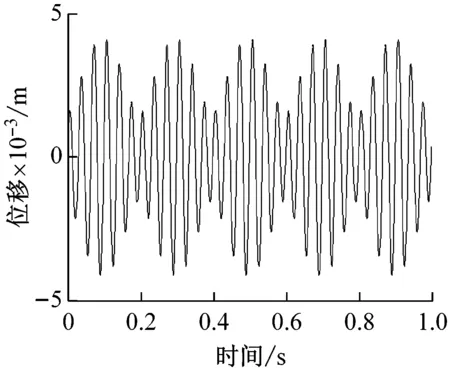
(a) 时域图
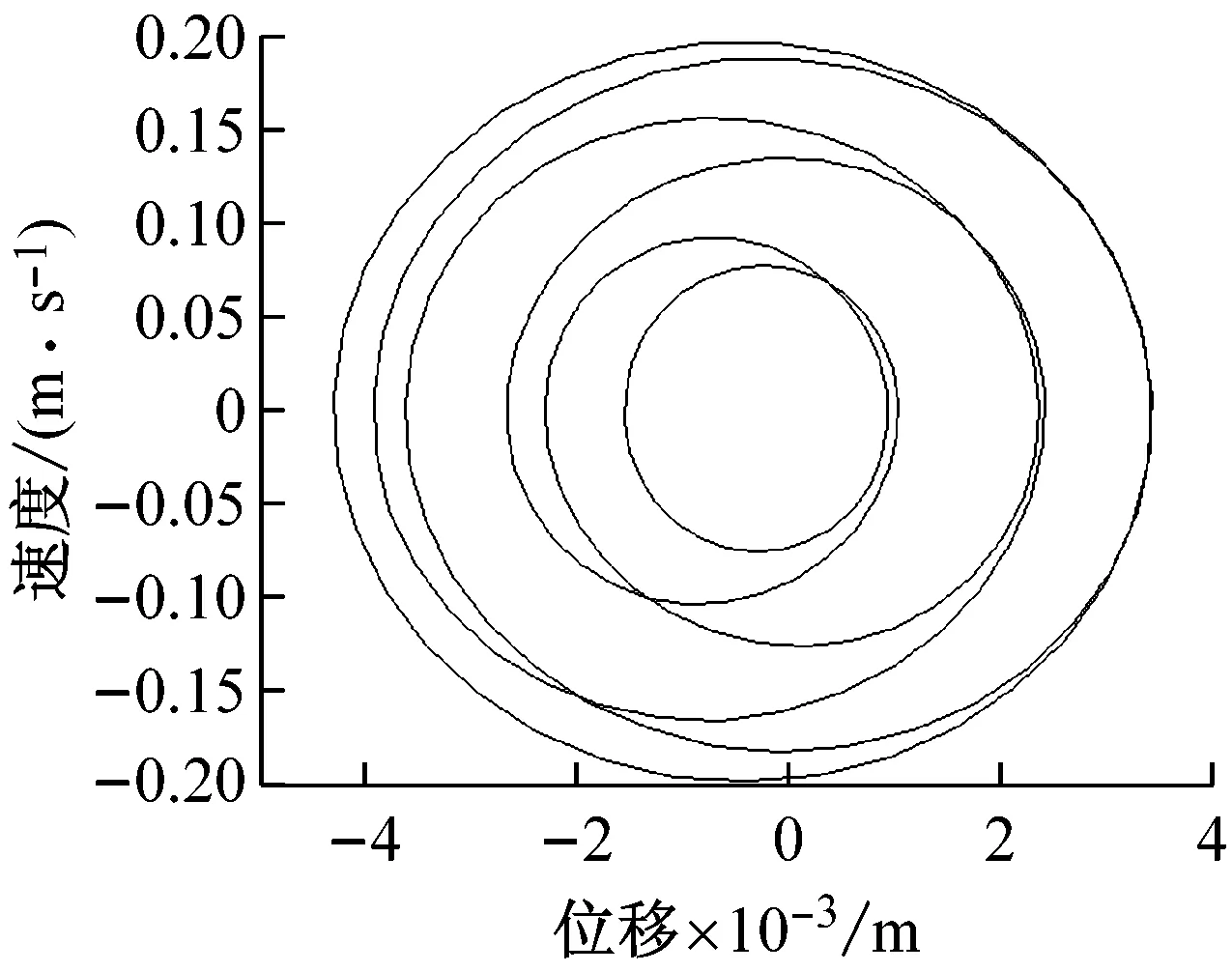
(b) 相图

(c) 拍频截面
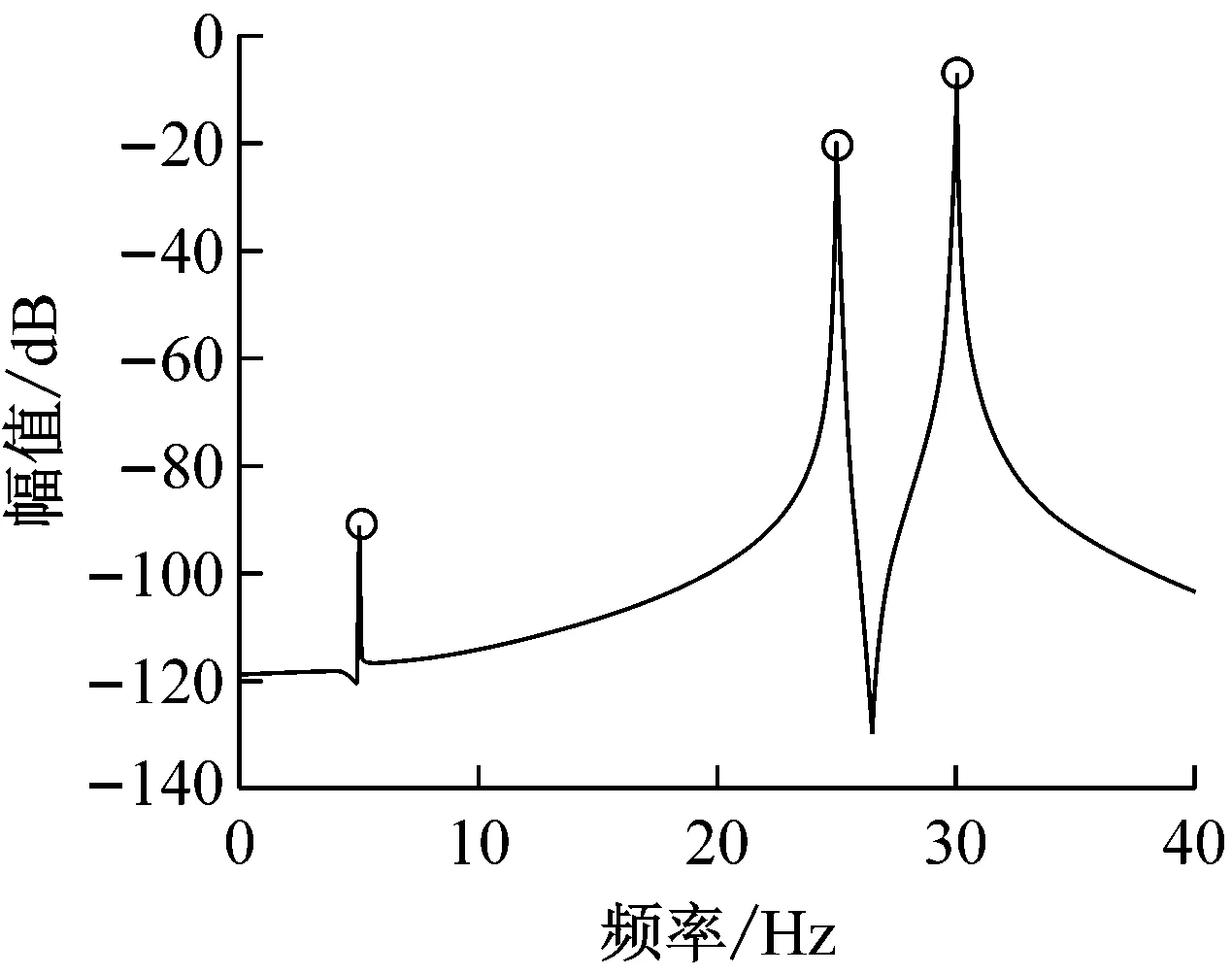
(d) 频域图
(e) 30 Hz截面
(f) 25 Hz截面
随着压实阶段进入中期,较疏松的土壤逐渐得到密实,图5为压实中期参数的模拟效果图,图5(a)的相图在图4(b)的基础上开始分叉,振动轮在物料面层上存在周期内跳振现象,图5(b)的庞加莱截面出现3周期,图5(c)的频谱响应也出现以拍振基频(30-25=5 Hz)为主的含1/3及其高次的亚谐波成分,而双激振频率成分25 Hz与30 Hz仍然是系统能量的主导。
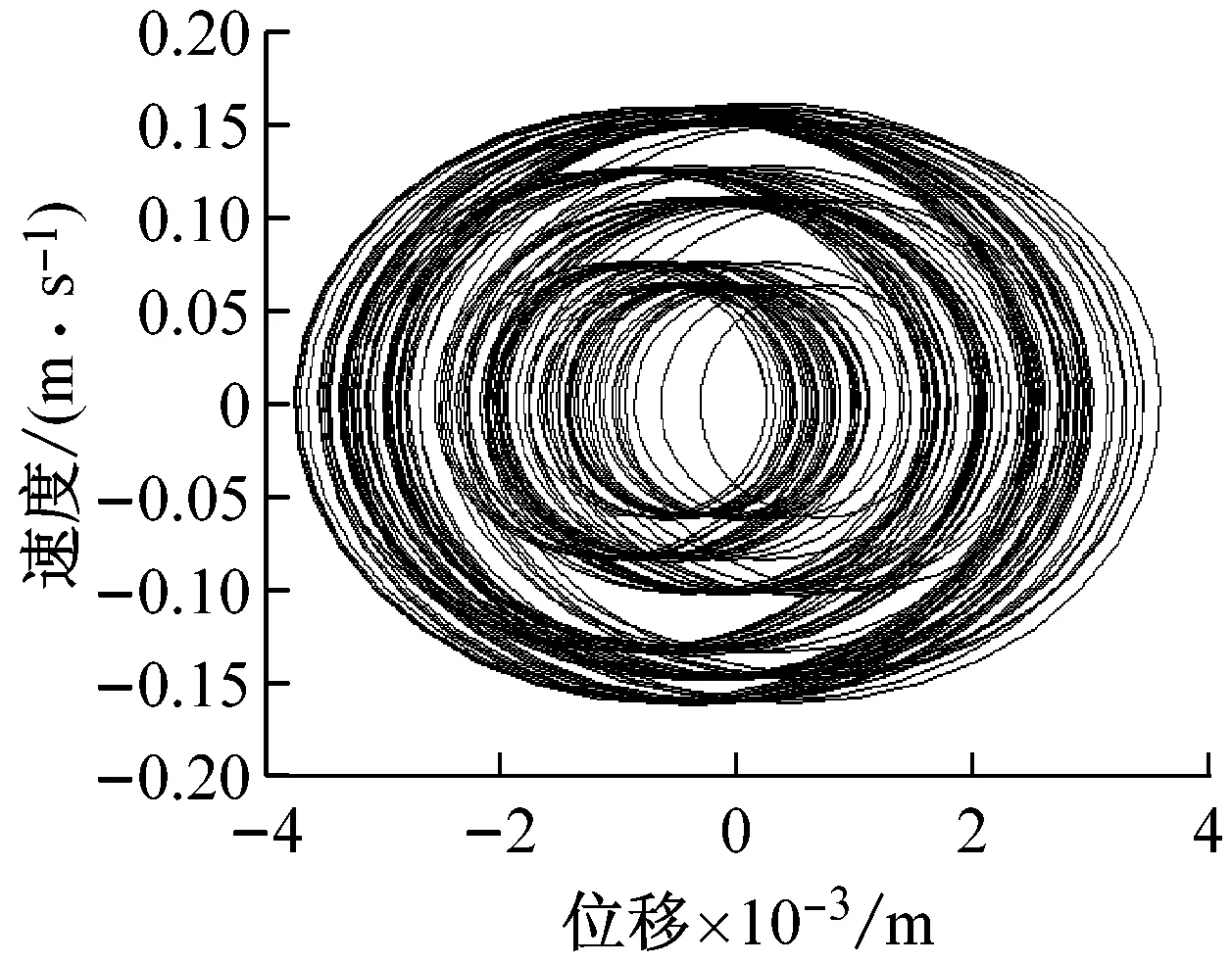
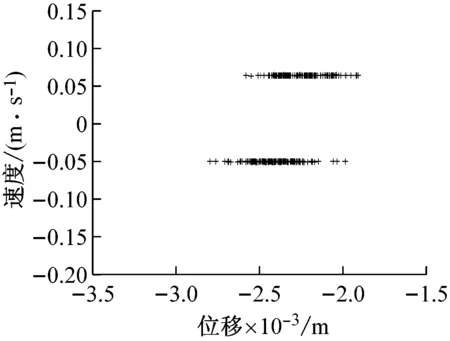
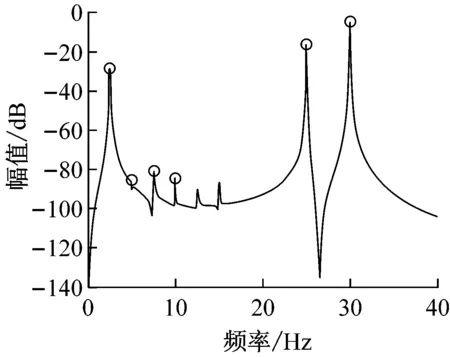
图6为采用压实后期土壤参数模型和大激振力低频双激振的模拟效果图,从图6(a)发现相平面形成奇怪的吸引子使得相图成可爱的“笑脸”灯笼状,图6(b)的驾驶室拍振界面体现出无规律映射特征,意味着系统进入混沌振动状态,图6(c)的频率特性也成近连续谱,双激振周期和拍频成分已开始模糊紊乱,可见在压实后期,物料吸收能量的承载力下降,大的激振力和低频作用下使得前后振动轮在物料面层上激烈跳振并相互耦合干涉,驾驶室开始混沌运动。
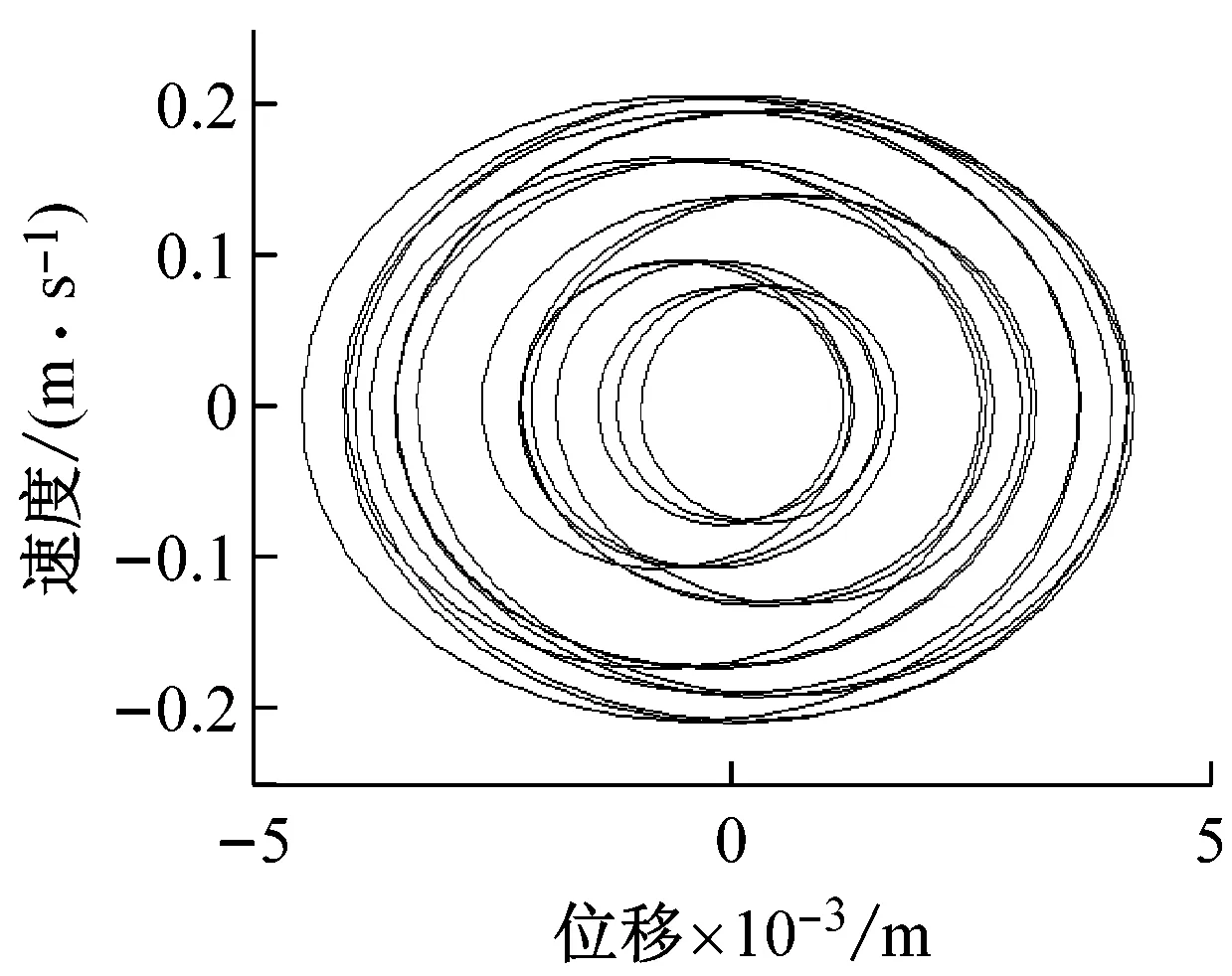
(a) 相图
(b) 庞加莱
(c) 频域图

(a) 相图
(b) 庞加莱
(c) 频域图
为弱化双激振轮的激烈跳振运动,避免驾驶室的混沌振动,在保证土壤压实质量的前提下,参考文献[19-21]研究成果中所采用的合理振频和振幅范围,压实后期首先采用小激振力(82 kN)改善模拟,如图7所示。由图7(a)的相图仍可以观察到明显的分岔现象,说明系统的非线性特性还是很强烈,图7(b)的庞加莱截面也可发现2周期分岔,图7(c)的频谱响应存在强烈的1/2拍频及其高次的亚谐波成分,同时含有丰富的2、3倍等高次谐波成分,双激振频率25 Hz与30 Hz由原来的连续谱获得明显的改善,但拍振频率成分5 Hz能量还是很弱。
(a) 相图
(b) 庞加莱
(c) 频域图
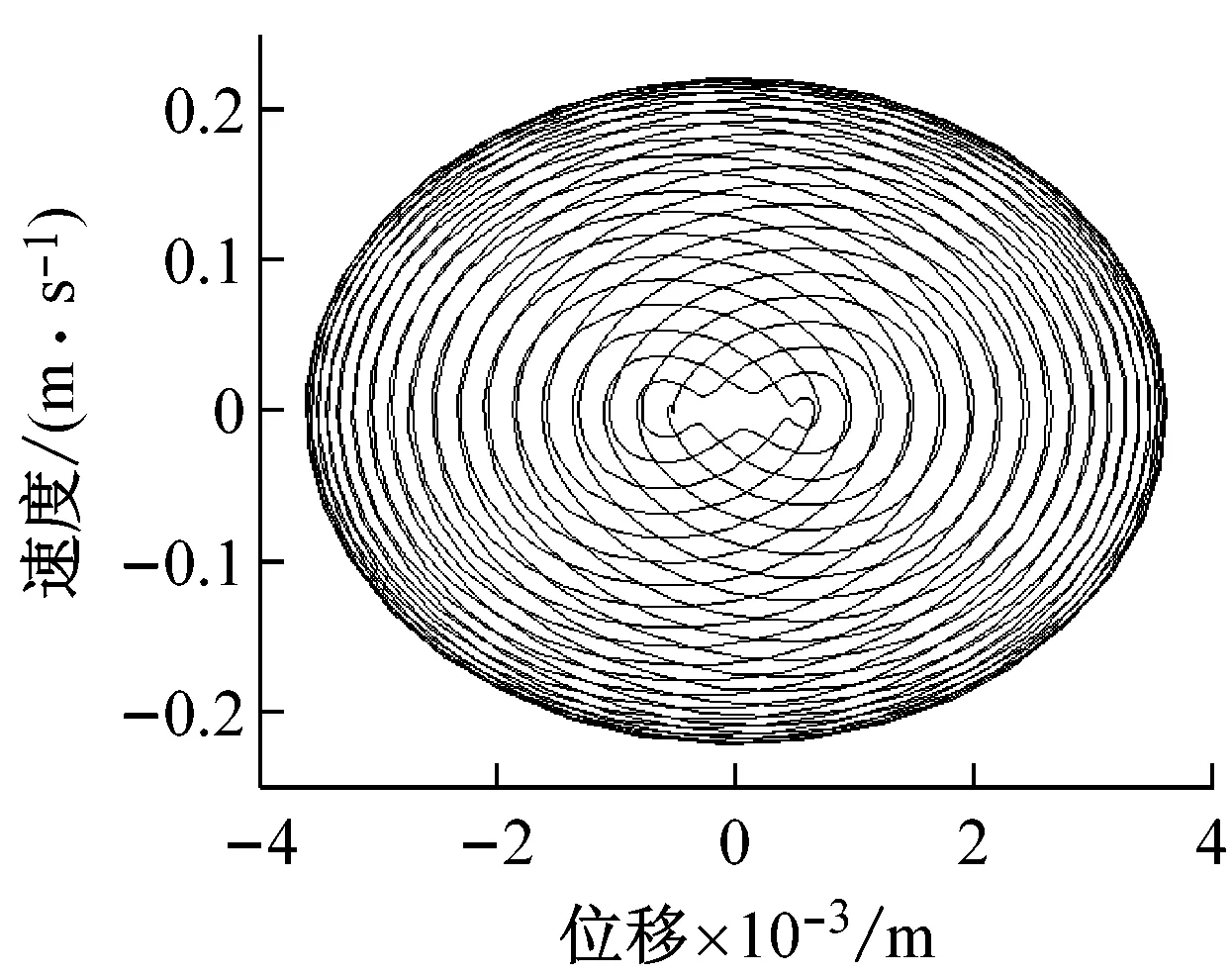
为进一步弱化系统的非线性特性,采用高频小激振力(82 kN)继续改善。在43 Hz和36 Hz较高频双激振参数模拟下,系统的非线性行为得到明显的弱化,图8(a)的相图形成类似双干摩擦模型流形,图8(b)的庞加莱截面成规律的4周期运动,图8(c)的频谱图体现出1/4拍频(43-36=7 Hz)及其高次的亚谐波共振响应,说明压实后期即使激振力减小,激振频率增大,垂直振动模式下,也不可避免振动轮在物料面层上的跳振,应当考虑其他斜向振动和水平振动模式,笔者在参考文献[15]中有研究指出(但该文献仅以单钢轮模型简化)。
(a) 相图
(b) 庞加莱
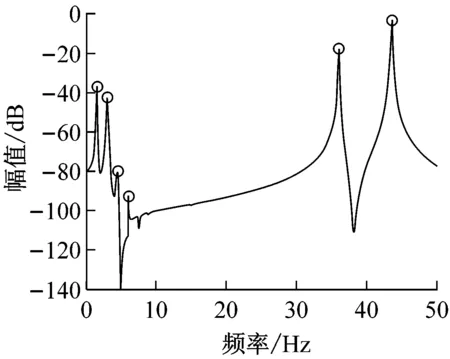
(c) 频域图
3 施工现场压实试验数据分析
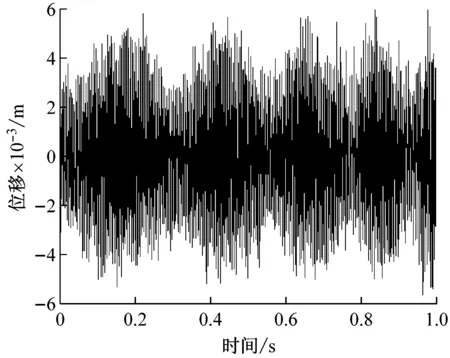
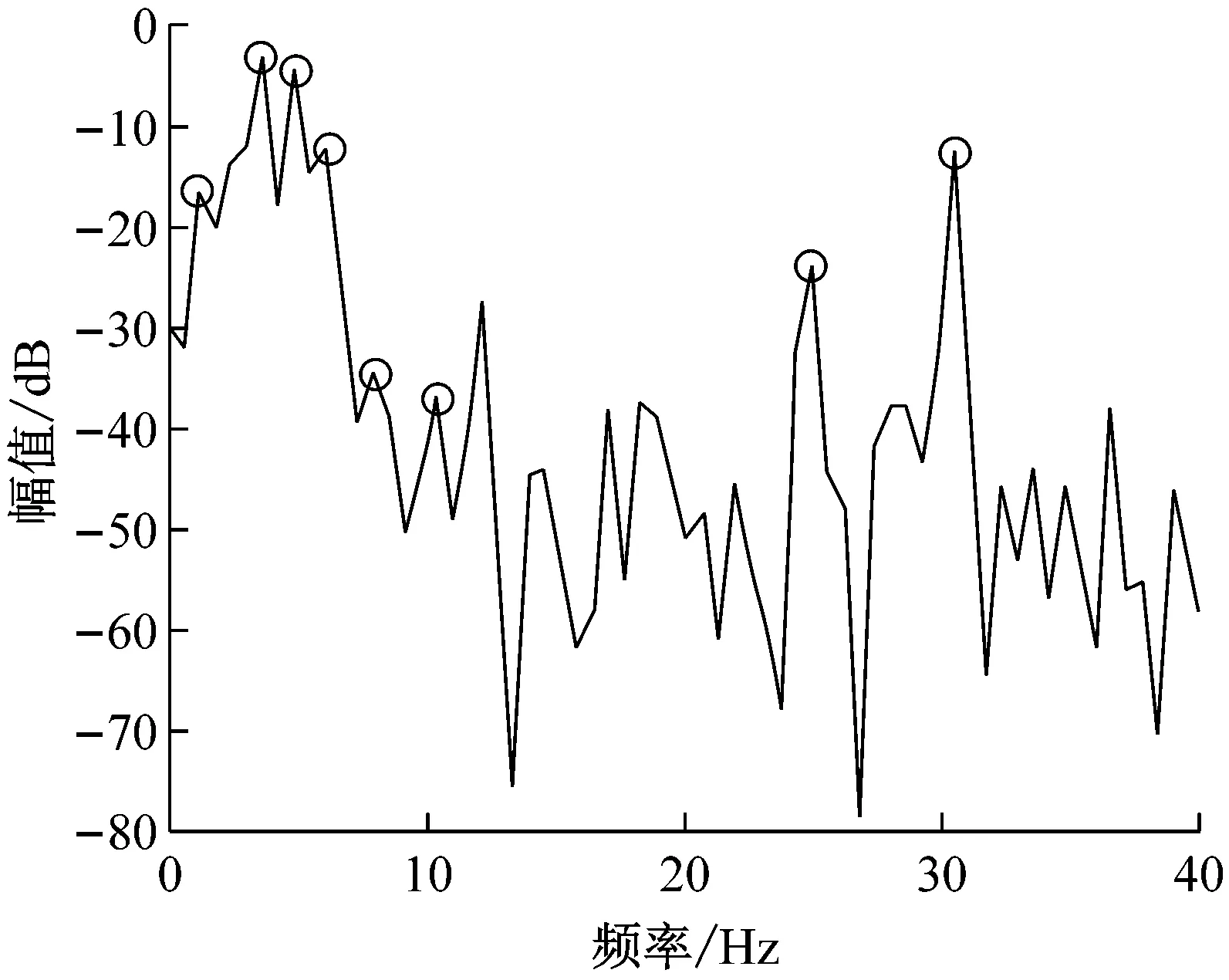
为验证提出模型和理论分析的合理性,采用YZC12双钢轮振动压路机在三明-泰宁路段的沥青施工压实试验数据分析,用3段路基状况大致相同的代表性路段,每个试验路段50 m,压实铺层材料为沥青稳定碎石基层ATB-25,在与理论仿真尽可能的参数相同情况下,以压实2遍代表压实初期、压实4遍代表压实中期和压实6遍代表压实后期。图9(a)是A路段用大激振力(168 kN)压2遍时,放置在驾驶室上的加速度传感器通过YE6262A数据采集系统采集获得的现场试验数据,经YE7600数据分析系统自带的双重积分软件积分获得时域信号,由时域图可以发现在周围环境干扰的情况下仍存在明显的约5 Hz的拍振频率,频域特性图9(b)也可看出驾驶室具有丰富的双激振频率约25 Hz和30 Hz,以及拍频特性成分,在排除环境干扰情况下与模拟仿真效果图4结果基本吻合。
图10(a)是A路段连续压4遍时,驾驶室垂直方向振动信号的时域特性,很明显,当沥青物料进入压实中期时,拍振波形开始发生较为明显的非线性行为,在原来较为明显的5 Hz的拍频基础上,前面两个拍频周期明显大于后面的三个拍频周期,图10(b)的频域特性也可以明显观测到拍频的1/3、2/3、4/3和5/3等亚谐波频率成分,实验数据分析与压实中期参数模拟效果图5结果也基本吻合。
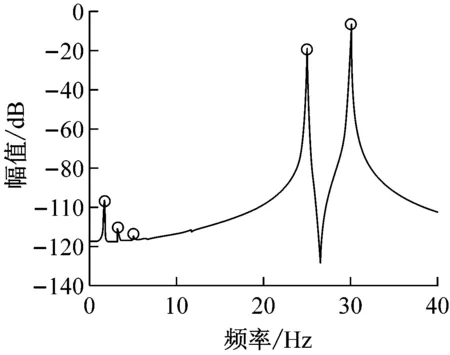
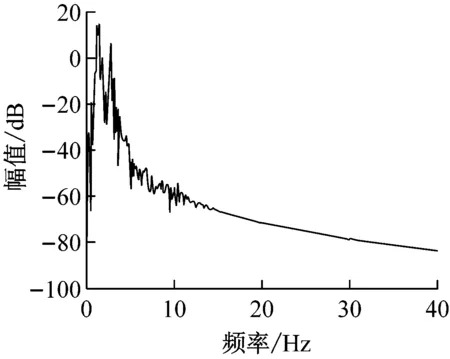
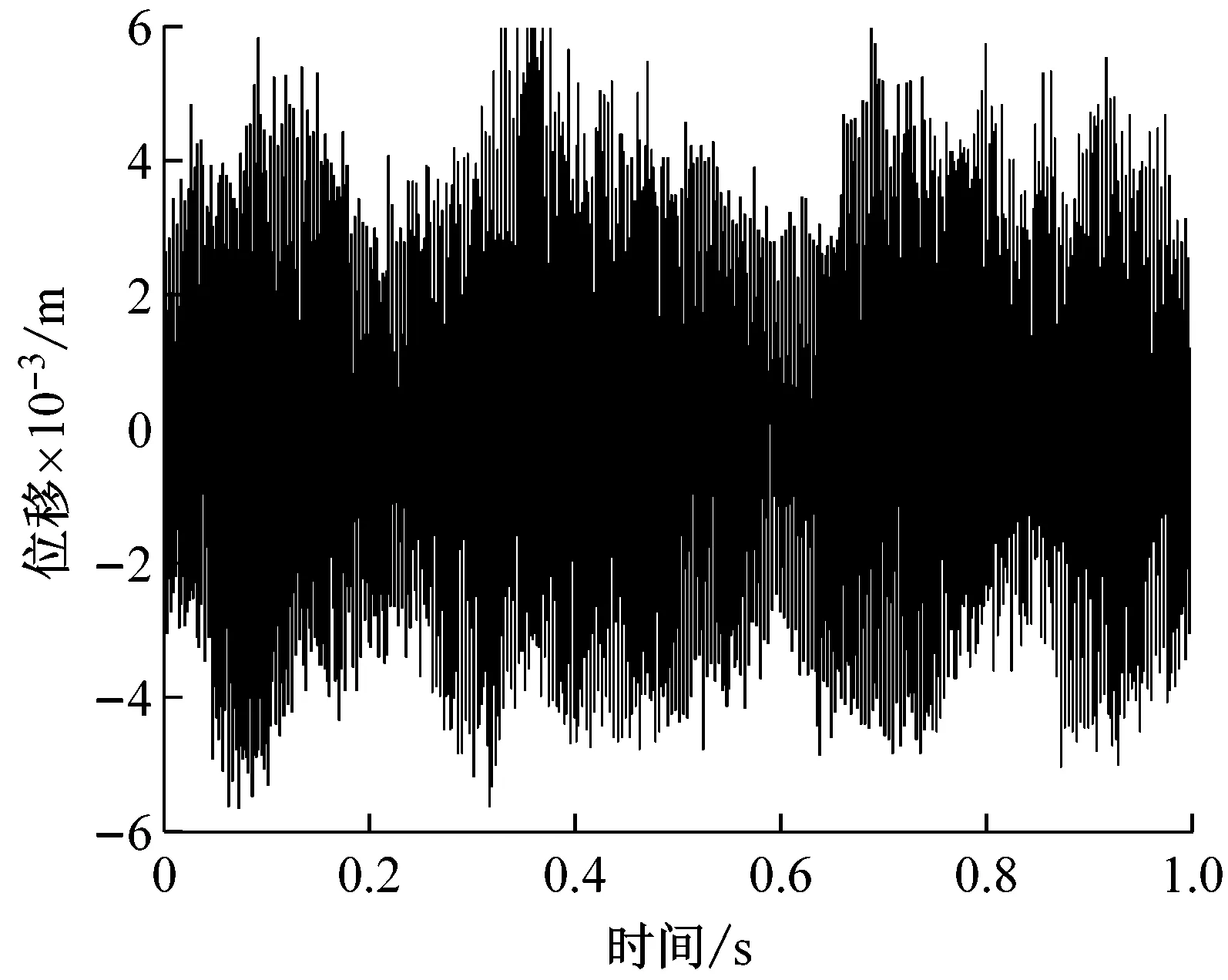
而图11(a)仍是A路段继续压至6遍时,驾驶室底板上采集处理获得的振动时域信号,分析表明,压实后期驾驶室拍振频率成分已经被彻底掩盖,成为无规律周期再现的混沌运动信号,为进一步排除环境干扰,图11(b)的频谱分析图成明显的混沌连续谱,说明在大的振动力和低频激振情况下,前后振动轮在已接近密实的沥青铺层上激烈跳振,导致驾驶室强的非线性混沌振动的发生,该工况下驾驶室乘坐人员有明显的不适感,数据分析结果与参数模拟图6基本吻合。
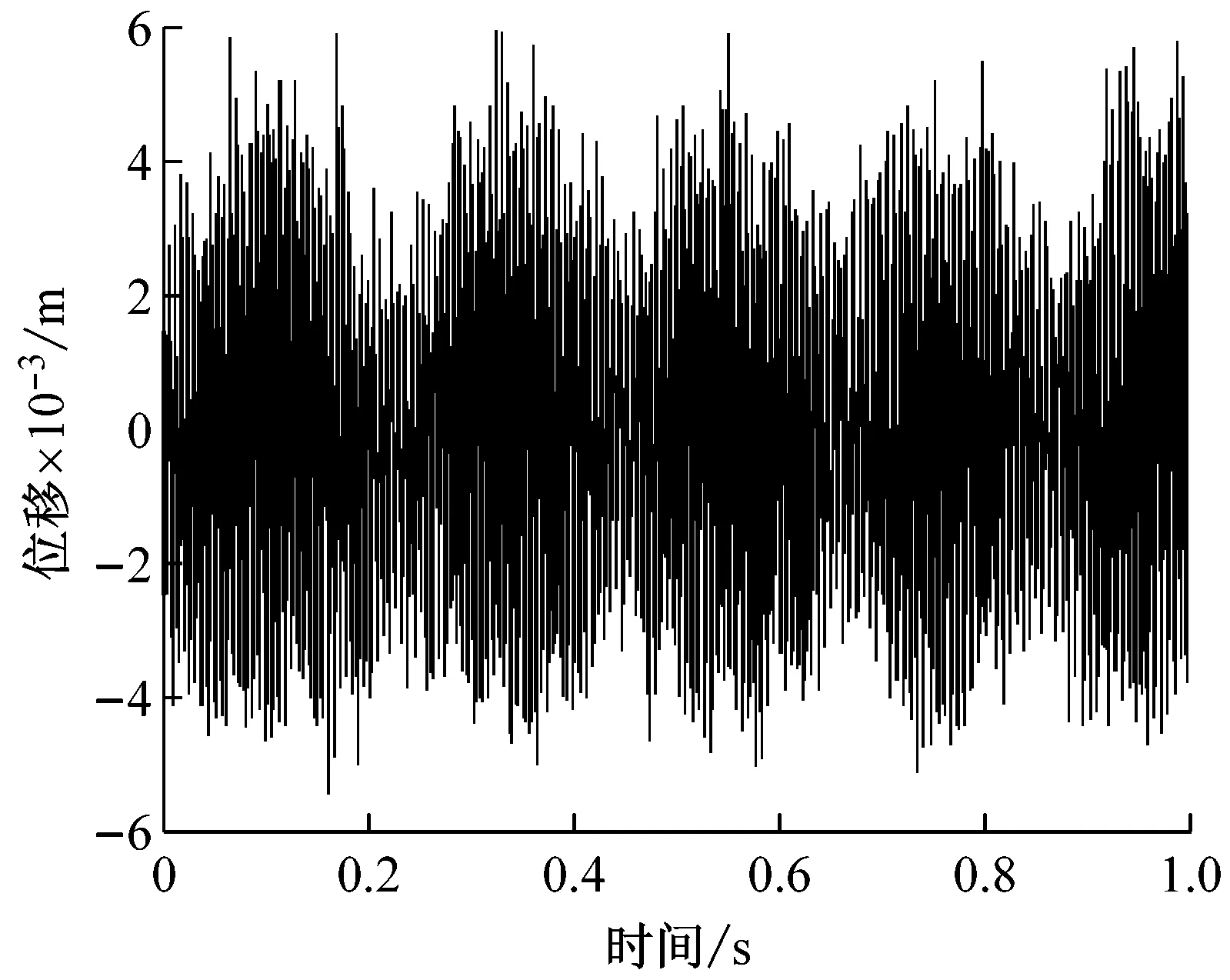
(a) 时域图
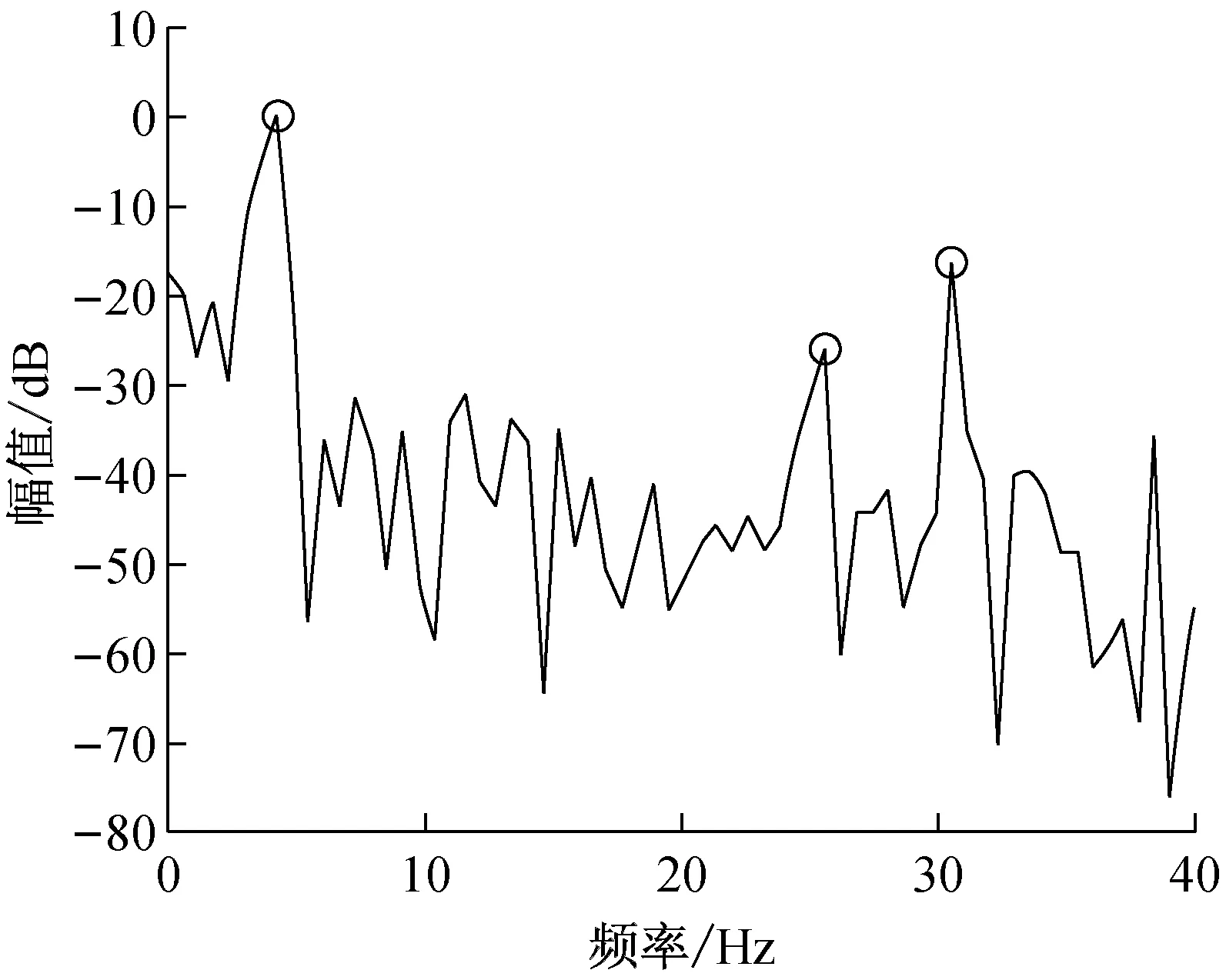
(b) 频域图
Fig.9 Data analysis for section A when compacting 2 passes (i.e. initial compaction stage)
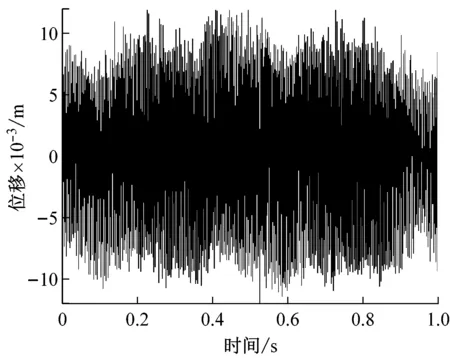
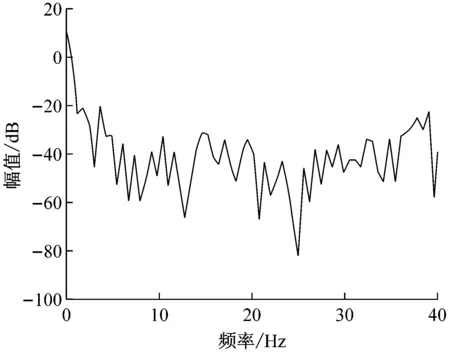
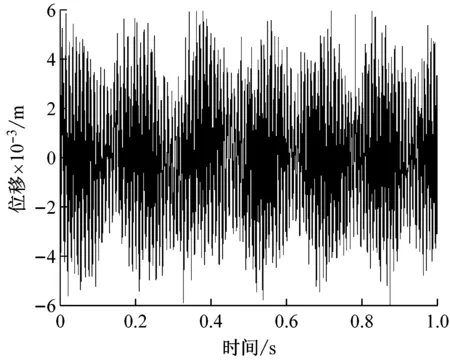
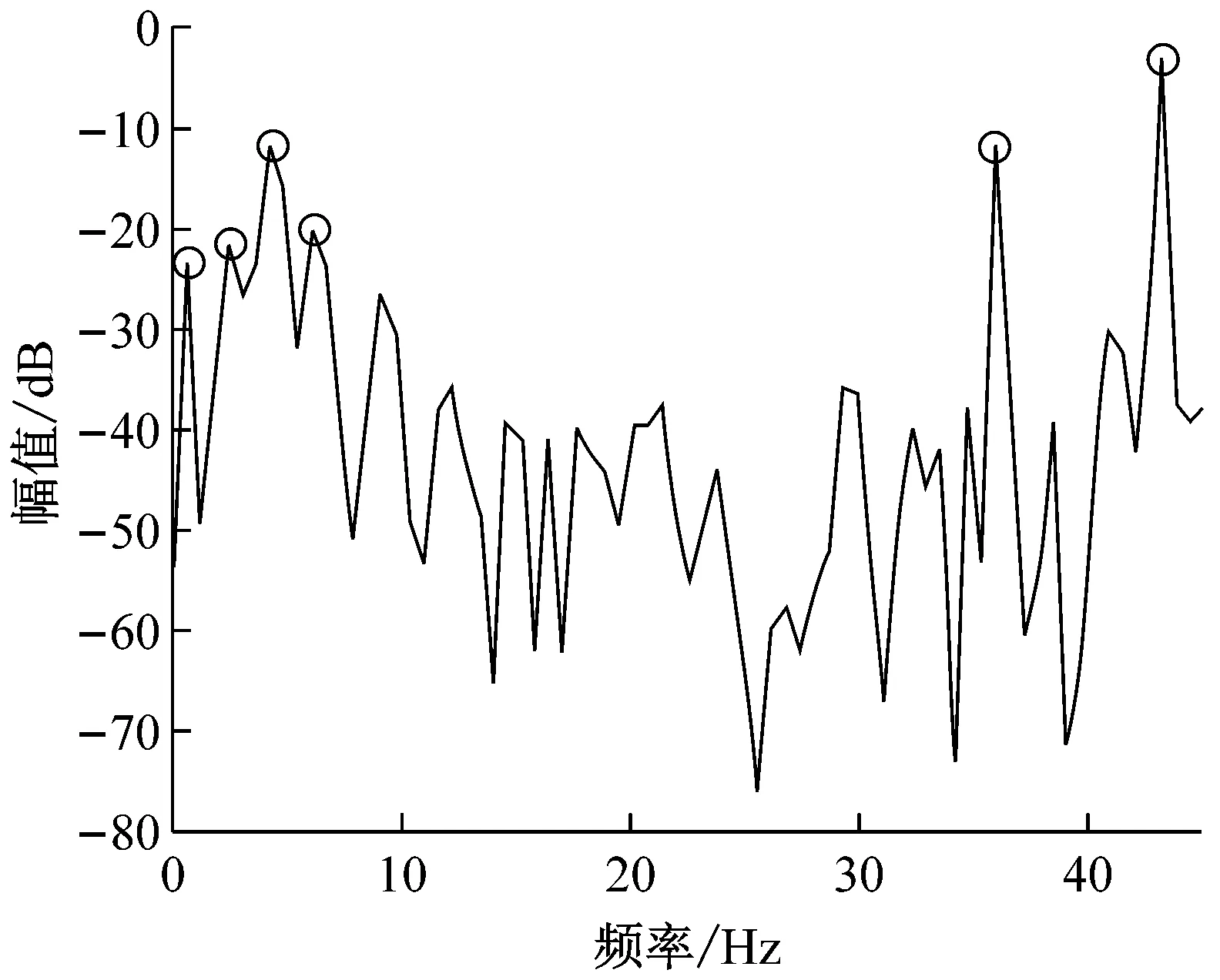
为减小压实后期系统的强非线性特性对压路机结构件使用寿命和驾驶员身心健康的影响,在其他试验条件不变的情况下,采用小激振力(82 kN)来改善后期压实环境工况,图12(a)是B路段压实6遍时,驾驶室上的振动时域信号,由于A和B路段的路基及压实铺层材料级配基本一样,所以可以近似认为A和B路段具有相同的试验条件,具有与图11数据结果的可比性。由图12(a)可以发现,图11的混沌振动响应在激振力减少的改善下,回归到有类似拍振周期信号特征,但非线性特性还是很强烈,第2和3个拍振周期较为模糊,即周期之间的极差一直在变化,图12(b)的频率特性可知,系统除存在丰富的拍频的超谐波共振频率之外,还存在丰富的1/2拍频及其高次的亚谐波成分,双激振频率25 Hz与30 Hz由原来的连续谱已可以明显识别,但拍振频率成分5 Hz能量还是很弱很模糊,与图7的数值仿真效果有较好的吻合。
(a) 时域图
(b) 频域图
(a) 时域图
(b) 频域图
(a) 时域图
(b) 频域图
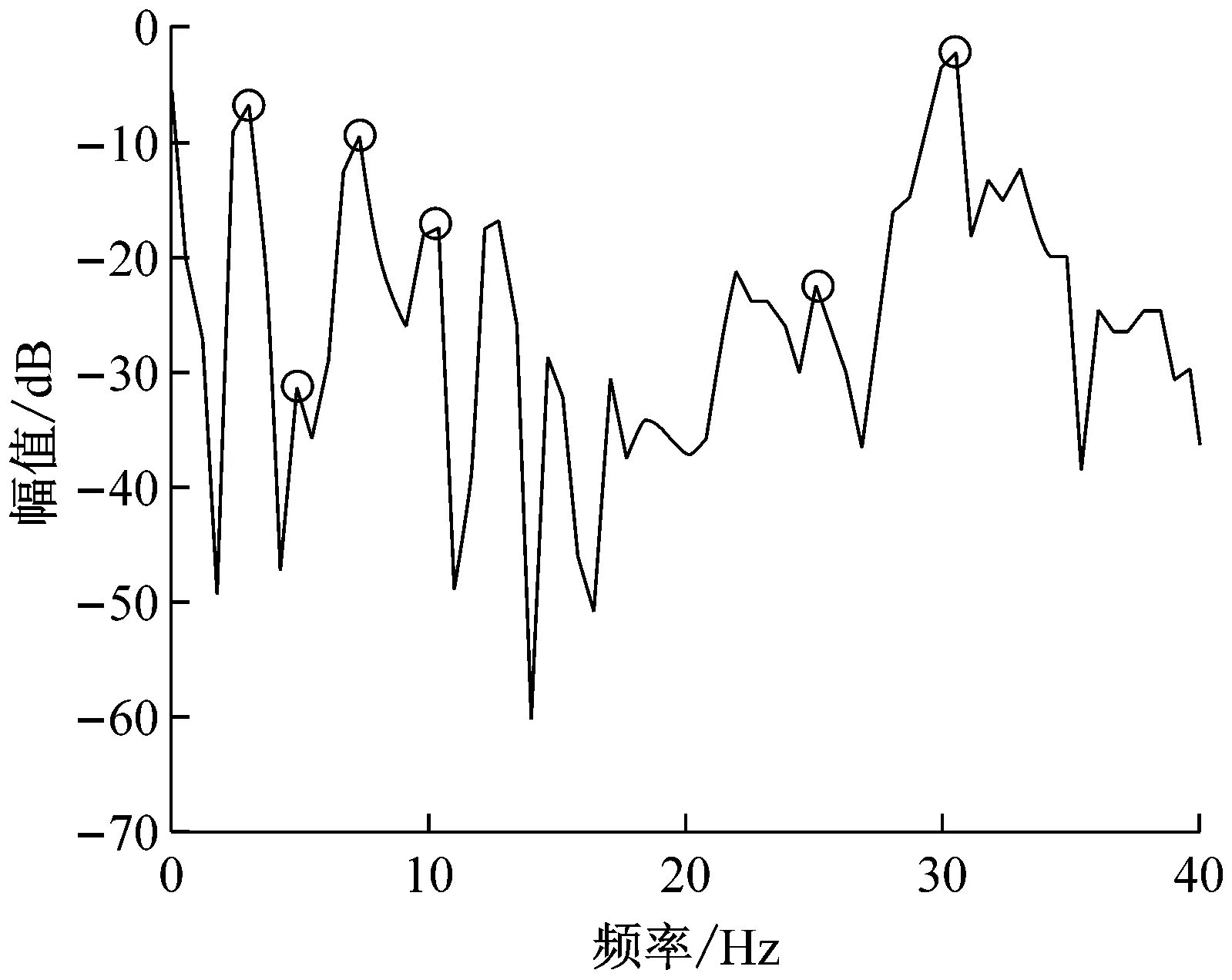
图13是在图12的基础上,采用高频小激振力(82 kN)对具有相同试验条件C路段进行进一步改善压实6遍时的试验结果,图13(b)的频谱图可以发现明显的43 Hz和36 Hz高频成分,和拍频7 Hz及其1/4、2/4和3/4频率成分,非线性特性明显减弱,图13(a)的时域图重新回归到类似压实初期的规律拍振周期响应,说明压实后期,减小激振力和提高双激振频率可以有效地减少振动轮在物料面层起跳的可能,达到良好弱化压实系统的拍振非线性行为效果。
(a) 时域图
(b) 频域图
4 结 论
(1) 根据实际压实工况,建立了双激振压实系统的整体动力学模型,并指出仅前轮跳振、仅后轮跳振、前后轮同时跳振和系统连耦的4工况相互转换,系统体现出比单钢轮动力学模型更为复杂的非线性行为,现场的试验数据证实了提出模型的合理性。
(2) 提出采用三种代表性滞回模型描绘土壤物料压实初期、压实中期和压实后期的弹塑性变形规律,为该领域的机械化施工连续压实密实度在线监测识别提供良好的研究方向。
(3) 双激振钢轮压路机施工过程中,拍振截面非线性甚为敏感,影响驾驶员的身心健康应值得关注,减小激振力和增大前后轮的激振频率可首先弱化驾驶室拍振的非线性,达到有效抑制混沌振动产生的目的,改善了操作舒适性。由于激振力大小和激振频率高低的调整范围受作业效率和作业质量影响,今后还可以从隔振装置设计方面优化研究。
(4) 同时,后续研究可考虑随振土对拍振运动的影响,以更符合实际。
[1] 郑书河,林述温.考虑打滑现象的振动压路机振动轮的滞回响应特性研究[J].振动与冲击,2014, 33(18): 72-77.
ZHENG Shuhe, LIN Shuwen. Nonlinear hysteretic response characteristic of a vibratory drum of a road roller considering slipping[J]. Journal of Vibration and Shock, 2014, 33(18): 72-77.
[2] MINAEV O P. Development of vibratory method for soil compaction during construction[J]. Soil Mechanics and Foundation Engineering, 2011, 48(5): 190-195.
[3] LIU D H, SUN J, ZHONG D H. Compaction quality control of earth-rock dam construction using real-time field operation data[J]. Journal of Construction Engineering and Management, 2012, 138(9): 1085-1094.
[4] YOO T S, SELING E T. Dynamics of vibratory-roller compaction[J]. Journal of the Geotechnical Engineering Division, 1979, 105(10): 1211-1231.
[5] GRABE J. Continuous invers calculation of soil stiffness from the dynamic behaviour of a driving vibratory roller[J]. Archive of Applied Mechanics, 1993, 63: 472-478.
[6] ANDEREGG R, KAUFMANN K. Intelligent compaction with vibratory rollers: Feedback control systems in automatic compaction and compaction control[J]. Journal of the Transportation Research Board, 2004: 124-134.
[7] BEAINY F, COMMURI S, ZAMAN M, et al. Viscoelastic-plastic model of asphalt-roller interaction[J]. International Journal of Geomechanics, 2013, 13(5):581-594.
[8] KENNEALLY B, MUSIMBI O M, WANG J, et al. Finite element analysis of vibratory roller response on layered soil systems[J]. Computers and Geotechnics, 2015, 67:73-82.
[9] ZHU K F, CHUNG J T. Nonlinear lateral vibrations of a deploying Euler-Bernoulli beam with a spinning motion[J]. International Journal of Mechanical Sciences, 2015, 90(1): 200-212.
[10] NAKUTIS Z, KASKONAS P. Bridge vibration logarithmic decrement estimation at the presence of amplitude beat[J]. Measurement, 2011, 44(2): 487-492.
[11] RITENBERG M, BEILIS E, ILOVITSH A, et al. Beating speckles via electrically-induced vibrations of Au nanorods embedded in sol-gel[J]. Scientific Reports, 2014, 4(1): 1-6.
[12] 张会华,吕聪正,李伟.双钢轮振动压路机拍振的仿真分析[J].工程机械,2013, 44(2): 9-15.
ZHANG Huihua, LÜ Congzheng, LI Wei. Simulation analysis of beat vibration for tandem vibratory roller[J]. Construction Machinery, 2013, 44(2): 9-15.
[13] 邓习树,陈乐尧,易全旺,等.双钢轮振动压路机拍振现象分析与研究[J].筑路机械与施工机械化,2008, 25(9): 38-40.
DENG Xishu, CHEN Leyao, YI Quanwang, et al. Analysis and research of clap-vibration phenomenon of tandem vibratory roller[J]. Construction Machinery & Construction Technology, 2008, 25(9): 38-40.
[14] 吕聪正,冯忠绪,李耀,等.双钢轮振动压路机拍振对驾驶室振动影响的研究[J].山东交通学院学报,2013, 21(4): 72-75.
LÜ Congzheng, FENG Zhongxu, LI Yao, et al. On effect of double-drum vibratory roller beat vibration on cab vibration[J]. Journal of Shandong Jiaotong University, 2013, 21(4): 72-75.
[15] SHEN P H, LIN S W. Mathematic modeling and characteristic analysis for dynamic system with asymmetrical hysteresis in vibratory compaction[J]. Meccanica, 2008, 43(5): 505-515.
[16] DENIES N, CANOU J, ROUX J N. Vibrocompaction properties of dry sand[J]. Canadian Geotechnical Journal, 2014, 51(4): 409-419.
[17] SHEN P H. Hysteresis modeling and analysis for dynamic compaction[J]. Advanced Material Research, 2014, 1037: 53-56.
[18] HORAN R D, CHANG G K, XU Q, et al. Improving quality control of hot-mix asphalt paving with intelligent compaction technology[J]. Transportation Research Record, 2012, 2268: 82-91.
[19] 高峰,王娜.振动压路机参数对压实质量的影响[J].建设机械技术与管理,2015, 28(4): 65-67.
GAO Feng, WANG Na. Parameters of the vibratory roller effect on the compaction quality[J]. Construction Machinery Technology & Management, 2015, 28(4): 65-67.
[20] 李雨,赵丽萍,沈建军,等.振动压路机压实过程中的频率稳定性分析[J].中国机械工程,2014, 36(18): 2516-2519.
LI Yu, ZHAO Liping, SHEN Jianjun, et al. Analysis of frequency stability of vibratory roller during compaction stage[J]. China Mechanical Engineering, 2014, 36(18): 2516-2519.
[21] 赵利军,冯忠绪,赵丽萍,等.振动压路机振动轮振幅的探讨[J].西安建筑科技大学学报(自然科学版),2014, 58(2): 297-302.
ZHAO Lijun, FENG Zhongxu, ZHAO Liping, et al. Discussion on the amplitude of vibrating drum of vibratory roller[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2014, 58(2): 297-302.
Analysis and tests for dynamic characteristics of a compacted System under double-excitation
SHEN Peihui1, LIN Shuwen2
(1. Fujian Chuanzheng Communications College, Fuzhou 350007, China;2. College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350002, China)
A double-steel-wheel vibratory roller possesses special vibration characteristics under double-excitation. Considering the asymmetric hysteretic characteristic of soil material in different compacting stages and the possibility of jump-vibration decoupling between the two vibratory wheels in actual working conditions, a 7-DOF overall model was put forward. Using the first order approximation, the equivalent stiffness and damping in different compacting stages were obtained with the harmonic linearization and KBM (Krylov-Bogolyubov-Mitropolsky) combined method. In addition, beat-vibration characteristics of the roller cab due to the difference between vibration frequencies of the front wheel and the rear one were systematically studied. Under model’s parameters in different working conditions, it was shown that Poincare motion sections reflect nonlinear motion characteristics of a single period bifurcation, a double-period one, a three-period one and a multi-period one; the dynamic system produces higher order super-harmonic and sub-harmonic resonances during later compacting stages; with a larger exciting force and a lower frequency condition, the cab enters a chaos vibration; through adjusting excitation forces and the excited frequencies of the double-wheel reasonably, the chaos vibration can be suppressed effectively, the service life of the roller components can be extended and the operating comfort can be improved. The worksite compacting operation tests verified the rationality of the proposed model and theoretical analysis.
compacted system; dynamic model; beat vibration; decoupling; chaos
国家自然科学基金(51175086);福建省高校杰出青年科研人才培育计划(JA11299);福建省交通运输厅科技发展计划(201120);福建省自然科学基金(2015J01186)
2016-03-04 修改稿收到日期:2016-04-19
沈培辉 男,博士,副教授,1977年12月生
TU663
A
10.13465/j.cnki.jvs.2017.11.036
