基于总体平均经验模态分解算法的自适应改进

徐 健， 周志祥， 唐 亮， 冉 杰， 何 杰

(1.重庆交通大学 土木工程学院，重庆 404100; 2.南充市住房和城乡建设局，637000;3.西南交通大学 土木工程学院，成都 610031)

基于总体平均经验模态分解算法的自适应改进

徐 健1， 周志祥1， 唐 亮1， 冉 杰2， 何 杰3

(1.重庆交通大学 土木工程学院，重庆 404100; 2.南充市住房和城乡建设局，637000;3.西南交通大学 土木工程学院，成都 610031)

目前较为广泛使用的总体平均经验模态分解算法(EEMD)不能实现桥梁结构响应信号的自适应分解和重构，基于此，针对EEMD算法的不足，提出了能够实现桥梁结构响应信号自适应分解与重构的改进算法：首先引入自适应极值点匹配延拓算法以抑制端点效应；再对分解信号进行聚类分析以避免模态混叠现象；最后利用各本征模态函数(IMF)对应的信息熵、能量密度和平均周期构建筛选有效IMF分量的指标(有效程度系数)，以实现有效IMF分量的自动筛选，再利用筛选出的有效分量对桥梁结构响应信号进行重构。模拟信号和简支梁桥仿真算例表明，所提改进算法能够更有效、更准确的实现桥梁结构响应信号的自适应分解与重构。

桥梁结构；模态分解算法；端点效应；聚类分析；信号重构

环境激励下桥梁结构的动力信号内部一般会含有大量噪声，且噪声的来源复杂多样，虽然能在数据采集阶段，通过采取平均、滤波和屏蔽等[1]措施来降低振动信号内部的噪声，但要想全部消除噪声是难以实现的。鉴于此，为了在对桥梁系统参数进行辨识、结构进行损伤诊断及健康监测时能得到更为准确的桥梁模态参数，有必要对环境激励下的桥梁结构响应信号进行预处理，通常做法是对信号进行分解和重构。本文通过引入自适应极值点匹配延拓算法、统计学中的聚类分析算法以及信息论[2]中的信息熵、能量密度和平均周期对总体平均经验模态分解算法[3]的改进，以实现对桥梁结构响应信号的自适应分解与重构。

1 总体平均经验模态分解算法

总体平均经验模态分解算法是对EMD算法的重大改进，其具体做法是在原始信号中多次添加等幅值的随机白噪声以改变原始信号中极值点的具体分布，使极值点的分布均匀化，进而在一定程度上避免由间歇性[4]高频分量带来的影响。为了抵消IMF分量中的白噪声，最后需要对所得结果进行几何平均，进而保留具有物理意义的IMF分量。具体实现步骤如下：

(1) 原始信号x(t)中加入N个不同的Gaussian白噪声wi(t)(i=1,2,…,N)，即

(1)

式中：xi(t)为第i次加入白噪声后的信号；wi(t)为第i次加入白噪声。

(2) 对加入了白噪声的信号xi(t)分别进行EMD分解，得到相应的IMFij和一个余项rij，其中IMFij(j=1,2,…,n)表示第i次加入白噪声后分解所得的第j个IMF，即：

(2)

式中：i表示每次EMD分解得到的IMF和r的总个数。

(3) 利用不相关随机序列的统计均值为0的原理，将上述对应的IMF进行总体平均运算，得到EEMD分解后最终的IMF，即

(3)

式中：IMFj为对原始信号进行EEMD分解后所得的第j个IMF。

EEMD算法的基本流程图，如图1所示。

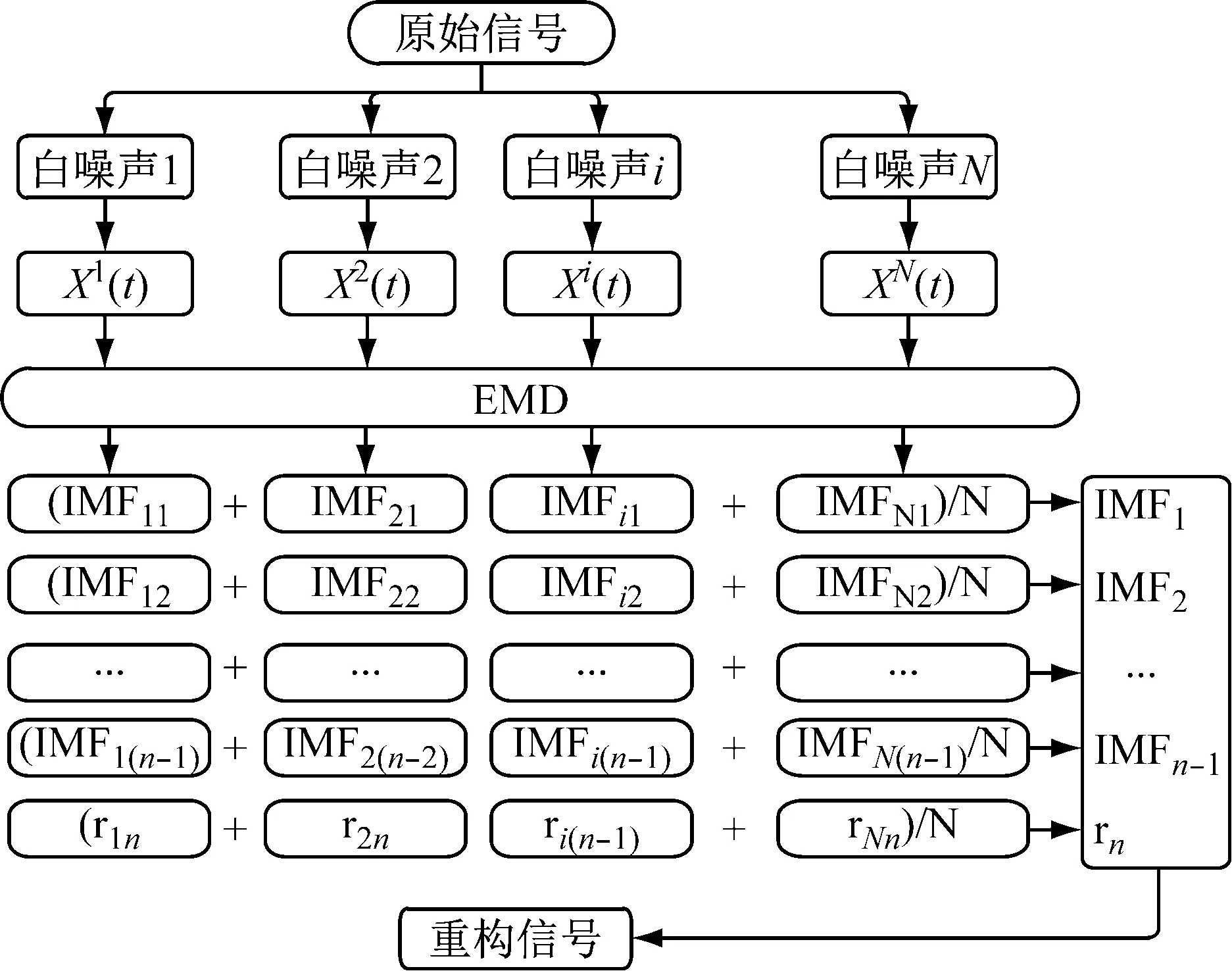
图1 EEMD基本流程图

2 总体平均经验模态分解算法的改进

通过EEMD算法的基本原理及分解效果可知：其存在以下几个方面的缺陷：端点效应的处理效果不佳；所得本征模态函数之间依然存在模态混叠现象；难以准确筛选有效的IMF分量用于信号重构，针对上述三方面的缺陷，本文提出了相应的改进算法。

2.1 正负白噪声的添加

EEMD分解过程中，需要在原信号分解中添加白噪声信号，再进行分解，这样不同时间尺度的信号成分会被自动分解到由白噪声信号所确定的通频带中，能在一定程度上克服模态混叠现象[5]。但是由于在原信号中添加了白噪声信号，白噪声信号会造成原信号的“污染”，使得分解结果信噪比降低。由于不能完全消除白噪声带来的影响，导致该算法的重构误差较大，分解的完备性较差。基于此，本文对原始信号添加正、负白噪声以解决上述问题，具体的步骤如下：

(1) 向原信号s(t)中添加随机的白噪声，其中包括K组正的白噪声ni(t)和K组负的白噪声-ni(t)，计算式为

(4)

式中：q=1,2(等于1时代表加入的是负的白噪声，等于2时表示加入的是正的白噪声)；i=1,2,…,K，K代表加入白噪声的总次数；a0代表添加白噪声的幅值标准差；ni(t)代表第i次添加的白噪声；s(t)代表原始信号；x(t)代表添加了白噪声之后的信号。

(2) 将加入了正、负白噪声对的混合信号x(t)作为EEMD模态分解算法的输入进行分解。

在实际应用中，添加的白噪声幅值不能太大，也不能太小；如果白噪声幅值太大，则噪声会掩盖住有效信号，且残留噪声也难以剔除；如果白噪声幅值太小，则不足以改变原信号中的极值点分布，达不到消除模态混叠现象的效果。相关学者[5]研究表明：添加的白噪声幅值常取原始信号标准差的0.1倍～0.2倍。

2.2 自适应极值点匹配延拓

针对EEMD算法中的端点效应问题，目前已有许多学者提出了改进方法，改进算法大致分为以下两大类：

(1) 极值点延拓法[6]：将原始信号数据向外延拓一定数量的极值点，该算法的优点在于操作简单，容易实现；缺陷在于仅仅只考虑了信号在端点处的局部信息，未能从信号的整体进行考虑，存在局限性；

(2) 预测延拓法[7]：即采用神经网络[8]、ARMA模型[9]、支持向量机法[10]等对原始信号进行数据预测延拓。这类算法对端点效应的处理效果主要取决于参数设置，不具有自适应性，且计算量大，运算时间长。

本文结合上述两类方法的优缺点，提出了一种新的延拓方法，即自适应极值点匹配延拓算法，该算法的主要特点在于：能从原始信号内部找出与信号两端极值点最匹配的极值点对信号进行延拓，这样既最大限度的考虑了原信号的内部规律，又能快速的实现，具有一定的自适应性。该算法的基本原理如下：

设信号为x(t)，mi,ni(i=1,2,3…)分别为极大值点和极小值点，对应的时间分别为tmi和tni。以信号x(t)左端点延拓为例，xtx1为信号左端起点，以xtx1-m1-n1三点构成极值点特征波，然后从信x(t)中寻找和特征波最匹配的极值点波形，xtxi-mi-ni作为匹配极值点波，将匹配极值点延拓到原信号左端点前(右端延拓到右端点)。具体步骤如下：

(1) 求出除左端点xtx1外的所有xtxi，对此先由相似关系求出其对应的时间值txi；

(5)

其中假定tm1小于tn1，若求出的txi不在采样点上，可以对其线性插值求出xtxi的具体值。

(2) 计算所得的极值点与特征极值点的误差e；

(6)

式(6)中之所以除以第一个极大值、第一个极小值以及信号端点值是为了对误差值进行标准化处理；

(3) 找出最小的匹配误差e(i)min，此时的极值点即为匹配极值点，将匹配极值点的数据作为延拓极值移至原信号左端点处；

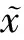
上述延拓算法，不仅考虑了信号的整体趋势和规律，而且只需要延拓极值点，操作简单，相比其它方法具有更强的自适应性。

现阶段，一般通过直接观察法来判定信号端点效应的处理效果，基于此，引入了用于评价端点效应处理程度的评价指标θ，基本原理是：通过比较分解前后的能量来评估端点效应的影响程度，具体计算流程如下：

(1) 首先计算原始信号与各IMF分量的均方根有效值RMS，并用该值来估计各信号序列的能量大小，RMS的具体计算式子为

(7)

式子中：S(i)：信号序列，即原始信号x(t)或各IMF分量；

n：信号采样点数。

按照(7)计算比较各IMF分量的有效值总和与原信号有效值，得到评价指标θ。

(8)

式子中：RMSx代表原始信号的有效值；RMSf代表第f个IMF分量的有效值；k代表IMF分量总个数，包括信号分解结果中的残余量。

由定义可知：当θ=0时，表明不存在端点效应；θ值越大时，则端点效应影响越大。

2.3 模态混叠现象处理

利用EEMD算法分解信号时，所得IMF间可能会存在模态混叠现象，即相近的特征时间尺度会分布在不同的IMF分量中，导致相邻的两个IMF分量波形混叠，相互影响，难以辨认。分析其原因主要是因为：EEMD算法在求取IMFj时只是直接对IMFij(i=1,2,…,N)求平均，却未考虑同一行的N个IMFij(i=1,2,…,N)是否属于同一类。同时，同一列的n-1个IMFij(j=1,2,…,n-1)间也有可能存在模态混叠现象；基于此，本文引入了多元数据分析方法中的聚类分析[11]以解决模态混叠问题，具体实现过程如下：

(1) 在对信号进行模态分解的过程中，每次分解都会得到一系列的IMF分量，为了保证这些分量之间不存在混叠现象，可以利用聚类分析对每次得到的分量进行分析，一旦所得分量之间存在模态混叠，则舍去该组结果，并重新添加白噪声进行EMD分解，直到分解结果中不存在模态混叠现象为止；

(2) 对同一行的N个IMFij进行聚类分析，以筛选出聚类个数最多的一类IMF，然后再对其取平均作为最后的IMFj。

通过将聚类分析算法引入到EEMD算法流程中，不仅能够很好的保证每次分解得到的IMF分量之间不存在模态混叠，且还能保证最后所得的本征模态函数之间不存在模态混叠现象。

2.4 有效IMF分量的筛选

利用EEMD算法对信号进行模态分解时能得到多个本征模态函数(IMFs)，但却不能实现有效IMF分量的自动筛选，实际操作中往往需要根据各IMF分量的Hilbert-Huang谱来人为参与有效IMF分量的筛选，这样不仅会降低工作效率，还会因为个人的差异性导致筛选结果存在主观性。基于此，本文提出了一种综合考虑各IMF分量信息熵[12]，能量密度和平均周期[13]的筛选算法，以实现对各有效IMF分量进行自动筛选，避免主观因素的影响。现对信息熵、IMF分量的能量密度以及平均周期介绍如下：

(1) IMF分量的信息熵

对响应信号进行模态分解，可以得到一系列不同带宽的IMF分量，每个分量包含了信号从高到低的不同频率成分，且这些频率和带宽都会随着信号的变化而变化。通过对信息熵的研究发现，当IMF分量中所包含的信号成分越有序、时频分布的聚集性越好，信息熵的值将会越小；反之，若IMF分量中包含的信号成分越无序、时频分布的聚集性越差，信息熵的值越大。以下就如何计算各IMF的信息熵进行分析：

1) 假定f(t)是信号x(t)模态分解之后所得IMF中的一组分量，f(t)中的最大值为fmax，最小值为fmin；

2) 设置区间[fmin,fmax]中的N等分点Ai，[fmin,A1],(A1,A2],…,(AN-1,fmax]这N个区间作为特征量的N各离散值域B∈{B1,B2,…,BN}，当某个样本的该属性的值落入(Ai,Ai+1]区间时，就认为该样本在该属性上具有相应的离散属性值Bi；

3) 当离散信号的采样点总数为n，f(t)落在第i个区间的样本点个数为mi，则可以根据统计学f(t)落在第i个区间的概率P(Bi)=mi/n。接着根据信息熵的第3定义[15]可得该IMF的信息熵为

(9)

(2) 能量密度与平均周期

根据文献[15]的研究报告可知：对于添加了白噪声序列的信号而言，当利用EMD对其进行模态分解时，所得的各IMF分量的能量密度与其平均周期的乘积是一个常量，基于此，提出了一种筛选IMF分量的算法，具体实现过程如下：

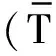
(10)

式中：N为原始信号的长度；fj为第j个IMF分量的振幅值；Oj为第j个IMF分量存在的极值点个数。

2) 利用每个IMF分量的能量系数(ET)来计算每个IMF分量最终的有效系数RP，计算式为

(11)

当第j个IMF分量对应的有效系数RPj≥1时，则说明第j个IMF分量对应的能量系数相比于前面的j-1个IMF分量的能量系数的平均值成倍数增大，此时则可以认为前面j-1个IMF的能量密度与其平均周期的乘积为一个常量，即前面j-1个IMF分量可以被看作是噪声被删除掉，这样留下的便是有效的IMF分量。

(3) 综合评价算法

如果只是根据各IMF分量的信息熵来选择有效IMF，则筛选的结果有可能会有误差，所以本文将信息熵(H)与有效系数(RP)结合起来，提出了综合评价算法[14]。该算法是一种基于模糊数学的综合评标方法，主要是根据模糊数学的隶属度理论把定性评价转化为定量评价。可以利用信息熵和有效系数构造了一个新的指标(有效程度)来量化各IMF分量与原始信号之间的有效程度(Y)，具体计算公式为

(12)

式中：wH为信息熵H的权重；wRP为有效系数RP的权重。

文献[14]中有关于权重大小值的确定，综合考虑信息熵与有效系数之间的主次，假定公式(12)中两权重系数都为0.5。

wf=0.5综合上述分析可知：当Yi越接近1，表明第i个IMF分量与原始信号的相识程度越高，结合文献[14]，本文假定当Y≥0.8γi>0.3时，则认为该IMF分量为有效IMF。最后对所有的有效IMF分量进行求和，便能得到最终的重构信号。改进EEMD算法的流程图,见图2。

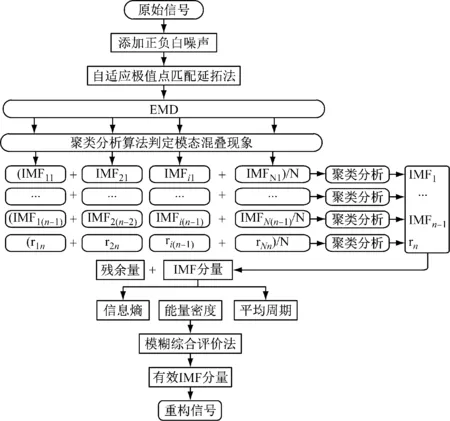
图2 改进EEMD算法流程图

3 仿真信号验证

现利用改进的EEMD算法和EEMD算法对模拟信号进行模态分解，并将所得结果进行对比分析。模拟信号由1 Hz、3 Hz以及7 Hz的正弦信号叠加噪声水平约为10%的随机噪声组成，模拟信号可表示为

s(t)=7sin(14πt)+3sin(6πt)+sin(2πt)+10rand

模拟信号中的时间为10 s，每0.01 s一个测试点，即1 000个测试点。叠加信号以及各信号和噪声的时域图,如图3所示。

图3 信号与噪声

分别运用改进EEMD算法和EEMD算法对上述模拟信号进行模态分解处理，现将两种分解方法所得结果对比分析如下。

3.1 端点效应对比分析

两种分解算法对应的IMF分量结果图如图4和图5所示，对比分析图4中IMF3-IMF5与图5中IMF2-IMF4，可得如下结论：

(1) 根据IMF分量在两端点处的波形形状可知，改进EEMD算法能改善EEMD分解结果存在的端点效应问题；

(2) 采用1.2节中的端点效应评价指标进行定量判定，可得EEMD算法对应的评价指标为0.735 8，而经过自适应极值点匹配延拓法处理过后的评价指标为0.008 4。

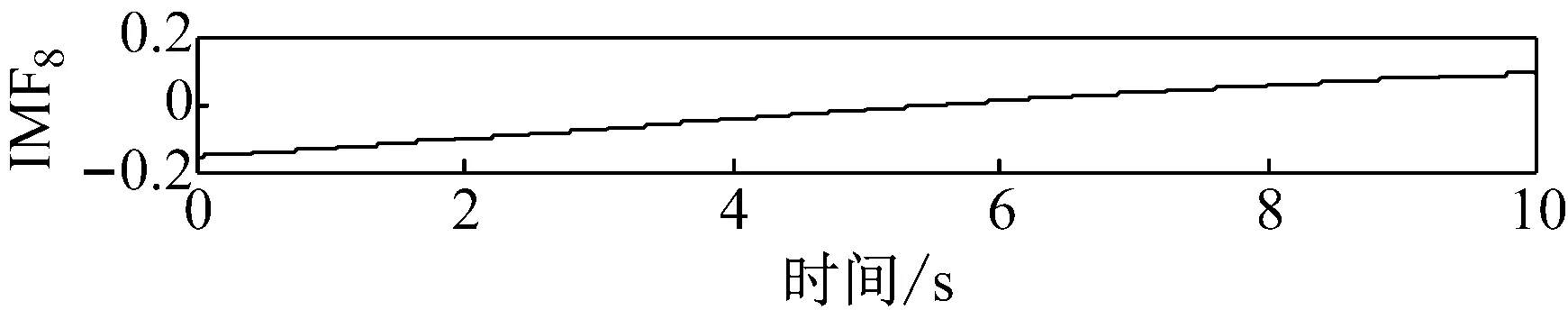
图4 分解结果(改进EEMD)

图5 分解结果(EEMD)

综合上述，本文所提自适应极值点匹配算法能有效改善EEMD算法中存在的端点效应问题。

3.2 模态混叠现象对比分析

为了验证所得IMF分量之间是否存在模态混叠现象，分别对两种分解算法所得的IMF分量进行聚类分析，聚类结果见图6和图7，通过对比分析两图可知：

(1) 由图6可知：各IMF分量都是单独的一类，即各IMF分量之间不存在相似的信息，表明该分解算法所得IMF分量之间不存在模态混叠现象；

(2) 由图7可知：IMF6和IMF7被划为了同一类，表明这两分量间含有一定的类似信息，即存在模态混叠现象。

综上可知：本文所提的聚类分析算法在信号分解过程中，能有效避免模态混叠现象的产生。

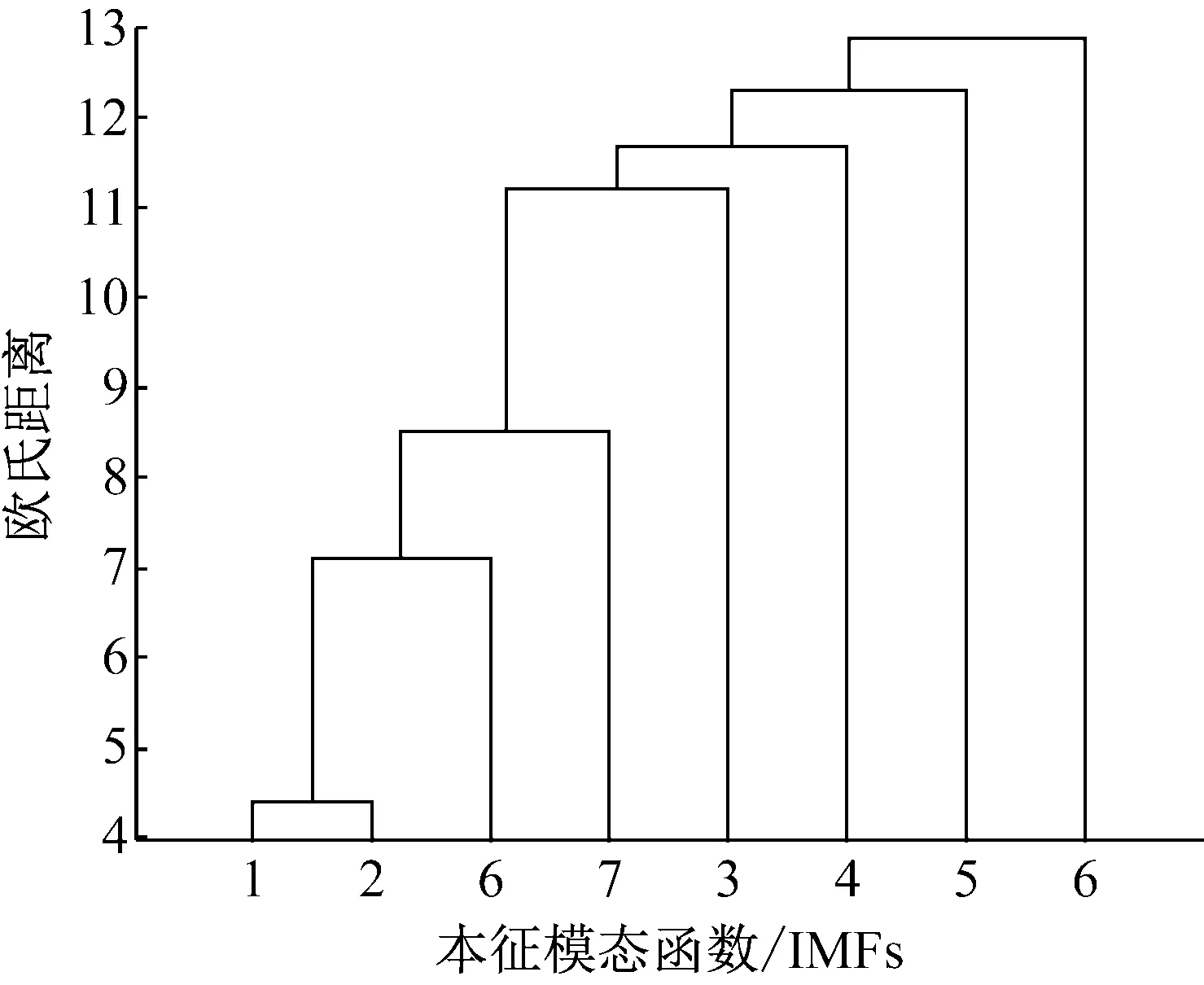
图6 聚类结果(改进EEMD)

3.3 有效IMF分量的筛选

为了解决EEMD算法不能筛选有效IMF分量的这一缺陷，提出了综合评价算法，即利用各IMF分量的信息熵、能量密度以及平均周期构建筛选指标，用于筛选有效IMF分量，具体分析结果见表1和表2。通过对比两表中的数据可得如下结论：

表1 有效程度系数表(改进EEMD)

表2 有效程度系数表(EEMD)

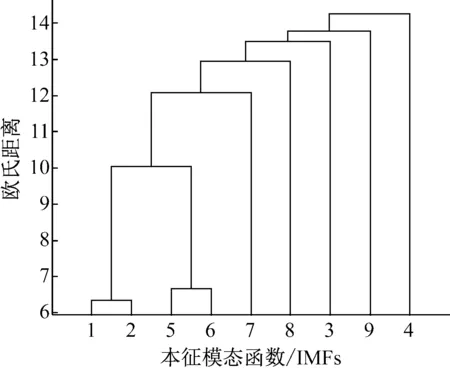
图7 聚类结果(EEMD)

(1) 根据表1可知：IMF3、IMF4和IMF5对应的有效程度系数大于0.8，即为有效的IMF分量，能用于重构信号；

(2) 根据表2可知：IMF2、IMF3和IMF4对应的有效程度系数大于0.8，即为有效的IMF分量，能用于重构信号；

通过将筛选出来的IMF分量与图4和图5所示的分解图进行对比分析，可知：本文所提综合评价算法能筛选出叠加信号中对应的7 Hz、3 Hz以及1 Hz信号，表明该算法能实现有效IMF分量的自动筛选。

为进一步验证改进EEMD算法能更好的处理端点效应，给出了两种分解算法所得结果中有效IMF分量对应的瞬时频率，如图8和图9所示。对比两图可知：两种分解算法均能凸显模拟信号的频率成分；对比瞬时频率在端点处的变化情况可知：本文所提改进EEMD算法能更好的处理端点效应。

4 简支梁桥仿真算例

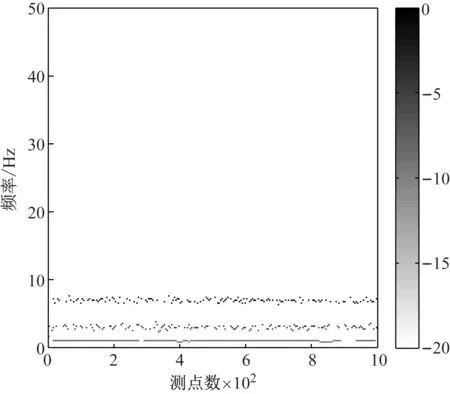
图8 Hilbert-Huang(改进EEMD)

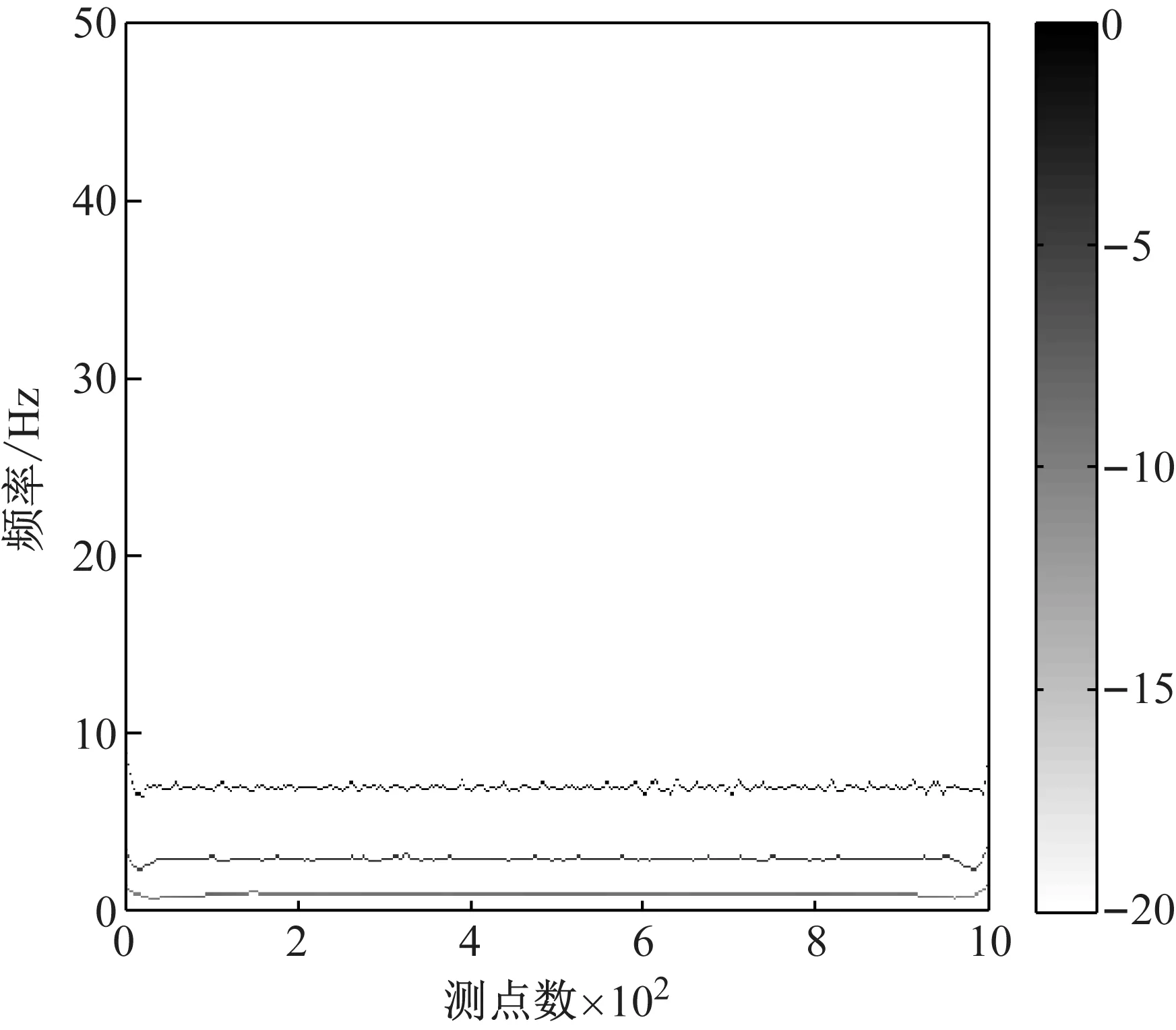
图9 Hilbert-Huang(EEMD)

为进一步验证改进EEMD算法能被运用于处理桥梁结构的动力响应信号，现建立一座混凝土简支梁桥模型，通过施加白噪声激励的方式来模拟环境激励，并采集100组白噪声激励下各节点对应的加速度响应信号；接着分别利用EEMD算法和改进EEMD算法对加速度响应信号进行分解和重构，最后利用随机子空间算法(SSI)[15]对重构的信号进行模态参数识别，并对比分析所得参数结果以验证本文所提算法的可行性及可靠性。

4.1 简支梁桥模型

该简支梁桥模型为单跨，跨度为40 m，截面采用箱型截面，具体截面尺寸见图10(b)。本文采用MIDAS软件进行建模，单元个数为10个，类型为一般梁单元，沿跨径方向共11个节点，在除了端点处的2-10号节点处分别施加竖直方向的白噪声激励，用于模拟实际情况下的环境激励。简支梁桥模型,见图10所示。

4.2 有限元计算

本文主要研究桥梁结构的竖向模态，所以添加的白噪声激励方向为竖向，激励的采样频率为100 Hz，根据采样定理，竖向模态中提取频率小于数值模拟过程中采样频率的一半，即50 Hz。利用MIDAS软件可得该简支梁桥前三阶频率和模态振型，见图11所示。

(a)简支梁桥(b)截面图(cm)

图10 简支梁桥模型

Fig.10 Simply supported girder bridge model

(a) 第1阶振型

(b) 第2阶振型

(c) 第3阶振型

图11 模型前3阶振型

Fig.11 The first three mode of vibration

4.3 环境激励的模拟

为了模拟环境激励，采用在MIDAS模型中施加白噪声激励的方式，所谓的白噪声是指功率谱密度在整个频域内均匀分布的噪声。白噪声的具体添加过程如下：

(1) 利用Matlab软件中的randn命令生成均值为0，方差为1的随机序列100组；

(2) 将这些方向相同但大小不同的白噪声激励施加在简支梁除端点的节点处；

(3) 进行时程分析，并提取相关响应信号。

图12是MATLAB软件利用randn命令产生的一组均值为0，方差为1随机序列，即白噪声激励。

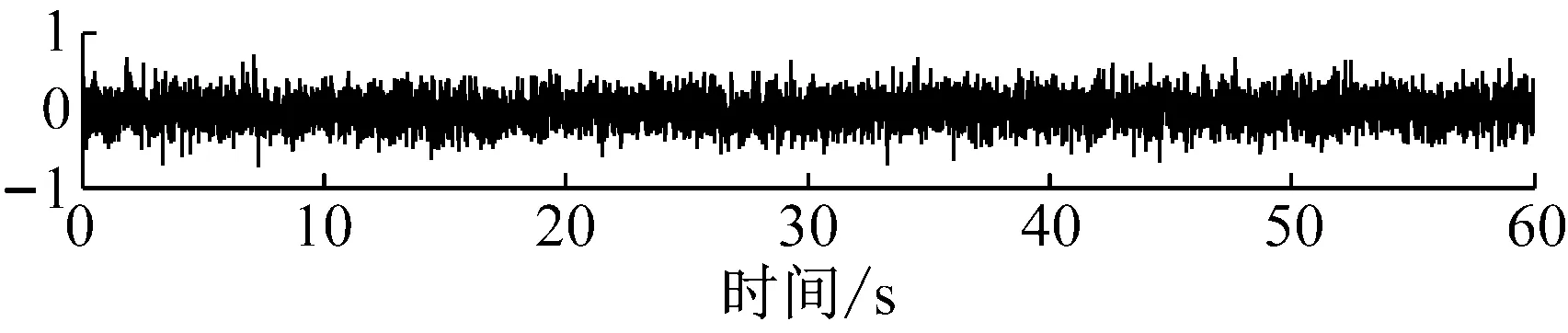
图12 白噪声激励

4.4 数值模拟的结构响应

简支梁桥模型中，节点号2-10处都施加了竖向的离散白噪声激励，且各激励点的白噪声序列各不相同。加载的时间为60 s，时间间隔为0.01 s，相当于100 Hz采用频率进行采样。通过时程分析，可以得到各点处的加速度响应。为更形象地模拟环境激励，对各节点的加速度响应添加20%左右的白噪声，添加了白噪声之后的3、6和9号节点对应的加速度时程曲线见图13所示。

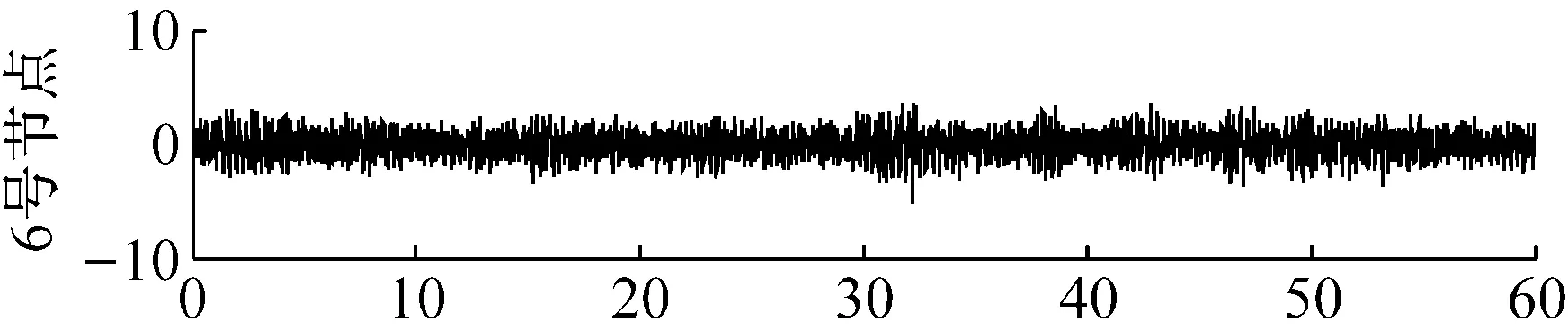
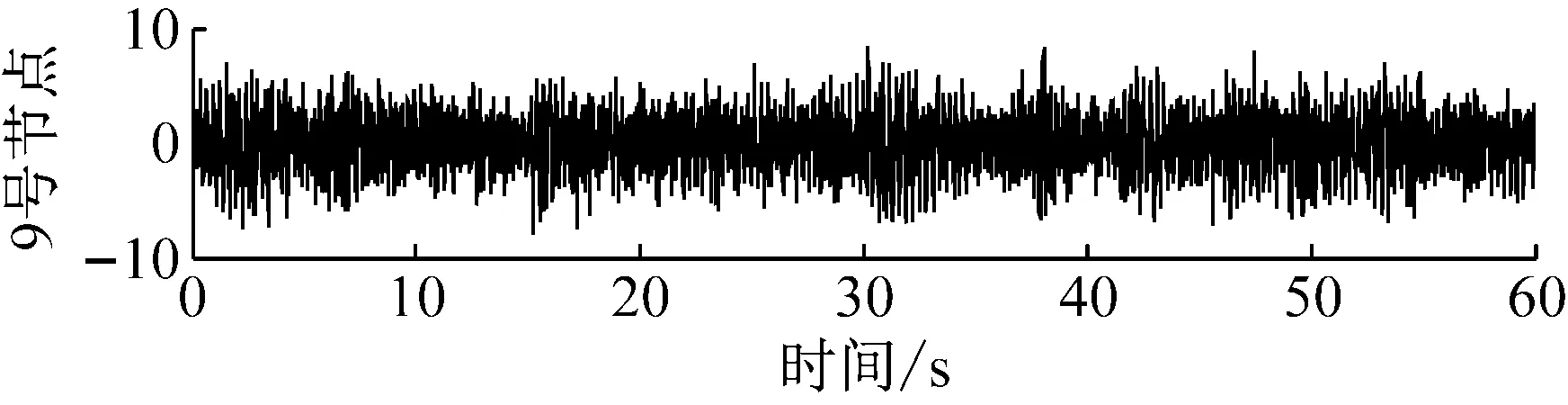
图13 节点加速度响应(m/s2)

4.5 模态参数识别结果对比

分别利用EEMD算法和本文算法对各节点的加速度响应信号进行分解和重构，接着利用随机子空间算法(SSI)识别该简支梁的模态参数，包括频率值、阻尼比以及模态振型。表3给出了各算法对应的频率值结果，图14和图15分别是EEMD预处理和改进EEMD算法预处理结构信号后，利用SSI算法得到的稳定图，对比分析两稳定图可得如下几点结论：

(1) 第一阶和第二阶模态：经EEMD算法预处理的信号，其稳定图中存在明显的虚假模态；而经本文算法预处理的信号，得到的稳定图中却不存在虚假模态；

(2) 第三阶模态：两种算法预处理信号之后得到的稳定图中都存在虚假模态，但本文算法预处理信号之后得到的稳定图中虚假模态更少，且虚假模态的连续性很差；

(3) 对比表 3中的数据可知：本文算法预处理信号之后识别出的频率值更接近真实值。

综合上述，本文算法相比EEMD算法而言，能更为有效地消除环境激励下信号中存在的噪声，能更好实现信号的分解与重构。

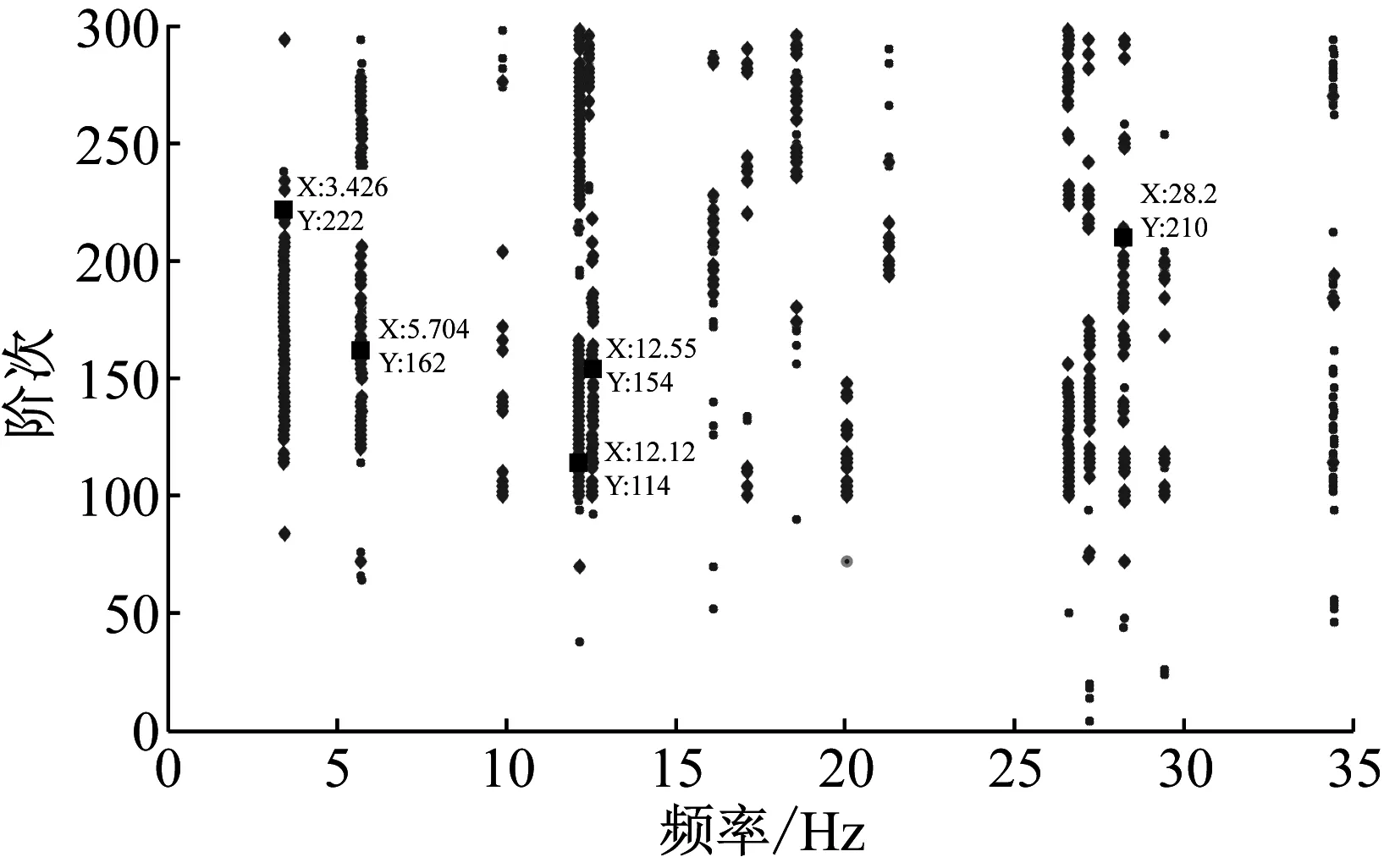
图14 稳定图(EEMD)

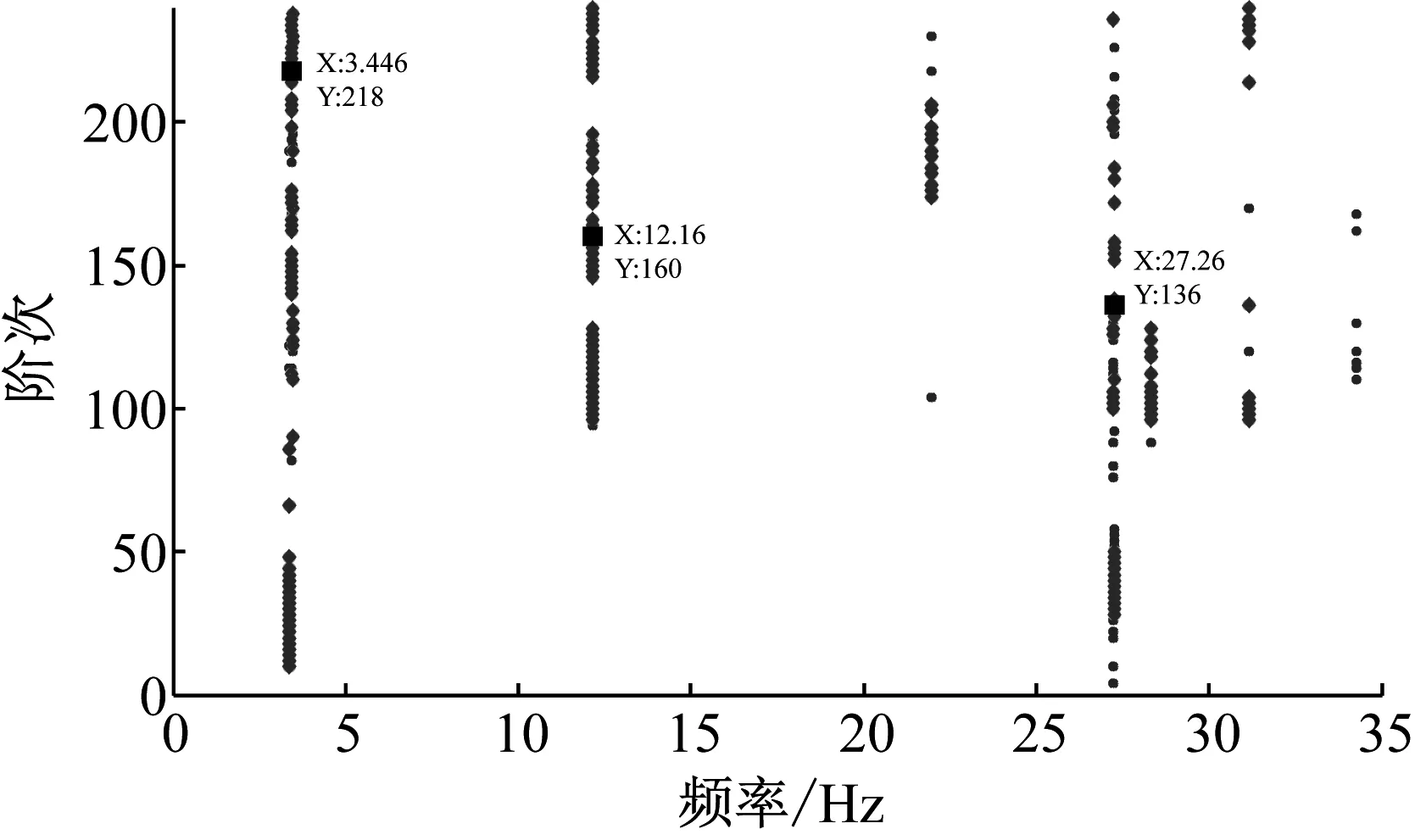
图15 稳定图(改进EEMD)

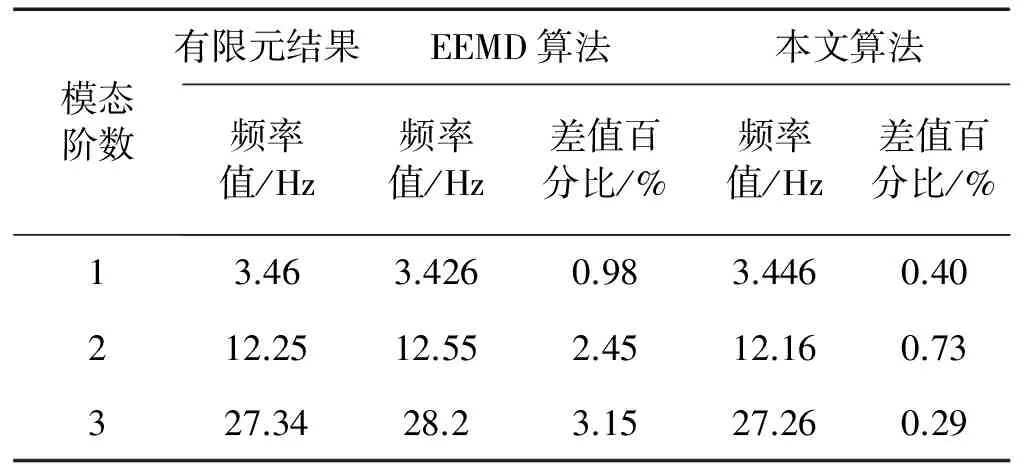
模态阶数有限元结果EEMD算法本文算法频率值/Hz频率值/Hz差值百分比/%频率值/Hz差值百分比/%13．463．4260．983．4460．40212．2512．552．4512．160．73327．3428．23．1527．260．29

利用本文算法预处理该简支梁桥各节点对应的加速度响应信号，再利用随机子空间算法识别预处理后的信号，可得到该简支梁桥前3阶模态振型结果，现将其与理论振型结果进行对比，对比结果见图16所示。

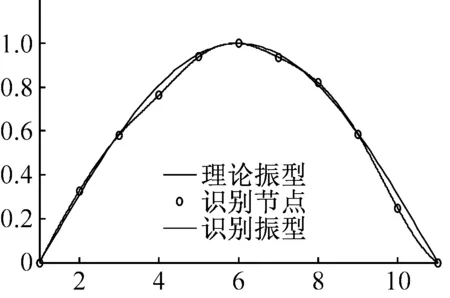
(a) 第1阶振型

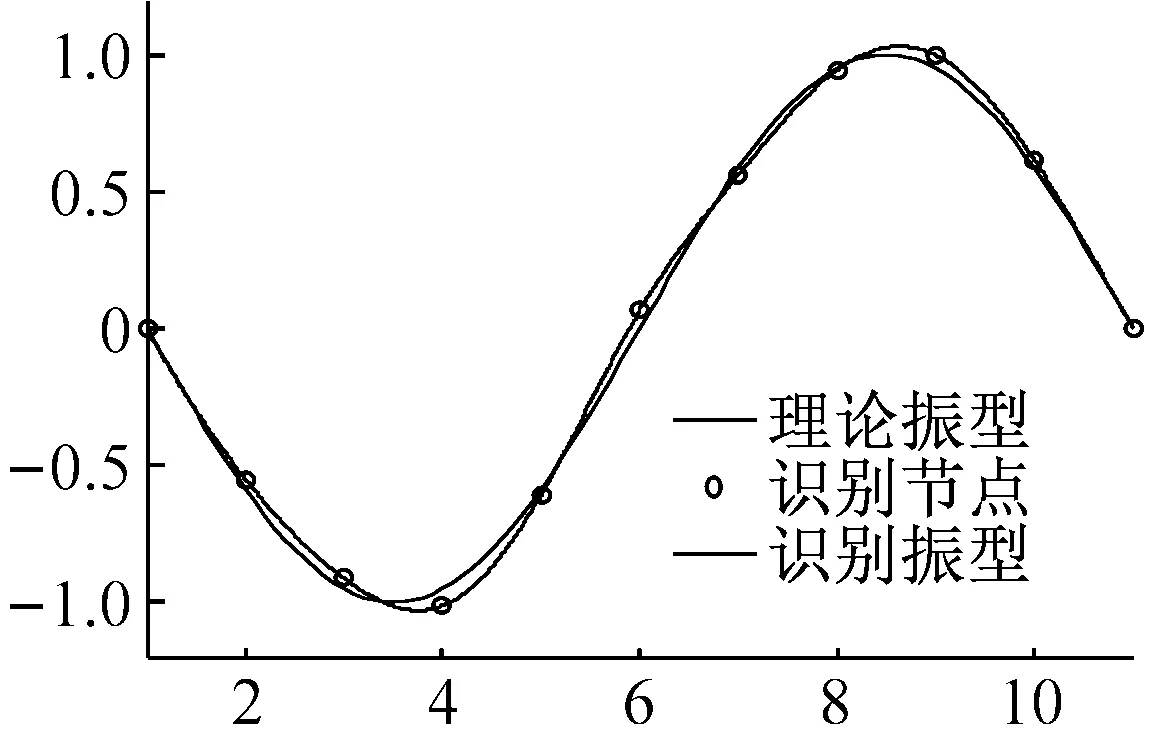
(b) 第2阶振型

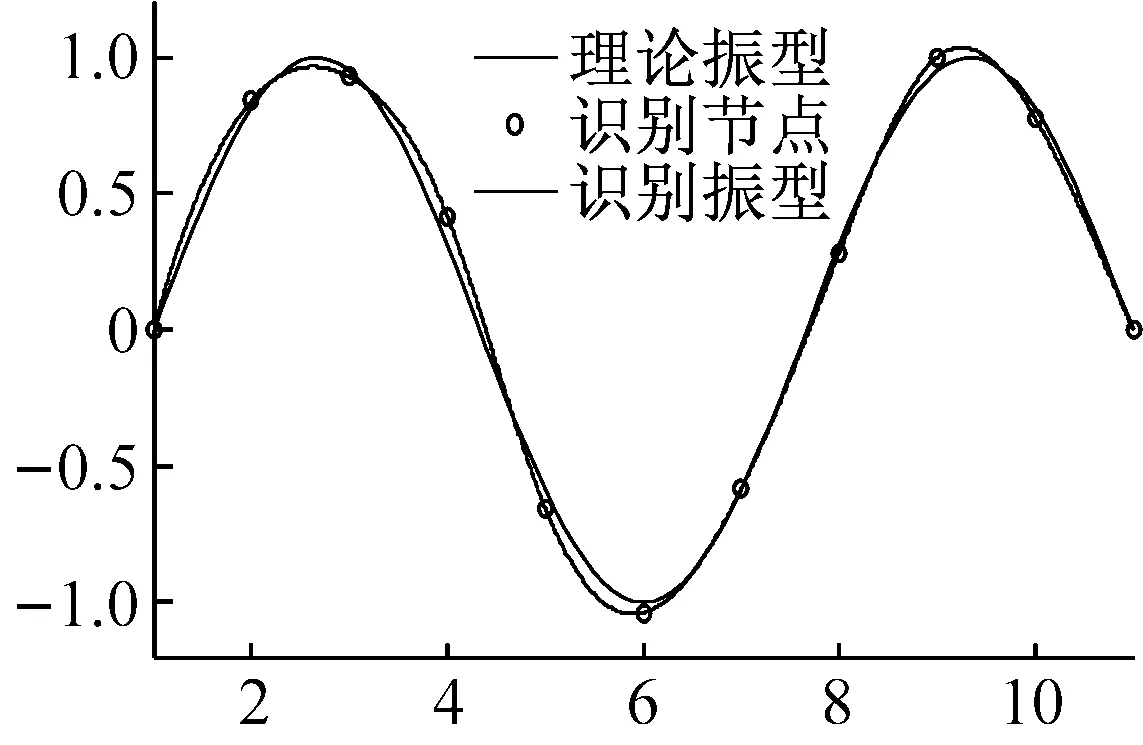
(c) 第3阶振型

通过对比该简支梁桥前3阶模态振型与理论振型之间的差距可知：本文所提改进EEMD算法能运用于桥梁结构信号的降噪处理。

5 结 论

通过将本文算法运用于模拟信号和简支梁桥仿真算例，可得如下结论：

(1) 本文所提的自适应极值点匹配延拓方法能有效改善EEMD算法结果中存在的端点效应问题；

(2) 将聚类分析运用于模态分解过程，能避免所得本征模态函数间的模态混叠现象；

(3) 利用信息熵、能量密度以及平均周期构建的指标-有效程度系数，能实现有效IMF分量的自动筛选；

(4) 简支梁桥仿真算例结果表明，本文提出的改进EEMD算法能运用于桥梁结构响应信号的降噪处理；

综上可知，本文算法相比目前广泛使用的EEMD算法而言，不仅能实现信号的自适应分解与重构，还能更好的对桥梁结构信号进行降噪处理。

[1] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceeding of the Royal Society London A, 1998, 454:903-995.

[2] 张佳文. 基于振动特性的结构损伤识别方法研究[D]. 长沙:长沙理工大学,2009：30-70.

[3] WU Z H,HUANG N E.Ensemble empirical modedecomposition:a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009(10):124-127.

[4] 何星,王宏力,姜伟,等.改进的自适应EEMD方法及其应用[J].系统仿真学报,2014(4):89-94.

HE Xing, WANG Hongli, JIANG Wei, et al. Improved adaptive EEMD method and its Application[J]. Journal of System Simulation, 2014(4):89-94.

[5] 时世晨,单佩韦.基于EEMD的信号处理方法分析和实现[J].现代电子技术, 2011(1):178-184.

SHI Shichen, SHAN Peiwei.Analysis and implementation of signal processing method based on EEMD[J]. Modern Electronic Technology, 2011(1):178-184.

[6] SEKHAR S C, SREENIVAS T V. Novel approach to AM-FM decomposition with applications to speech and music analysis[C]∥International Conference on Acoustics, 2004.

[7] WU F, QU L. An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery[J]. Journal of Sound & Vibration, 2008, 314(3):586-602.

[8] DENG Y. Boundary-processing-techni- que in EMD method and Hil-bert transform[J]. Chinese Science Bulletin, 2001, 46(11):954-960.

[9] 张郁山,梁建文,胡聿贤.应用自回归模型处理EMD方法中的边界问题[J]. 自然科学进展,2003(10):48-53.

ZHANG Yushan, LIANG Jianwen, HU Yuxian. Using autoregressive model processing the boundary problem in the EMD method[J]. Progress in Natural Science, 2003(10):48-53.

[10] CHENG J, YU D, YANG Y. Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform[J]. Mechanical Systems & Signal Processing, 2007, 21(3):1197-1211.

[11] 唐东明. 聚类分析及其应用研究[D].成都:电子科技大学,2010:78-94.

[12] 张超,陈建军. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J].中南大学学报(自然科学版), 2012(3):221-224.

ZHANG Chao,CHEN Jianjun.Gear fault diagnosis method based on EMD energy entropy and SVM-based[J]. Central South University (Natural Science Edition), 2012(3):221-224.

[13] 孙伟峰. 经验模态分解频率分辨率的一种改进方法[J].计算机工程与应用, 2010(1):245-249.

SUN Weifeng.Empirical Mode Decomposition frequency resolution of an improved method[J]. Computer Engineering and Applications, 2010(1):245-249.

[14] 许顺国. 模糊数学综合评判法在水质评价中的应用-以成都市府河为例[J]. 唐山师范学院学报,2007(2):68-70.

XU Shunguo.Application of fuzzy comprehensive evaluation method in water quality evaluation of chengdu fuhe river[J].Journal of Tangshan Normal University, 2007(2):68-70.

[15] 徐士代.环境激励下工程结构模态参数识别[D].南京:东南大学,2006：105-122.

Adaptive Improvement of EEMD algorithm

XU Jian1, ZHOU Zhixiang1, TANG Liang1, RAN Jie2, HE Jie3

(1. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 404100， China;2. Nanchong Municipal Bureau of Housing and Urban Rural Developmen, 637000， China;3. School of Civil Engineering, Southwest Jiao Tong University, 610031, China)

At present, the ensemble empirical mode decomposition (EEMD) algorithm is widely used, but it cannot realize adaptive decomposition and reconstruction of bridge structures’ response signals. Here, aiming at shortcomings of EEMD algorithm, an improved algorithm realizing adaptive decomposition and reconstruction of bridge structures’ response signals was proposed. Firstly, the adaptive extremums matching and extension algorithm was introduced to suppress end effects. Secondly, the decomposed signals were processed with the clustering analysis technique to avoid modal aliasing phenomena. Finally, the corresponding information entropy, energy density and average period of each intrinsic mode function (IMF) were used to construct an index named the effective level coefficient and realize the automatic selection of effective IMF components with this index. The selected effective IMF components were adopted to reconstruct bridge structures’ response signals. The results of simulated signals and a simply supported girder bridge simulation example showed that this proposed algorithm can realize adaptive decomposition and reconstruction of bridge structures’ response signals effectively.

bridge structure; mode decomposition algorithm; end effect; clustering analysis; signal reconstruction

国家自然科学基金(11627802;51478071)

2016-05-20 修改稿收到日期：2016-09-05

徐健 男，博士生，1987年生

周志祥 男，博士,教授,1958年生 E-mail：2252666725@qq.com

U446.3

A

10.13465/j.cnki.jvs.2017.11.034