空间想象与构造图形交替思维——几则空间想象能力的考查到了极致的关于球的立几题

云南省玉溪第一中学(653100) 武增明

空间想象与构造图形交替思维
——几则空间想象能力的考查到了极致的关于球的立几题

云南省玉溪第一中学(653100) 武增明

在高考、竞赛中,经常出现短小精悍、新颖别致、设计独特、能力立意高、很灵活的关于球的立几小题,以考查同学们的空间想象能力和构造图形的能力,可以说达到淋漓尽致的程度.现采撷几例加以分析,以期对提高同学们的空间想象能力和构造图形的能力有所帮助,同时也供同仁教学参考.

例1 (2011年全国卷II理科11(文12)题)已知平面α截一球面得圆M,过圆心M且与α成60°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )

A. 7πB. 9πC. 11πD. 13π

解设球面的球心为O,圆M和圆N的公共弦为BC.过点M作AM⊥BC,因为MO,MN,MA都垂直BC,所以MO,MN,MA共面.因为∠NMA=60°,∠OMA=90°,所以∠OMN=30°,如图1.在Rt△OMC中,

图1

评注(1)通过空间想象,画出符合题意的示意图,是快速破解此题的一个重要关键.(2)圆N的劣弧BC在球面内,但这与解答此题无关.

例2 已知球O的半径为2,圆O1,O2,O3为球O的三个小圆,其半径分别为若三个小圆所在的平面两两垂直且公共点为P,则OP=____.

图2

评注(1)此题中的点P在球O面外.(2)此题要求我们要有较强的空间想象能力,这样才能把立体图呈现在头脑中,由此并画出相应的立体图,进而得以获解.(3)要直接画出立体实图,困难很大.

例3 在一个棱长为6的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,则该纸盒内正方体棱长的最大值是___.

分析此题若直接求解,困难非常大,若借助正四面体的内切球来解答,会收到意想不到的效果.其思路是,先求出正面体的内切球的半径,然后再求球的内接正方体的棱长,这时的正方体的棱长最长,即为盒内正方体棱长的最大值.

解设正四面体各面的面积为S,高为h,其内切球的半径为R,则由三棱锥的等体积法得,

设此正四面体内切球的内接正方体的棱长为a,则即纸盒内正方体棱长的最大值是

评注(1)想到正四面体内切球的内接正方体的棱长最长,是破解此题的关键.(2)解答完此题后,我们更进一步掌握球内接的长方体或正方体在其球内可以任意转动.

例4(2010年全国高中数学联赛新疆维吾尔自治区预赛试题)已知半径为r的球和半径为R的两个相切的球都相切,且它们都与大小为60°的二面角的两个半平面相切,则

解析设半径为R的两个球的球心为O1,O2,半径为r的球的球心为O3,通过空间想象,把符合题设的立体图呈现在脑海中,由此画出简要的立体图,如图3.依题意知,点O1,O2,O3确定的平面平分已知二面角,且点O1,O2,O3到二面角的距离分别为2R,2R,2r.过点O3作O3H⊥O1O2,垂足为H,则O3H=2R−2r,O1O3=O2O3=R+r.所以O1H=HO2=R.在Rt△O1HO3中,

图3

评注要把符合题意的立体图全部画出来,困难是巨大的,也没有这个必要.

在立体几何学习中,需要我们有较好的空间想象能力,这样我们才能把立体图呈现在头脑中,进而画出简要的立体图或详细完整的立体图,才有可能获解.简单地说,解决型如上面所例举到的那类问题的有效思维途径是空间想象与构造图形交替思维.

例5 棱长为2的正方体ABCD−A1B1C1D1的所有顶点均在球O的球面上,E,F,G分别为AB,AD,AA1的中点,则平面EFG截球O所得圆的半径为____.

图4

图5

解析设球O的半径为R,则依题意得(2R)2= 22+22+22⇒R2=3.

评注(1)要把符合题意的立体图全部画出来,困难是很大的,也没有这个必要.(2)在解答此题时,需要一半空间想象一半画图.(3)在解答此题时,要想到平面EFG截球O所得圆与等边三角形EFG的外接圆是同心圆.

例6 三个半径都是1的球放在一个圆柱内,每个球都接触到圆柱的底,则圆柱的底面圆半径的最小值是( )

解析问题可转化为,三个半径都是1的小圆放在一个大圆内,三个小圆两两外切,求大圆半径的最小值.

当且仅当三个小圆两两外切,且与大圆内切时,大圆半径最小,设此时大圆的半径为R.设三个球的球心分别为O1,O2,O3,即三个小圆的圆心分别为O1,O2,O3,设大圆的圆心为O,如图6.大圆的圆心O是等边三角形O1O2O3的外心(“四心”重合),于是故选A.

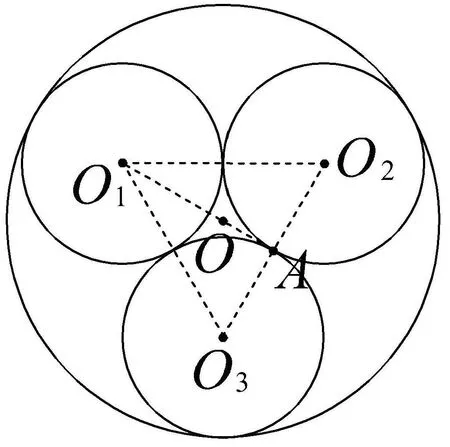
图6

评注(1)要把立体图画出来,很难,也没有这个必要.(2)解答此题时,关键是通过空间想象后把问题作等价转化.

例7 (2016年高考全国卷III文科11(理科10))在封闭的直三棱柱ABC−A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )

解析首先考虑球与封闭的直三棱柱ABC−A1B1C1的三个侧面相切,此时球的半径R等于直角三角形A1B1C1的内切圆的半径,如图7,这时R=2.而AA1=3,因此,若R=2,则封闭的三棱柱ABC−A1B1C1容纳不下球,从而考虑球与封闭的三棱柱ABC−A1B1C1的两底面都相切,此时球的半径R最大为这时球的体积为故选B.

图7