三次多项式的对称点及其应用
——从广州一模的一道选择题谈起
2017-06-15华南师范大学数学科学学院510631尹淑芬
华南师范大学数学科学学院(510631) 尹淑芬
三次多项式的对称点及其应用
——从广州一模的一道选择题谈起
华南师范大学数学科学学院(510631) 尹淑芬

处理这道题的关键一步是要找到这个三次函数所对应的三次多项式的对称点,接着利用三次多项式对称点的定义与性质进行计算.其实三次多项式的对称点在高中解题中有比较大的应用.因此笔者就写下本文了.笔者将在本文先证明三次多项式ax3+bx2+cx+d(a≠0)的对称点的存在性,接着给出三次多项式关于对称点的性质,最后举例说明这些性质在解题中的应用.
三次多项式的对称点的概念界定
对于三次多项式ax3+bx2+cx+d(a≠0),如果存在某一实数x0,对任意x都有成立,就称x0为此三次多项式的对称点.例如,三次多项式x3−3x2+2x+1,实数1满足(1−x)3−3(1−x)2+2(1−x)+ (1+x)3−3(1+x)2+2(1+x)=2×13+2×(−3)×12+2×1×1,那么实数1就是三次多项式x3−3x2+2x+1的对称点.
附注如果实数x0是三次多项式的对称点,那么有

三次多项式的对称点的存在性


证明3 不难发现三次函数的对称中心的横坐标就是三次函数所对应的三次多项式的对称点,观察三次多项式ax3+bx2+cx+d(a≠0)所对应的三次函数f(x)=ax3+bx2+cx+d(a≠0)的图像,可以知道函数图像在对称中心左右两边的凹凸性是相反的,如果a>0,函数在对称中心的左边是凸函数,随着自变量x的增大,切线的斜率在减小,三次函数的二阶导数小于0,而在对称中心的右边是凹函数,随着自变量的增大,切线的斜率在增大,三次函数的二阶导数大于0;如果a<0,函数在对称中心的左边是凹函数,随着自变量x的增大,切线的斜率在增大,三次函数的二阶导数大于0,而在对称中心的右边是凸函数,随着自变量x的增大,切线的斜率在减小,三次函数的二阶导数f′′(x)小于0.不难发现,三次函数的二阶导数在对称中心处等于0.因此要求三次多项式ax3+bx2+cx+d(a≠0)的对称点可以求出三次函数f(x)=ax3+bx2+cx+d(a≠0)的二阶导数f′′(x)的零点,该零点就是三次多项式的对称点.
从上述证明过程,可以得知任何三次多项式ax3+bx2+cx+d(a≠0)存在唯一对称点
三次多项式的对称点的性质
从上述证明过程,可以获得三次多项式的对称点的如下性质:
性质一三次多项式ax3+bx2+cx+d(a≠0)的对称点是三次函数f(x)=ax3+bx2+cx+d(a≠0)二阶导数f′′(x)=6ax+2b的零点.
性质二三次多项式ax3+bx2+cx+d(a≠0)的对称点是三次函数f(x)=ax3+bx2+cx+d(a≠0)一阶导数f′(x)=3ax2+2bx+c的对称轴

三次多项式的对称点在解题中的应用
例1(2013年高考全国2卷文科、理科数学第10题)已知函数f(x)=x3+ax2+bx+c,下列结论错误的是( )
A.∃x0∈R,f(x0)=0
B.函数y=f(x)的图像是中心对称图形
C.若x0是f(x)的极小值点,则f(x)在区间(−∞,x0)上单调递减
D.若x0是f(x)的极小值点,则f′(x0)=0

例3(湖北省八校2016届高三联考第12题)已知直线x−9y−8=0与曲线C:y=x3−px2+3x相交于点A,B,且曲线C在A,B处的切线平行,则实数p的值为( )
A.4 B. 4或−3 C.−3或−1 D.−3
解析(常规方法)由y=x3−px2+3x,得y′= 3x2−2px+3.设A(x1,y1),B(x2,y2),则曲线C在A,B处的切线的斜率分别为
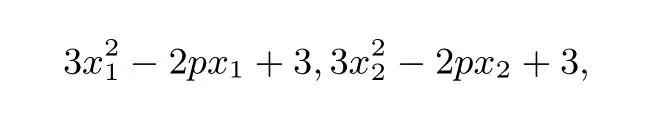
因为曲线C在A,B处的切线平行,所以


新方法因为曲线C在A,B处的切线平行,所以直线过曲线C的对称中心所以p=−3或p=−1或p=4.当p=−1,y′=3x2+2x+3>0,曲线C单调递增,与直线x−9y−8=0相交于一点,因此p≠1.经检验,p=−1与p=4符合题意.
评注显然,常规方法计算量大,运算繁琐.然而利用三次多项式的对称点的性质就能简单快捷地解答本道题,而且也容易理解.
例4 (2004年高考重庆理科数学卷第20题)设函数f(x)=x(x−1)(x−a),(a>1)
(1)求f′(x);并证明f(x)有两不同的极值点x1,x2;
(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范围.

评注利用三次多项式的对称点的性质进行解答问题(2),解答过程简短,思路清晰.也省去了常规方法中的繁琐的运算.
从上述例题,可以发现三次多项式的对称点在高考中还是比较常见的,而且利用其性质解题能够简化计算,也更加便捷,因此考生应给予必要的重视,将它的性质应用于解题中.
