新课标高考数学客观题的考点分布及解法探析

宁夏回族自治区固原市第二中学(756000) 张兴

宁夏回族自治区固原市回民中学(756000) 李雪琴

新课标高考数学客观题的考点分布及解法探析

宁夏回族自治区固原市第二中学(756000) 张兴

宁夏回族自治区固原市回民中学(756000) 李雪琴

高考数学选择题为考查“四基”的小型综合题,其解答的效益、效果和效率,对考试成败起着决定性的作用,通过对历年考试题及其解答的统计分析,得出解答数学选择题有数学计算性、数形结合性和数学分析性三大策略.

选择题;解答方法;突破策略

高考数学试题多,考查面广,不仅要求答题的准确率,还要求有较快的解题时速度,由于选择题排布在最前面,占总题数的60%,为考查“四基”的小型综合题,所以选择题解答效益、效果和效率决定了做题能否进入最佳状态,对考试的成败起着决定性的作用,因此研究解答题的突破策略,具有很重要的现实意义.

一、数学计算性求解策略

数学计算求解就是直接从题设条件出发,运用有关概念、性质、定理、法则等,通过严密的推理和准确的运算,得出正确结论的方法.从2007年到2016年新课标文理共30套题中,必须通过数学计算才能解答的选择题目有“七算”,其中集合运算25个、复数运算28个、框图流程运算30个、函数与导数运算11个、三角运算24个、数列运算14个、向量运算17个、概率计算13个.平均每套题5个,占选择题的40%,说明数学计算是求解选择题最基础的方法.

例1(2013年1卷理科第1题)已知集合A={x|x2−2x＞0},B={x|−5＜x＜5},则( )

A.A∩B=∅ B.A∪B=R

C.B⊆AD.A⊆B

解析A={x|x2−2x＞0}={x|x＜0或x＞2}所以A∪B=R,故选B.

例2(2013年1卷理2题)若复数z满足(3−4i)z= |4+3i|,则z的虚部为( )

解析由(−4,−3),A(0,1),得 点C(−4,−2),则(−4−3,−2−2) = (−7,−4),选A.

例6 (2010年 文8题)如果执行右面的框图,输入N= 5,则输出的数等于 ( )

图1

解析根据框图运行计算,得答案为D.

例7 (2016年 理 II卷 10题)从区间[0,1]随 机 抽 取 2n个 数x1,x2,···,xn,y1,y2,···,yn,构成n个数对 (x1,y1),(x2,y2),···,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )

图2

解析由题意得(xi,yi)(i=1,2,···,n)在如图所示方格中,而平方和小于1的点均在如图所示的阴影中.由几何概型概率计算公式知选C.

上面七个例题代表七类运算,它们分别是集合运算、复数运算、框图流程运算、函数与导数运算、三角运算、数列运算和概率运算.第一,它们基本都排在12个选择题的前面,属于简单易做的题目,是高考保证分值的部分.第二,它们的内容都是针对四基,即基础知识、基本技能、基本思想和基本活动经验.第三,解答这些题目,首先要掌握七类运算各自独特的算理和算法.其次强化对四基的理解和运用.再次要保持信心、认真审题和细致解答.

二、数形结合求解策略

数形结合就是根据题目条件,做出所研究代数问题的几何图形,或者把几何关系转化为代数关系,解决问题的办法.从2007年到2016年新课标文理共30套题中,通过数形结合解答的选择题主要有“六图”,即函数零点与图像22个、三角函数图像18个、圆锥曲线的图像30个、平面区域图像14个、三视图26个、球与多面体的组合体19个.平均每套题4个,占总数的三分之一.说明数形结合是解答选择题最重要的方法.

例8(2011年文2)已知函数y=f(x)周期为2,当x∈[−1,1]时f(x)=x2,那么函数y=f(x)的图像与函数y=|lgx|的图像的交点共有( )

图3

A. 10个 B. 9个 C. 8个 D. 1个

解析做出如上的图像,由图像知选择A.

例9(2016年文II卷3题)函数y=Asin(ωx+φ)的部分图像如图所示,则( ).

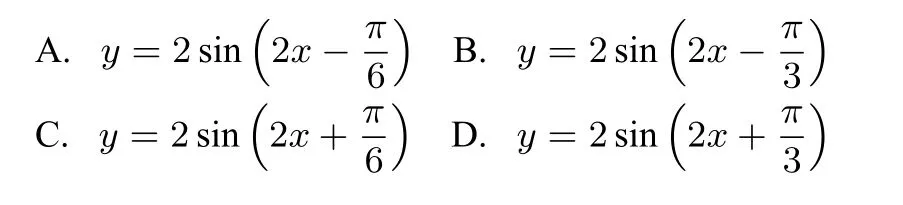
图4

例10(2015年理 II卷 11题)已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为( )

图5

图6

解析当目标函数经过A点时取得最小值,而A(1,−2a),所以2−2a=1,得

例12(2012文7题)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( ).

A.6B.9C.12D.18

图7

解析由俯视图知此几何体的底面为等腰三角形,且一边长为6,其上高为3,由正视图与此视图知有一个侧面垂直于底面,且高为3,可以计算出体积为9,故选择B.

例13(2016理III卷10)在封闭的直三棱柱ABC−A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )

上述六个例题,分别代表函数零点与图像、三角函数图像、圆锥曲线图像、平面区域图像、三视图、球的组合体六个方面的图像问题.其中三角函数图像主要涉计由解析式做出图像、根据图像求解析式、图像的平移以及对称性等.平面区域图像问题即线性规划,主要涉及求二元函数的最值、由最值求某个参数值等.三视图主要涉及把三视图还原为直观图,再求体积或面积.这三个相对比较容易解答.剩下的球与多面体的组合关键在于图像分解,特别要注意交点和切点的运用.圆锥曲线的图像理科以双曲线为主,文科以抛物线为主,主要考查定义和性质.函数的零点与图像,主要涉及指数、对数、二次和分段这几类函数的图像交点问题.这三个相对有一定的难度,解答时关键要抓住图像特征,从图像中寻找解题的切入点,尤其要重视课本中相关的典型题目.

三、数学分析求解策略

数学选择题不仅告诉已知条件,需要回答什么问题,同时还将正确答案隐藏在试题“四选一”选择支中,由于有备选项,给试题的解答提供了丰富的信息,使得数学分析求解策略成为一种特色.所谓数学分析求解就是指通过数值分析、图像分析、性质分析、代入分析和逻辑分析求解问题的办法.从对历年的高考试题统计可以看出,每年有三个左右可以使用此方法解答,其中至少有一个必须使用,而且解答难度比较大的题目,通常会有意想不到的效果.

例15(2016理I卷7题)函数y=2x2–e|x|在[–2,2]的图像大致为( )

图8

解析当x=2时,y=2x2–e|x|=2×22−e2＞0,且y＜0,故排除A、B,令x→0+,y′=4x−ex＜0,y=2x2–e|x|为减函数,排除C.

例16(2016文II卷10题)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是( ).

A.y=xB.y=lgxC.y=2xD.

解析y=10lgx的定义域和值域都是正实数,四个备选答案中适合条件的只有D.

例17(2016理I卷8题)若a＞b＞1,0＜c＜1,则( ).

A.ac＜bcB.abc＜bac

C.alogbc＜blogacD. logac＜logbc

解析若ac＜bc,又c＞0⇒a＜b,与已知a＞b＞1,0＜c＜1矛盾,故排除A.若abc＜bac⇒ac−1＞bc−1,又c−1＜0⇒a＜b,与已知矛盾,故排除B.若logac＜logbc⇒⇒logca＞logcb⇒ac＞bc,故排除D.

例18关于a,b正确的选项( )

A. |a|＜1或|b|＜1 B. |a|＜1且|b|＜1

C. |a+b|＜|1+ab| D. |a|＜1且|b|＜1

解析若B为真,即|a|＞1且|b|＞1⇒(a2−1)(b2−1)＞0⇒(1+ab)2＞(a+b)2⇒|1+ab|＜|a+b|;所以B, C同真,故排除B.

若C为真,即|a+b|＜|1+ab|⇔(a+b)2＜(1+ab)2⇔(a2−1)(b2−1)＞0.又由于B不真,故|a|＜1且|b|＜1,由于以上每一步都可逆,于是C,D同真,故排除C,D.故选择A.

上述5个例题的解答分别代表数值分析、图像分析、性质分析、代入分析和逻辑分析.其中数值分析就是分析题目中的数值及其变化趋势,从中探究结果.例14的解法一为常规解答,综合使用了计算和数形结合的手段,解法二采用数值分析,先分析特殊值的特征,再分析数值变化中的特征,很明显方法二优于方法一.图像分析就是分析特殊点、特殊图形以及图形变化过程中探究结果,即例15的解法.性质分析就是分析题目给出条件,所具有的一些特殊性质,即例16的解法.代入分析就是指把条件代入选择支进行检验,或者把选择支代入条件进行检验,排除不适合的选项,进而得出正确选项的方法,即例17的解法.逻辑分析就是利用逻辑知识,分析四个选择支相互之间关系,排除不符合逻辑的选项,确定答案的办法,即例18的解法.

通过上文的探究我们就会发现,解答数学选择题有数学计算性、数形结合性和数学分析性三大策略,其中数学计算是基础性策略,主要用于解答排列在选择题前面的“七算”问题,只需要掌握七类运算的算法和算理.数形结合是提高性策略,主要用于解答排列在选择题后面部分的“六图”问题,关键要在图像特征中寻求解题切入点.而数学分析则是前两种策略的有效补充,运用恰当,可以起到四两拨千金的效果.