把握中考方向 备考有的放矢

李玉奎

[摘 要] 本文对初三数学总复习的相关策略进行详细分析和研究，从根本上保证初三学生的数学成绩能够有所提升，取得满意的成绩.

[关键词] 初三数学；总复习；策略；提高

中学总复习是学生备战中考非常重要的一个阶段，如何提升总复习的课堂教学质量和效率，是每一个毕业班教师所面临的严峻問题. 教师在针对初三数学总复习采取有效措施的时候，要与学生的实际情况进行有效结合，采取有针对性的复习方案，让学生能够在短时间内对初中三年所学到的知识进行一个系统性的回忆和复习，逐渐形成一个完整的数学知识体系. 这样不仅能保证学生很好地解决数学习题，而且能迅速提高数学成绩，促使学生在中考中取得优异的成绩.

明确中考方向

中考方向现如今在社会经济以及教育行业的不断发展和变化形势下，同样发生了重大变化. 当前中考方向已经逐渐倾向于学生的素质教育，这种素质不仅包括对学生的人性教育，而且要让学生具备全面的知识结构体系，能够利用理论知识解决一些实践性的问题，从根本上保证学生问题观察、问题解决、问题处理以及想象能力的提升. 中考试卷已经逐渐打破传统试卷的局限性，更加注重对学生能力水平的检测，虽然题目很容易让学生看懂，但是越往下答题，就会发现题目的形式以及内容深度越复杂，所考验学生的知识和能力也越全面.

初中数学总复习中教师的困惑

初中数学总复习阶段，时间非常紧迫，但是复习任务却非常繁重，无论是对学生还是教师来说，要求都非常高. 在这种形势下，教师难免会出现一些问题或者困惑，这主要体现在下面几个方面. 首先，在中考过程中，不同的数学习题在解题书写格式上如何做到规范化的解答. 其次，复习范围的实际难度要怎样科学合理地把控，才能让学生全面复习所学知识，帮助学生建立良好的知识体系结构. 最后是学生的现状. 由于学生自身存在一定的差异性，在复习当中这种差异性也比较明显，教师如何针对学生的不同特质实施有效复习等. 这些问题是在初三数学总复习中，数学老师所面临的困惑，更重要的一点是，如何在短时间内将学生的数学成绩进行普遍性地提升，这些问题都需要教师在日常教学中着重思考.

2016年成都中考试题的变化

2016年成都市的中考分值为150分. 2016年成都中考数学试题对实践性比较强的知识加大了难度，特别是角、圆以及一些公式、方法的应用，A卷第20题考查圆，第27题考查四边形. 一些比较复杂的大题都相对地缩减了，主要是为了检验学生知识体系构成的全面性.

中考评价体系

中考评价体系是国家宏观的一种对中考情况进行指导、控制以及评价的有效措施，同时也是中考活动自身科学化、规范化的一种表现形式. 中考评价体系的构成和实施，不仅是为了保证基础教育质量的整体水平和标准能够达到一定的要求，而且能够从根本上保证中考活动的整体效率和效益，为社会日后的发展提供更多标准型的人才.

复习策略及建议

1. 制定切实有效的复习计划

从中考数学考试说明的内容可以看出，初中数学包含的知识点非常多，如果只是单纯地依靠教师的复习讲解，很容易导致学生出现混淆的现象. 因此，制定切实有效的复习计划非常有必要. 中考总复习本身就是在时间非常紧迫的环境下，将更多的知识和内容进行反复推敲和深入，所以，在这种形势下，只有保证按照教师制定的复习计划逐渐加深难度，才能促使初中数学知识的系统性充分发挥. 针对初三学生进行数学总复习训练时，要引导学生自己制定符合自己实际情况的复习计划和知识体系，让学生能够逐渐养成良好的问题解决意识，通过自己的实践和深入挖掘，能够解决一些问题. 这样不仅能让学生逐渐意识到中考数学的整体命题方向，而且能强化学生的知识记忆，让学生举一反三，碰到类似问题时，也能迎刃而解.

2. 注重习题归类训练

当前，在初中数学总复习当中，传统模式下的“题海式”战术仍然存在，很多学生每天都忙着做各种各样的习题，很多教师只注重学生在习题解答过程中的数量，并没有注重习题解决的质量. 很多学生只知道解题，并没有对问题进行总结和分析，再次遇到类似问题时，仍然使用“死记硬背”的方式方法进行解答. 这样不仅会造成学生的心理负担，而且效果并不是很理想. 所以，教师要引导学生注重习题归类，让学生对同类型习题进行总结，这样不仅能培养学生的随机应变能力，而且能从根本上提高学生自身的数学解题技巧，帮助学生在中考中取得较好的成绩.

3. 例题讲解要注重变化拓展

对于毕业班的学生来说，在数学总复习的时候，例题是最具代表性的习题，也是最能说明问题和体现解题思路以及方式方法的习题. 所以在总复习时，教师要有意识、有目的地在例题的基础上进行知识习题的延伸和变化，对问题进行深入挖掘和分析，让学生能够在习题的变化过程中，不仅能巩固知识，而且能发散思维，找到问题之间的规律，达到良好的解题效果.

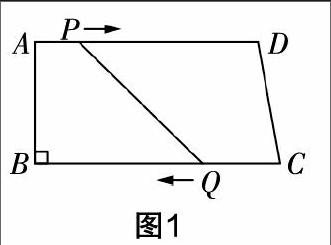
比如，在对四边形内容进行复习的时候，可以根据习题的变化形式让学生领悟到更多同类题型的变化，让学生举一反三. 如图1，四边形ABCD是直角梯形，∠B=90°，AB=8 cm，AD=24 cm，BC=26 cm，点P从点A出发，以1 cm/s的速度向点D运动. 同时，点Q从点C同时出发，以3 cm/s的速度向点B运动，其中一个动点到达端点的时候，另外一个动点也随之停止运动. 在这种形势下，如果从运动开始计算的话，经过多少时间之后，四边形PQCD能成为平行四边形？能成为等腰梯形？

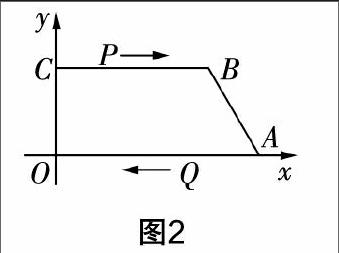
变式1 如图2，四边形OABC是直角梯形，边OA，OC分别在x轴和y轴上，OA=36 cm，OC=14 cm，BC=22 cm，点P从点C出发，以2 cm/s的速度沿着折线C-B-A向点A运动. 同时，点Q从点A出发，以3 cm/s的速度向点O运动，其中一个动点到达终点之后，另外一个动点也随之停止运动.

（1）求经过多少时间，四边形PQAB是平行四边形；

（2）求四边形PQAB是等腰梯形时，点P的坐标.

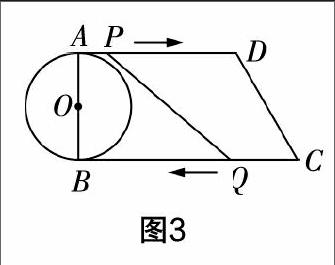
变式2 如图3，圆O的直径AB=4，四边形ABCD是直角梯形，AD∥BC，∠B=90°，AD=6，BC=8，点P从点A出发，以每秒1个单位长度的速度向点D运动. 同时，点Q从点C出发，以每秒2个单位长度的速度向点B运动，其中一个动点到达终点，则另一个动点也随之停止运动. 假设点P运动的时间为t秒.

（1）求CD的长；

（2）当t为多少时，四边形PQCD是等腰梯形？

从上述两个变式题可以看出，在条件不断变化的情况下，学生不能利用原题的解题思路以及方式方法进行解答. 这样的习题变化形式，不仅能从根本上将学生的思路打开，而且能培养学生举一反三的能力，让学生从不同的思考角度对问题进行分析. 这样不仅能改变学生机械式的模仿练习，而且能让学生逐渐学会如何对问题进行分析和研究，如何根据问题的已知条件，找出最佳解决问题的路径和方式方法. 在数学例题的不断变化当中，学生不仅能对知识进行巩固，而且能在点运动的过程中寻找其自身的数学变化规律.

对于初三的学生来说，数学总复习一直都很重要，单纯地按照传统复习方式将例题进行统一讲解，很容易导致学生在学习的过程中出现注意力不集中或没有兴趣的现象. 这样学生不仅自身的解题能力得不到训练，而且总复习的效果也不能达到良好的状态. 因此，教师要在例题的讲解过程中善于变化、拓展，要将学生的潜能充分挖掘出来. 在对例题进行分析和解答的过程中，不仅要将例题自身的作用发挥出来，而且要让学生根据一道例题的分析和学习，解答出与之相关的其他题目，这样学生就能在初中数学复习知识的过程中将知识之间的纵横联系进行有效连接，帮助学生建立良好的知识网络体系，还能将学生的解题思维以及思考模式充分发散，提高学生灵活解题的技巧和能力.

综上所述，在初三数学总复习过程中，无论是教师还是学生，都面临着巨大的压力，在短时间内要将初中三年所学到的知识进行系统性地复习，需要师生的共同努力. 教师要培养学生良好的解题思维，打破传统解题模式中的局限性，锻炼学生善于归纳和总结的能力，从而提高学生的数学成绩.