高中数学中的立体几何解题技巧
2017-06-13筅江苏省宜兴中学石琳
筅江苏省宜兴中学石琳
高中数学中的立体几何解题技巧
筅江苏省宜兴中学石琳
对于我们这些高中的学子来说,面临着即将到来的高考.高考是我们人生中一个巨大的转折点,在一定程度上决定着我们以后的命运及生活的优劣,因此,我们一定要花费百倍努力在高考的平台上打一个漂亮的胜利仗,完美地发挥出我们自身的潜力,不让之前的努力成为无用功,让社会认识到我们自身的价值.在高考的备考中,数学是一门非常重要的课程,但是由于高考出题人的出题技术非常的高超,我们要灵活地运用所学到的数学知识进行解答.本文将以高中数学中的立体几何解题技巧为主题进行详细的讨论和分析,介绍如何进行高效的数学备考.
一、熟练掌握立体几何的数学知识
如果只是讨论数学立体几何的知识,并不是特别的复杂,但是如果将其他数学知识与几何问题相结合,我们所要学习的知识就会几何式的增加.所以,我们要首先进行立体几何知识的熟练掌握,然后不断了解这些知识之间的联系,不断建立出一个完整的立体几何知识结构,便于之后的复习和提高,最后,我们要不断掌握其他数学知识与立体几何相结合的解题技巧.我们通过不断进行知识的积累和掌握知识之间的联系,不断在立体几何习题中熟练运用所学的知识.下面对相关的立体几何知识进行简单的总结和分析.第一,在理解的情况下进行相关定义的掌握.在立体几何的习题中,我们经常看见一些比较特殊的空间几何体,如果我们对其主要的定义都不了解,更别说运用其相关性质进行解答了.比如,直棱锥是侧棱与底面垂直的特殊几何体,正棱柱是底面为正多边形的直棱柱,正棱锥是底面为正多边形,顶点在底面的投影为底面多边形的中心,正四面体是四个面都是正三角形的几何体,正三棱锥是底面为正三角形,侧面为等腰三角形的几何体等.我们在学习这些特殊的几何体时,不要死记硬背,要找到其中的共同点,在理解的基础上进行记忆,便于以后我们在习题中熟练运用.另外,我们要对相关知识的解题方法进行熟练的运用.
比如,在几何大题中经常出现的线线角、线面角、面面角的求解方法.下面对其中的线面角进行简单的分析.首先,我们要了解线面角的范围,避免在进行解答的时候出现两个答案,造成解题的错误.其次,我们要熟记面面角的解题公式.线面角的求解方法主要有两种,一种是通过向量的方法进行建立三维直角坐标系,将所需要的线段用向量的方法进行表示出来,然后通过线面角的求解方法和向量法的化简技巧进行解答,这种解题方法是比较简单的,容易进行理解和解答,但是解题的过程比较烦琐,会花费大量的做题时间.如果这是一道三问的大题,下面的几问也可以运用向量的方法进行解答.另一种就是通过我们的立体几何思维,找出其中的相关联系,不断进行所需要的线段长度,运用面面角的求解公式进行解答.这种求解方法对我们的思维有一定的要求,不然很容易出错.这两种的解题方法我们都要有所掌握,对于一些简单的面面角求解采用第二种方法进行解答,节约高考中宝贵的时间.最后,我们还要对相关的方程进行记忆,比如椭圆的轨迹方程,抛物线的轨迹方程等.总而言之,通过我们不断进行相关立体几何知识的积累和思考其中的联系,逐渐熟练掌握并能够加以运用,构建出适合自己的知识结构框架,为立体几何的解题打下夯实的基础.
二、培养提高立体几何的思维空间
对于高中数学立体几何知识的学习中,我们空间思维的建立是非常重要的,通过我们的思维空间能够快速地了解题目中相关题干,便于解题时的运用,另外,我们也能够通过相关空间解题方法在原立体几何中添加合适的辅助线,来帮助我们清楚求解的目标.我们思维空间的建立,并不是通过知识的学习就能够掌握的,需要我们通过对事物的观察和思考.下面具体介绍如何在立体几何解题中来提高自己的思维空间.在我们进行立体几何习题的解答中,经常遇到在一些对特殊几何体进行计算的习题,题干中会给我们一些立体几何的图形.当我们的思维空间能力不强的时候,很难从中找到相应的解题方法.这个时候我们可以通过手工来自己制作一个简易的立体几何图形,来帮助我们进行解答,同时不断培养和提高自己的思维空间.在我们进行制作简易图形中也可以不断加强对特殊立体几何性质的记忆,另外,在进行这样的立体几何解题中,所给出的图形并不适合我们的直接观察,可以将制作出的简易图形进行翻转,能够直观地观察到线段之间的联系,来帮助理解和解答.最后,我们可以通过相关的多媒体设备进行培养和提高自己的思维空间.通过互联网我们可以找到一些立体几何图形翻转的视频或者动态图,在观察中不断建立自己的思维空间.通过运用互联网和相关的多媒体设备,以及自己制作相关的立体几何简易图形,来不断建立自己的思维空间,进行发散思维思考和仔细的观察,进一步提高自己的思维空间.
三、大量丰富立体几何的练习解答
对于我们高中生来说,都非常清楚地知道数学的学习和提高,离不开大量的数学习题训练,当然立体几何知识的学习也不例外.大量练习题的训练是必可少的,但是我们要保证训练的高效性,不能只是为了完成大量的训练,我们要从大量的习题中总结相应的方法,来不断提高自己的解题能力.下面介绍几道立体几何的习题来进行详细的分析.比如下面这道立体几何的证明题.题目是这样的,如图1,已知正四棱柱ABCD-A′B′C′D′的底边边长为3,侧棱长为4,连接A′B,过点A作AF垂直于A′B,垂足为点F,且AF的延长线交B′B于点E.证明D′B垂直于平面AEC.求解三棱锥B-AEC的体积,以及二面角B-AE-C的大小.对于第一问的证明,我们可以通过作辅助线AC,运用正四棱锥的性质,利用三垂线定理,来进行证明D′B垂直于平面AEC.对于第二问,我们不难发现直接运用三棱锥体积的求解公式,很难进行解答,因为所需要的线段长度题干中没有给出,也不能快速的进行计算.所以,我们要发散思维,找出与三棱锥B-AEC的体积相同的其他几何图形进行解答,或者我们通过转变三棱锥的顶点来进行计算,通过我们的观察,以点E为顶点,三角形ABC为底面的三棱锥的体积便于解答,底面三角形的面积和三棱锥的高非常容易计算出来.然后通过三棱锥体积的求解公式进行代入求解.对于第三问,求解二面角,首先我们要找到哪一个是所要求解的二面角,只通过表面的观察及二面角的定义,我们可以确定二面角与点F,B有关,再通过分析和作辅助线CF,如图2,最终确定∠BFC为我们所求的二面角,明确自己的求解目标.然后对于这个二面角的计算我们可以通过三角形CBF,运用三角函数进行解答,接下来就是计算我们所需要的线段BF的长度,通过三角形相似的证明求解出线段BF的长度,最后运用三角函数求解出二面角.对于这一道立体几何习题,我们可以从中了解到三棱锥的体积求解的变换,以及二面角的确定,再通过相关立体几何知识的灵活熟练运用.通过我们进行大量的立体几何习题训练,提高做题的效率,在训练中不断进行知识点的总结及相关的转换方法,更加清晰地了解相关题目的解题思想,进一步提高自己的解题能力.
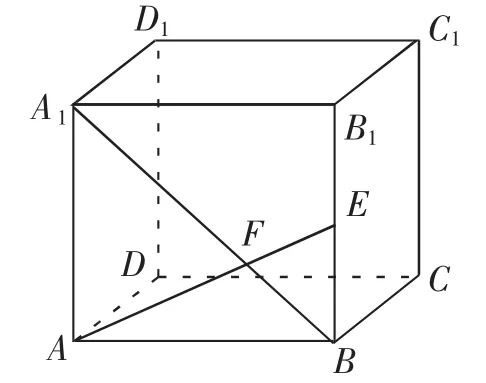
图1
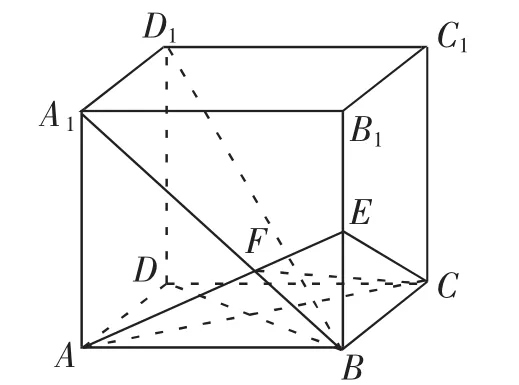
图2
四、合理运用立体几何的解题技巧
在立体几何的解题中,存在一些解题的技巧,我们要熟练地掌握这些技巧,进一步提高立体几何的解题能力,并能够帮助我们进行快速的解答.在解题技巧中,常见的有这几种技巧、割补法、向量法、添加辅助线法等.向量法适合于大部分的立体几何求解中,虽然烦琐但是解题的思路比较简单,而且非常容易进行学习和掌握,只要提高自己的计算能力,就能够正确的解答.所以,向量法是我们在高中立体几何学习中必须要掌握的一种解题方法,而且有的学校只重点进行向量法的讲解.但是,向量法却会在高考中浪费大量的宝贵时间,而且对于一些不适合建立坐标系的立体图形,还需要进行坐标系建立的选择,并不是一个适合的解题方法.辅助线的方法可以说是在立体几何解答中一定会运用的方法,一个辅助线的添加可以让一个难题变得非常简单,由此可见,添加辅助线的重要性.下面我们举例说明辅助线在立体几何解答中的作用.比如下面的这道立体几何习题.如图3,在矩形ABCD中,AB=4,BC=3,E为DC的中点,沿AE将三角形AED折起,使二面角D-AE-B为60度.求DE与平面AC所成角的大小,以及二面角D-EC-B的大小.这道题在一定程度上考验我们的空间思维能力.我们首先要了解当沿着AE折起之后的图形是怎么样的,这样才能进行解答.然后,我们通过对立体图形的观察,找不到DE与平面AC所成角,所以,我们要通过添加辅助线的方法来作出所求的角.作出如图4所示的辅助线,连接OE,得出我们所要求的角为∠DEO,在三角形DOM中利用三角函数的求解公式进行解答.通过所添加的辅助线进行相关线段长度的计算,最后计算出∠DEO.在第二问的解答中,通过自己的思维空间进行画图,作出如图5所示的辅助线进行解答,利用相关的二面角的计算公式进行逐步的解答.针对这道立体几何图形,如果不利用相关的辅助线,不能快速地进行解答.总而言之,辅助线的合理添加能够帮助我们快速地进行解答,在立体几何解题中,合理地运用相关的解题技巧,能够不断提高我们的解题能力.
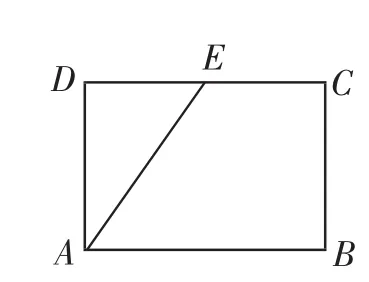
图3
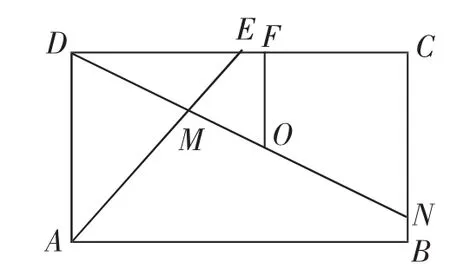
图4
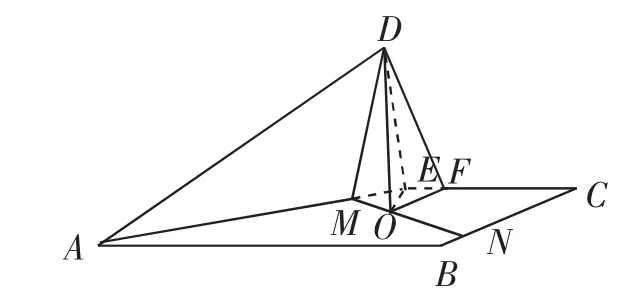
图5
五、优化整理立体几何的错题提高
对于我们高中生来说,数学知识的学习需要花费大量的精力,所以,我们要养成做错题本的习惯来帮助我们进行高效的知识学习.在立体几何知识的学习中,我们会遇到很多的解题技巧和解题思路,其中自然会有我们所没有掌握或者没有见过的,我们要及时地将其通过错题本的方法来记录下来,方便相关知识的记忆和巩固.我们不要以为做错题本会浪费我们的时间,俗话说,好记忆不如烂笔头.如果我们不进行错题本的总结,会逐渐忘记我们知识的漏洞,不能够及时巩固自己的记忆.这样我们之前进行大量的数学习题训练就会变得毫无意义.总而言之,我们要不断整理自己之前做错的题目,然后不断进行巩固和消化,逐渐成为自己的知识,进而提高自己的解题能力.
总而言之,对于高中数学中的立体几何问题,我们要不断进行知识的积累和总结,通过我们大量的立体几何训练,构建出一个完整的立体几何数学知识体系,熟练地运用相关的立体几何集体技巧,最终能够快速准确的进行立体几何的习题解答.对于即将面临高考的我们来说,立体几何的数学知识知识数学学习中的一部分,我们要将这种备考的方法来完美地进行其他知识的学习,在高考的数学考试中取得一个优异的成绩.F
