探索在高中数学合作学习活动中教师的地位和作用*
——以“求椭圆的离心率”为例
2017-06-13筅贵州省铜仁市第二中学覃义超
筅贵州省铜仁市第二中学覃义超
探索在高中数学合作学习活动中教师的地位和作用*
——以“求椭圆的离心率”为例
筅贵州省铜仁市第二中学覃义超
为了省级重点课题“高中数学合作学习经验及其获得能力培养的研究”(2016A028)的研究,在百年名校铜仁市第一中学举行“铜仁市2017年高三复习优质课评选活动”中,笔者上了一节示范课——求椭圆的离心率.课堂教学模式为高考复习课中“合作学习课堂教学模式”的探讨.
一、教师应是合作学习的宽松情境、良好氛围的营造者
面对陌生的学生,首先调节学习的氛围、调动合作学习情境.上课之前,笔者先自我介绍,还特别强调自己的姓读qín不读tán.全班分成六个小组,并讨论确定一个响亮的小组名称:第一小组挑战者;第二小组探索者;第三小组航空母舰;第四小组探月号;第五小组爱国者;第六小组放眼世界.
二、教师应是自主合作学习目标的建设性、创造性的策划者
根据课题内容与教学内容,笔者研制了高中数学“小组合作学习”模式导学案,其模式如下:
学习课题:高考二轮复习圆锥曲线专题系列之(一)——求椭圆的离心率.
学习类型:合作学习:独学(自主学习)→对学(同桌交流)→群学(小组交流)→展示(各小组展示)→总结(汇报收获).
学习内容:用不同的视角求椭圆的离心率.
学习目标:(1)情感、态度与价值观:通过独自学习、同桌交流、小组内深入探讨、激励组间展开充分辩论与展示,让师生享受课堂、共同进步.(2)知识与技能:会求具体题目中椭圆的离心率;从不同的视角探究椭圆的离心率.(3)能力训练目标:由浅入深,由显而隐,以高考真题为载体,实现由已知条件得到什么?求离心率又需要什么?我们要做什么工作?(4)习惯养成目标:自主学习;学会合作;勇于展示;完美表达;大胆质疑;合作共赢!(5)应试重点目标:从题目的已知条件出发,能很快找到解决问题的突破口,很好地完成解答得满分.

图1
例1(2014年江苏高考17题)如图1,在平面直角坐标系xOy中,F1、F2分别是+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
(2)若F1C⊥AB,求椭圆离心率e的值.
第一步:自主学习.
设计意图:通过自主学习让学生对新的学习内容有思考、有疑惑,明白其所要学内容.
第二步:两人互学研讨.
设计意图:两个人探讨,互相讨论学习感受,对于不太理解的问题通讨论进一步掌握.
第三步:小组合作探究.
设计意图:通过小组探讨得到最佳方法,便于代表小组展示.
第四步:组际展示.
展示的内容与形式(请把本小组要展示的方法记下来);展示人员安排(记下代表本小组展示成员的姓名及其方法的优点);展示要求:声音宏亮、条理分明、书写规范.
第五步:反思提升.
自己分享给大家什么方法?自己收获了什么方法?自己的优势与存在的不足、不足之处的弥补措施.
第六步:课外作业.
(1)求C的方程.
(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.
2.(2014年新课标全国卷Ⅱ理科20题)设F1、F2分别是椭圆=1(a>b>0)的左、右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
三、教师应是自主合作学习各小组成员的平等的亲密战友
当学生在对导学案上的试题思考的时候,笔者在各小组之间观察,时而画龙点睛地提醒一句两句,启发学生的思维能力;时而坐在学生身边一起分析研究,探讨最佳方案.讨论十分激烈,思路多种多样.
1.挑战者组的蒲仁荣同学汇报了第一小组的解法
思路1:顺藤摸瓜(整理后的过程).
由已知条件可写出BF2的直线方程与椭圆方程联立求解.因为B(0,b),F2(c,0),所以直线BF2的方程为b,代入椭圆方程
因为F1C⊥AB,所以,所以b4= 3b2c2+4c4,即(b2+c2)(b2-4c2)=0,得b=2c.由a2=b2+c2,得
2.探索者组的刘容泥同学介绍了自己的解题思路(整理后)
点评:以上同学们充分利用了垂直这个条件.亲密伙伴式,把课堂教学看作是师生平等研讨问题,提出和验证假设,参与和体验实验操作,在观察、比较、归纳、分析、综合的思辨过程中生成问题解决方案或结论.
四、教师应是自主合作学习温馨、友善的督导者
在自主合作学习过程中,教师往往采取的是一种督导性的提示,不越位代替学生孕育和产出“结论”,学生难产“结论”时老师又要及时充当热心的结论“助产婆”.
笔者在第三小组航空母舰组的国年军同学身边观察时,发现他的笔尖就在A和C两点转来转去,笔者说,你能不能借用A和C两点的横坐标相等解决.几分钟后,他有了以下做法:联立方程求A和C点的横坐标,两个横坐标相等求离心率.
因为F1C⊥AB且直线AB的斜率,故直线的方程为
五、教师应是自主合作学习的积极态度的调控者
这时,笔者总结说,以上的思路都要解二元二次方程组,能否避开它?第四小组探月号的李光辉同学有漂亮的解法:
思路二:避难就易.
联立直线与椭圆方程,可直接求出A点坐标,然而运算较麻烦.我们避难就易,设A点坐标为(x0,y0),则C点坐标为(x0,-y0),继续寻找与A相关的,点A在直线BF2上,所以(x0,y0)满足bx0+cy0-bc=0,那么由点C在直线F1C上及F1C⊥AB,可得cx0-b(-y0)+x2=0,即cx0+by0+c2=0.当然,点A还在椭圆上,有
点A的坐标满足的关系还挺多!然而,要求离心率,并不需要x0,y0,只需要a,b,c的等式关系即可,因此代入椭圆方程,得
又b2=a2-c2,a2=5c2,所以
自主合作学习是依据教学中教师是主导、学生是主体的这一辩证原理,要求教师尽可能把课堂时间还给课堂的主体和主人——学生.
思路三:回归起点.
第五小组爱国者的吴捷同学有了以下思路(用相似三角形的性质):
如图2,设F1C与AB交于P点,则∠F1PF2=90°,出现了一个直角,而以椭圆的两个焦点为顶点的三角形当首推“焦点三角形”.因此,我们连接F2C,则有CF1+CF2=2a.若F1C,F2C可以a,b,c用来表示,那也就得到了关于a,b,c的等式.我们把目光聚焦在Rt△F1PF2上.能否通过这个直角三角形表示出F1C,CF2呢?
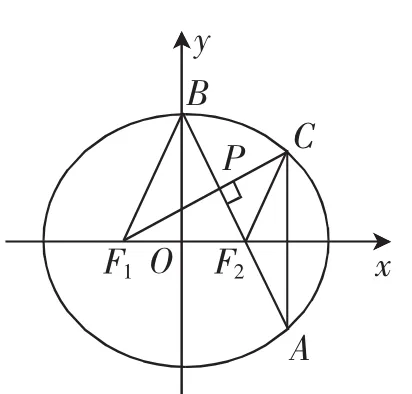
图2
因为Rt△F1PF2的内角∠F1F2P=∠OF2P,所以PF2=然而,我们只要知道是确定的,又CF2与AF2关于x轴对称,所以F2C∥F1B,则△PF2C∽
所以CF1+CF2=由b2=a2-c2消去b,把等式平方得(a2-c2)c2=(a2-3c2)2,同时要注意等价,还应有a2-3c2>0.

这样,从椭圆的定义出发,将已知转化到“焦点三角形”上,获得了等式,在消去b的过程中,若不注意到bc= a2-3c2>0这个特征,就会产生两个解.代数变形时留意等价性,会省去检验的烦恼.
第六小组放眼世界组的池辉同学有如下思路(用三角形函数的知识):
如图3,设∠CF1F2=θ,则
所以∠BF2C=2θ,则∠F1CF2=-2θ,且sinθ=sin∠OBF=,2cosθ=.

图3
在△CF1F2中,由正弦定理知
因为|CF1|+|CF2|=2a,所以,所以,因为b=2c,所以
六、教师应是自主合作学习的积极向上、激励性的评价者
在自主合作学习中,教师是否善于对小组团队进行科学合理评价,不但是一个理论问题,而且是一个亟待完善的实践问题,这也检验着教师在自主合作学习模式中是否完成了真正意义上的转型.笔者在充分肯定以上同学的聪明才智的时候.第一小组的李万奎同学又有了新思路:用椭圆离心率的定义.
由此可见,一个垂直条件实现了“特征三角形BOF2”与“焦点三角形F1CF2”之间很好的沟通.“边→角→边”的两度转化自然而然,一气呵成,顺理成章!
反思:在小组合作学习过程中,教师首先应是自主合作学习宽松情境、良好氛围的营造者.第二,教师应是自主合作学习各小组成员的平等的亲密战友.第三,教师应是自主合作学习的温馨、友善的督导者.第四,教师应是自主合作学习的积极态度的调控者.第五,教师应是自主合作学习的积极向上激励性的评价者.
附课外作业解答:
(2)设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2, y2),M(xM,yM).+=1+1+4kbx+2b-8=
将y=kx+b代入,得(2k2)x220.
所以直线OM的斜率与直线l的斜率的乘积为定值.
(2)由三角形中位线知识可知MF2=2×2,即=4.
设F1N=m,由题可知MF1=4m.由两直角三角形相似,可得M,N两点横坐标分别为c,-c.由焦半径公式可得MF1=a+ec,NF1=a+e△-c2,且MF1∶NF1=4∶1,e=,a2=b2+ c2.联立解得a=7
*本文系省级重点课题“高中数学合作学习经验及其获得能力培养的研究”(课题编号:2016A028)的阶段性成果.
