高考中的递推数列分类例说
2017-06-13筅江苏省张家港市乐余高级中学张森焱
筅江苏省张家港市乐余高级中学张森焱
高考中的递推数列分类例说
筅江苏省张家港市乐余高级中学张森焱
数列是高中数学的一项重点内容,关于递推数列的考查是其中的一个难点,它类型多,解法灵活,技巧性强,是考查学生逻辑推理与转化化归能力的良好载体,也是近年来高考常考的内容.下面介绍对递推数列的几种考查方式,以期抛砖引玉.
一、考查递推数列通项公式的求解
递推关系是给出一个数列的重要形式,求数列的通项公式,是得出一个数列的基本途径,也是转化与化归重要数学思想的应用——化抽象为具体.
方法1:运用累加法求解
这种方法适用于:在数列{an}中,首项a1已知,且满足an+1=an+f(n),数列{f(n)}是可以求和的.
例1已知数列{an}满足a1=1,an+1=an+1 n(n+1),求数列{an}的通项公式.
所以结合已知得

以上n个等式相加得

方法2:运用累乘法求解
它适用于:在数列{an}中,首项a1已知,且满足an+1=
an·f(n),数列{f(n)}是可以求出乘积的,通常·f(1)·a1,常见f(n)有以下2种类型:
(ii)f(n)=kan,(ak≠0,a≠1),即数列{f(n)}为等比数列,其中a为公比,首项为ka.
例2在数列{an}中,已知数列{an}的通项公式.

方法3:构造等差数列法求解
将所求的数列递推关系式变形,构造等差数列.
例3在各项不为零的数列{an}中,已知a1=1,an-1=,求数列{an}的通项公式.
常见构造的等差数列的形式有三种:
一是形如an+1=p·an+qn(p,q为非零常数,且p≠1,q≠1,p=q),此类数列解决的思路是,在an+1=p·an+qn的两边同除以qn+1,即是以为首项,为公差的等差数列;
三是形如an=p·Sn·Sn-1(n≥2)(p为非零常数),解题思路是先利用an=Sn-Sn-1(n≥2)代换an,得Sn-Sn-1=p·Sn·Sn-1,然后两边同时除以Sn-1·Sn,得,-p为公差的等差数列.
方法4:构造等比数列法求解
例4在数列{an}中,已知a1=1,有an+1=3an+2n+1,求数列{an}的通项公式.
n以为首项,为公比的等比数列,即
形如an+1=qan+d(d(q-1)≠0)的递推关系,都可运用构造等比数列的方法,来求其通项公式.具体做法是:设an+1+x=q(an+x),由an+1=qan+d解得是公比为q的等比数列,从而求其通项公式.
方法5:先猜后证
这种数列的通项公式问题,需要先求出这个数列的前若干项,寻找其规律,猜想其结果,然后用数学归纳法证明其正确性.
例5在数列中{an}中,已知对任何正整数n恒成立,求数列的前4项,猜测其通项公式,然后用数学归纳法证明其正确性.
解:当n=1时,a1=1.
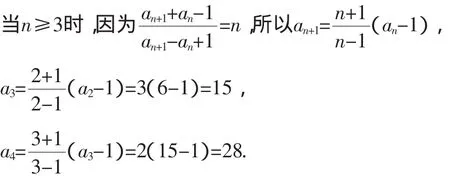
应有an=n(2n-1)=2n2-n,下面应用数学归纳法证明其正确性.
①当n=1,2,3,4时,结论当然成立;
②假设当n=k时结论成立,即ak=2k2-k,
所以当n=k+1时结论也成立.
综合①与②得,对任何正整数n,an=2n2-n恒成立.
递推数列的类型多种多样,求解递推数列通项公式的方法也有很多;可是,只要我们辨清它是哪种类型,用对应方法解决它即可;万变不离其宗,很明显它们的实质是通过合理、适当的转化、化归,转变为求解等差数列或等比数列的有关问题而已.
二、考查不等递推关系
不等递推关系型时常出现在一般的竞赛或模考中,此类问题呈现简洁,看似平淡无奇,却极富韵味.
例6已知f(x)是定义在R上的函数,对任意实数x,都有f(x+3)≤f(x)+3和f(x+2)≥f(x)+2,若f(1)=1.
(1)求f(2005)的值;
(2)求f(2007)的值.
解:(1)联想等差数列的通项公式的推导,试用叠加法.
由f(x+3)≤f(x)+3这个“不等递推关系式”,得f(2005)≤f(2002)+3,f(2002)≤f(1999)+3,f(1999)≤f(1996)+ 3,…,f(4)≤f(1)+3,将这668个不等式两边相加得f(2005)≤f(1)+3×668=2005.
由f(x+2)≥f(x)+2这个“不等递推关系式”,得f(2005)≥f(2003)+2,f(2003)≥f(2001)+2,f(2001)≥f(1999)+2,…,f(3)≥f(1)+2,将这1002个不等式两边相加,得f(2005)≥f(1)+2×1002=2005.
据“两边夹法则”,得f(2005)=2005.
(2)【思路一】仿(1)直接叠加不便求解,可尝试将已知递推式变形后再使用叠加法.
由f(x+2)≥f(x)+2,得f(x+1)+2≤f(x+3),又f(x+3)≤f(x)+3,所以f(x+1)+2≤f(x)+3,即f(x+1)≤f(x)+1.
由f(x+1)≤f(x)+1,得f(2007)≤f(2006)+1,f(2006)≤f(2005)+1,f(2005)≤f(2004)+1,…,f(2)≤f(1)+1,将这2006个不等式两边相加,得f(2007)≤f(1)+2006=2007.
由f(x+2)≥f(x)+2,得f(2007)≥f(2005)+2,f(2005)≥f(2003)+2,f(2003)≥f(2001)+2,…,f(3)≥f(1)+2,将这1003个不等式两边相加,得f(2007)≥f(1)+2×1003= 2007.据“两边夹法则”,得f(2007)=2007.
【思路二】思路一操作起来比较麻烦,若能把“不等递推关系式”转化为“相等递推关系式”,则问题就变得熟悉了.
同思路一中步骤,得f(x+1)≤f(x)+1,①
由f(x+2)≥f(x)+2,得f(x+1)≥f(x-1)+2.又由f(x+3)≤f(x)+3,得f(x-1)≥f(x+2)-3.所以f(x+1)≥f(x-1)+2≥f(x+2)-3+2=f(x+2)-1≥f(x)+2-1=f(x)+1,即f(x+1)≥f(x)+1.②
综合①②知,f(x+1)=f(x)+1.所以通项为f(n)(n∈N*)的数列是等差数列,其首项f(1)=1,公差d=1,
所以f(2007)=1+(2007-1)×1=2007.
【思路三】思路二应用“两边夹法则”,变“不等递推关系式”为“相等递推关系式”,然后用等差数列的知识使问题求解得到简化.若对解法的探究就此止步,是否意犹未尽?联想数列求某一项的值常用周期数列法,故一鼓作气作如下探索.
f(x+3)≤f(x)+3圳f(x+3)-(x+3)≤f(x)-x,且f(x+2)≥f(x)+2圳f(x+2)-(x+2)≥f(x)-x,为此构造函数g(x)= f(x)-x,则g(1)=f(1)-1=0,且g(x+3)≤g(x),g(x+2)≥g(x).
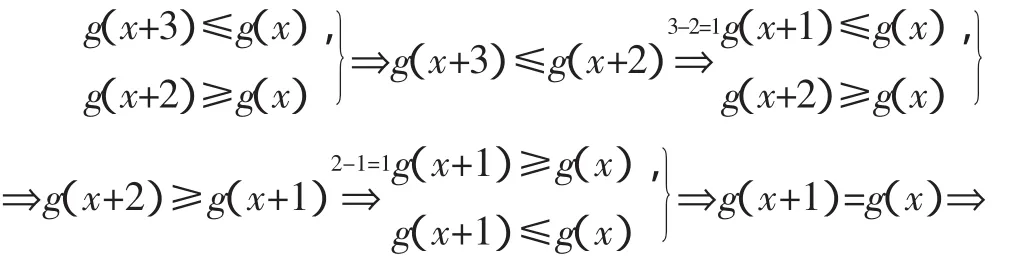
通项为g(n)(n∈N*)的数列是周期数列,且其周期T=1圯g(2007)=g(1)=0圯f(2007)=g(2007)+2007=2007.
三、考查递推数列的值域
对于数列{an},若设集合M={an|n∈N*},则M是数列{an}的值域.数列的值域有可能成为高考的新亮点.
例7已知无穷数列{an}满足an+1=-2a(nn∈N*),若集合M={an|n∈N*}中只有二个元素,求数列{an}首项a1的值.
解:显然a1≠a2(若a1=a2,则a3=f(a2)=f(a1)=a1,其中f(x)=x2-2x,依此类推数列{an}为常数列,与已知矛盾),从而a3=a2与a3=a1中有且只有一个成立.
(1)当a3=a2时-2a2=a2,则a2=0,或a2=3.若a2=0,则a1=0(舍去,此时an=0),或a1=2;若a2=3,则a1=3(舍去,此时an=3),或a1=-1.
(2)当a3=a1时,(-2a)12-2(-2a)1=a1,即a(1a1-3)(-a1-1)=0,则a1=0(舍去,此时an=0),或a1=3(舍去,此时an= 3),或
综上a1的取值有
事实上,本例只不过是函数的不动点与二阶周期点在数列值域问题中的一个应用.先熟悉两个概念——函数的不动点与二阶周期点:已知函数y=f(x),x∈I,若存在x0∈I,使得f(x0)=x0,则称为函数y=f(x)的不动点;已知函数y=f(x),x∈I,若存在x0∈I,使得f(f(x0))=x0且f(x0)≠x0,则称为函数y=f(x)的二阶周期点.当a1=2时,{an}为:2,0,0,…;当a1=-1时,{an}为:-1,3,3,…这两种情况说明a2是函数f(x)=x2-2x的不动点.当时,{an}为:a1,a2,a1,a2,…,这时a1,a2是函数f(x)=x2-2x的二阶周期点.同样依此类推若{an}的值域M为三元集,问题本质是函数的不动点与三阶周期点.
