高中数学核心素养背景下课堂教学研究
——以一元二次不等式及其解法教学设计为例
2017-06-13筅江苏省如东高级中学惠敏敏
筅江苏省如东高级中学惠敏敏
高中数学核心素养背景下课堂教学研究
——以一元二次不等式及其解法教学设计为例
筅江苏省如东高级中学惠敏敏
随着课程改革的实施,教育部在2015年在《教育部关于全面深化课程改革落实立德树人根本任务的意见》中提出了“核心素养”的理念,并将这一理念深化到了新一轮的课程过改革当中.该核心素养体系主要包含了社会责任、国家认同、国际理解、人文底蕴、科学精神、审美情趣、身体健康、学会学习、实践创新等九个方面.那么我们如何在核心素养理念的引导下,改善我们的高中数学教学呢?将核心素养的理念转变到教学当中主要体现在学生的自主发展、合作参与和创新实践方面,因此在数学教学的过程中要突破传统意义的教学模式,不能够仅仅是将传授知识作为课堂教学的根本,还要注重学科价值的体现和拓展,注重学生数学思维的培养,体现出学生在课堂教学中的主体地位,进而培养学生数学学习的志趣.[1]
一、一元二次不等式教学内容概述
一元二次不等式是继初中阶段学习的一元二次方程和一元一次不等式的又一提高,是高中数学函数、数列等部分学习的基础,并且,在高考数学中,很多题目都涉及到了一元二次不等式的相关知识.因此,一元二次不等式是高中数学课程的重要组成部分.为了响应新课程改革中“核心素养”理念的号召,在该部分教学设计中,教师可以结合多种数学思想来辅助教学设计,例如,可以利用分类讨论思想、转化与化归思想、数形结合思想等来帮助学生建立良好的数学思维方式,培养他们的创新精神.
二、一元二次不等式教学设计
1.教学目标
首先,通过本节课的教学能够让学生理解一元二次不等式与之相对应的方程和函数的联系.其次,通过生活场景的创设,能够提高学生利用所学知识解决现实生活中实际问题的能力,并且通过解题的讲解,渗透数形结合的思想,培养学生的数学思维,养成科学的精神.
2.教学过程设计
(1)问题引入阶段
为了能够引起学生的学习兴趣和加强新旧知识之间的联系,教师选择了最贴近学生生活的关于等差数列的练习题,这样不仅复习了前边与一元二次不等式相关的知识,还培养了学生将现实生活问题转化为数学问题的能力,从而培养学生有计划地进行数学学习的习惯,使学生学会学习.为了让学生真实地感受不等式的意义,教师可以在第一题的基础上作进一步的延伸,让学生体会数学的现实价值.
例1某超市正在做文具促销活动,其中A类钢笔的价格是1.5元一支,而B类钢笔的价格随着购买数量的不同而不同,具体的价格如下所示.为了能够让更多的顾客参与活动,超市对这些钢笔实施限购,每人最多购买17支.

B类钢笔价格变动表
问题1:通过B类钢笔的价格表,你发现了什么规律?
问题2:小红需要买多少钢笔才能够保证A类钢笔的价格不大于B类钢笔的价格?
问题解析:通过对B类钢笔的价格分析可以看出,B类钢笔的价格随着购买数量的增加逐渐减少,构成了d=-0.1的等差数列,则bn=1.7+(n-1)(-0.1)=1.8-0.1n.在第二问中,假设小红买x支钢笔,那么就可以根据题目中“A类钢笔的价格不大于B类钢笔的价格”的条件列出不等式,从而求出x的值.
(2)明确概念,自主探究不等式的解法
根据在问题引入部分问题的解答列出一元二次不等式,并引导学生总结一元二次不等式的概念:在不等式中,含有一个未知数,并且未知数的最高次数是2.为了锻炼学生的思维,使学生形成自己的不等式解题思路,教师可以通过让学生自主探究一元二次不等式解法的方式来进行不等式解法的教学.通过学生的自主探究,教师能够更好地发现学生对该部分知识的理解程度,便于教师开展教学,还有助于提高学生学习该部分知识的积极性.[2]
(3)教师引导,探究解题方法
教师首先引导学生正确认识一元二次不等式、一元二次方程和二次函数之间的关系,通过二次函数和一元二次方程的解法,来引出不等式的解法:一元二次方程的实根就是二次函数的零点.通过对二次函数进行作图,就可以直观地看出相对应不等式的解集,这就是方程与函数思想和转化与化归思想的具体应用,另外,借助函数图像能够将抽象的数学问题转化为直观具体的数学问题,是数形结合思想在解不等式部分的具体应用.
(4)通过图像,总结解法
在该部分教学中,教师利用问题引入部分的二次函数不等式,让学生做出二次函数y=x2-5x的图像,并让学生仔细观察图像,讨论图像信息.相融合,通过具体的实例,帮助学生建立数学分析与讨论的思维方式,使得学生在理解上更加容易.
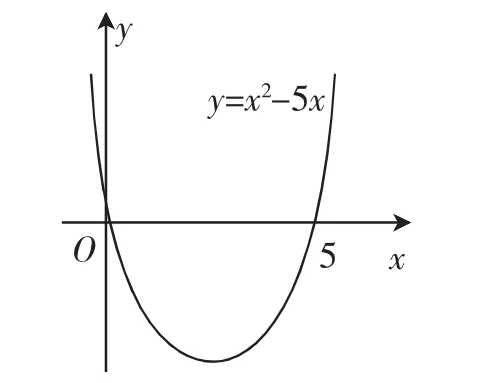
图1
(5)优化思维,规范解题
在该部分的教学设计中,教师通过具体的例题,以规范的板书帮助学生规范解题的步骤,使学生由感性认识向理性认识过度,并在这个过程中将相关的数学思想作进一步的整理.
例2求出不等式-x2+3x+4>0的解集.
首先,将这一不等式进行标准化转化,变为:x2-3x-4<0;之后根据判断方程x2-3x-4=0的根;最后,通过画二次函数y=-x2+3x-4=0的图像,进而求出不等式的解集{x|-1 (6)强化练习,及时反馈 进行完该部分的教学后,为了检测学生对于该部分知识的掌握和帮助他们熟练解题的技巧,可以通过练习竞赛的方式来实现. 例3求解下列不等式的解集: (1)x2-4x+7>0; (2)-x2-x+5>0; (3)-3x2+2x+6>0. 通过练习,将学生书写不规范和做题不正确的典型部分拿出来让学生共同评价和改正,从而使学生加深印象. (7)课堂小结 在该部分,教师组织学生对所学知识进行自主总结,通过学生的自我总结掌握学生的学习状况,之后再有教师做最终总结,并强调学习的重点和易犯错误,培养学会善于反思和总结的习惯. 通过观察图像学生可以总结出:当x<0或x>5时,图像就在y轴的上方,即y的取值就是正数;当x=0或x=5时,图像正好在x轴上,那么y=0;当0 在该部分的教学中,教师利用几何画板引入二次函数图像,将数学思想中的数形结合思想和现代教学手段 核心素养的提出为高中数学课程改革指明了方向,在本节课的教学设计中,教师坚持学生的主体地位,引导学生自主探究并渗透相应等数学思想,不仅使学生掌握了相关的知识和技能,还锻炼了学生的思维,提高了他们的创新能力,体现了核心素养的要求. 1.中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:人民教育出版社,2012.3.1. 2.李正兴主编.高中数学思想方法[M].上海:上海科学普及出版社,2015.7.1.三、总结
