含间隙运动控制系统中的定位抖动和速率波动原因分析及解决措施

麻恒进，程亚静，孟凡军，罗秀芳

（北京航空精密机械研究所，北京100076）

含间隙运动控制系统中的定位抖动和速率波动原因分析及解决措施

麻恒进，程亚静，孟凡军，罗秀芳

（北京航空精密机械研究所，北京100076）

针对一类含间隙大惯量非直驱转动系统中出现的速率波动现象，利用描述函数法和计算仿真的方法进行了原因分析。在通常的解决措施如双电机消隙、机械消隙方法之外，针对一类间隙可测量的运动控制系统，提出了解决该类问题的新思路，即通过间隙的间接测量，利用反馈机制进行间隙补偿，并用小增益定理证明了其稳定性。实现了部分电气消隙的作用，在适当降低跟踪精度的情况下，消除了定位抖动，提高了速率平稳性。

运动控制；间隙；定位抖动；速率波动；间隙反馈补偿

0 引言

运动控制系统有很多应用场合，如数控机床、大型天线以及为被测件提供特定姿态的测试设备等。从定性的方面来说，一般要求定位快速准确、运动平稳、安全可靠。按传动形式一般分为直接驱动系统和非直接驱动系统，直接驱动系统在驱动电机和被驱动部件之间无其他传动环节，一般用于负载较小，动态性能和定位精度要求较高的场合，驱动电机一般选择直流或交流力矩电机；非直接驱动系统则一般选择伺服电机，再通过传动环节，如减速器、蜗轮蜗杆、齿轮齿条等驱动机构运动，一般用于负载较大，动态性能要求不高，主要实现定位和匀速运动的场合。

对于非直驱运动控制系统，由于传动环节的特性，一般均存在间隙这种非线性因素。间隙的存在，使得系统总体运动特性恶化，主要表现为定位抖动和速率波动，对于转动惯量变化非常大的系统，受到的影响就会更加明显［1］。当然，系统中还存在着其他非线性因素，如死区、摩擦力。一般认为死区为位置固定的间隙或反过来，间隙是位置可移动的死区。对于摩擦力，其形成机理较复杂，但往往表现出一定的滞环特性［2］，从而也具有部分间隙的性质。

本文针对一类含间隙大惯量非直驱转动系统中出现的定位抖动和速率波动现象，利用描述函数法和计算仿真的方法进行了原因分析。在通常的解决措施如双电机消隙、机械消隙［3-4］方法之外，针对一类间隙可测量的运动控制系统，提出了解决该类问题的一种新思路。即通过间隙的间接测量，利用反馈机制进行间隙补偿，从而实现了部分电气消隙的作用，消除了定位抖动，提高了速率平稳性。

1 系统模型及原因分析

1.1 系统模型

对于非直驱转动系统，一般组成包括：伺服电机、传动机构、测量反馈部件、控制器、伺服驱动器以及辅助模块等，简化的系统结构示意图如图1所示。

测量反馈部件包括两部分，一部分为伺服电机转动轴尾端的测量单元，一般有旋转变压器和编码器两种形式，主要作用是测量电机转子位置，控制伺服驱动器内的电流矢量，附加的作用是可由此信号获得电机转子的位置和速度信号，从而在驱动器内完成伺服电机的位置环和速率环控制。另一部分测量反馈单元则安装于负载末端，为转动定位控制的主测量单元，转台能达到的最高定位精度一般受该传感器的精度限制。本文针对的系统配置是由伺服电机、电机端测量单元、伺服驱动器实现速率环控制，而位置环则由主测量单元和多轴运动控制器完成。

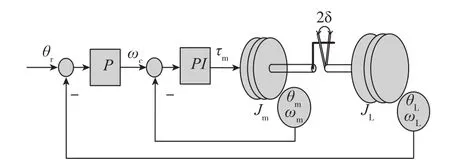
图1 系统结构示意图Fig.1 Schematic of the system structure

其中，θr为设定角度值，rad；P为位置环比例控制器；ωc为速度指令，rad/s；PI为速率环比例积分控制器；τm为电机力矩指令，Nm；θm为电机端测量单元的输出角度值，rad；ωm为电机端测量单元输出的速度解算值，rad/s；Jm为电机转子转动惯量，kg·m2；θL为负载侧测量单元的输出角度值，rad；ωL为负载侧测量单元输出的速度解算值，rad/s；JL为负载转动惯量，kg·m2；δ为间隙值，rad。

在系统实际使用过程中，当负载惯量增加较大时，系统进行速率运动时会出现速率波动现象，具体表现形式为速率时大时小，目测可观察到时走时停的宏观现象。针对这一现象，对系统进行了详细分析，含间隙的运动控制系统传递函数如图2所示。图2对该系统分别进行了描述函数分析和计算机仿真分析，解释了出现速率波动现象的原因。

图2 含间隙特性的系统传递函数Fig.2 Transfer function of the system with backlash

1.2 描述函数法速率波动原因分析及计算机仿真结果

描述函数法是分析非线性控制系统稳定性的一种方法，其基本思想是：将系统分为线性环节和非线性环节两个部分，对非线性环节采用正弦输入时等效增益的方法，即将非线性环节等效为一个幅值和相位随输入信号变化的复增益环节，从而可与线性环节部分共同采用频率域的分析方法进行系统稳定性分析。

如图3所示，一般间隙的模型为：

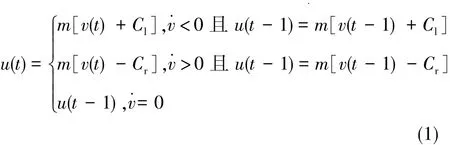
其中，m为与减速比有关的斜率，u（t）为间隙的输出，v（t）为间隙的输入；Cl为左间隙；Cr为右间隙。一般情况下，左间隙与右间隙相等。

不失一般性，本文选择m＝K＝1，Cr＝Cl＝b＝0．1。

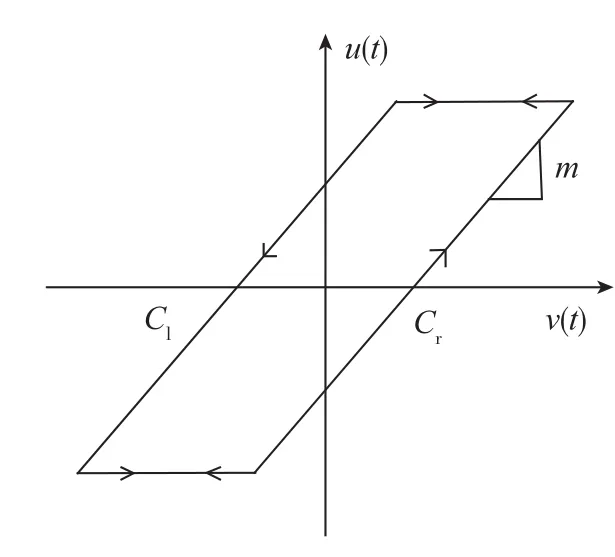
图3 间隙模型Fig.3 Model of the backlash

其描述函数为：

其中，A为输入正弦信号的幅值。

（1）小惯量时的稳定性分析及计算仿真

设此时J＝4，将间隙的负倒描述函数-1/N（A）和线性部分G（s）的幅相曲线绘于复平面内，如图4所示。可以看出，间隙的负倒描述函数与线性部分的幅相曲线没有交点。因此，系统是稳定的，没有自持振荡，也就没有定位抖动和速率波动现象。此时，系统的阶跃响应计算仿真结果为：系统有静差，但系统稳定，无定位抖动现象，如图5所示。

图4 小惯量时的负倒描述函数和线性部分的幅相曲线（J＝4）Fig.4 Negative inverse describing function and the magnitude-phase curve of the linear part when the moment of inertia is small（J＝4）

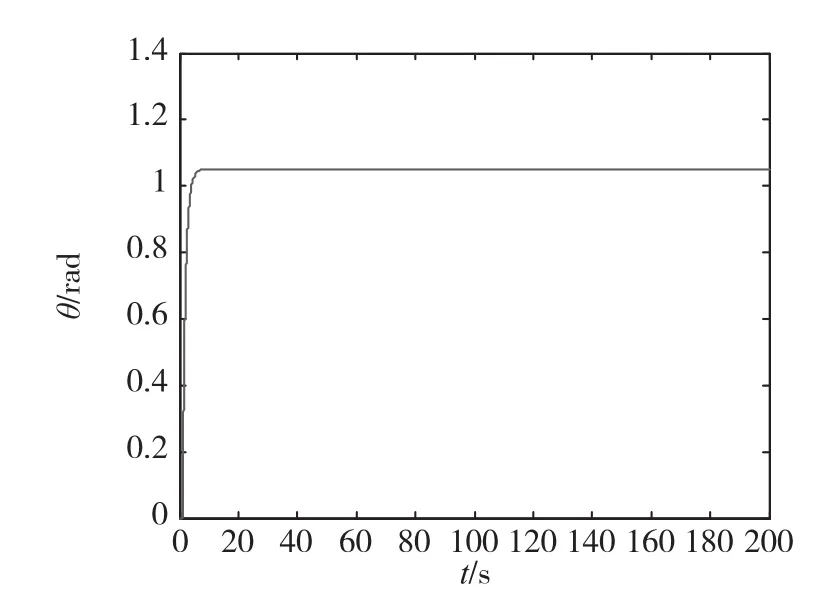
图5 小惯量时阶跃响应计算仿真（J＝4）Fig.5 Digital simulation of the step response when the moment of inertia is small（J＝4）

（2）大惯量时的稳定性分析及计算仿真

设此时J＝400，间隙的负倒描述函数与线性部分的幅相曲线如图6所示，二者相交且在交点处形成自持振荡，对应频率为0．189Hz；此时，系统的阶跃响应计算仿真结果如图7所示，可观察到明显的速率波动现象，且振荡周期与描述函数法分析的结果一致，均为5．2s左右。

由此可以看出，大惯量时定位抖动和速率波动产生是间隙和线性部分特性的改变引起的。

图6 大惯量时的负倒描述函数和线性部分的幅相曲线（J＝400）Fig.6 Negative inverse describing function and the magnitude-phase curve of the linear part when the moment of inertia is big（J＝400）

2 解决措施

从上文的分析可知，解决定位抖动和速率波动的措施，可从两个方面展开。一是调整线性部分的特性，使之不与间隙的负倒描述函数相交，一般的调整方法是，增大速率环比例增益，同时减小积分增益（或提高积分时间）。该种方法若调整合适，可以消除自持振荡。但对于大惯量系统，由于惯量的增加，往往伴随着负载尺寸的增加以及刚度的降低，负载的最低扭转频率变得很低，从而限制了参数调整的范围，一般难以达到与小惯量负载时同样的系统特性。另一个途径是调整间隙的大小，但由于间隙的固有特性，一般只能调整振荡幅值的大小，而不能消除自持振荡，且机械调整间隙的方法成本较高。

针对间隙消除的方法，传统的措施包括机械消隙法和双电机消隙法。机械消隙法如双齿轮或双蜗轮法等，经过仔细调整，可以将间隙调整到一定范围内。而双电机消隙法则从电气控制上，通过一定的控制策略，在牺牲部分效率的基础上可以达到相对理想的效果，由于采用两套驱动系统，相对成本较高。

另一种直观的想法是采用间隙模型的逆模型［5-6］，用算法实现逆模型从而达到补偿间隙的作用。其基本思想是：使间隙前面的部分，在需要经过间隙时，以尽可能短的时间运动过间隙。理论上的特性带有阶跃形式信号，如图8所示。该种模型理论上是可行的，但物理上是难以实现的，因此又有学者提出了一些光滑函数的方法［7］，但物理意义并不明确。

本文针对间隙可测量的一类大惯量转动系统，提出了一种间隙反馈控制方法，利用间隙前后的输出差别，反馈输出至速率环输入端，从而减小了间隙的影响，提高了速率平稳性。该方法物理意义明确，即通过测量间隙的影响，利用反馈机制，利用执行机构减弱间隙的影响。

控制原理框图如图9所示，其中间隙的测量是通过电机端多圈绝对编码器和负载端绝对编码器之间的差值得到的。

对于如图9所示的控制系统，稳定性证明如下：

不失一般性，设G1（s）稳定，控制原理简化图如图10所示，将虚线右侧的部分视为反馈环节，根据间隙δ的大小，分两种情况分析：

1）δ＝0时，此时没有间隙，求差模块的两个输入完全相等，则输出为0。因此，相当于反馈环节为0，由于G1（s）稳定，因此系统总体是稳定的。

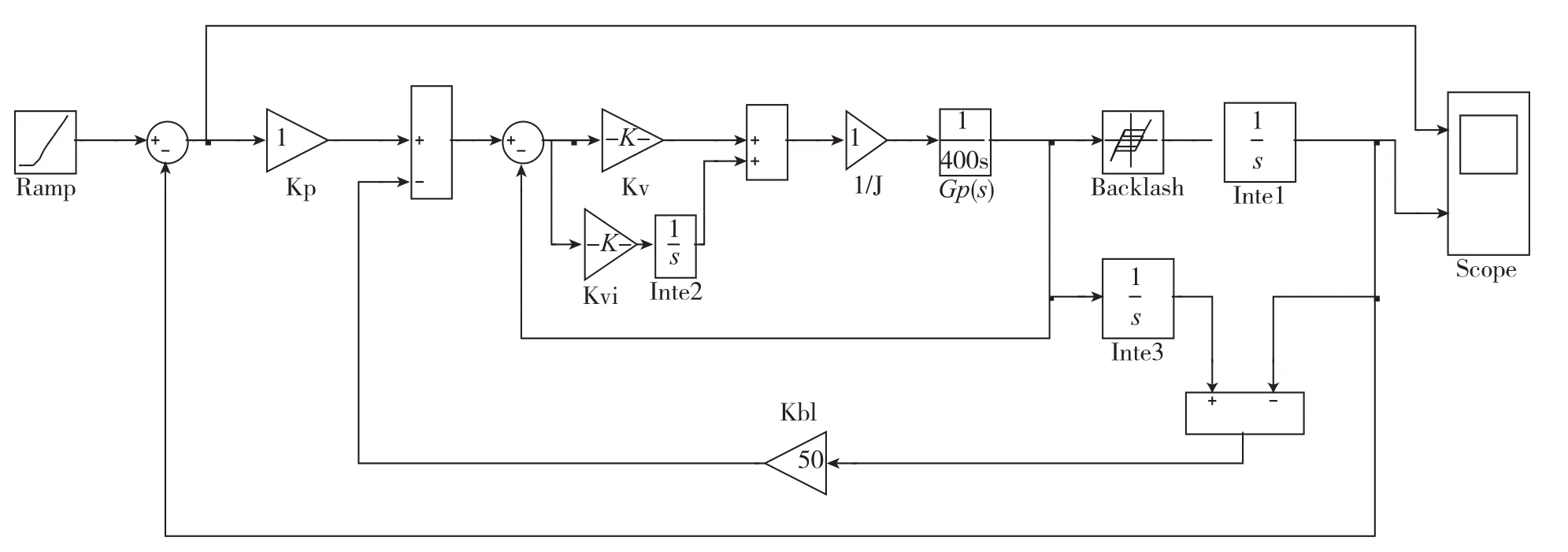
图9 间隙反馈控制系统Fig.9 Backlash feedback control system

因此，该反馈控制系统是条件稳定系统，通过调整Kf可以保证系统的稳定性。

图10 稳定性分析简化图Fig.10 Schematic of the stability analysis

利用计算仿真的方法，增加间隙反馈控制和未增加间隙反馈控制时系统的速率运动跟踪曲线分别如图11、图12所示，可知速率平稳性得到很大提高，已无明显的速率波动。

图11 未加入间隙反馈控制时的跟踪误差曲线Fig.11 Tracking error without backlash feedback control

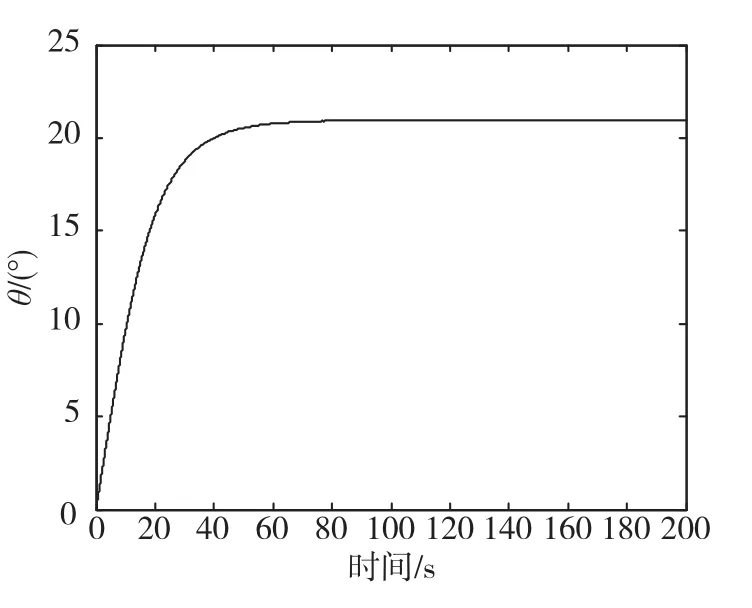
图12 加入间隙反馈控制时的跟踪误差曲线Fig.12 Tracking error with backlash feedback control

由以上仿真结果可以看出，加入间隙反馈控制后，消除了速率爬行现象，但跟踪误差变大了，相当于降低了系统增益，因此，从最终效果上看，该措施是在牺牲一定的跟踪精度情况下获得需要的速率平稳性。

3 试验结果

针对某一大惯量试验转台控制系统，未采取措施前，指令速率为0．15（°）/s，加速度为0．1（°）/s。通过记录的指令和实际速率值，可以看出运动过程中出现了明显速率波动现象，如图13所示。参数调整后，速率跟踪曲线如图14所示。此时，速率跟踪曲线已无明显波动现象，系统特性得到了很大改善。

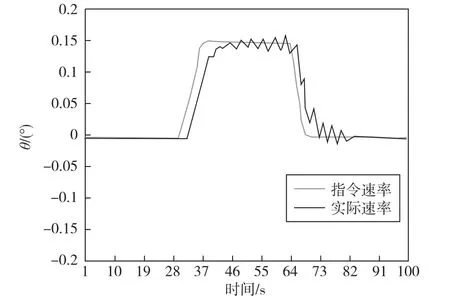
图13 参数调整前速率跟踪曲线Fig.13 Velocity tracking error before parameter adjustment

图14 参数调整后速率跟踪曲线Fig.14 Velocity tracking error after parameter adjustment

4 结论

本文针对一类含间隙大惯量非直驱转动系统中出现的速率波动现象，利用描述函数法和计算仿真的方法进行了原因分析，在通常的解决措施如调整速率环参数、双电机消隙、机械消隙方法之外，针对一类间隙可测量的运动控制系统，提出了解决该类问题的一种新思路，即通过间隙的间接测量，利用反馈机制进行间隙补偿，从而实现了部分电气消隙的作用，在适当降低跟踪精度的情况下，消除了定位抖动，提高了速率平稳性。

［1］张新华，杨瑞峰．含间隙的电动伺服机构非线性振荡［J］．振动、测试与诊断，2013，33（S2）：131-136+224．ZHANG Xin-hua，YANG Rui-feng．Nonlinear oscillations in electromechanical actuation system with clearence［J］．Journal of Vibration，Measurement＆Diagnosis，2013，33（S2）：131-136+224．

［2］Åström K J，Canudas-de-Wit C．Revisiting the lugre friction mode［J］．IEEE Control Systems Magazine，2008，28（6）：101-114．

［3］张童，李英杰，蒋君平．几种消隙驱动结构在机床回转工作台上的应用［J］．组合机床与自动化加工技术，2012（8）：110-112．ZHANG Tong，LI Ying-jie，JIANG Jun-ping．The application of eliminating backlash driver structure in rotary tables of themachinetool［J］．ModularMachineTool＆Automatic Manufacturing Technique，2012（8）：110-112．

［4］刘攀玲，张光辉，刘妙，等．基于偏置力矩的双电机消隙智能PID控制［J］．火炮发射与控制学报，2015，36（2）：50-53．LIU Pan-ling，ZHANG Guang-hui，LIU Miao，et al．Intelligent PID control of double motor anti-backlash based on bias torque［J］．Journal of Gun Launch＆Control，2015，36（2）：50-53．

［5］Tao G，Kokotovic P V．Adaptive control of systems with sensors and actuator nonlinearities［M］．John Wiley and Sons，Inc．，1996．

［6］Zhou J，WenC．Adaptivebacksteppingcontrolof uncertain systems［J］．Lecture Notes in Control＆Information Sciences，2008，372（4）：268-272．

［7］Nordin M，Gutman P O．Controlling mechanical systems with backlash-a survey［J］．Automatica，2002，38（10）：1633-1649．

Analysis and Solvent of Position Jitter and Speed Fluctuation in Motion Control System with Backlash

MA Heng-jin，CHENG Ya-jing，MENG Fan-jun，LUO Xiu-fang
（Beijing Precision Engineering Institute for Aircraft Industry，Beijing 100076）

Analysis of the speed fluctuation in an indirect drive rotating motion system with backlash and big moment of inertia is carried out using the method of describing function and digital simulation，then a new method is provided for a class of motion system in which backlash can be measured，this method is different from the normal methods such as mechanical double gear backlash elimination，double motor backlash elimination et al．The new method is based on feedback mechanism by indirect measuring the value of the backlash and the stability is proved by the small gain theorem．We realized the partly elimination of the backlash，rejecting the position jitter and improving the velocity smoothness under slightly reduced tracking accuracy．

motion control；backlash；position jitter；speed fluctuation；backlash feedback compensation

U666．1

A

1674-5558（2017）05-01318

10．3969/j．issn．1674-5558．2017．03．014

麻恒进，男，硕士，测试计量技术及仪器专业，高级工程师，研究方向为惯性测试与运动仿真技术。

2016-09-02