二维紊流场对飞艇水平面内运动影响研究

王 鹤，李智斌

（1．北京控制工程研究所，北京100190；2．空间智能控制技术重点实验室，北京100190；3．中国科学院光电研究院，北京100094）

二维紊流场对飞艇水平面内运动影响研究

王 鹤1，2，李智斌3

（1．北京控制工程研究所，北京100190；2．空间智能控制技术重点实验室，北京100190；3．中国科学院光电研究院，北京100094）

大气紊流是影响高空飞艇水平面内巡航的重要原因，传统Dryden模型采用谱分解定理，只能生成一维大气紊流模型，对于高空飞艇复杂的飞行运动来说，生成二维紊流风场模型是必要的。基于紊流场的空间相关特性，采用离散自递归方法构建风场模型，然后结合风速矢量三角形关系式，建立扰动下的飞艇动力学模型，再对该模型进行水平竖直解耦。仿真结果表明，大气紊流作用在飞艇上的力会使飞艇较大程度地偏离其运动航迹，呈不稳定的随机波动状态。因此，构建高空飞艇动力学模型时，要充分考虑大气紊流的影响。

大气紊流；二维紊流场；飞艇动力学模型

0 引言

平流层飞艇具有生存能力强、驻空时间长、性价比高、覆盖范围大等优势，可以用于对地观测、勘探目标、运输货物，因此成为各国研究热点。平流层气象条件稳定，风速较低，适合飞艇长期悬停。

尽管平流层气象条件良好，但大量研究表明，高空飞艇所处大气环境比较复杂特殊，尤其风场的随机不确定性干扰对飞艇航迹和定点悬停影响显著，不容忽视。飞艇属于典型的低动态飞行器，低空空速一般为13．9m/s～41．7m/s。由于螺旋桨在高空稀薄大气的工作效率低，所以飞艇在高空能够产生的空速更低。但根据真实气象数据，即使在平流层海拔20km的高度，冬季平均风都会超过40m/s。据报道，谷歌气球在平流层187天内整整环绕地球跑了9圈，可见风场对浮空器位置影响极大。

工程中一般采用传统的Dryden模型对风场进行模拟，即紊流风速可视作随机过程。仿真时先求取紊流风速的传递函数，然后输入白噪声，输出即为紊流风速［1］。但许多工况下，例如飞艇航迹进行动态优化、飞艇编队飞行等，一维紊流场具有较大的局限性，难以满足仿真需求。为了更准确地反映风速对飞艇飞行活动的影响，同时为了后续控制系统设计的需要，需要建立二维紊流风场模型。

另外，已公开发表的大量关于飞艇动力学建模的文献中，仅描述了作用在飞艇上的外力和外力矩与运动状态变量之间的函数关系［2］，没有明确给出风场环境对飞艇的影响，因而不能准确反映复杂环境下飞艇的飞行规律。因此本文在传统六自由度飞行器动力学模型基础上，构建可信度高的风场扰动下的飞艇动力学模型。

1 大气紊流模型

大气紊流是一种较为复杂的物理现象，在实际工程应用中，如本文研究紊流风速对飞艇运动特性的影响时，一般采用合理地假设［3］，建立可靠、简化的工程模型。

1.1 大气紊流基本假设

（1）平稳性和均匀性假设

假设大气紊流的统计特性不随时间和位置发生变化，因此飞行器在大气中飞行时，紊流风速可视作平稳随机过程。

（2）各项同性假设

假设大气紊流的统计量不随坐标系的旋转而变化，与方向无关。因此研究紊流风速时，可以任意假设坐标轴的方向。相关研究表明，该假设适用于中高空紊流。因此对海拔20km的平流层飞艇来说，该假设是可行的。

（3）Gauss分布假设

假设紊流风速大小服从正态分布。

（4）Taylor冻结场假设

一般情况下，紊流风速度Uw是时间t和空间位置r的函数。满足：

当飞艇在大气中运动时，它受到的风速变化率为：

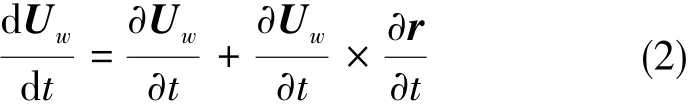
假设紊流速度的改变量相对飞艇速度足够小，可以忽略不计，即当式（2）右边第1项远小于第2项时，式（2）可近似化为：

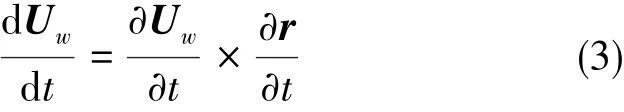
上述过程称为Taylor冻结场假设。

1.2 传统紊流模型的局限性

传统生成紊流风场方法的局限性［4-5］在于：一维紊流风场模型无法推广到高维，因为无法按照假设条件将空间频谱函数转化成时间频谱函数；另外，二维紊流场无法像一维紊流场那样生成滤波器函数，因为难以生成二维紊流场。

文献［6］给出生成二维紊流风场的方法，即分别沿x、y方向生成一维速度序列，如图1所示。

图1 二维紊流网格Fig.1 Turbulence grid of two dimensional

图1表明，（i，j）点的风速值大小为x、y方向序列在该点处的算术平均值，即：

按式（4）可生成整个紊流网格序列，但这样有很大的局限性。从图2可以看出，这会使（i，j）点处的紊流值仅与（i-1，j）有关，而与点（i，j-1）无关。

图2 二维紊流相关点Fig.2 Turbulence related points of two dimensional

实际上，只有当二维紊流场是独立的随机过程时，即满足式（5），该结论才成立。

对于Dryden模型，纵、横向相关函数分别如下：

由式（7）得：

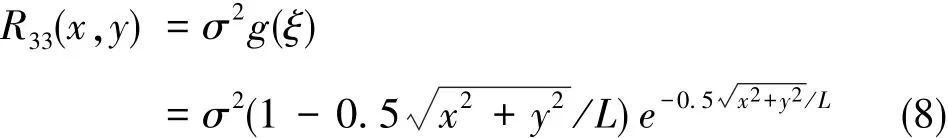
由式（8）可知，二维紊流场不是独立的随机过程，因此必须考虑点（i-1，j-1）。所以，式（4）的算法对于二维紊流风场不成立。

1.3 大气紊流的强度和尺度

根据式（8），可得：

其中，σ是紊流强度均方差，h是采样步长，L是紊流尺度。

（1）强度选择

对于Dryden模型，按照超越概率分等级。例如：1/102概率为轻度紊流风，1/103概率为中度紊流风，1/105概率为严重紊流风。在65000ft（19812m）的海拔高度，标准差超越稳态风速8ft/s（2．5m/s）以上的概率为1/105，所以这个高度的紊流风速强度取为：σwx＝σwy＝2．5m/s。

（2）尺度选择

地面533m以上脉动风尺度取为：

1.4 离散自递归模型

由1．2小节可知，图2中（i，j）点处的紊流值与（i-1，j）、（i，j-1）、（i-1，j-1）这3处的紊流值相关，根据1．1小节中的假设条件，建立二维1阶自递归模型：

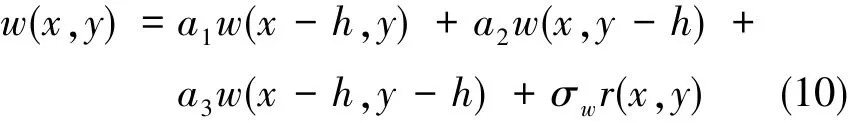
下面给出系数a1、a2、a3、σw的具体算法。

设Rij＝E［w（x，y）w（x+ih，y+jh）］。其中，h是采样步长，i＝0、1、2、…，j＝0、1、2、…。

于是：

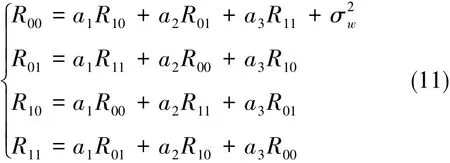
采用Cramer法则求解式（11），得系数a1、a2、a3。

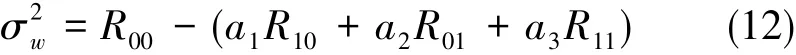
根据式（10）～式（12），结相应的紊流强度、尺度参数值，选择合适的步长，给出维紊流场的局部样本，如图3、图4所示。

由图3、图4可知，紊流的东风分量沿x方向的波动范围是（3m/s，-30m/s），沿y方向的波动范围是（5m/s，-20m/s）；紊流的北风分量沿x方向的波动范围是（-3m/s，-30m/s），沿y方向的波动范围是（-5m/s，-20m/s）。由此看来，扰动风速与飞艇巡航速度15m/s～20m/s相比，量级相当。因此飞艇在平流层风场中运动时，大气紊流的扰动不能忽略，建模要充分考虑风速变化对飞艇运动特性的影响。

2 大气紊流扰动下飞艇动力学模型

2.1 飞艇六自由度方程

为简化推导过程，进行以下基本假设：

1）将飞艇视为刚体，忽略艇体的弹性变形。

2）飞艇的外形和质量分布关于纵平面oxbzb对称，且体积中心和浮心重合。

3）忽略副气囊充放气导致的质量变化。

4）忽略地球旋转及曲率，将地面坐标系近似为惯性坐标系。

上述假设对于区域驻留段和低速巡航段的飞艇而言，基本符合实际情况。

大气扰动飞行原理的最基本关系是速度三角形［2］，地速UK、风速Uw、空速U三者之间有如下关系：

上述3个速度作用在飞艇体积中心，它们在艇体系中的分量为：

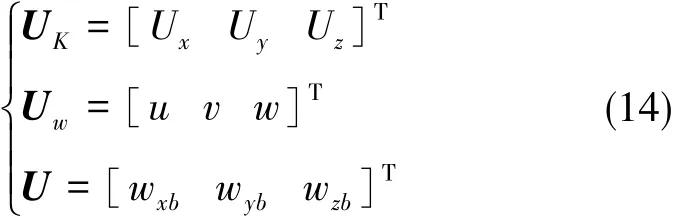
由理论力学知，艇体坐标系中，风场干扰下的非线性飞艇六自由度模型如式（15）所示：

Fx、Fy、Fz是合力沿3个坐标轴的分量，p、q、r是角速度在艇体坐标系中的分量。

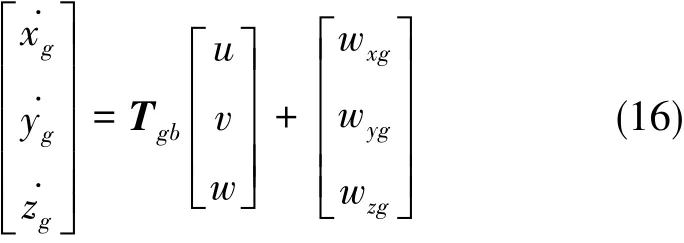
［xgygzg］T是质心在地系中的坐标分量，风速Uw在地系中的坐标分量［wxgwygwzg］T，Tgb为艇体坐标系到地面坐标系的转换矩阵［3］。

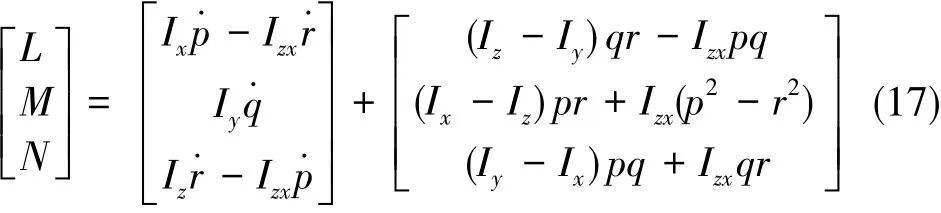
其中，L、M、N是总力矩在艇体坐标系中的分量，Ix、Iy、Iz是惯性矩，Izx是惯性积。

其中，θ、ψ、φ是姿态角。

2.2 水平面内飞艇动力学模型

存在风场扰动时，平流层飞艇在控制系统的作用下，依靠自身动力系统回到指定位置，并长期悬停于某地。因此平流层飞艇主要以水平面内运动为主，即仅考虑飞艇的前向和侧向运动，不考虑竖直方向的运动、滚转俯仰运动［7］。参照潜水艇的建模思路［8］，对2．1小节中建立的飞艇动力学模型进行水平与竖直解耦，得到简化后的水平面内动力学模型如式（19）所示：

3 数值仿真

3.1 配平

要保证飞艇在水平面内做匀速直线运动，则飞艇受到的合力与合力矩均等于0［9］。在此稳定飞行状态下，飞艇无非对称运动（侧力、偏航力矩均为0），侧滑角、方向舵偏角也为0。

3.2 飞艇动力学模型仿真

以某型号飞艇为例，在配平基础上，根据扰动风速自递归模型，采用Matlab和Simulink对随机风场下水平面内飞艇运动模型，进行数值计算。分有风干扰和无风扰动2种情形进行讨论。

由图5可以看出，无风情形下，飞艇在水平面内沿x方向做定直平飞运动，速度大小为20m/s，无侧滑。所以，y方向速度和位移均为0。

图5 无风时飞艇速度、位移响应Fig.5 Speed and displacement response of the airship without wind

图6与图5相比，可以看出，在大气紊流的扰动下，飞艇不再保持20m/s的匀速运动状态，x方向速度分量出现随机波动，y方向速度分量不再是0，波动幅度较大，飞艇产生不稳定的侧滑运动；从图6位移曲线可知，无控制状态下，有风作用时，飞艇运动轨迹较为复杂，不再做匀速直线运动，偏离无风时的既定航线。综上所述，紊流风速对飞艇运动特性影响较大，并且较大的风速使飞艇处于不断的颠簸状态，对艇载设备造成不利影响，所以建立飞艇动力学模型时，必须考虑飞艇所处的外界环境，尤其风场的影响对飞艇运动带来的干扰。

图6 风干扰时飞艇速度、位移响应Fig.6 Speed and displacement response of the airship with wind

4 结论

本文在无风状态下飞行器六自由度方程的基础上，结合风速矢量三角形，推导出大气紊流影响下的飞艇水平面内动力学方程，并根据已有的飞艇气动数据，对飞艇的运动特性进行仿真。结果表明：无风干扰时，飞艇按照既定航线做匀速平飞运动；加上扰动风后，飞艇的运动轨迹出现了较大变化，呈现不稳定的随机波动特性。另外，本文构建的风扰条件下高空飞艇水平面内动力学模型，可为后续平流层飞艇长航时悬停的控制器设计提供一定的依据。

［1］赵震炎，肖业伦，施毅坚．Dryden大气紊流模型的数字仿真技术［J］．航空学报，1986，7（5）：433-443．ZHAO Zhen-yan，XIAO Ye-lun，SHI Yi-jian．The numerical simulation technology for the Dryden model of atmosphere turbulence［J］．Acta Aeronautica et Astronautica Sinica，1986，7（5）：433-443．

［2］王晓亮，单雪雄．飞艇稳定性和能控性分析［J］．计算机仿真，2005，22（8）：40-44． WANG Xiao-liang，SHAN Xue-xiong．The stability and controllability analysis of the airship［J］Computer Simulation，2005，22（8）：40-44．

［3］肖业伦，金长江．大气扰动中的飞行原理［M］．北京：国防工业出版社，1993．XIAO Ye-lun，JIN Chang-jiang．The flight principle about theatmosphericdisturbances［M］．Beijing：National Defense Industry Press，1993．

［4］陆宇平，胡亚海．基于空间相关函数的二维紊流场数值生成法［J］．南京航空航天大学学报，1999，31（2）：139-145．LU Yu-ping，HU Ya-hai．The numerical method based on spatial correlation function of two-dimensional turbulent flow field［J］．Nanjing University of Aeronautics and Astronautics，1999，31（2）：139-145．

［5］乔振宇，杨天祥．飞艇扰动特性的分析方法研究［J］．测控技术，2011，30（11）：114-118．QIAO Zhen-yu，YANG Tian-xiang．Research on analysis method of the airship disturbance characteristic［J］．Measurement and Control Technology，2011，30（11）：114-118．

［6］肖业伦．用于飞行仿真的二维紊流场的数字生成法［J］．航空学报，1990，11（4）：124-129．XIAO Ye-lun．The digital generation method for the flight simulation of two dimensional turbulent flow［J］．Acta Aeronautica et Astronautica Sinica，1990，11（4）：124-129．

［7］李家宁．平流层飞艇定点控制技术研究［D］．南京航空航天大学，2009．LI Jia-ning．The stratosphere airship fixed-point control technology［D］．Nanjing University of Aeronautics and Astronautics，2009．

［8］施生达．潜艇操纵性［M］．北京：国防工业出版社，1995．SHI Sheng-da．The submarine maneuvering［M］．Beijing：National Defense Industry Press，1995．

［9］丁秋峰，陈丽，段登平．低空无人飞艇运动配平和控制器设计研究［J］．系统仿真学报，2009，21（10）：3035-3038．DING Qiu-feng，CHEN Li，DUAN Deng-ping．Research on the low altitude unmanned airship movement balancing and controller design［J］．Journal of System Simulation，2009，21（10）：3035-3038．

Study for the Horizontal Movement of Airship under the Two-dimensional Turbulence

WANG He1，2，LI Zhi-bin3
（1．Beijing Institute of Control Engineering，Beijing 100190；2．Science and Technology on Space Intelligence Control Laboratory，Beijing 100190；3．Academy of Opo-electronics，Chinese Academy of Sciences，Beijing 100094）

Atmospheric turbulence is a key factor that affects airship fixed-point hover．When building the turbulent flow model，the Dryden model based on the spectral decomposition theorem is adopted．But the traditional method only generate one-dimensional atmospheric turbulence model．It is necessary to build two-dimensional atmospheric turbulence model for the complex flight movement of the airship．Firstly，a recursive model of two-dimensional turbulence based on the spacerelated function is adopted to construct the wind field in this paper．Secondly，the dynamic model of the airship under the disturbance of the wind field is built according to the wind velocity triangle relationship．And then the model is decoupled in the horizontal and vertical direction．The simulation results indicate that the forces of wind acting on the airship will make it deviate from the flight trajectory comparing with no wind．Therefore，the paper conforms that turbulence effect needs to be considered when the dynamic model of airship is constructed．

atmospheric turbulence；two-dimensional turbulence；the dynamic model of the airship

V212

A

1674-5558（2017）01-01382

10．3969/j．issn．1674-5558．2017．03．001

王鹤，女，博士，飞行控制专业，研究方向为飞行器设计与控制。

2017-03-28

国家自然科学基金（编号：61273199，61603320）