半球谐振陀螺控制电路频率跟踪精度提升方法

赵万良，王 伟，齐轶楠，荣义杰，李绍良

（1．上海航天控制技术研究所，上海201109；2．上海惯性工程技术研究中心，上海201109）

半球谐振陀螺控制电路频率跟踪精度提升方法

赵万良1，2，王 伟1，2，齐轶楠1，2，荣义杰1，2，李绍良1，2

（1．上海航天控制技术研究所，上海201109；2．上海惯性工程技术研究中心，上海201109）

半球谐振陀螺控制电路的控制精度直接影响半球谐振陀螺仪的输出精度，而频率跟踪精度又直接影响了半球谐振陀螺控制电路的精度。传统的半球谐振陀螺数字控制电路采用过零比较的方法计算陀螺幅点信号的频率，此方法易受地线毛刺信号的干扰，频率跟踪精度不高。介绍了采用A/D转换采集数据估算陀螺幅点信号频率的方法，并对各种方法进行了优缺点比较，提出选用建议。这些方法既提升电路抗干扰能力，又大幅提升了频率跟踪精度，还省去了过零比较电路。分析及测试结果表明，采用该频率跟踪方法，半球谐振陀螺的频率跟踪精度可达0．002Hz，可大幅提升半球谐振陀螺控制电路的精度。

半球谐振陀螺；星载惯性敏感器；频率跟踪精度；控制电路；A/D转换

0 引言

半球谐振陀螺是一种利用半球壳唇缘的径向驻波进动效应来感测基座旋转的一种新型振动陀螺。它无运动部件，内部功耗小，对磁场不敏感，有很高的测量精度和超强的稳定性，抗辐照能力强，非常适合空间航天任务［1-2，7］。在NASA的支持下，利顿公司通过提高分辨率和降低噪声，研制的半球谐振陀螺零偏稳定性达到0．000011（°）/h1/2［3］。国内半球谐振陀螺的研究受制于陀螺加工工艺及控制电路的影响，精度与国外一直有较大的差距。因此，如何提升半球谐振陀螺的精度是国内研究的热点［6］。影响半球谐振陀螺精度的薄弱环节很多，目前提升半球谐振陀螺精度的主要途径是提升其敏感器加工装配精度和控制电路精度。半球谐振陀螺控制电路涉及陀螺信号解调、低通滤波、PI控制等多个环节。陀螺信号解调需要先跟踪陀螺幅点信号的频率（半球谐振陀螺的谐振频率），然后根据谐振频率产生基准频率信号参与陀螺信号的解调。若频率跟踪产生较大误差将使解调信号严重失真，从而直接影响到陀螺控制电路的控制精度。半球谐振陀螺控制电路有模拟和数字之分，对于数字控制电路，高精度的模数转换电路可以提高半球谐振陀螺控制精度［8］。

1 频率跟踪精度对陀螺精度的影响

半球谐振陀螺控制电路涉及幅度、正交、力反馈闭环环路。其中，幅度环路是为保持半球谐振子四波幅的幅度稳定，给谐振子振动补充能量；正交环路是补偿半球谐振子频差对四波幅振型的影响，使四波幅振动保持稳定；力反馈回路是为抵消由于陀螺基座旋转而产生的谐振子四波幅进动，检测出陀螺基座的旋转角速度。3个环路相互耦合相互影响，间接或直接影响陀螺的输出精度［2］。而这3个环路的控制稳定需要对陀螺信号进行精确的解调，图1是半球谐振陀螺幅点解调的基本示意图。频率跟踪器采集幅点信号X的频率，产生一个同频同相的内部信号源Cos_f信号。X信号经A/D采集后与Cos_f信号输入数字乘法器相乘，结果输入低通滤波器产生表征幅度的A信号［4-5］。

半球谐振陀螺解调电路会因为频率跟踪电路没有很好地跟踪X信号的频率，而产生解调误差。在频率跟踪器与X信号的频率偏差0．1Hz、0．01Hz、0．001Hz和没有偏差时解调器的解调输出情况如图2所示。

从图2中可知，在频率跟踪器参数的频率与X信号的频率出现频率偏差时，解调值会出现一定的趋势变化。频率偏差越大，趋势越明显。直到频率偏差小于0．001Hz时，解调值与理想值（频率没有偏差）相当。这些带有趋势变化的解调信号引入闭环控制系统后，由于控制系统的闭环调整功能，闭环系统可以工作，但因解调误差的存在而使控制回路的噪声增加。这些噪声是影响半球谐振陀螺控制精度的根源之一，因此应尽可能提升频率跟踪器的精度，以提升陀螺信号的解调精度。

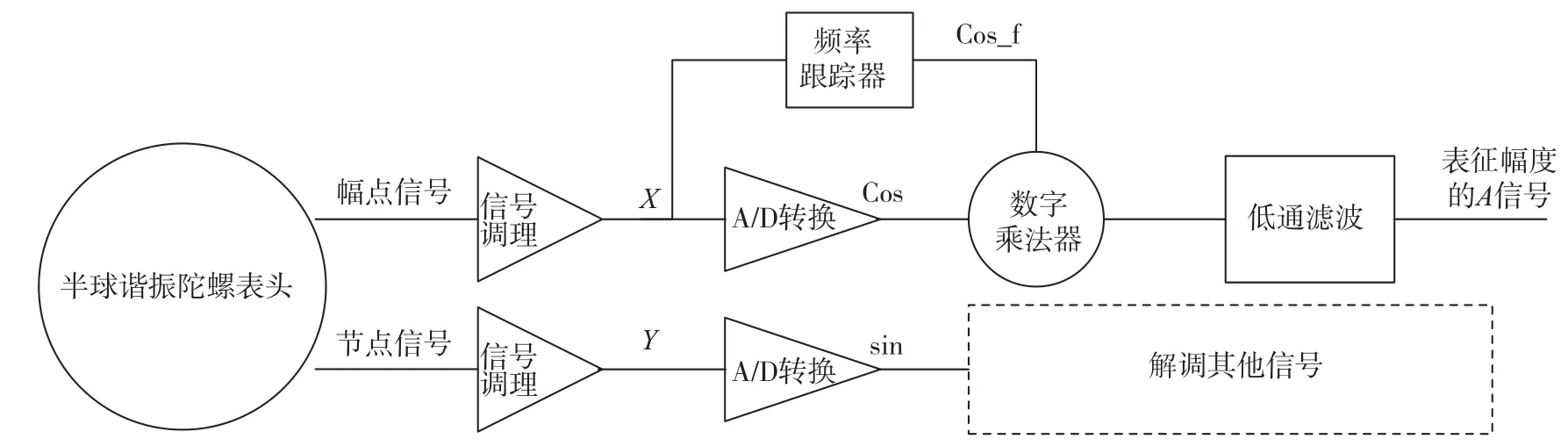
图1 半球谐振陀螺幅点解调示意图Fig.1 Schematic diagram of the amplitude demodulation of the HRGs

图2 频率跟踪器不同频率偏差下解调输出仿真图Fig.2 Demodulation simulation of the output under the different frequency bias

2 半球谐振陀螺控制电路提升方案

2.1 现有频率跟踪器存在的问题

传统的模拟式半球谐振陀螺控制电路的频率跟踪器一般采用正弦过零相位检测方法。此方法也被沿用在数字式半球谐振陀螺控制电路上，如图3所示。

图3 正弦过零相位检测示意图Fig.3 Schematic diagram of the sine zero-crossing phase detection

此方法是通过电压比较器对半球谐振陀螺幅点信号X进行过零比较，产生方波信号，然后用FPGA对方波信号的上升沿（或下降沿）进行检测，计算2个上升沿（或下降沿）的时间T，然后通过周期T与频率f的计算公式计算出正弦信号的频率（该方法称为方法1）。

半球谐振陀螺幅点信号是以0V电压为中心电平，比较器对地电位进行比较而得出X信号的过零点，因此电压比较器负端接地。若电压比较器负端出现一个毛刺型干扰信号，且该干扰信号正好在正弦信号过零附近，比较器很容易误触发，从而导致上升沿（或下降沿）比正弦信号实际过零要提早或推后，造成信号检测误差。如图4所示，Δt为因地噪声造成的电压比较器超前触发的时间。

为避免电压比较器对地噪声太过敏感，一般需要对电压比较器增加迟滞比较环节，迟滞比较器的时延TD需要精心设计。若TD时间设计太短，地线上的毛刺很难滤除；若TD时间设计太长，又将影响信号检测精度。若半球谐振陀螺幅点信号X频率为fx，则该频率跟踪器的相位跟踪精度Δδ为：

高速的A/D转换及D/A转换功耗大，不能满足要求，故半球谐振陀螺控制电路一般考虑A/D转换及D/A转换的转换频率都在500kHz左右。故电压比较器的迟滞比较器应避开500kHz以上的频率，TD时间应大于2μs。为描述本频率跟踪器的最好相位跟踪精度，TD时间取2μs，半球谐振陀螺的谐振频率取5000Hz，代入式（1），则此方法可以检测的频率精度是3．6°。该频率跟踪器的相位误差将给解调信号带来极大的噪声。

2.2 频率跟踪器精度提升的方法

半球谐振陀螺控制电路本身采用A/D转换器采集幅点信号X，X信号为正弦信号。本文提出一种用A/D转换器采集的值直接计算正弦信号相位的方法，如图5所示。

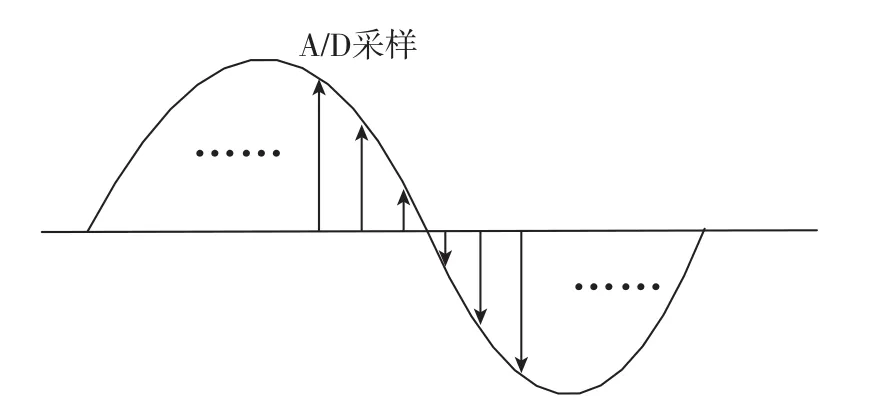
图5 A/D转换器采集值直接计算正弦信号相位示意图Fig.5 Phase diagram of the sine signals by the A/D convertor collection

当A/D采样的值由正值变为负值（或由负值变为正值）时，因A/D转换器采集频率比幅点信号X高得多，故可以把A/D转换2个相邻采样点的正弦信号拟合为一条直线。记过零前的A/D采样数值为A，过零后的A/D采样数值为B，如图6所示。正弦曲线通过直线等效后根据A、B的数值的大小估计过零点的时刻，使用式（2）即可计算正弦信号的过零点时刻，然后通过正弦信号一个周期的时间计算出正弦信号的频率（该方法称方法2）。

图6 正弦曲线过零检测示意图Fig.6 Schematic diagram of the sine zero-crossing detection

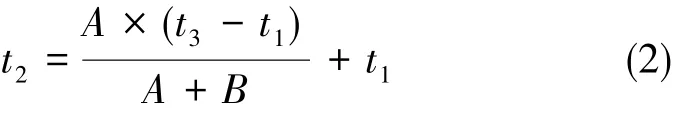
因A/D转换器采集频率比幅点信号X高2个数量级，正弦信号近似为直线带来的误差可以忽略。若A/D转换位数为D，A/D转换位数误差A点和B点各为1LSB，A/D转换时间为Tad且等间隔。通过此方法频率跟踪器的相位跟踪精度为：

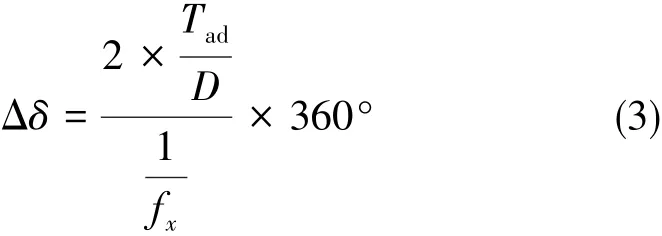
假定A/D转换器为14位，A/D转换器采集频率为500kHz且等间隔，那么对过零点的时间跟踪精度为0．001757°。

方法2实现了频率跟踪器高精度相位检测的功能，然而因幅点信号过零时A/D采集的数值很小，若地线噪声没有处理好地线毛刺仍可能被A/D转换采集，而误认为是幅点信号的过零点。针对该问题提出2个改进方法。

方法3，FPGA软件处理法。

因半球谐振陀螺幅点信号即谐振子的谐振频率，谐振子采用高纯熔融石英加工而成，有超强的稳定性，谐振子谐振频率不可能突变，可以通过FPGA软件算法把因干扰信号而计算出的错误周期信号剔除。比如，对方法2计算的正弦信号周期T进行去最大值和去最小值处理后，再取平均值。在软件算法设计好的情况下，该方案可保持与方法2同样的跟踪精度。

方法4，避开干扰信号方法。

方法3需要增加软件算法，将增加FPGA逻辑资源。如在FPGA资源紧张的情况下，方法2还可以在A/D转换采集点选取上进一步优化。考虑到地噪声不可能很大，可以取正弦信号过零点附近比地噪声幅值大的一小段范围内的曲线近似等效为一条直线。设过零前后幅值超过地噪声的A/D转换值为C点和D点，如图7所示。

图7 过零算法优化示意图Fig.7 Schematic diagram of the zero-crossing optimization

正弦信号的过零时刻为：

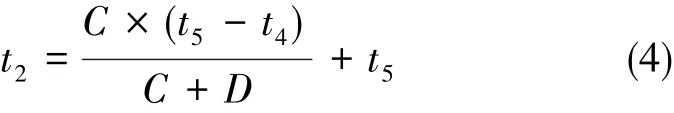
通过本改进的方法不会受地线毛刺干扰的影响，与方法2相比仅增大了因正弦曲线拟合成直线而引入的误差，但因地线干扰幅值本身不大，该方法同样可以保证很高的相位跟踪精度，但具体精度需要根据C、D点的具体值才能计算。

2.3 各种方法比较及选用建议

比较4种方法，可以得到如表1所示的各个方法的优缺点。

方法1虽然频率跟踪差，但因不需要数字电路的支持非常适合在模拟式半球谐振陀螺控制电路中使用；方法2适用于信号幅值比较大、地噪声比较小的使用场合；方法3频率跟踪精度高，抗干扰能力强，但需要耗费FPGA资源，在控制电路中使用的FPGA资源充足的情况下是首选方案；方法4比方法3跟踪精度差，但不需耗费更多的FPGA资源，在控制电路中FPGA资源紧张的情况下是首选。经在半球谐振陀螺控制电路实验验证，在地噪声不大的情况下，方法3和方法4实际效果差别不大，比方法1的频率跟踪精度提升3个数量级左右。在地噪声较大的情况下设计好软件算法，方法3比方法4精度高，但FPGA资源耗费相对较大，需要进行工程折中。

表1 各种频率跟踪方法比较Table 1 Comparison of the different frequency tracing methods

实验中所用的相位采样速率为390625Hz。

图8所示为方法1模拟过零比较法频率跟踪方式上传所得的相位步进值，可得频率采样精度为：38502×（390625/228）≈56Hz。但由于信号每周期都会更新频率，并实时计算相位，从长时间看仍能跟踪信号频率，保证半球谐振陀螺控制电路的闭环工作。

图9所示为方法2正弦曲线过零估计相位步进，可得频率采样精度为：3011×（390625/228）≈4Hz。

图8 模拟过零比较法相位步进Fig.8 Phase step of the analog zero-crossing comparison

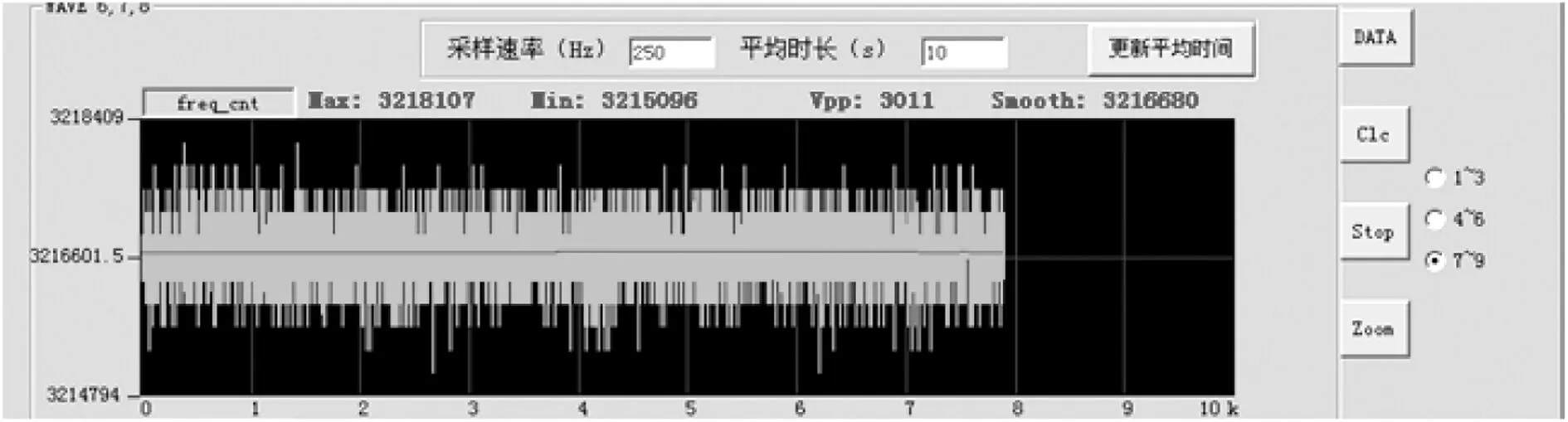
图9 正弦曲线过零估计法相位步进Fig.9 Phase step of the sine zero-crossing estimation

图10所示为方法3多周期均值相位步进。这种方法通过多周期平均以消除干扰，可以达到设计的频率跟踪精度，即1×（390625/228）≈0．0015Hz，但此方法只适用于温度变化小或基本恒定，从而半环谐振陀螺频率变化也缓慢的场合。

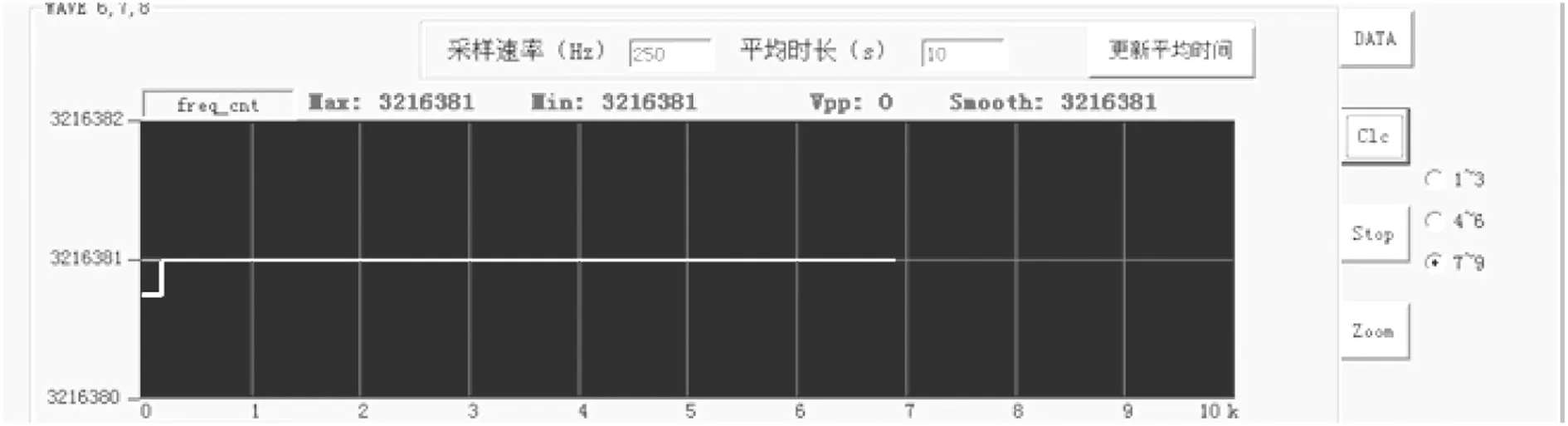
图10 多周期均值法相位步进Fig.10 Phase step of the multicycle mean value

3 结论

本文介绍了采用A/D转换器采集的值估算陀螺信号频率的高精度频率跟踪精度的方法，这些方法既省去了过零比较的硬件电路，又能大大提升半球谐振陀螺控制电路频率跟踪精度。通过对各种方法的比较，给出了各种方法的适用场合。分析及测试结果表明，采用A/D转换器采集的值估算频率的方法比传统的电压比较器过零比较法相位跟踪精度提升了3个数量级，精度可达0．002Hz，可大幅提升半球谐振陀螺数字控制电路的解调精度。

［1］周强．半球谐振陀螺模型分析与控制电路技术研究［D］．电子科技大学，2009．ZHOU Qiang．Study on model analysis and control circuit of the HRG［D］．University of Electronic Science and Technology of China，2009．

［2］雷霆．半球谐振陀螺控制技术研究［D］．重庆大学，2006．LEI Ting．Study on control technology of hemispherical resonator gyro［D］．Chongqing University，2006．

［3］吕志清．半球谐振陀螺在宇宙飞船上的应用［J］．压电与声光，1999，21（5）：349-353．LV Zhi-qing．The application of HRG in the spacecraft［J］．Piezoelectric＆Acoustooptics，1999，21（5）：349-353．

［4］李云．半球谐振陀螺力再平衡数字控制技术［D］．国防科学技术大学，2011．LI Yun．Digital control technology for force to rebalance mode hemispherical resonator gyro［D］．National University of Defense Technology，2001．

［5］吕志清．半球谐振陀螺（HRG）信号处理技术［J］．中国惯性技术学报，2000，8（3）：59-62．LV Zhi-qing．Signal processing technique for hemispherical resonant gyro（HRG）［J］．Journal of Chinese Inertial Technology，2000，8（3）：59-62．

［6］齐轶楠，赵辉，赵万良，等．半球谐振陀螺组合零偏稳定性提升技术研究［J］．导航定位与授时，2015，2（6）：63-68．QI Yi-nan，ZHAO Hui，ZHAO Wan-liang，et al．Research on the technology of improving the zero-bias stability of the hemispherical resonator gyroscope unit［J］．Navigation Positioning＆Timing，2015，2（6）：63-68．

［7］赵万良，荣义杰，齐轶楠，等．星载半球谐振陀螺惯性敏感器研究进展［C］．中国惯性技术学会第七届学术年会，2015：337-341．ZHAO Wan-liang，RONG Yi-jie，QI Yi-nan，et al．Research progress on the satellite borne HRG［C］．7thAnnual Academic Conference of Chinese Society of Inertial Technology，2015：337-341．

［8］齐轶楠，赵辉，赵万良，等．半球谐振陀螺组合高精度模数转换技术研究［C］．中国惯性技术学会第七届学术年会，2015：6-9．QI Yi-nan，ZHAO Hui，ZHAO Wan-liang，et al．Highprecision analog-digital conversion technology research of hemispherical resonator gyro assembly［C］．7thAnnual Academic Conference of Chinese Society of Inertial Technology，2015：6-9．

Approach to Improve the Frequency Tracking Accuracy of the HRG Control Circuit

ZHAO Wan-liang1，2，WANG Wei1，2，QI Yi-nan1，2，RONG Yi-jie1，2，LI Shao-liang1，2
（1．Shanghai Institute of Spaceflight Control Technology，Shanghai 201109；2．Shanghai Engineer Research Center of Inertia，Shanghai 201109）

The accuracy of the hemispherical resonant gyroscopes（HRG）is affected by the control circuit accuracy directly，and the control circuit accuracy is affected by the tracking frequency accuracy．The frequency of the gyroscope's amplitude is calculated by the zero-cross detection in the traditional HRG control circuit．Effected by the undesired signal noises from the ground electrode，the frequency tracking is not accurate．The method to estimate the resonant frequency by the A/D convertor was proposed in this paper．And the different solutions following this method are compared to show their merits and demerits．These solutions，not only increase the interference immunity of the HRG，but also simplify the circuits．It is shown that，by using these methods，the tracking frequency accuracy could reach 0．002Hz by the test and analysis，which could improve the control circuit accuracy of the HRG significantly．

hemispherical resonant gyroscope（HRG）；satellite borne inertial sensor；frequency tracking accuracy；control circuit；A/D convertor

V241．5+54

A

1674-5558（2017）02-01307

10．3969/j．issn．1674-5558．2017．03．009

赵万良，男，硕士，高级工程师，研究方向为星载惯性敏感器技术。

2016-08-12