“用字母表示数”的历史演进及其数学价值

◇刘爱东

在数学发展的历史长河中，从具体的量抽象出一般的数，是第一次抽象；随着生产的发展、生活的需要，第一次抽象出来的数不够用了，必然会引起数学史上的第二次抽象，即由自然的“算术语言”走向抽象的“代数语言”。“用字母表示数”是由“算术语言”向“代数语言”过渡的起始，是学生学习代数的入门知识，也是学习方程、不等式等内容的重要基础，它打破了从“确定的数”到“不确定的数”之间的壁垒，实现了由算术向代数的重大跨越。“用字母表示数”的发展大致经历了三个主要阶段，即文辞代数阶段、缩略代数阶段和符号代数阶段。

一、“用字母表示数”的历史发展

1.文辞代数阶段。

文辞代数亦称修辞代数，通常是指在代数学发展的早期，人们还不会使用符号表示未知数，所有的问题完全靠语言文字来表达和解决，因此，文辞代数阶段要表述清楚一个代数问题，往往会用文字写成长长的一段。

最早的代数被发现于苏美尔人的黏土片（约公元前3000年）上，最早的代数语言是古巴比伦人（约公元前1900年）在使用苏美尔人的旧教材过程中产生的。古巴比伦人常用 “us”（长）、“sag”（宽）、“asa”（面积）这些字代表未知量，比如他们的“我把长乘宽得面积10，问长和宽分别是多少”，就相当于现在的xy=10。显然，这里的未知量“长、宽”，已知量“面积 10”，并不一定是它们原来所代表的几何量，只不过是两个未知量及其乘积的简便说法。而古埃及人把未知数用“堆”（hau）表示，意思是一堆不知道多少数量的谷物。他们在数学著作《兰德纸草书》（约公元前1650年）中，论及食品和其他东西分配的问题时，出现了简单的方程，如：“有一堆，加上它的、它的和它的，共为33，求该量。”

到了古希腊时期，毕达哥拉斯学派（公元前6世纪）的数学家们研究了多边形，由于他们仍然在确定的数的范围内进行研究，不知道用字母表示数，所以对于某一个具体的多边形数，他们可以十分清楚地表述，但对于“任一三角形数”“任一正方形数”等表示一类的量，却无法用统一的文字表述，更不会有“任意多边形数”的表达。即便是大数学家欧几里得，虽然在其所著的《几何原本》（公元前3世纪）中，把线段的名称用一个或两个字母表示，但他同样不会用字母表达“任意多个”，依然只能用烦琐的文字来说明其观点。如对命题“若将几个偶数相加，则其和为偶数”的证明：“设把几个偶数AB、BC、CD、DE相加，则可证其和AE为偶数。因为，数AB、BC、CD、DE中的每一个都是偶数，则它们可被二等分，这样，其和AE也可二等分，但可以二等分的数为偶数，所以AE为偶数。”可见，在证明的过程中，欧几里得只能用4个偶数来代替“几个偶数”，只能反复使用偶数的原始定义进行证明，只能用冗长的几何语言来表达等式2K1+2K2+…+2Kn=2(K1+K2+…+Kn)。

公元820年左右，阿拉伯数学家花拉子米写了一本书《代数学》，书名直译是“还原与对消的科学”。在书中，花拉子米引入了“还原”“对消”等解方程的专门术语，但他依然是用文字表述解方程的过程，如：“把一个正方形的面积加上其一边长度的10倍等于39时，此正方形的边长是什么？”（即x2+10x=39，求x）他的解答为：“把所加边长的倍数除以2得5。把该数自乘，得乘积25。把此数与39相加，得64。取此数的平方根得8，从该数中减去边长倍数之半剩下3，此即所求正方形的边长。因而所求正方形面积等于9。”直到13世纪初，意大利数学家斐波纳契在《计算之书》中，仍然是用文字来说明二次幂和的求法。甚至16世纪的意大利数学家塔塔里亚，为了不让自己遗忘所发现的、用语言叙述的三次方程的求根公式，费尽心机，自编长诗帮助记忆……没有字母的代数，叙述起来是多么的不容易啊！

2.缩略代数阶段。

缩略代数又称缩写代数，以引入字母表示数为典型特征，是指用相应词语的缩写字母来简化文字叙述运算，以使代数的思路和书写更加紧凑、更加有效。

公元250年左右，希腊数学家丢番图在著作《算术》中，首次创造并使用了一套缩写符号，用来简化文字叙述运算。比如用p代表plus（加）,m代表minus(减)等，特别是用符号ξ来表示未知数并用于计算，是摆脱文辞代数的束缚进入缩略代数阶段的标志。因为，在用字母表示数的希腊计数制度中，字母α、β、γ…表示的都是已知自然数1、2、3…，只有字母ξ还没有用来表示自然数。丢番图把未知数称为“未确定单位的数”。用字母来表示未知数这一思想的确立，无疑使代数学前进了一大步。到了公元7世纪，印度数学家和天文学家婆罗摩笈多也创造了一套表示未知数的符号，与丢番图不同的是，他用梵文颜色名的首音节来表示未知数。比如，用 Yavat-tavat（多少）的首音节Ya表示第一未知数等，这套符号虽然不多，但与丢番图的缩写符号相比，显然更具实用性。

在中国，早在秦汉时期的数学家们为了编制历法，就已经开始对一些方程进行研究，那时的人们用“天、上……、仙”九个字分别表示未知数的正幂，用“地、下……、鬼”九个字表示负幂，用“人”表示常数项。以后经过简化，到了1248年，金代数学家李冶在其著作《测圆海镜》中，系统论述了一种用数学文字符号列方程的方法——天元术，明确用 “天元”表示未知数一次项，“立天元一为未知数”相当于现在的“设未知数为x”，用天、地表示未知数的正次幂和负次幂，规定正幂在上，常数和负幂在下。在天元术中，多项式用分离系数法和位值制表示：在一次项旁记一“元”字或在常数项旁记一“太”字，其他项的幂次视与“元”或“太”的相对位置而定，如图1表示的多项式是x3+336x2+4184x+2488320=0。天元术列方程的方法和现代列方程的方法相一致，欧洲数学家直到16、17世纪才做到这一点。

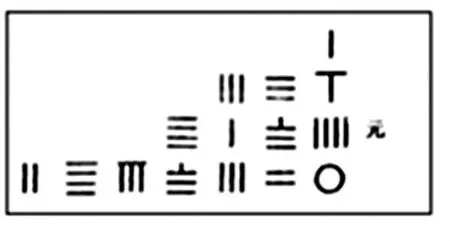
图1

丢番图、婆罗摩笈多、李冶等数学家用缩写的字母或文字来表示未知数，推动了代数学的发展。但正是因为他们是用缩写的方法解题，所以每一个方程都只能按照其本身的特点和细节，用特殊的字母代替题中的已知数，导致每一道题都只能有一种特殊的解法。因此，丢番图解方程是一题一法，有人说：“即便你看懂了他解100个方程的方法，但还是不知道怎样解第101个方程。”婆罗摩笈多关注的也只是对应颜色表示的未知数是什么，而不是未知数之间的一般关系。因此，他们只是在字母表示数的类型与方程解的一般性上做出了贡献，还没有达到用字母表示数的最一般的规律，即“一般量”或“一类量”（任意的已知量或未知量）的高度。

3.符号代数阶段。

16世纪，法国数学家韦达受战场上破译密码的启发，在积累前人经验的基础上，有意识地、系统地使用字母表示数，实现了代数学最重大的历史性的突破。1591年，在他的成名作《分析方法入门》一书里，引入元音字母A、I、O等表示未知数，辅音字母B、C、D等表示已知数。同年，韦达在《美妙的代数》一书中，用字母符号表示未知数，和已知数进行运算，从而把算术和代数加以区别。他在书中写道：“本书将辅以某种技巧，通过符号来区分未知量和已知量，这就是一种永久性质的、易于理解的符号体系。”他不仅用字母表示未知量和已知量的乘幂，而且用来表示一般的系数。韦达将这种新的代数称为“类的算术”，以区别于旧的“数的算术”，从而使代数一下子成为研究方程的普通方法。

韦达之后，法国数学家费马用字母表示曲线方程，大写元音字母表示变量，大写辅音字母表示常量。1637年，法国数学家笛卡尔认为韦达创造使用的未知量和已知量符号不够简洁明快，在他的里程碑式作品《几何学》(1637)中，采用小写字母，并将字母表中靠前的字母，如a、b、c等表示已知数或常量，靠后的字母x、y、z等表示未知数或变量，初步建立了代数符号系统，发展成为今天的习惯用法。但韦达、费马和笛卡尔所用字母表示的数，都是表示正数。1657年，荷兰数学家赫德首先提出字母既可以表示正数，又可以表示负数。从此以后，数学家历经两千多年努力所创造的用字母表示数的方法，便贯穿于全部数学中。由此，数学在表达方法、解题思想和研究方法方面都发生了深刻的变化。有了字母表示数，代数学中的代数式、代数方程便出现了。

二、“用字母表示数”的教学价值

1.根据历史相似性促进数学思维的提升。

数学发展史告诉我们，用字母表示数的过程，不是简单的用字母代替文字的过程，而是具体数量符号化的过程。孩子们的认知发展可能各具特点，但总体上不会违背人类认识提升的一般规律。因而，认识用字母表示数存在这样的递进关系：字母不仅可以表示未知数，还可以表示已知数；字母不仅可以表示特定意义的数，还可以表示变化的数；不仅可以在缩写水平上运用字母，还可以在符号水平上运用字母。在实际教学中，只有真正让孩子理解字母的符号概括作用，理解字母表示的是“一类量”的思想，他们的认识才能超越算术走向代数，实现质的飞跃。

2.在知识形成过程中凸显数学的本质。

《教师教学用书》中，往往把用字母表示数表述为 “是人类认识由具体到抽象的一次飞跃”，而对于为什么说是人类认识的飞跃，其中突破了什么，是什么形成了突破，又以什么为突破的标志等问题都没有作进一步的阐释。战略性的数学概念，仅仅看它最终形式化的或是数学价值的表述，很难深入把握其确切的本质意义，只有把这些问题都搞清楚，才算是在经历知识形成的过程中触摸到数学的本质。比如，教学中要有意识地引导学生区别缩略代数表示与符号代数表示的不同：丢番图和韦达都是用字母表示数，而且丢番图明明要比韦达早1200多年用字母表示数，但为什么偏偏韦达被称为“近代代数学之父”？在体会和辨析两者间有什么根本性不同的过程中，体会字母如同符号一样，没有任何具体的意义，体会用字母表示的不再是一个特定的数，不再是表示一个特定的未知量，而是表示一类任意的已知量和未知量。把这些思考弄清楚了，也就明白了教学的关键。

[1]汪晓勤，樊校.用字母表示数的历史[J].数学教学，2011（9）：24-27.

[2]徐品方.数学趣史[M].北京：科学出版社，2013：81-83.

[3]蔡宏圣.数学史走进小学数学课堂：案例与剖析[M]．北京：教育科学出版社，2016：18-35.

[4]蒲淑萍，汪晓勤.学生对字母的理解：历史相似性研究[J].数学教育学报，2012（6）：38-42.

[5]赵丽丽.代数学的符号化进程[J].新课程，2011（1）：110-112.