构建数学模型，培养数学思维——“数图形的学问”教学实录与评析

◇执教/夏丽娟 评析/颜 丹

教学内容：北师大版教材四年级上册“数学好玩”中的“数图形中的学问”。

教学过程：

一 自主互助，初建模型

数学模型，是用数学的语言讲述现实世界中的故事，强调在建立模型的过程中，让学生感悟如何用数学的语言和方法描述一类现实生活中的问题。它不仅为数学表达和交流提供有效途径，也为解决现实问题提供重要工具，帮助学生准确、清晰地认识、理解数学的意义。夏老师这节课中，涉及的鼹鼠钻洞、单程车票、握手等问题，主要构建的是一种线段模型。

（一）理解问题含义。

教师出示鼹鼠钻洞问题（如图1）：

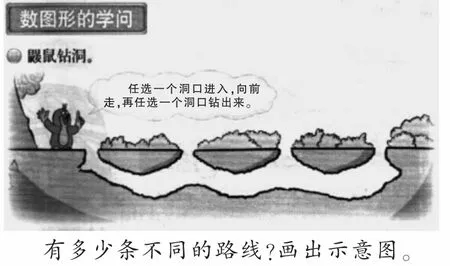
图1

师：在这个问题里，你觉得我们应该关注哪一个词语？

生：进入和钻出。

生：路线。

生：任选。

师：大家说得有一定道理，再找找，看还有没有新的发现？

生：示意图。

师：示意图就是画线段图。我觉得要关注“向前走”，为什么要关注这个词呢？

生：如果不是向前走，别人就认为是往回走。

师：我们关注“向前走”是为了研究方便，只研究一个方向。如果我们既考虑向前走又考虑向后退，问题就比较复杂了。

师：为了研究方便，我们用字母表示洞口（在4个洞口处自左至右依次标注A、B、C、D），用线段表示它们进出的路线。我想请一位同学说说，你认为鼹鼠可能怎么走？

生：从洞口A进，再从洞口B出。

师：就是A进B出，我们就走AB线。

【评析】教师将“鼹鼠钻洞”这一复杂问题简化为线段模型，并带领学生通过研究关键词来分析问题，只考虑单向的线段模型，以降低解决问题中的难度。同时，教师引导学生使用简洁的语言表述，促使自己的思路更清晰地被听者理解，意在培养学生重要的数学思维与表达能力：简洁、明了。

（二）明确学习要求。

师：请一位同学读一下小组合作要求。大家注意听，看哪些词语比较重要。

学生朗读合作学习要求：

1.独立思考，在1号题图上画出示意图，并记录所画路线的条数。

2.在小组内交流自己的画法，介绍每一个数表示的含义。重点介绍怎么样做到不重复、不遗漏。

生：我认为“不重复、不遗漏”很重要。

师：在数学学习中，要有严谨的态度和缜密的思维，它能让我们在生活中胜任精细的工作。

【评析】“有规律地数，不重复、不遗漏”是本节课的重点，小组合作前，教师有意强调这一点，以引起学生的重视，使小组合作在有明确要求的情况下进行，保证合作的有效性，也为后面的有序研究问题作好铺垫。

（三）汇报小组画法。

学生共有如下的画法，如图2所示，针对学生的画法，引导学生展开讨论。

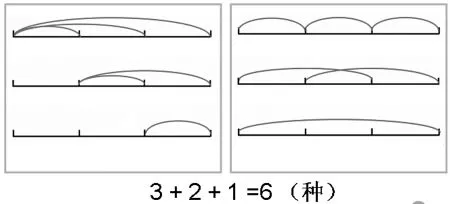
图2

师：明明有4个洞口（如图3），我以为从洞口A进就应该有4条路线，怎么是3条路线呢？

图3

生：因为从点A进，不可能从点A出。

生：用连线的方法，点A不可能和点A连线，除掉它自己，只剩下3个洞口，所以有3条。

生：从点B进（如图4），从其他点出，有两条。

图4

师：怎么就少了一条呢？

生：因为它只能往前走。

师：如果站在连线的角度，还有什么原因？

生：因为点A刚才已经跟点B连了。

师：对，站在连线段的角度来说，A跟B连就等于B跟A连了。

【评析】为了启发学生思考，教师有意抛出自己心中的疑惑，直观在学生面前展示“看似4实则3”的所以然。同时，数学课堂还应有数学味，通过提醒AB和BA是同一条线段，唤醒学生的记忆，这样就顺利联系新旧知识，使学生后面的连线操作做到不重复。

二 释疑深化，简化模型

引导学生探索模型构建的过程，是帮助学生积累数学活动经验的有效途径，但这样的教学需要给学生更多的时间和空间，同时，还需要教师适时引导学生对画法进行优化以达到简化模型的目的。

师：你们把所有的情况都画出来了吗？

图5

生：没有。我们是从点A出发，共画了4条（如图 6）。

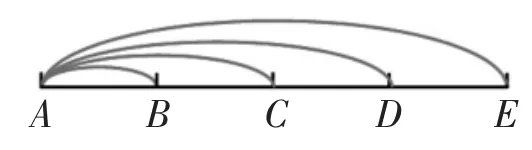
图6

师：想一想，共有几个车站？

生：5个车站。

生：她从点A出发，画了4条路线。

师：是不是说明总共只有4条路线？

生：不是，因为还有从点B出发。

师：你要不要画呢？

生：不需要画，因为点A画完后理应从点B出发，一直往后。

当然，一个省份篮球事业的发展，不单靠一个俱乐部就能完成。广东是全国唯一一个拥有三支CBA球队、一支WCBA球队的省份。宏远队拿过8个CBA总冠军，而在去年举行的天津全运会上，广东篮球在男女成年组、青年组以及三人篮球项目中一共斩获三金、一银和一铜。

生：从点B出发会有3条路线。

生：从点C出发有2条路线。

生：从点D出发有1条路线。

生：我明白了，我们只要把第一点画出来，其他的就不用画了。

生：老师，我发现可以用算式表示，就是4+3+2+1=10。

……

师：如果有6个车站呢，还需要画吗？

生：不需要画了，可以列个算式计算。

师：6个车站，列出算式是5+4+3+2+1=15。7个车站呢？

生：算式是6+5+4+3+2+1。

师：100个呢？

生：从 99加到1，就是 99+98+…+1。

师：n个车站呢？

生：从n-1那个数一直加到1。

【评析】由少画到数，再由数到不数，只需心中有一个数，就能轻松解决问题。从简单问题入手，发现规律后再解决复杂问题，把问题化难为易，这正是数学中重要的研究方法：归纳。教师深入浅出地渗透学习方法，不断地强化学生的数学思维。