2015年高考福建理科卷压轴试题解法探究
——洛必达法则在压轴题中的解题应用
2017-05-17福建省泉州实验中学362000李仲青
福建省泉州实验中学(362000) 李仲青●
2015年高考福建理科卷压轴试题解法探究
——洛必达法则在压轴题中的解题应用
福建省泉州实验中学(362000)
李仲青●

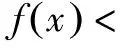
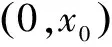

解析 (Ⅰ)(Ⅱ)略.

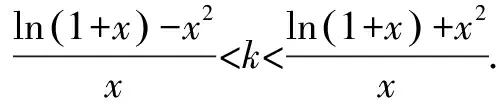
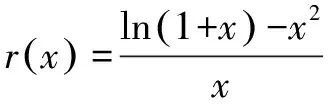



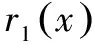
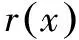

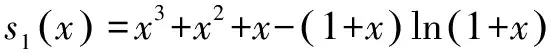
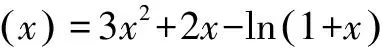

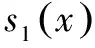

由洛必达法则得,
故k≤1.
由①②可得,k=1.

笔者在近年的全国卷的高考试题中寻得数例,有兴趣的读者可以动手验证,尝试用此方法进行求解.

(Ⅱ)若当x≥0时f(x)≥0,求a的取值范围.
解析 (Ⅰ)略.
(Ⅱ)由x(ex-1)-ax2≥0,可得ax2≤x(ex-1).
(ⅰ)当x=0时,不等式恒成立.

又由洛必达法则得,

>1,因此a≤1.
综上述:a≤1.
(Ⅰ)求a、b的值;
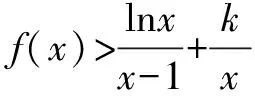
解析 (Ⅰ)易得a=1,b=1.




当0
所以当0
由洛必达法得,
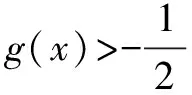
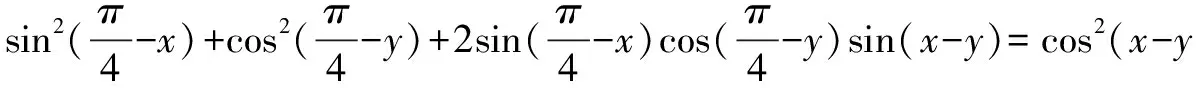
点评 巧妙地构造和差对偶式解题,达到了化繁为简、化难为易的效果.

解 设M=cos1°+cos2°+…+cos44°,
构造对偶式N=sin1°+sin2°+…+sin44°.
则M+N=(cos1°+sin1°)+(cos2°+sin2°)+…+(cos44°+sin44°)
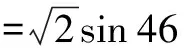

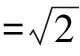
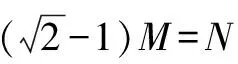
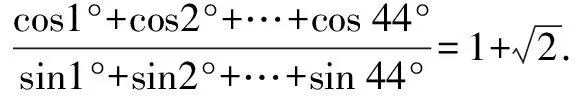
点评 充分利用式子的特征,巧妙地构造出对偶式,利用解方程的思想解决未知数,从而使问题得以顺利解决.
三、证明恒等式
例5 求证:cos2α+cos2β-2cosαcosβcos(α+β)=sin2(α+β)
证明 设M=cos2α+cos2β-2cosαcosβcos(α+β).
构造对偶式N=sin2α+sin2β+2sinαsinβcos(α+β)
则M+N=2-2cos2(α+β)=2sin2(α+β). (1)
M-N=cos2α+cos2β-2cos(α+β)cos(α-β)
=cos[(α+β)+(α-β)]+cos[(α+β)-(α-β)]-2cos(α+β)cos(α-β)=0. (2)
由(1)+(2)得 2M=2sin2(α+β),
即M=sin2(α+β),
原式得证.
例6 在三角形ABC中,求证:cos2A+cos2B+cos2C+2cosAcosBcosC=1.
证明 设M=cos2A+cos2B+cos2C+2cosAcosBcosC,
构造对偶式N=sin2A+sin2B+sin2C+2sinAsinBcosC
则M+N=3+2cosC(sinAsinB+cosAcosB)=3+2cosCcos(A-B)

M-N=cos2A+cos2B+cos2C+2cosCcos(A+B)
=cos2A+cos2B+(2cos2C-1)-2cos2C=cos2A+cos2B-1. (2)
由(1)+(2)得 2M=2,即M=1,
原式得证.
点评 例5与例6都是构造异名对偶式,将sinα与cosα互换,充分运用三角公式进行运算和化简,从而达到了简捷、高效的解题目的.
四、证明不等式
例7 求证:2sin4x+3sin2xcos2x+5cos4x≤5.
证明 设M=2sin4x+3sin2xcos2x+5cos4x,
构造对偶式N=2cos4x+3cos2xsin2x+5sin4x.
则M+N=7(sin4x+cos4x)+6sin2xcos2x=7(sin2x+cos2x)2-8sin2xcos2x
=7-2sin22x=5+2cos22x, (1)
M-N=3(cos4x-sin4x)=3(cos2x+sin2x)(cos2x-sin2x)=3cos2x. (2)
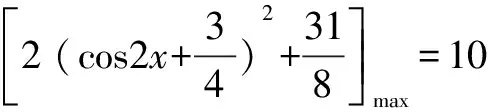
原式得证.
点评 此题若采用降幂或化同名三角函数的思路证明就非常困难,而根据对称的思想构造了一组对偶式来进行证明,解题过程就显得简洁明了.
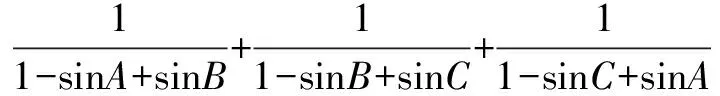

构造对偶式,N=(1-sinA+sinB)+(1-sinB+sinC)+(1-sinC+sinA).
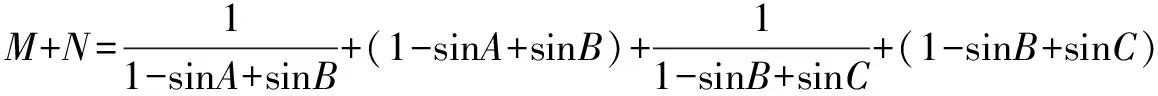

(当且仅当 sinA=sinB=sinC即A=B=C时等号成立)
又因为N=3,所以M≥3.故
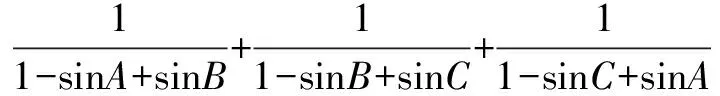
点评 巧妙地构造出与之匹配的倒数对偶结构式,合理、妥善地运用基本不等式获得了较为简捷的解答.
五、解方程

解 设M=cos2x+cos22x+cos23x,
构造对偶式,N=sin2x+sin22x+sin23x.
则M+N=3, (1)
M-N=cos2x+cos4x+cos6x=cos(3x-x)+cos(3x+x)+(2cos23x-1)
=2cos3xcosx+(2cos23x-1)
=2cos3x(cosx+cos3x)-1

=4cosxcos2xcos3x-1. (2)
由(1)+(2)得 2M=4cosxcos2xcos3x+2.又M=1

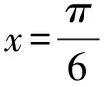
点评 通过构造对偶式,把原方程转化为cosxcos2xcos3x=0这一美妙而又简单的有利条件,使问题得到了圆满解决.
G632
B
1008-0333(2017)10-0008-02
