高考数学选择题巧解八法
2017-05-17山东省文登第一中学264400侯宇虹
山东省文登第一中学(264400) 崔 文● 侯宇虹●
高考数学选择题巧解八法
山东省文登第一中学(264400)
崔 文● 侯宇虹●
选择题是高考数学试卷中的一种常规题型,具有“四选一”,信息量少,分值高的特点.在解答时要科学地选择一定的技巧,做到“少算”,甚至“不算”,以提高解题速度,保证解题质量.
一、代入法
代入法就是将各个选择支分别作为条件,去验证命题,能使命题成立的选择支就是应选的答案.这种方法适合于因果关系明显,代入运算简便的题目.


二、筛选法
筛选法就是根据高考数学选择题中有且只有一个答案是正确的这一特点,结合估算、特例、逻辑分析等手段先排除一些肯定是错误的选项,从而缩小选择范围.
例2 直线ax-y+b=0与圆x2+y2-2ax+2by=0的图形可能是( ).
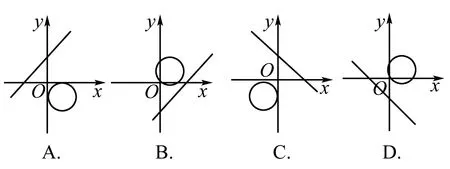
解析 由圆的方程知圆必过原点,所以排除A、C选项,圆心(a,-b),由B、D两图知a>0,-b>0.直线方程可化为y=ax+b,可知应选B.
三、特例法
用符合条件的特例来检验各选项,排除错误的,留下正确的一种方法叫特例法.常用的特例有特殊数值、特殊函数、特殊方程、特殊数列、特殊图形、特殊角、特殊位置等.用特例法解选择题时,一是特例选取得要合理,二是特例选取得越简单、越特殊越好.
A.a1+a101>0 B.a2+a102<0
C.a3+a99=0 D.a51=51
解析 取满足题意的特殊数列an=0,则a3+a99=0,故选C.
四、估算法
估算法是利用某些特殊的数、点、式、图或缩小考查的范围去确定答案的方法.此法可避免繁杂的推理和运算,避免“小题大做”.
例4 已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是( )

五、割补法
“能割善补”是解决几何问题常用的方法,巧妙地利用割补法,可以将不规则的图形转化为规则的图形,这样可以使问题得到简化,从而缩短解题时间.
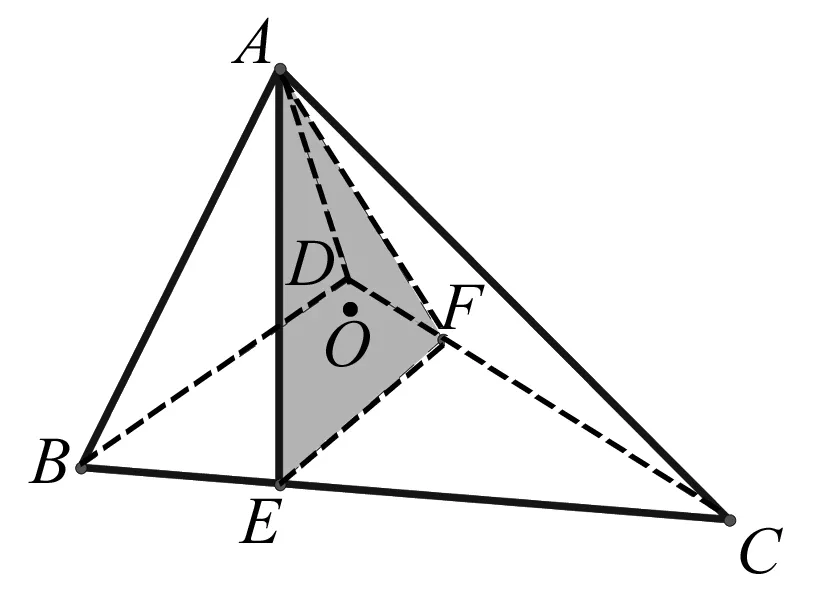
例5 如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( ).
A.S1S2B.S1S2
C.S1=S2D.S1,S2的大小关系不能确定

六、极限法
从有限到无限,从近似到精确,从量变到质变,应用极限法解决某些问题,可以避开抽象、复杂的运算,降低难度,优化解题过程.
A.sin(sinθ) B.sin(sinθ)>cosθ>cos(cosθ) C.sin(cosθ) D.sin(cosθ) 就是对有关概念进行全面、正确、深刻的理解或对有关信息提取、分析和加工后而作出判断和选择的方法. 例7 若△ABC的三边a、b、c满足等式acosA+bcosB=ccosC,则此三角形必是( ). A.以a为斜边的直角三角形 B.以b为斜边的直角三角形 C.等边三角形 D.其他三角形 根据题设条件作出所研究问题的曲线、有关图形或草图,借助几何图形的直观性、形状、位置、性质等图形特征作出正确的判断,得出结论. 例8 若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=|x|,则函数y=f(x)(x∈R)的图象与函数y=log3|x|的图象的交点个数为( ). A.2 B.3 C.4 D.无数个 解析 由已知条件可作出函数f(x)及y=log3|x|的图象,如右图.由图象可得其交点的个数为4个,故应选C. 从考试的角度来看,解选择题只要选对就行,至于用什么“策略”,“手段”都是无关紧要的,所以人称可以“不择手段”.高考中选择题的解答以提高速度,节省时间为原则,因此需要平时不断积累,养成巧解、速解的解题习惯. G632 B 1008-0333(2017)10-0006-02
七、分析法
八、数形结合法

