内爆炸作用下公轨合建盾构法隧道非封闭式内衬结构动力响应及抗爆性能分析

2017-05-17肖明清何应道

振动与冲击 2017年9期

关键词：抗爆行车道塑性

张景，封坤，何川，肖明清，王维，何应道

(1. 西南交通大学交通隧道工程教育部重点实验室，成都 610031；2. 中铁第四勘察设计院集团有限公司，武汉 430063)

内爆炸作用下公轨合建盾构法隧道非封闭式内衬结构动力响应及抗爆性能分析

张景1，封坤1，何川1，肖明清2，王维1，何应道2

(1. 西南交通大学交通隧道工程教育部重点实验室，成都 610031；2. 中铁第四勘察设计院集团有限公司，武汉 430063)

以武汉市三阳路公轨合建越江隧道为工程背景，采用数值仿真手段，对隧道行车层及轨行区不同位置、不同装药量、接触及非接触内爆炸作用下结构加速度、位移动力响应特征及结构塑性区分布、破坏形式进行研究。结果表明：内爆炸作用下，结构加速度及位移响应随爆炸发生迅速增大继而逐渐衰减，其中位移衰减速度较缓慢、衰减程度也较小，起爆点两侧2倍隧道直径范围内衬砌位移响应均较显著；装药量一定时，结构加速度响应的主要影响因素为距起爆点的距离，而结构刚度大小是影响位移响应的主要因素；结构塑性区易出现在起爆点附近、非封闭内衬结构的连接与转角处以及结构刚度较小的部位，其范围大小主要由炸弹装药量决定，管片结构未出现塑性区；结构的破坏形式主要为混凝土板表面爆坑、贯穿、撕裂破碎等。加厚行车道板或在其表面加设抗爆钢板均可显著减小结构塑性区、减轻破坏程度，相比之下加设钢板的措施更具可行性。

盾构法隧道；内爆炸；公轨合建断面；动力响应；抗爆性能

城市地铁、水下隧道等城市交通大动脉人员密度大、进出方便、发生灾难后疏散救援困难，容易成为恐怖分子袭击的公共基础设施。尤其对于水下盾构法隧道[1]，一旦发生较大规模爆炸破坏，隧道结构将难于修复，很可能危及整座隧道的安全，必须采用有效的措施防患于未然。随着大型越江盾构隧道的广泛兴建，盾构隧道的抗爆问题成为了隧道结构设计的新挑战。

近年来，伦敦、巴黎、莫斯科等世界著名城市的地铁系统均遭受过炸弹爆炸袭击，造成了大量人员伤亡、巨额财产损失以及深远的社会影响[2-3]。许多学者已经意识到隧道内爆炸对结构的危害性，并展开了一定程度的研究，主要集中在理论研究及数值模拟方面：杨科之等[4]针对内爆炸荷载的特点导出了用于计算结构等效静载的动效系数解析表达式；李献忠等[5]利用隧道内爆炸超压折线模型对双线地铁单侧内爆炸引起衬砌的动力响应特征进行动力分析；刘沐宇等[6]采用数值模拟手段对盾构隧道行车道板上接触爆炸进行模拟，探明了盾构隧道内接触爆炸作用下衬砌结构的动力响应规律；马险峰等[7]采用动力有限元方法计算并分析了不同装药量及不同爆炸方式下衬砌结构的动力响应和安全特性；田志敏等[8]采用三维有限元方法经计算得出衬砌的反射冲击波荷载峰值分布规律及估算衬砌上反射超压峰值的公式；邬玉斌等[9-10]采用数值模拟的手段研究了盾构隧道在内爆炸冲击荷载作用下的破坏机理，揭示了管片和螺栓的破坏特征。

相较普通交通隧道，公轨合建隧道发生内爆炸的风险显著增加，结构动力响应特殊，而现有研究多以中小直径地铁盾构隧道为例，对于断面形式复杂的大型公铁两用隧道发生内爆炸的影响研究未见述及。有鉴于此，本文以武汉三阳路公轨合建越江盾构隧道为依托，分析了隧道行车层及轨行区不同位置、不同装药量、不同爆炸方式作用下结构的动力响应特征、破坏特征及抗爆性能，同时针对行车层加设抗爆钢板以及加厚行车道板等措施的抗爆效果进行分析，以期为类似工程的抗防爆提供有益参考。

1 工程概况

武汉三阳路越江隧道为城市道路与轨道交通7号线共用过江通道，过江段采用公轨同管合建形式，建成后将成为世界上第一座公轨合建的盾构隧道。

隧道主体结构采用“管片衬砌+非封闭式内衬”的结构形式，分为上中下三层，上层为烟道板、中间层为三车道行车层、下层为武汉轨道交通7号线轨行区以及疏散通道和电缆廊道(见图1)，管片内径13.9 m、外径15.2 m，其断面直径位居国内第一，世界前三。

图1 三阳路隧道横断面图

隧道全长4 600 m，其中江中盾构段长2 590 m，主要在高透水性的粉细砂地层穿越，在江中段约1 100 m范围隧道切入基岩，基岩主要为强风化泥质粉砂岩、弱风化粉砂质泥岩以及弱胶结砾岩，天然抗压强度约1.2～6 MPa，隧道结构承受最大水压达0.65 MPa。三阳路隧道纵断面示意图见图2所示。

图2 三阳路隧道纵断面图

2 爆炸荷载模拟方法

受限于昂贵试验经费和试验条件，数值模拟成为爆炸效应模拟的有效手段，著名显示动力分析程序LS-DYNA特别适合爆炸、冲击等高度非线性的复杂力学过程，成为研究此类问题的首选，得到广泛应用[11]，该软件中特有的*LOAD_BLAST关键字将Conwep空气荷载计算程序编入DYNA计算程序，按照距离、入射角等条件计算荷载到达结构表面的时间、反射超压、冲量等空气荷载爆炸参数，同时还可以分别考虑接触与非接触爆炸等情况。使用该方法可以避免采用ALE算法求解流固耦合问题时的低效率问题，同时在计算精度上较直接将爆炸荷载简化成线性节点力的方法有较大的提高，成为研究结构在爆炸荷载作用下的动力响应问题的一种较理想的方法[12-13]。*LOAD_BLAST关键字中的爆炸荷载计算为

P(t)=Prefcos2θ+Pin(1+cos2θ-2cosθ)

(1)

Pref=Pr0(1-t/t0)e-at/t0

(2)

Pin=Ps0(1-t/t0)e-bt/t0

(3)

式中:θ为爆炸入射角；Pref为反射压力；Pin为入射压力；Ps0为入射超压峰值；Pr0为反射超压峰值；a为反射压力衰减系数；b为入射压力衰减系数；t0为正压作用时间。

3 数值模拟分析

3.1 计算模型

计算选取江心处断面，隧道所处地层从上到下依次为粉细砂层、弱胶结砾岩层和中胶结砾岩层，计算时为了消除边界效应的影响，一般要求隧道距离模型侧边界的距离大于隧道直径的3倍。本次计算模型纵向长度63 m，横向长度106.4 m，模型底部距离隧道底部45.2 m，满足计算要求，模型采用三维实体单元模拟，经试算可知，受非封闭式内衬的保护，管片衬砌受爆炸作用较小，结构动力响应研究重点为非封闭式内衬，本文为提高计算效率，采用盾构管片设计中常采用等效刚度连续介质模型，即引入刚度有效率(≤1)表征接头对整环刚度的削弱，本文取0.8[14]。为均衡计算精度及效率，采用渐变式网格划分，即越靠近起爆点处的隧道及地层模型采用细密的网格，相反则采用较稀疏的网格，模型总单元数710 880，衬砌结构网格划分如图3(a)所示，地层模型网格划分如图3(b)所示。

为了避免波在模型边界的反射对求解域的影响，在模型底部、左右侧边及后边界施加无反射边界(Non-reflect Boundary)来模拟地层的半无限性；模型顶部为地表；模型前表面为对称边界，设置沿隧道纵向的位移约束。

(a)隧道模型网格划分图(b)地层模型网格划分图

图3 计算模型网格划分图

Fig.3 Numerical simulation model

3.2 材料本构及计算参数

混凝土采用PLASTIC_KINEMATIC模型，该模型特有的失效功能在计算过程中程序自动判定单元是否失效并将失效单元删除，可有效地模拟衬砌结构在爆炸荷载作用下的弹塑性及失效等力学行为，该模型使用考虑应变率的Cowper-Symonds模型，其屈服应力表达式为

(4)

根据《混凝土结构设计规范(GB 50010—2010)》[15]并参考文献[6, 8]确定本次计算混凝土材料参数如表1所示。本文主要研究隧道结构的动力响应特征，采用DRUCKER_PRAGER模型模拟各地层，其材料参数见表2所示。

表1 混凝土材料参数

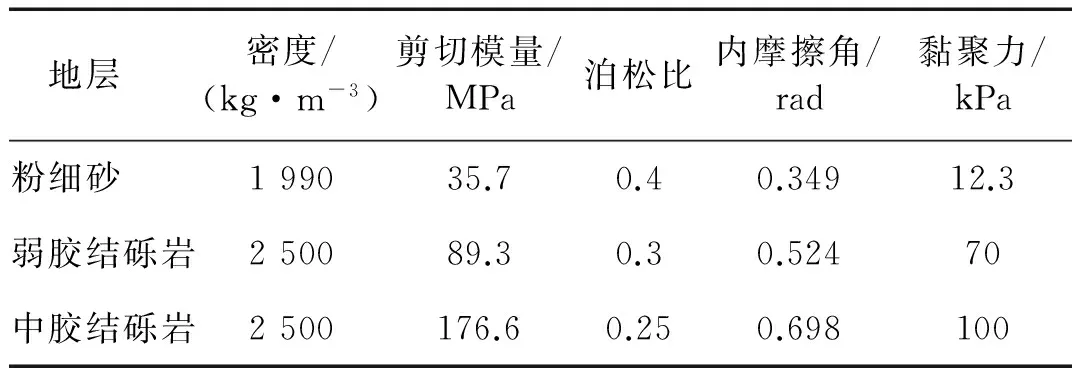
表2 地层材料参数

3.3 计算工况

公轨合建隧道各层使用功能不同，因此可能的炸弹种类、起爆点位置众多，分析中采用不同装药量的固体TNT炸药来区分不同炸弹种类，装药量参考美国联邦应急管理局给出的评估数据(见表3)，行车层主要考虑可能进入小轿车炸弹(230 kg TNT)和小卡车炸弹(2 000 kg TNT)导致爆炸；轨行区内只能人员进入，且有较严格的安保措施，可能的炸弹种类为人体炸弹(2 kg)和箱包炸弹(5 kg)及隐蔽炸弹(40 kg)，据文献[6]可知装药量较小时，隧道内爆炸对衬砌结构影响较小，为简化计算工况，轨行区内仅考虑隐蔽炸弹(40 kg TNT)影响。中间行车道板(即轨行区上方行车道板)的破坏将直接危及行车层与轨行区的安全，该处为抗爆设防的关键部位。本文以工况B1为对照，分别采取加设抗爆钢板、加厚行车道板的抗爆措施，分析其抗爆效果。各工况计算时间均取200 ms，具体工况见图4、表4所示。

4 计算结果分析

4.1 隧道结构加速度响应

沿隧道纵向在距起爆点断面0D、0.5D、1.0D、2.0D(D为隧道直径)距离上选取四个监测断面(图5(c))，各断面内沿行车层或轨行区洞周设置不同监测点(见图5(a)和图5(b))以监测爆炸过程中结构的动力响应。工况A1-1及A4分别为行车层和轨行区内爆炸工况，爆炸过程中衬砌单元没有失效破坏，以上述两工况为例能够完整反映结构动力响应特征。

表3 炸弹种类与TNT装药量对照表

图4 不同起爆点位置示意图

表4 计算工况对照表

Tab.4 Calculation cases table

爆炸类型工况位置装药量/kg备注非接触A1-1A140A1-2A1230A1-3A12000A2A22000A3A3230A4A440接触B1B1230B2B2230B3B340B4B440C1B12302cm厚Q235钢板C2B12302cm厚Q345钢板C3B1230行车道板厚70cmC4B1230行车道板厚100cm注:1.计算时Q235钢板极限强度取375MPa;Q345钢板极限强度取470MPa[16];2.原行车道板厚度(未采取抗爆措施时)为50cm

(a)行车层(b)轨行区

经计算可知，相同断面内各测点加速度响应特征类似，图6和图7中以测点1加速度时程曲线为例进行说明。据图可知衬砌结构加速度在爆炸发生瞬间急剧增大并迅速衰减，剧烈的振动加速度仅持续约20 ms便迅速衰减至较低水平，且随着距起爆点所在断面距离的增加，不同断面相同位置测点加速度峰值出现的时间稍向后推移，在时程曲线呈现出“错峰”的现象，表明爆炸冲击波沿隧道纵向的传播效应。

图6 A1-1工况各断面测点1加速度时程曲线

图7 A4工况各断面测点1加速度时程曲线

对比图6和图7可知，相同装药量作用下，行车层测点1加速度峰值为993.04 m/s2，轨行区测点加速度峰值达到2 795.68 m/s2，约为行车层的2.8倍，这种现象可能是由于行车层具有较大的净空面积使得作用于结构上的反射冲击波荷载较小造成的；同时可以看出由于周围地层的较强约束作用，轨行区测点加速度值衰减速度明显快于行车层。值得注意的是，各测点具有三个方向加速度及位移，为方便比较及篇幅受限，文中测点加速度、位移为测点各方向加速度、位移合成值。

图8所示为工况A1-1、A4中各断面监测点加速度峰值衰减曲线，因所选工况结构对称、荷载对称，故只需分析一半测点。从图中可以看出随着测点远离起爆点所在断面，加速度峰值迅速减小，两图中断面4衬砌加速度均已减小至相当低的水平，爆炸荷载作用下，衬砌结构加速度响应显著区域为起爆点两侧2倍隧道直径范围内。如图8(a)所示，行车道板上方1 m非接触爆炸时，测点加速度峰值大小依次为行车道板中部(测点4)、行车道板侧墙墙脚(测点3)、烟道板牛腿连接处(测点2)、烟道板跨中(测点1)；据图8(b)可知，轨道板上方2.5 m非接触爆炸时，测点加速度大小依次为轨行区侧墙中部(测点2)、轨道板中部(测点3)、行车道板跨中(测点1)。综上可知，非接触爆炸时，距起爆点越近的衬砌加速度峰值越大，反之越小。

(a)工况A1-1(b)工况A4

图8 工况A1-1、A4各断面加速度峰值衰减曲线

Fig.8 Attenuation curve of peak acceleration in case A1-1 and case A4

4.2 隧道结构位移响应

图9和图10所示为各断面测点1位移时程曲线，从图9可看出行车层爆炸时，各测点位移时程曲线为较规则的正弦波形，断面1测点位移在第一个振荡周期即达到最大值随后呈振荡衰减的趋势，与加速度的衰减速度相比，位移的衰减速度较缓慢，位移峰值衰减程度也较小；断面2、断面3、断面4内位移峰值并未出现在首次震荡中，而是随着爆炸冲击波的传播逐渐达到峰值，而后逐渐衰减，与加速度表现出的特征相似，位移时程曲线仍能反映出爆炸冲击波沿隧道纵向的传播效应。

图9 A1-1工况各断面测点1位移时程曲线

图10 A4工况各断面测点1位移时程曲线

据图10可知，轨行区内爆炸时，位移时程曲线也呈现出类似正弦的波形，但比起行车层波形很不规则，测点位移经几次震荡后达到峰值，较高水平的振荡位移持续约50 ms后逐渐降低，与行车层测点位移时程曲线相比，轨行区测点位移时程曲线具有较高的振动频率。

图11所示为工况A1-1、A4中各断面监测点位移峰值衰减曲线。从图中可以看出随着测点远离起爆点所在断面，位移峰值逐渐减小，与加速度峰值衰减程度相比，位移衰减程度较低，以两图中位移最大测点为例，断面4测点位移峰值约为断面1的1/5，与加速度响应相比，衬砌位移响应显著区域的范围较大。

(a)工况A1-1(b)工况A4

图11 工况A1-1、A4各断面位移峰值衰减曲线

Fig.11 Attenuation curve of peak displacement in case A1-1 and case A4

据图11可知，行车道板上方1 m非接触爆炸时，测点位移峰值大小依次为烟道板跨中部位(测点1)、行车道板跨中部位(测点4)、烟道板牛腿连接处(测点2)、行车道板侧墙墙脚(测点3)；轨道板上方2.5 m非接触爆炸时，测点位移峰值大小依次为轨行区侧墙中部(测点2)、行车道板跨中(测点1)、轨道板中部(测点3)。综上可知，一定装药量非接触爆炸时，影响衬砌位移响应的重要因素是结构的刚度值，结构刚度越小，位移响应越大。

4.3 结构塑性区分布及破坏形式

不同工况结构塑性区分布及破坏形式如图12、图13所示，其中图12为非接触爆炸工况，图13为接触爆炸工况。

据图12可知，非接触爆炸工况中，结构塑性区及失效破坏单元均出现在非封闭内衬上，管片结构未见塑性区。40 kg TNT在行车道板上方1 m处爆炸时(工况A1-1)，仅起爆点下方行车道板上形成半径35 cm半球形塑性区；230 kg TNT在相同位置爆炸时(工况A1-2)，起爆点下方行车道板上形成半径1 m的塑性区，其中部分单元失效破坏，塑性区中央出现半径70 cm、深20 cm的爆坑，同时烟道板跨中及牛腿连接处出现沿隧道纵向分布的塑性区，纵向长度约8 m(单侧，下同)；2 000 kg TNT在相同位置爆炸(工况A1-3)对行车层造成毁灭性的破坏，起爆点下方行车道板上半径1.5 m区域被爆炸冲击波贯穿，行车道板与轨行区侧墙连接处、行车层侧墙墙脚处均出现塑性区，而烟道板的破坏最为严重，塑性区纵向长度达到18 m，其中8 m范围内的烟道板被严重撕裂、破碎。行车道板上方2 m处2 000 kg TNT爆炸时(工况A1-4)结构的破坏形式与工况A1-3相似，其中行车道板上形成的塑性区及贯穿范围长度达到10 m；230 kg TNT在行车层右侧车道上方1 m爆炸时(工况A3)，破坏形式与工况A1-2类似，起爆点下方出现半径1 m的塑性区，同时出现半径60 cm、深20 cm的爆坑，烟道板跨中、牛腿连接处侧墙墙脚处出现塑性区；轨行区内40 kg TNT非接触爆炸(工况A4)对衬砌结构影响较小，仅在墙脚处出现有限的塑性区。

(a) 工况A1-1

(b) 工况A1-2

(e) 工况A3

(f) 工况A4

据图13可知，与非接触爆炸工况相同，结构塑性区及破坏失效单元均出现在非封闭内衬上，管片结构未见塑性区。230 kg TNT在行车道板跨中接触爆炸时(工况B1)，起爆点附近形成半径2.5 m塑性区，塑性区内行车道板被贯穿、掉块；行车层侧墙墙脚处230 kg TNT接触爆炸时(工况B2)，起爆点所在位置出现塑性区，部分单元失效破坏，但未能贯穿行车道板，此外烟道板牛腿连接处以及1/3跨度位置出现塑性区；轨道板顶部40 kg TNT接触爆炸时(工况B3)，塑性区仅出现在轨行区侧墙与行车道板连接部位，总体影响较小；轨行区侧墙中部40 kg TNT接触爆炸时(工况B4)，起爆点位置出现半径2.5 m的塑性区，并且在在塑性区内出现50 cm贯穿区域，侧墙墙脚及侧墙与行车道板连接处也出现塑性区。

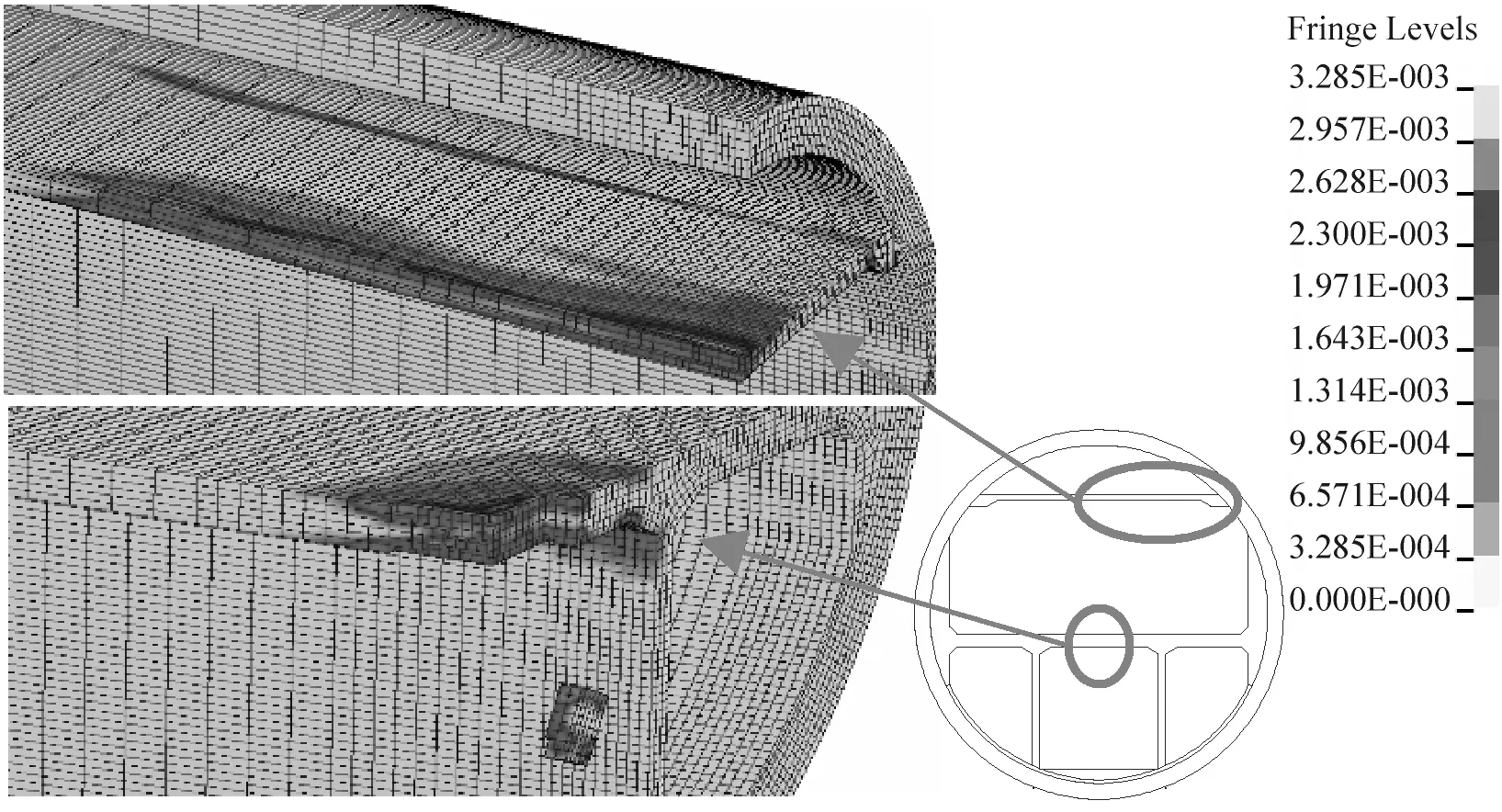
(a) 工况B1

(b) 工况B2

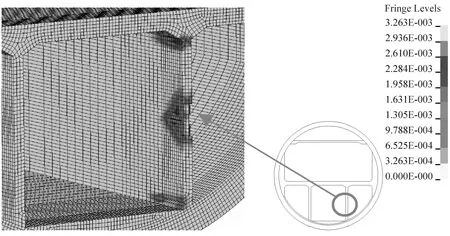
(d) 工况B4

4.4 不同抗爆措施抗爆效果

图14、图15为分别采取行车道板加设抗爆钢板和加厚行车道板的抗爆措施时行车道板塑性区分布及其破坏形式图。

(b) 加设2 cm Q345钢板

由图14可知，由于钢板屈服强度及极限强度均远高于混凝土，行车道板表面加设2 cm厚Q235、Q345抗爆钢板时，相同装药量爆炸作用下，起爆点附近行车道板混凝土上塑性区由2.5 m减小至1 m，爆坑深度约30 cm，未见行车道板贯穿，抗爆效果显著，其中采用Q345钢板时起爆点附近钢板上塑性区及撕裂区域半径达到0.5 m，约为采用Q235钢板时的一半。

(a) 70 cm行车道板

(b) 100 cm行车道板

由图15可知，由于加厚行车道板所致结构刚度增大，相同装药量爆炸作用下，起爆点附近行车道板顶、底部均出现半径1 m的塑性区；当行车道板厚度为70 cm时，其顶、底部均有混凝土单元破坏失效，但其并未被贯穿，影响深度约50 cm；当行车道板厚度为100 cm时，仅在行车道板顶部出现深度约50 cm的爆坑，顶、底部塑性区未连通。加厚行车道板的措施将不可避免地侵占隧道净空，可能导致建筑限界难于满足，同时因加厚行车道板所导致的结构自重增加迫使设计中必须对结构受力进行重新验算。

5 结论

经上文计算分析，可以得出以下结论及建议：

(1) 采用“管片衬砌+非封闭式内衬”形式的公轨合建盾构隧道结构加速度响应在爆炸发生瞬间急剧增大并迅速衰减，轨行区相比行车层加速度峰值更高、衰减速度更快；爆炸荷载作用下，衬砌加速度受影响显著区域分布在起爆点两侧2倍隧道直径范围内；装药量一定时，影响结构加速度响应的主要因素为距起爆点的距离，距离越近，加速度响应越剧烈。

(2) 隧道结构位移响应在爆炸发生时迅速增大并逐渐衰减，位移时程曲线的波形为接近正弦的振荡曲线，与加速度相比，位移衰减速度较缓慢且衰减程度也较小；装药量一定时，影响结构位移响应的主要因素为结构刚度的大小，结构刚度越小，位移响应越明显。

(3) 此类隧道结构在内爆炸作用下塑性区仅出现在非封闭内衬上，管片结构未出现塑性区；塑性区范围大小主要由炸弹装药量决定；装药量一定时，接触爆炸所致结构塑性区比非接触爆炸时更大，破坏更严重。内爆炸可能造成结构失效破坏，主要表现为：行车道板上出现圆锥体爆坑，行车道板及轨行区侧墙的贯穿、掉块，烟道板的撕裂、破碎等。

(4) 结构易出现塑性区的位置主要为：① 非接触爆炸时为距离起爆点较近位置，接触爆炸时为起爆点所在处附近；② 结构形式较复杂的连接、转角部位，如烟道板牛腿连接处、侧墙墙脚以及行车道板和侧墙连接处；③ 结构刚度较小的部位，如烟道板跨中处。

(5) 对行车道板采用加设抗爆钢板和加厚两种抗爆措施可显著减小行车道板塑性区面积、减轻行车道板破坏程度，并能有效防止小轿车接触爆炸导致的行车道板贯穿破坏。加设抗爆钢板相比加厚行车道板的措施对结构自重及受力影响较小，是一种提高结构抗爆性能的有效措施。

[1] 何川，封坤，方勇. 盾构法修建地铁隧道的技术现状与展望[J]. 西南交通大学学报，2015，50(1)：97-109.

HE Chuan, FENG Kun, FANG Yong. Review and prospects on constructing technologies of metro tunnels using shield tunneling method[J]. Journal of Southwest Jiaotong University, 2015, 50(1):97-109.

[2] 邬玉斌.地下结构偶然性内爆炸效应研究[D]. 哈尔滨：中国地震局工程力学研究所，2011.

[3] 刘晶波，闫秋实，杜义欣，等.地铁地下结构内爆炸防护问题研究[J]. 振动与冲击，2008，27(8)：16-19.

LIU Jingbo, YAN Qiushi, DU Yixin, et al. Study on the protection of subway structures subjected to blast[J]. Journal of Vibration and Shock, 2008, 27(8): 16-19.

[4] 杨科之，杨秀敏，王年桥.内爆荷载作用下结构等效静载计算方法[J]. 解放军理工大学学报(自然科学版)，2002，3(4)：31-33.

YANG Kezhi, YANG Xiumin, WANG Nianqiao. Equivalent static load calculation method of structures subjected to internal explosion[J]. Journal of PLA University of Science and Technology(Natural Science), 2002, 3(4):31-33.

[5] 李忠献，刘杨，田力.单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应与抗爆分析[J]. 北京工业大学学报，2006，32(2)：173-181.

LI Zhongxian, LIU Yang, TIAN Li. Dynamic response and blast-resistance analysis of double track subway tunnel subjected to blast loading within one side of tunnel[J]. Journal of Beijing University of Technology, 2006,32(2): 173-181.

[6] 刘沐宇，卢志芳. 接触爆炸荷载下长江隧道的动力响应分析[J]. 武汉理工大学学报，2007，29(1)：113-117.

LIU Muyu, LU Zhifang. Analysis of dynamic response of Yangtze river tunnel subjected to contact explosion loading[J]. Journal of Wuhan University of Technology, 2007,29(1): 113-117.

[7] 马险峰，隋涛，尚金华,等. 双圆盾构隧道在内部爆炸荷载下的响应分析[J]. 同济大学学报(自然科学版)，2011，39(7)：983-988.

MA Xianfeng, SUI Tao, SHANG Jinhua, et al. Response analysis of dot shield tunnels under internal explosion[J]. Journal of Tongji University (Natural Science), 2011, 39(7):983-988.

[8] 田志敏，邬玉斌，罗奇峰. 隧道内爆炸冲击波传播特性及爆炸荷载分布规律研究[J]. 振动与冲击，2011，30(1)：21-26.

TIAN Zhimin, WU Yubin, LUO Qifeng. Characteristics of in-tunnel explosion-induced air shock wave and distribution law of reflected shock wave load[J]. Journal of Vibration and Shock, 2011，30(1): 21-26.

[9] 邬玉斌，刘如山，田志敏.盾构隧道管片接头在内爆炸作用下的动力反应[J]. 武汉理工大学学报，2011，33(7)：107-111.

WU Yubin, LIU Rushan, TIAN Zhimin. Analysis on dynamic response of a shield tunnel under internal explosion loading[J]. Journal of Wuhan University of Technology, 2011, 33(7): 107-111.

[10] 邬玉斌，田志敏，罗奇峰.偶然性内爆炸作用下盾构隧道的破坏特性分析[J]. 岩石力学与工程学报，2011，30(增刊2)：3434-3442.

WU Yubin, TIAN Zhimin, LUO Qifeng. Analysis on failure characteristics of shield tunnel under accidentally internal explosion loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup 2): 3434-3442.

[11] 石党勇，李裕春，张胜民. 基于ANSYS/LS-DYNA8.1进行显式动力分析[M]. 北京：清华大学出版社，2005.

[12] LSTC. LS-DYNA keyword user’s manual (Version 971)[M]. California: Livermore Software Technology Corporation, 2007.

[13] LSTC. LS-DYNA theory manual[M]. California: Livermore Software Technology Corporation, 2014.

[14] 土木学会日. 隧道标准规范(盾构篇)及解说[M]. 朱伟,译. 北京：中国建筑工业出版社，2011.

[15] 混凝土结构设计规范：GB 50010—2010[S]. 北京：中国建筑工业出版社，2010.

[16] 钢结构设计规范：GB 50017—2003[S]. 北京：中国建筑工业出版社，2003.

Dynamic response and anti-explosion behavior analysis for combined railway and roadway shield tunnel’s unclosed inner lining structure under internal explosion

ZHANG Jing1， FENG Kun1， HE Chuan1， XIAO Mingqing2， WANG Wei1， HE Yingdao2

(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan 430063, China)

Taking the Sanyang Road-cum-Urban Rail tunnel as the engineering background, the numerical simulation method was employed to analyze dynamic responses of acceleration and displacement of the tunnel structure, the distribution of the structural plastic region, and destruction forms under the internal explosion action with different kinds of explosive charge located in different positions. The results showed that the dynamic responses of acceleration and displacement of the structure increase rapidly and then decay gradually along with the explosion; the explosion has a deeper influence on displacements, its single side influence range is larger than 2 times of the tunnel diameter; under a certain explosive charge acceleration responses are mainly influenced by the distance to the initiation explosion point, and the stiffness of the structure is the main influence factor of displacement responses; the plastic region of the structure is dependent on explosive charge, it appears near the initiation explosion point, corners and low-stiffness components of the inner liner and does not appear in the segmental liner under the action of internal explosion; the destruction forms of the structure are mainly divided into blasting craters of surface, and penetration or tearing of concrete slabs; thickened roadway slabs or their additional anti-explosion steel plates reduce plastic regions more significantly.

shield tunnel；internal explosion；combined railway and roadway cross-section；dynamic response；anti-explosion behavior

国家自然科学基金(U1134208；U1361210；51578462)；中央高校基本科研业务费专项资金资助(2682015CX077)

2015-10-28 修改稿收到日期：2016-03-21

张景男，博士生，1988年生

封坤男，博士，讲师，1983年生

U451.4

10.13465/j.cnki.jvs.2017.09.034