G104国道绍兴段公路桥梁疲劳车辆荷载模型研究

赵建峰

(浙江交通职业技术学院，杭州 311112)

G104国道绍兴段公路桥梁疲劳车辆荷载模型研究

赵建峰

(浙江交通职业技术学院，杭州 311112)

基于WIM系统采集得到G104国道绍兴段一个月的交通荷载数据，首先划分交通荷载的车型类别，并对轴载质量、轴距等参数进行统计分析。然后，根据疲劳等效损伤原理，建立疲劳等效车辆模型。在此基础上，推导得出适用于该路段的疲劳荷载谱，并选用20m钢筋混凝土简支T梁构建疲劳验算模型，基于应力-寿命曲线和Miner线性累积损伤理论计算分析各疲劳车型产生的疲劳损伤度值。最后，根据各疲劳车型的疲劳损伤度比大小，选取典型疲劳代表车型，建立适用于G104国道绍兴段的公路桥梁疲劳车辆荷载模型。通过计算分析可知：G104国道绍兴段的N7疲劳车型产生的疲劳损伤值最大，钢筋应力幅值及实际加载循环次数是决定疲劳损伤值大小的主要参数。钢筋应力幅值主要由疲劳荷载的车型与载重质量大小控制，而实际加载循环次数则与通行荷载的交通流量大小密切相关。

公路桥梁；疲劳荷载；S-N曲线；Miner准则

0 引 言

疲劳是指材料在应力或应变的反复作用下所产生的性能变化。材料承受荷载的反复作用时，即使所产生的最大应力低于极限强度(甚至还低于屈服强度)时仍会出现破坏，这种破坏就称为疲劳破坏。桥梁在运营期内承受着车辆荷载的反复作用，结构疲劳损伤不断积累，疲劳破坏已成为桥梁结构破坏的主要原因之一。疲劳车辆荷载模型是研究疲劳破坏问题的基础，最新修订的《公路桥涵设计通用规范》(JTG D60-2015)[1]中新增加了Ⅰ、Ⅱ、Ⅲ型三种疲劳荷载计算模型，分别采用等效的车道荷载、双车模型和单车模型进行结构疲劳验算。现行规范中制定的疲劳设计荷载标准为桥梁结构的抗疲劳设计和疲劳强度验算提供了计算依据。然而，我国地域辽阔，区域经济发展存在差异，各地区车辆荷载的运行规律和分布特点有着明显不同，采用全国统一的疲劳车辆荷载模型尚无法满足疲劳验算的精细化计算要求。为研究典型路段的疲劳荷载谱，选择G104国道绍兴段作为监测路段，基于动态称重系统结合交通荷载调查分析，建立能够代表当地交通荷载实际运营状况的疲劳车辆荷载模型，从而填补了该路段实际通行交通荷载调查数据的空白，为该地区今后的公路桥梁疲劳设计验算提供参考依据。

1 交通荷载调查与车型分类

为了采集到准确可靠的交通车辆荷载数据信息，选择G104国道绍兴段钟家湾立交桥主桥一联三跨(22+38+22)m预应力混凝土连续梁桥作为监测桥梁(如图1所示)，基于动态称重(WIM，Weigh-In-Motion)系统采集实际通过桥梁的车辆荷载数据。该观测点的特点是交通量较大，运营车辆以中小型客货车为主，车型种类众多，重车及特重车辆在夜间行驶的比例较大，该调查路段的交通状况可作为绍兴地区一般公路的典型代表。

钟家湾立交桥车道布置为单向双车道，在引桥第10跨安装弯板式传感器，单个车道各埋设2块弯板，弯板埋设位置如图2所示。WIM系统可以连续记录完整的交通荷载信息数据，包括车辆类型、轴距和轴载质量等参数。

基于WIM系统结合交通荷载实地调查，参考国家统一规定的车辆类型划分标准，确定G104国道绍兴段的交通荷载调查车型分类，具体车型划分类别及参数详见文献[2]。

图1 G104国道绍兴段钟家湾立交桥地理位置图

图2 弯板式动态称重设备埋设位置示意图

2 公路桥梁疲劳荷载谱推导

2.1 等效疲劳荷载模型建立

基于WIM系统采集得到G104国道绍兴段一个月的实测交通荷载数据，首先按照加权平均计算方法，由式(1)求出单个车型各个轴之间的等效轴距。然后，依据等效疲劳损伤原理[3]，由式(2)计算推求单个车型各个轴的等效轴载质量。

Dei=∑(fpDpi)

(1)

Wej=[∑(fpWpj3)]1/3

(2)

式中：fp表示单个车型中第p辆车的相对频率；Dpi表示第p辆车的第i个轴距；Dei表示单个车型中第i个轴距的等效轴距；Wpj表示单个车型中第p辆车的第j个轴的轴载质量；Wej表示单个车型中车辆第j个轴的等效轴载质量。

根据上述方法，可分别计算得到各疲劳等效荷载模型的等效轴距和等效轴载质量，如表1所示。

2.2 公路桥梁疲劳荷载谱推导

由表1计算结果可知，V1疲劳等效车型的总质量均小于2t，并且部分疲劳等效车型在总交通流量中所占的比例甚小，在实际中对桥梁造成的疲劳损伤基本可以忽略不计。为了简化疲劳荷载谱所包含的车型种类，疲劳荷载谱的推导遵循以下原则：

1)将车辆等效总质量M<3t的车型忽略不计；

2)将所占比例≤ 0.1%的车型忽略不计；

3)考虑到两轴车的数量较大，但车辆总质量相对较小，可合并形成统一的疲劳荷载模型。

根据以上原则，将V1、V6、V13、V14等车型参数剔除后，最终得到G104国道绍兴段的疲劳荷载谱如表2所示。

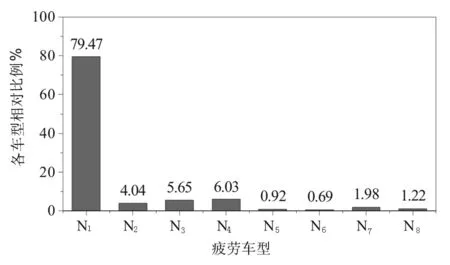
图3 104国道绍兴段各疲劳车型相对比例分布图

车辆类型等效轴距(m)等效轴载质量(t)AD1AD2AD3AD4AD5AW1AW2AW3AW4AW5AW6总质量(t)占比(%)V12.59////0.810.74////1.5573.64V23.87////2.676.01////8.684.53V33.20////1.702.97////4.677.32V45.37////4.348.48////12.824.20V54.76////3.778.96////12.734.78V66.171.30///5.098.024.43///17.540.10V71.774.91///4.134.2812.68///21.091.06V83.451.29///5.6610.9610.62///27.241.54V91.784.301.29//4.865.019.0210.61//29.501.49V113.737.181.32//3.676.955.435.52//21.570.27V123.456.511.281.31/4.439.186.496.027.08/33.200.21V131.742.555.651.29/3.092.274.753.663.02/16.790.02V143.081.325.041.32/4.286.756.537.098.86/33.510.01V153.091.286.871.311.295.6912.8812.913.7714.0315.2374.500.49V161.692.386.761.291.303.723.7811.178.537.848.4643.500.34

注：ADi表示车辆荷载第i个轴距；AWj表示车辆荷载第j根轴的轴载质量。

表2 G104国道绍兴段公路桥梁疲劳荷载谱

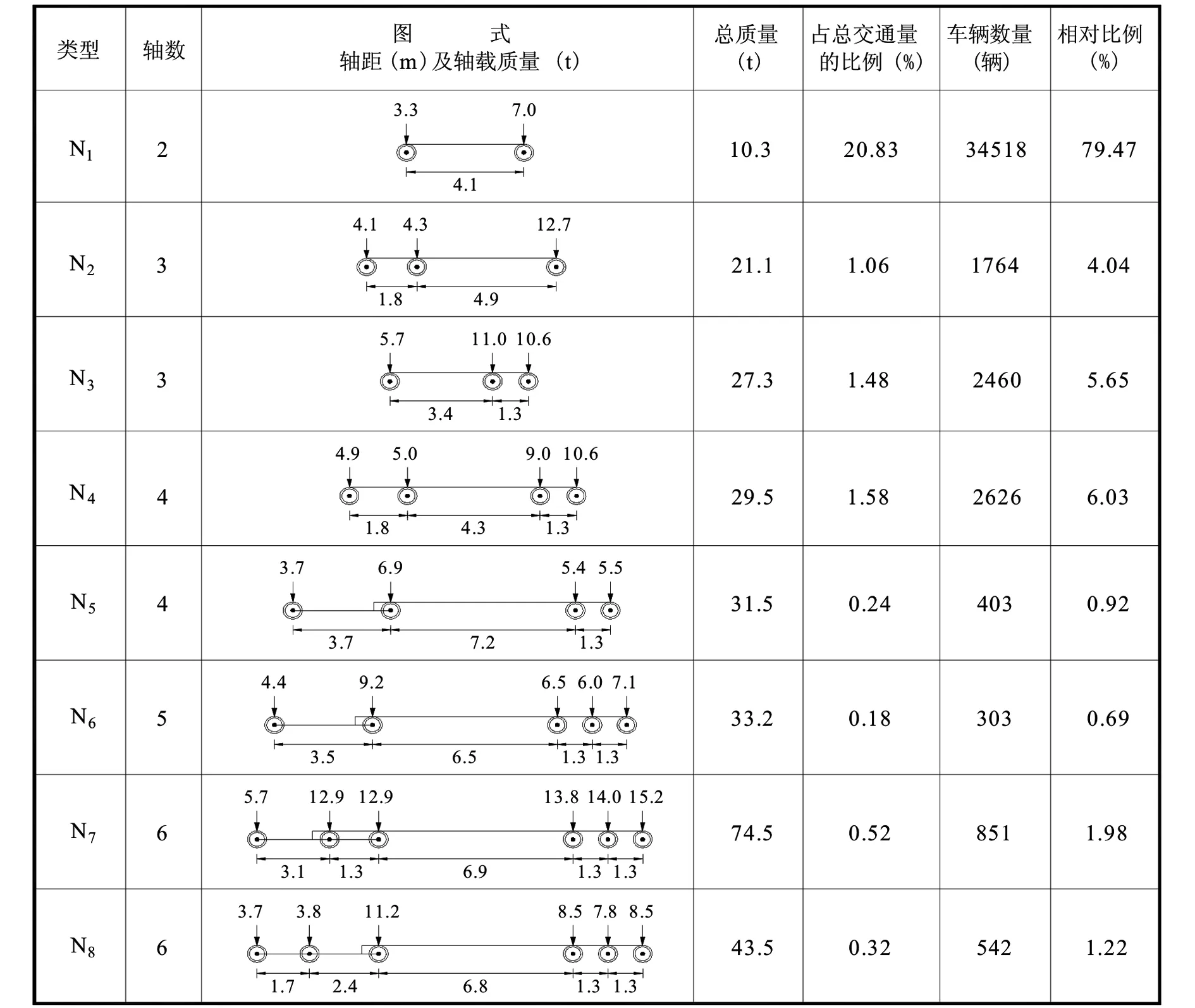
推导得到的G104国道绍兴段的疲劳荷载谱共包含8种车型，统一编号为N1～N8。从图3可以看出，疲劳车型N1占总交通量的相对比例最大，但该车型的车辆总重在所有疲劳车型中为最小。疲劳车型N5～N8属于拖挂车类型，占总交通量的相对比例为最小，但各疲劳车型的总质量均比其它车型大，其中，疲劳车型N7是所有疲劳车型中装载质量最大的车型，总质量为74.5t。

3 建立疲劳车辆荷载模型

选用计算跨径L=19.5m的钢筋砼简支T梁构建疲劳验算模型，T梁的主要尺寸如图4，所采用的材料特性取值及主要参数计算值如表3、表4。采用各疲劳车型对简支T梁进行加载，计算主梁结构的疲劳损伤值，并根据疲劳损伤值的大小，选取典型疲劳代表车型，建立适用于G104国道绍兴段的疲劳车辆荷载模型。结构疲劳损伤值的计算方法如下：

表3 20m钢筋混凝土简支T梁材料特性取值

表4 20m钢筋混凝土简支T梁主要参数计算表

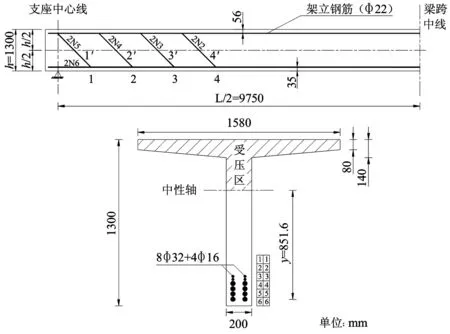
图4 20m钢筋混凝土简支T梁纵断面和跨中断面

(1)根据结构力学中的影响线加载法求解内力的计算原理，首先绘制出T梁跨中断面最大正弯矩影响线，采用各疲劳车型N1～N8对主梁结构按照影响线进行加载计算，求解得到跨中断面的最大正弯矩-时程曲线。以N1疲劳车为例进行计算分析，图5给出了N1疲劳车作用下跨中最大正弯矩-时程曲线图。

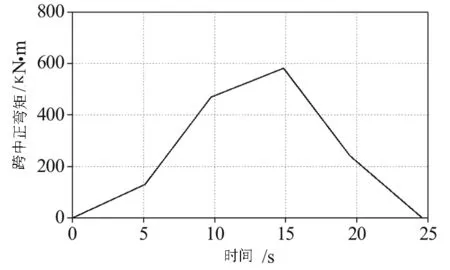
图5 N1疲劳车作用下跨中最大正弯矩-时程曲线

根据式(3)求解得到受拉区混凝土在N1疲劳车作用下的最大正应力-时程曲线(如图6)。

(3)

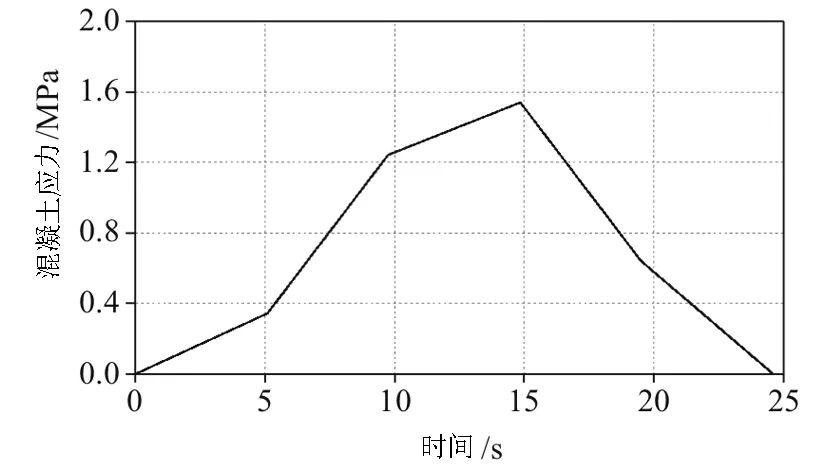
图6 N1疲劳车作用下混凝土最大正应力-时程曲线

在疲劳荷载作用下，结构一般处于弹性工作阶段，混凝土与纵向主筋的平均应变沿截面高度范围内呈线性分布，位于截面同一高度位置处的钢筋与混凝土应变值相等，即εs=εc。

根据胡克定律，按照式(4)可求解得到最底层受拉主筋的最大应力-时程曲线(如图7)。

(4)

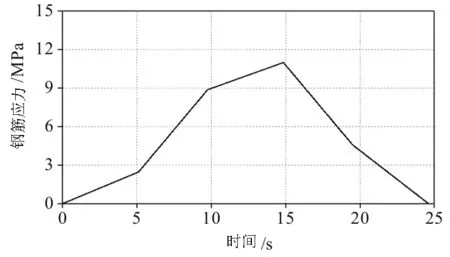
图7 N1疲劳车作用下主筋最大应力-时程曲线

(2)从钢筋的应力-时程曲线中提取出二维应力幅谱，如图8所示。然后，运用雨流计数法及 Goodman疲劳经验式(5)，求解得到受拉主筋的等效零均值应力幅值Sek[6]。

(5)

式中：Smk为受拉钢筋的应力均值；Sak为受拉钢筋的应力幅值；σb为受拉钢筋的屈服强度。

图8 钢筋应力-时程中提取的二维应力幅谱

图9 对接焊钢筋的疲劳抗力曲线

为了计算受拉主筋在不同应力水平下的疲劳寿命，本文采用铁科院推导得出的对接焊钢筋疲劳S-N曲线[5](如图9)，将Sek代入公式(6)可得到相应的疲劳寿命Nk。

(6)

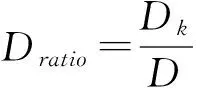
(7)

式中：nk为Sek应力水平下发生的循环次数，取设计基准期为100年的总交通量；MADTk为—月平均日交通流量。

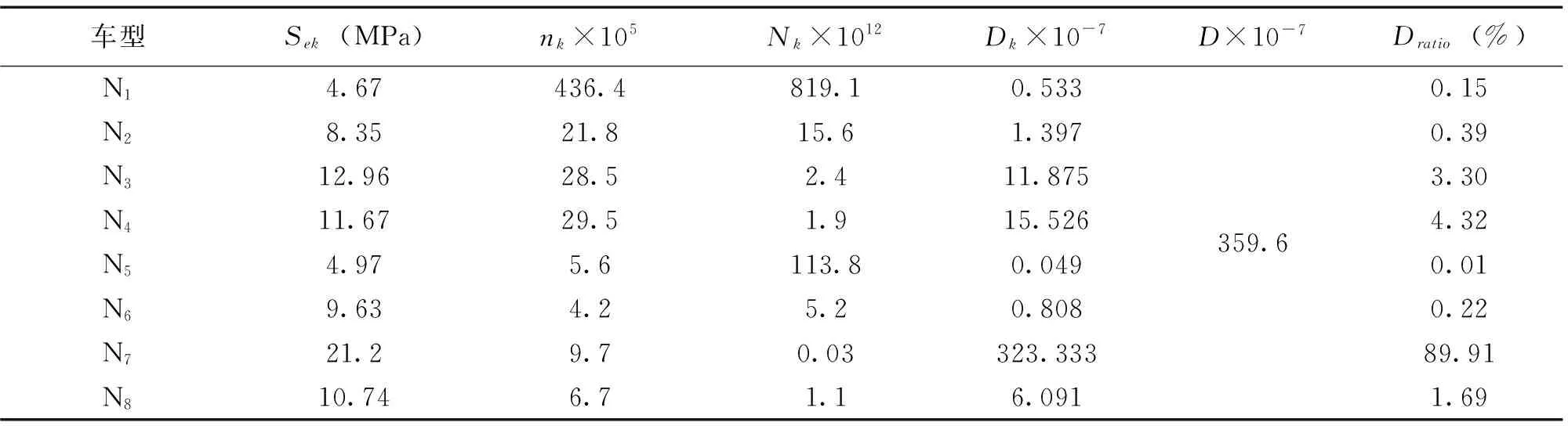
表5 104国道绍兴段各疲劳车型损伤度值计算

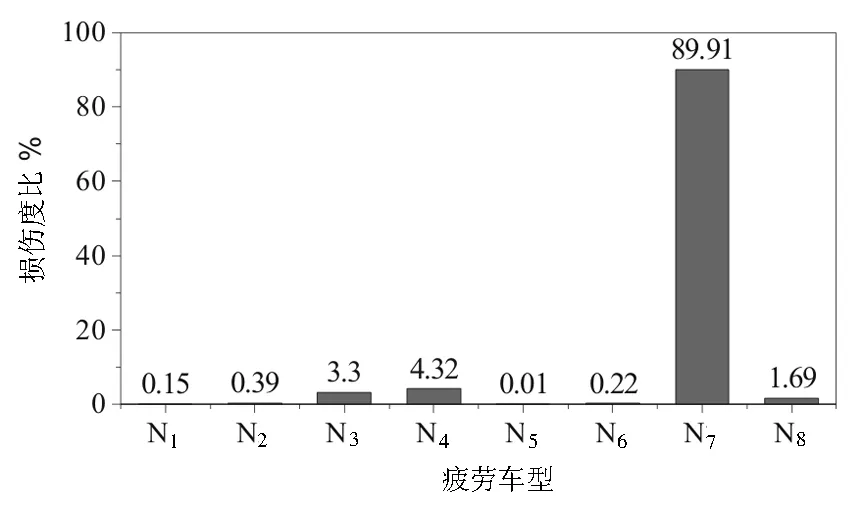
图10 104国道绍兴段各疲劳车型损伤度比计算值

由表5可知，钢筋应力幅值及实际加载循环次数是决定疲劳损伤值大小的主要参数。其中，钢筋应力幅值主要由疲劳荷载的车型及载重质量控制，而实际加载循环次数则与通行荷载的交通流量大小密切相关。从图10可以看出，N1、N2、N5、N6等疲劳车型对结构的疲劳损伤影响甚小，基本可以忽略不计。N3、N4、N8等疲劳车型会对结构的疲劳损伤产生一定的影响，但疲劳损伤值相对较小。通过对比分析可知，六轴疲劳车型N7的疲劳损伤度比最高，占总损伤的89.91%，说明该疲劳车型最易引起结构的疲劳损伤，是对结构疲劳损伤贡献值最大的车型。因此，最终选取N7车型作为该地区的疲劳代表车型，建立G104国道绍兴段的疲劳车辆荷载模型，如图11所示。

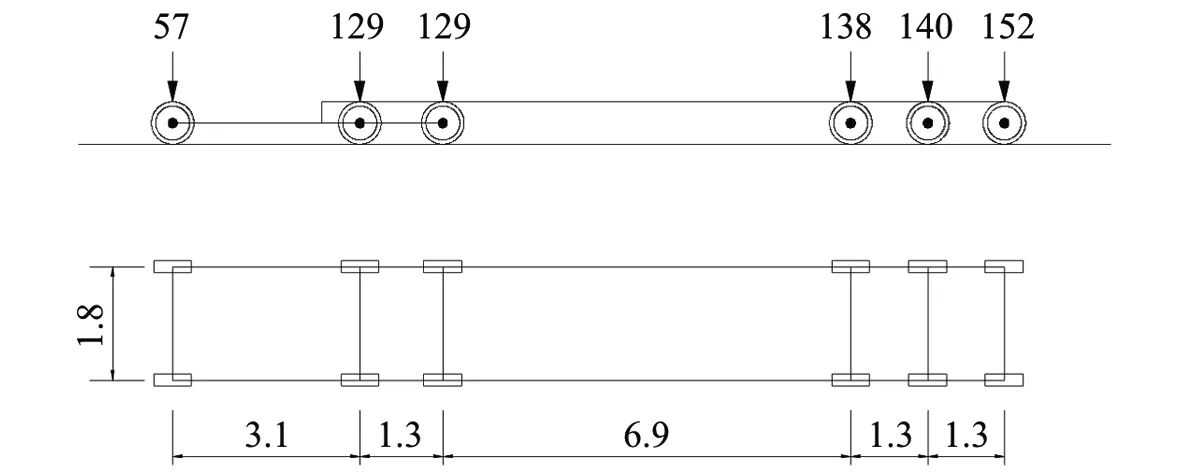
图11 G104国道绍兴段疲劳车辆荷载布置图(轴重力单位：kN；尺寸单位：m)

4 结 语

计算分析表明，各疲劳车型作用下产生的疲劳损伤值大小主要取决于钢筋应力幅值及实际加载循环次数，而钢筋应力幅值主要由疲劳荷载的车型及载重质量控制，实际加载循环次数则与通行荷载的交通流量大小密切相关。损伤度比计算表明，G104国道绍兴段六轴疲劳车N7对结构产生的损伤度最高，最终选取N7车型作为典型疲劳代表车型建立了疲劳车辆荷载模型，可为该地区今后的公路桥梁疲劳设计及验算提供重要的计算参考数据。

公路桥梁交通荷载具有一定的区域性和季节性，本文根据一个月的交通流数据对疲劳荷载展开调查研究，可进一步提取该路段一年的交通荷载数据进行分析，推导得出更加精确的疲劳车辆荷载模型。

[1]JTG D60-2015，公路桥涵设计通用规范[S].

[2]赵建峰.多地域公路桥梁常规车辆及特重车荷载研究[D]. 西安：长安大学，2014.

[3]童乐为，沈祖炎.城市道路桥梁的疲劳荷载谱[J].土木工程学报，1997，30(5)：20-27.

[4]王春生，周江，吴全有，等.既有混凝土桥梁疲劳寿命与使用安全评估[J].中国公路学报，2012，25(6)：101-107.

[5]曾志斌，李之榕.普通混凝土梁用钢筋的疲劳S-N曲线研究[J].土木工程学报，1999，32(5)：10-14.

[6]徐冲，孙晓燕，徐建苗，等.我国公路桥梁疲劳车辆模型研究[J].公路工程，2012，37(2)：22-25.

Research on Highway Bridge Fatigue Load Model in Shaoxing Section of 104 National Highway

ZHAO Jian-feng

(Zhejiang Institute of Communications，Hangzhou 311112，China)

Based on the traffic load data for one month collected by Weigh-In-Motion system in Shaoxing section of 104 national highway，statistical analysis of traffic load characteristic parameters is firstly conducted. Then，according to the fatigue damage equivalent principle, the fatigue load spectrum which is suitable for the highway bridge in Shaoxing section of 104 national highway，is derived from the equivalent fatigue vehicle model. Besides，using a reinforced concrete simply supported T beam of 20 meters as the fatigue calculation model，the fatigue damage degree caused by any fatigue vehicle load is calculated based on the S-N curve and Miner theory. Finally，the highway bridge fatigue vehicle load model is established according to the defined fatigue damage ratio of each fatigue vehicle model. The results shows that fatigue damage caused by fatigue vehicle model of six axis is largest. The fatigue damage value size is closely related to the stress amplitude，which is determined by fatigue load type and loading quality， and also the practical cycles，which is determined by the amount of traffic volume.

highway bridges；fatigue load；S-N fatigue curve；Miner theory

2016-10-27

浙江交通职业技术学院科技研究基金项目(2016YK02)；2016年度浙江省高等学校访问工程师校企合作项目(FG2016012)

赵建峰(1989-)，男，浙江江山人，助教，硕士，E-mail：zjf2014@zjvtit.edu.cn。

U446

A

10.3969/j.issn.1671-234X.2017.01.002

1671-234X(2017)01-0006-06