五年级学生对分数意义的理解

范文贵，郝翡翠

（1．天津师范大学 初等教育学院，天津 300387；2．天津滨海新区塘沽三中心小学，天津 300451）

五年级学生对分数意义的理解

范文贵1，郝翡翠2

（1．天津师范大学 初等教育学院，天津 300387；2．天津滨海新区塘沽三中心小学，天津 300451）

在Marilena Pantziara提出学生掌握分数概念的6个水平的基础上，给出“分数概念理解的3个水平”的思想框架．利用该框架编制测试卷，对天津市564名五年级小学生进行测试，发现：学生在“分数意义”的第三个理解水平较低；学生在“分数意义”各个知识点上表现不同的理解水平；测试总分与5个知识点得分在p<0.01水平上都呈显著正相关，特别是分数的表征（离散量）对总分变量即分数意义的解释程度最高．五年级学生关于“分数意义”水平与总分之间在地区学校方面存在差异性．

分数的意义；小学生；理解水平

1 研究背景

小学分数知识是整数概念的拓展，深层次理解分数概念能够增强学生解决现实世界问题的能力；掌握分数知识结构是学生以后学习小数、比、统计与概率及基本代数运算等的基础．分数的含义可以概括为6个方面：（1）部分与整体；（2）商：（3）子集和集合；（4）数线（number line）上的一个数值或点；（5）比值；（6）公理化定义：有序的整数对：

(p,q)，其中p¹0[1]．分数概念还包含许多子概念，如平均分、单位“1”、分数单位等，而这些子概念又会出现在不同的情境当中，包括离散量情境与连续量情境．

分数概念是小学阶段最难掌握的内容之一．在国际上，分数概念被认为是小学数学学习阶段中最复杂、最容易出现问题、也是最抽象的数学概念[2]．学生学习分数的效果不尽理想，有的学生不理解分数概念的意义，而以机械性的记忆运算法则完成计算．理解分数可以帮助儿童解决更复杂的问题，有助于儿童认知结构达到形式运算水平，并且是儿童日后学习初等代数的基础[3]．

2 研究框架与方法

2.1 研究框架

学生在具体的情景、程序和过程中完成概念建构，再逐渐将它发展为抽象的数学概念，进一步理解符号和概念的本质．Mack推断：学生有丰富的分数直观感觉知识，但是他们难于掌握学校中学习的分数概念及其运算，这是因为他们学习的符号及程序与他们的非正式的知识没有建立联系[4]．在理解分数概念过程中，学生必须能将它放入各种不同的表征系统间；在给定的表征系统内，能很有弹性地处理分数概念；能够很精确地将分数从一个表征系统转换到另一个表征系统[5]．Aristoklis A提出学生理解分数的7个层级水平：（1）认识分数；（2）分数的定义及其数学方面的解释；（3）有关分数的论证和说明；（4）分数的相对大小；（5）分数的表征；（6）分数与小数、百分数及除法的关联；（7）分数问题解决过程中的反思[6]．A. Sfard提出概念形成的3阶段：（1）内化，学生习惯于操作低水平的数学对象的程序，逐渐发展操作这些过程的能力．（2）压缩（或凝聚），在压缩阶段，学生不再关注细节，而是开始能够从整体的角度思考一个复杂的过程．（3）对象的实体化或对象化，即在本质上把握概念．学生能够将形成的具体化的结构与概念的不同形式建立联系，学生构造概念不再依赖于任何过程[7]．与A. Sfard提出的概念发展的3个阶段相关，Marilena Pantziara提出学生掌握分数概念的6个水平[8]：（1）具有程序性理解的特征．在这个水平的学生能够运用简单的一步一步的程序（规则）来计算同分母分数的和．（2）与水平1有着共同的特征，学生也能够运用一步一步的程序来填写两个等值分数中缺失的分子，以及找到两个同分母分数中最大的分数．（3）学生从内化阶段过渡到浓缩阶段认识分数概念．它既需要学生深度的程序性理解，又需要一般化的概念性的理解．例如，在这个水平的学生能够找到一组离散物体中的分数；正确地选出等分割整体中的一个分数．（4）完全具有浓缩阶段的特征．学生能够将一个过程看做一个整体，能够结合不同的过程，能够做出比较以及在不同的分数表征形式间转换．处于这个水平的学生能够结合不同的过程，从给定的数量中重建整体．例如：2/3代表4个物体，找到1/3表示的个数，然后找到3/3代表的个数．（5）从浓缩阶段过渡到物化阶段，学生将分数作为一个抽象的概念．例如：学生能够用多种形式比较两个分数的大小．（6）完全具备物化阶段的特征．学生能够明确分数的一般属性以及各种形式之间的关系，能够在一个对象和一个过程之间转换，能从概念和程序的角度理解分数思想．

在以上研究基础上，结合中国小学分数概念教学实际，给出“分数概念理解的3个水平”的思想框架：（1）学生会运用简单的程序步骤来表示分数概念（如，平均分、确定单位“1”）、把握分数之间可逆关系（如，分数的分解与组合）．（2）辨识不同背景分数的特征；会处理分数的多种表征形式；根据问题需要转换分数的率与量．（3）学生能够结合问题变式条件表征分数；对单位量“1”具有弹性的思考．

2.2 研究方法

（1）文献法：通过分析国内外相关文献，了解分数的不同含义、学生理解分数概念的发展历程、学生学习分数概念可能存在的错误类型及其原因．在此基础上确定研究的问题，明确研究的方向．

（2）测验法：根据教材中分数的意义这节课的内容要求，测试卷包括以下5个方面的内容：平均分、单位“1”、分数的表征（连续量）、分数的表征（离散量）和分数单位．在测试卷设计完成之后，对相应学段的学生进行了预测试，检验其是否合理．

（3）访谈法：根据需要对学生和教师进行开放性访谈，以便作为分析的依据．

除了上述3种方法外，在整个研究中，收集整理问卷测试数据，通过去粗取精、化繁为简以及必要的概括，并且以恰当的形式呈现出来，解释数据蕴含的规律．用平均数、标准差、百分比等描述性统计量表达学生对“分数的意义”3个理解水平．用积差相关分析表达测验总分与5个知识点之间的相关性．用单因素方差分析表达学生对“分数的意义”的理解是否存在区域上的差异．

3 研究问题

研究目的——调查天津五年级学生对分数意义的理解水平，具体研究问题：（1）小学生在“分数的意义”3个理解水平上的表现；（2）小学生在“分数的意义”各个知识点上的表现；（3）测验总分与5个知识点之间的相关性分析；（4）小学生关于“分数的意义”在水平数值与总分之间在3个区（县）方面的差异性分析．

4 研究设计与实施

4.1 研究对象

五年级学生：A学校（天津市内）144人（男：90；女：54）、B学校（天津郊区）259人（男：148；女：111）、C学校（天津县城）161人（男：90；女：71），总计564人．

4.2 测试卷的设计与数据编码及评分方案

测试卷共有16道大题（共20道小题）．题型有填空题、选择题、画图分析题和说明题．对试卷包含的试题进行编码，从第一大题按顺序编码到16大题，分别用1、2、3、…、16来表示．其中第一题包含4个小题，分别用1（1）、1（2），1（3）、1（4）来表示，第八题包含两个小题，分别用8（1）、8（2）来表示，共计20个小题．

在编码方案的基础上制定评分方案，这20道小题每题满分为3分．除3、7、12题之外的填空题和选择题，答对给3分，答错和未作答的给0分．3题第一个空答对1分，答错或未作答0分，第二个空答对2分，答错或未作答给0分；7题第一空答对2分，答错或未作答0分，第二个空答对1分，答错或未作答0分；12题每答对题中的一个要求给1分，共计3分．对于画图分析的题型，13题将图形平均分成3份给1分，画出全部图形的给2分；14题圈出涂黑的圆形的，给1分，填空正确给2分；15题答对给3分，答错和未作答的给0分．对于解释类型的回答，完全正确的解释给3分，不完全正确但讲到关键点的解释给2分，有点正确没讲到关键点的解释给1分，错误的和未作答的给0分．

4.3 测试卷内容和水平的双向细目表及信度分析

测试卷内容和水平的双向细目表和可靠性如表1所示．

表1 测试卷内容和水平的双向细目表

信度分析：测试卷的信度指标 Cronbach’s Alpha为0.791，信度较高，说明这份测试卷有比较好的内在一致性（具体如表2所示）．

表2 可靠性统计量

5 研究结果

5.1 学生在“分数的意义”3个理解水平上的表现

运用SPSS19.0对测试数据处理，得到总分、平均分、标准差、得分率，结果显示（见表 3）：学生在“分数的意义”总的情况平均分为42.48（得分率70.80%），参加测试学生总体成绩不错．学生在3个理解水平上平均分为18.40（得分率87.62%）、12.82（得分率71.22%）、11.26（得分率53.62%）．参加测试学生在“分数的意义”理解水平 1、水平2表现较好，说明学生在理解分数概念过程中，能将它放入各种不同的表征系统间，会运用简单的程序步骤来计算、操作，能够从整体的角度思考一个复杂的过程；而在水平3处于较低水平，说明学生理解分数概念还依赖于具体操作过

程，将分数从一个表征系统转换到另一个表征系统的能力稍差．这与一些研究结果“学生可以机械地比较分数的大小，但要求学生有意义的解释如何比较分数大小却是很困难的”[9]相吻合．

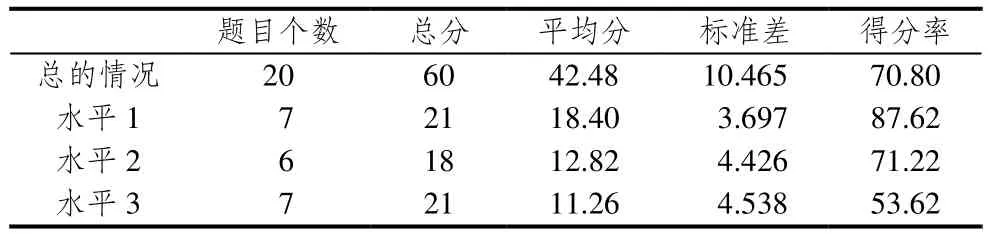
表3 学生在“分数的意义”3个理解水平上的表现（N=564）

5.2 学生在“分数的意义”各个知识点上的表现

从表 4可以看出，学生在“分数的意义”得分率为70.80%，说明学生分数概念的发展是渐进性的，学生可以按程序比较分数的大小，但要求学生有意义地解释比较分数大小的意义是很困难的．学生在“分数的意义”的每一个方面具备相应的特点，其中分数的连续量表征得分率（71.56%）高于分数的离散量表征（64.00%），说明学生解决离散量情境的分数概念问题要比解决连续量情境中的问题更困难，特别是，有的学生不理解分母及分子数字所代表“份数”的意义，对于初学分数概念的小学生来说，要求他们主动想到将两个物体视为一份不是一件容易做到的事情．学生在平均分得分率为 67.00%，学生能够平均分割一般连续量或离散量物体，但是分割后各部分的形状和面积会影响学生建立平均分概念，特别是学生不能对给定的“平均分”图形进行有机整合来正确地表示分数．

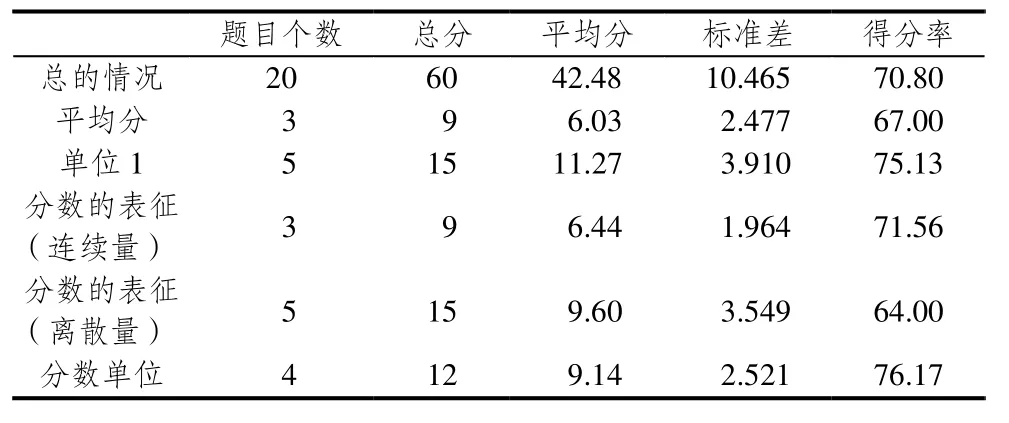
表4 学生在“分数的意义”各个知识点上的表现（N=564）

5.3 学生在“分数的意义”各个知识点上的理解水平表现

5.3.1 学生关于“平均分”在3个水平的表现

学习分数时，学生首先要学会将整体等分割，建立等分的观念是学习分数的基础．从表5看到，学生对平均分的概念的认识是不全面的．在处理水平1分数问题时，学生得分率比较高．解决水平2分数问题时，学生的平分概念不稳固，来自于图示的判断受单一因素影响，缺乏整体的考虑；有的学生只是将具体情境中的整体进行分割而忽略对其平均分割；或者有的学生不按照正确分割标准将整体进行等分割，而只是从视觉上估计是否平均分．在水平3问题，学生得分率较低，显示有的学生会误认为平均分就必须是分割后的每一部分的形状、面积都相同，学生缺乏将给定的图形进行整合重组的能力，以至于无法正确地表示分数．

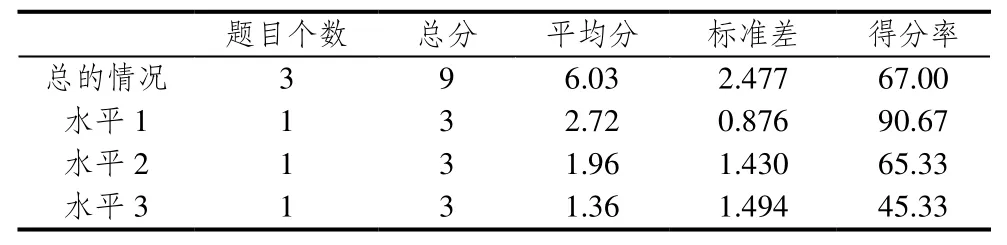
表5 学生关于“平均分”在3个水平的表现

5.3.2 学生关于“单位‘1’”在3个水平的表现

通过访谈几位教师，看到他们能够明确教学目标：理解单位“1”的意义；能够准确把握教学重点、难点：建立单位“1”的概念．总得分率较好．

由具体到抽象，由个别到一般，需要学生在对具体事物感知的基础上让学生认识多个物体可以看成单位“1”．在解决水平2问题：“水果篮中有7个红苹果和5个青苹果，青苹果是全部苹果的（ ）”，需要学生将“7个红苹果和5个青苹果”合在一起，形成12个苹果，构成“单位‘1’”，学生寻找这个隐含的单位“1”有点困难．在解决水平3问题，有的学生倾向于自我假设在同一情境中出现的各个分数具有一样的“单位1”；有的学生自己给出“单位1”，或分解“单位1”．具体见表6．

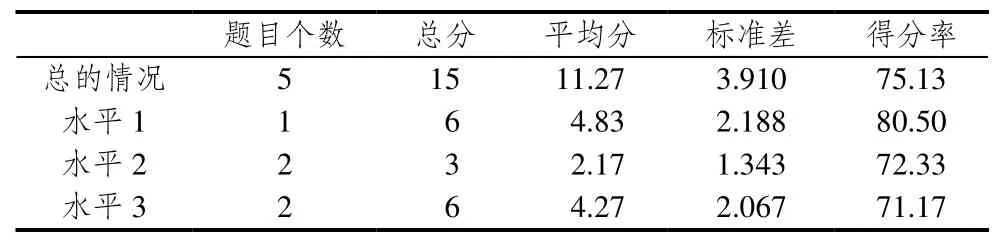
表6 学生关于“单位‘1’”在3个水平的表现

5.3.3 学生关于“分数的表征（连续量）”在3个水平的表现

在“分数的表征（连续量）”部分，水平1问题是比较常见的线段被分割成4份，阴影部分有1份，表示为1 4，问题简单，学生得分率非常高（98.33%）．水平2问题需要学生用语言描述图中分数，有的学生不能用完整的语言表述一个分数代表的实际意义．水平3问题：“下列两个相同的长方形，哪一个的黑色部分面积比较多？（如图）”该题得分率较低（40.67%）．有学生认为：“因为图的形状不一样，阴影部分不一样，所以无法比较”；“因为第一幅图黑色部分是3个三角形，第二幅图黑色部分是3个长方形，所以一样多”．说明学生在比较图形面积的时候，不能与分数的意义建立联系，得不出正确的分数，因此无法比较．

学生关于“分数的表征（连续量）”在3个水平的表现，具体见表7．

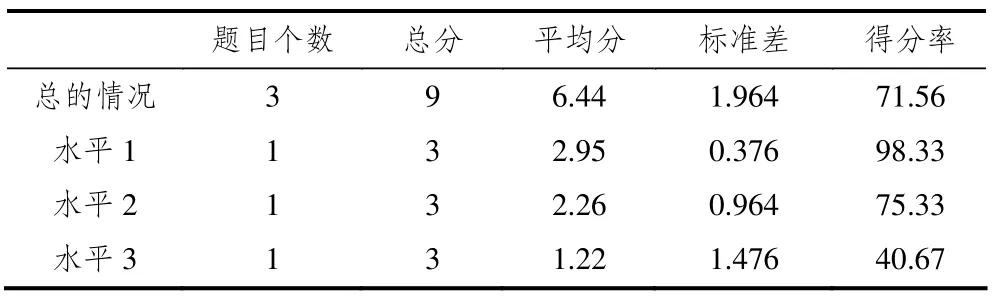
表7 学生关于“分数的表征（连续量）”在3个水平的表现

5.3.4 学生关于“分数的表征（离散量）”在3个水平的表现

在“分数的表征（离散量）”部分，水平1问题“将10个圆片装成一袋，要圈出袋．请问下面哪一幅图是正确的”，大多数学生能够选对答案，学生得分率为79.33%；答错的学生的主要表现：“当离散量的分数问题的分子不是 1时，学生受分子的影响较大”．面对水平2的问题4，学生没有按照题目要求作答，忽略题目中给定的单位1；面对水平2问题14：“圈出下面涂黑的圆形的，那么圈出的黑色圆形是下面全部圆形的几分之几？（如图）”学生得分率为71.17%．有的学生不能正确理解整个分数的含义，把分子看做一组，而并未将分母分组，导致分数表示错误；还有学生将题目中第二问的单位“1”误认为是“4个黑色的圆形”，因此写了．说明学生面对离散量情境不能根据题目中的要求正确确定单位“1”，而是自己确定一个错误的单位“1”来表示分数．学生解决水平3的问题（问题7和13）得分率为49.17%．反映出学生不能理解题目中的信息，不能用分数意义的整体含义来解决问题，特别是学生不能根据题目背景确定单位“1”．学生关于“分数的表征（离散量）”在3个水平的表现见表8．

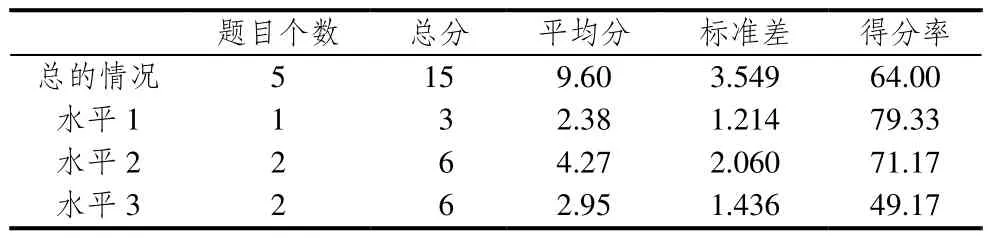
表8 学生关于“分数的表征（离散量）”在3个水平的表现

5.3.5 学生关于“分数单位”在3个水平的表现

在学习分数时，学生必须掌握的要素之一就是建立分数单位．分数单位是造成分数加减能由整数加减来解释、来理解的最重要理由．以分数单位来处理同分母分数的加减法问题，就类似于整数的加减法问题．能理解同分母分数单位加减的概念，就自然而然能够理解异分母分数的加减概念了．

5题和6题考查学生认识分数单位的含义，理解“分数是分数单位累加”，认识到分数也是由“一个个小单位累积”的．这两个题属于水平 1问题，学生得分率比较高（92.00%）．透过分数单位的累加认识分数，为下一步引导学生以整数加减的概念处理分数加减做好铺垫．学生解决水平2问题得分率为72.33%．有的学生不能把分数单位与分数意义建立联系．从整数“自然单位”到“新的分数单位”，这个单位建立的过程是复杂的，有的学生停留在过去处理“自然单位”的学习方法，无法用旧经验来同化处理这个新单位，这是造成学生解决水平3问题得分率较低（48.67%）的原因之一．学生关于“分数单位”在3个水平的表现见表9．

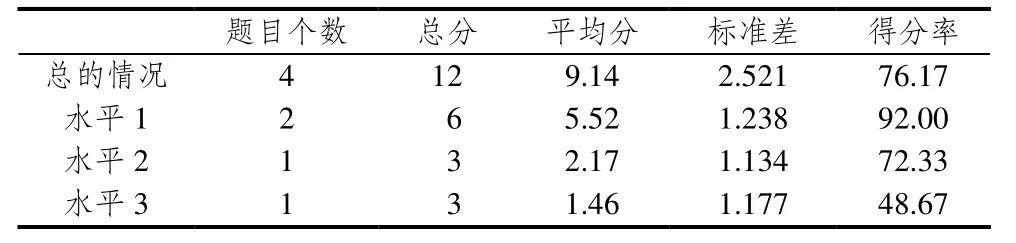
表9 学生关于“分数单位”在3个水平的表现

5.4 测验学生在总分与5个知识点之间的相关性分析

从表10中可以看出，问卷的测验总分与5个知识点以及5个知识点之间在p<0.01水平上都呈显著正相关．其中平均分与单位“1”、分数的表征（连续量）、分数单位之间都呈低度相关关系；分数的表征（连续量）与分数的表征（离散量）、单位“1”、分数单位之间也呈低度相关．分数的表征（离散量）与平均分、单位“1”、分数单位之间都呈中度相关关系；分数单位与单位“1”之间呈中度相关．平均分、分数的表征（连续量）与总分之间呈中度相关关系，单位“1”、分数的表征（离散量）、分数单位3者与总分均呈高度相关关系．上述决定系数2R是积差相关系数的平方，平均分与总分之间的决定系数是0.448，表示平均分变量可以解释总分变量总变异的 44.8%；单位“1”与总分之间的决定系数是 0.585，表示单位“1”变量可以解释总分变量总变异的58.5%；分数的表征（连续量）与总分之间的决定系数是0.340，表示分数的表征（连续量）可以解释总分变量总变异的34.0%；分数的表征（离散量）与总分之间的决定系数是0.637，表示分数的表征（离散量）可以解释总分变量总变异的63.7%；分数单位与总分之间的决定系数是0.533，表示分数单位可以解释总分变量总变异的53.3%．这表明，分数的表征（离散量）对总分变量即分数意义的解释程度最高，其次是单位“1”变量．

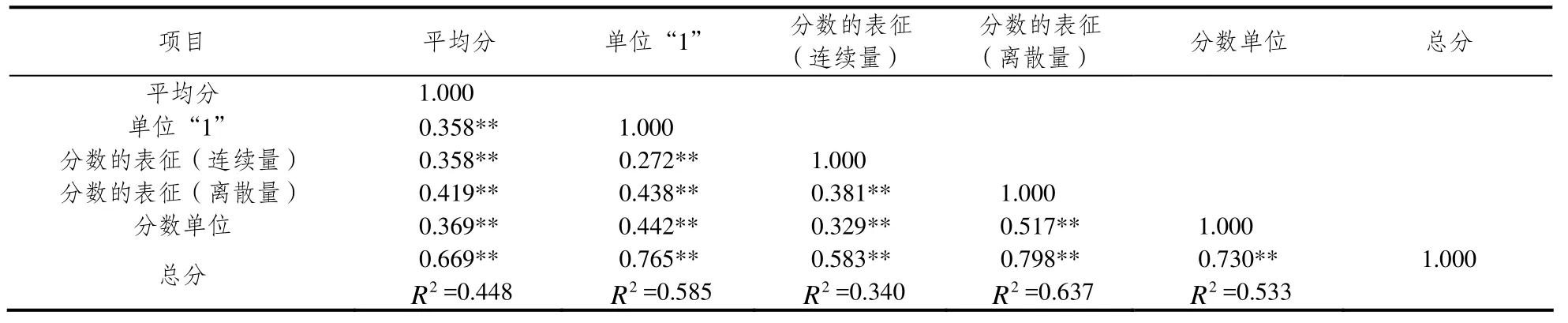
表10 测验总分与5个知识点之间的相关矩阵

5.5 五年级学生关于“分数的意义”在水平分数与总分之间在地区方面的差异性分析

对五年级学生关于“分数的意义”在水平分数与总分进行单因素方差分析，并进行进一步比较，结果见表11．

表11为不同地区的五年级学生在“分数的意义”3水平上的差异比较的方差分析摘要表，从表中可以发现：不同地区的五年级学生在1水平、2水平、3水平和总分之间均有显著性差异，p值均小于0.05．在此基础上进行事后检验可以发现：在1水平、总分方面，天津市内A学校学生和郊区B学校学生的成绩均显著高于县城C学校学生成绩，而A学校和B学校之间无显著性差异．在2水平上，不仅A学校学生和B学校学生的表现均显著高于C学校学生，而且A学校和B学校之间也存在显著性差异，且B学校学生显著高于A学校学生的水平．在3水平方面，采用Scheeffe法事后检验可知，A学校学生和B学校学生的成绩均显著高于C学校学生，A学校和B学校之间无显著性差异．而采用LSD和HSD方法检验发现，不仅A学校学生和B学校学生的成绩均显著高于C学校学生的，而且A学校和B学校学生之间也有显著性差异，且A学校学生显著高于B学校学生的水平．

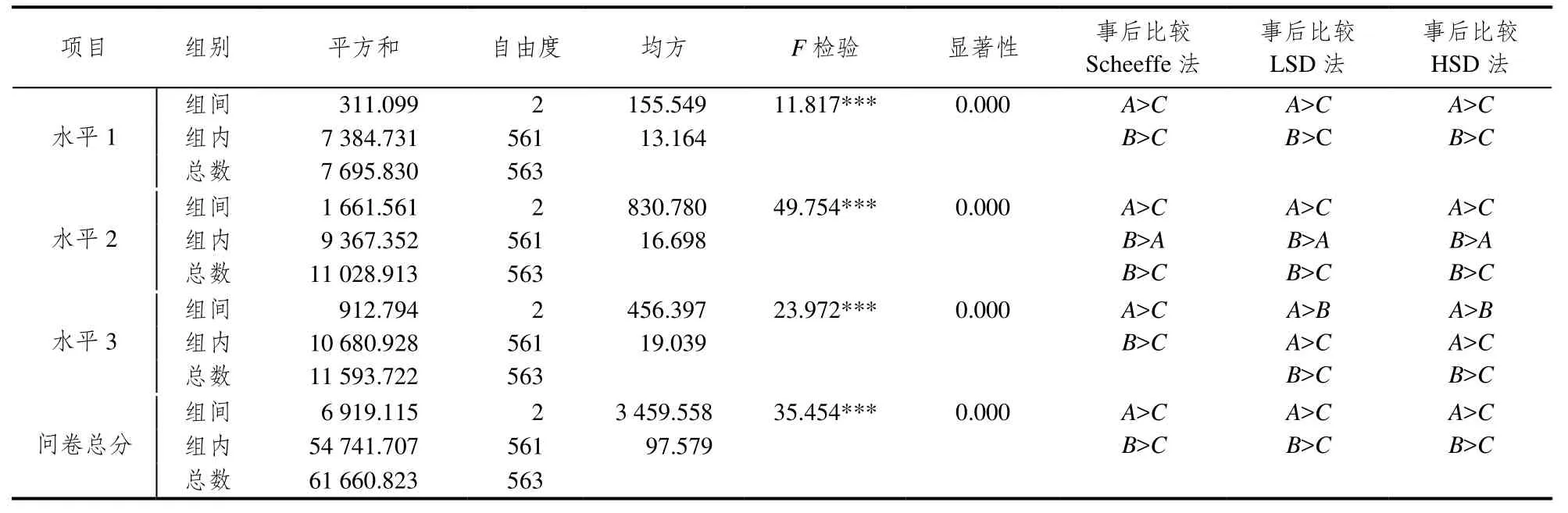
表11 不同地区的五年级学生在“分数的意义”3水平上的差异比较的方差分析摘要

6 教学建议

6.1 强调平均分的概念

教师引导学生在描述分数形成过程，重点强调表示分数的前提就是将整体“平均分”．面对学生解决动态变形背景、不规则图形（第三个理解水平）的平均分问题能力偏低现状，在“3次备课两次反思”的框架下，教师有针对性地设计多样平均分问题，一方面，学生按照规则平均分规则的图形；另一方面，学生学会利用平移、旋转方式重新组合图形，有效解决了学生片面理解平均分意义的困难．

6.2 深度理解分母和分子的意义

教师引导学生将整数的观念过度类推至分数的概念上，将分子与分母做有意义的连结．结合具体案例，帮助学生理解分母表示的是将整体平均分割的份数；利用操作实物或者电脑动画特殊强调：在分数单位内容物是多个的问题背景下，分子表示的是取得其中“一份或几份”（一份可以是一个，也可以是多个）．例如，教师通过比较不同情景中1 4的相同点与不同点，不仅能够发现分数的本质，还能够认识到整体不同会导致分子“1”所代表的物体的个数（或形状大小）不同．分子的“1”表示的是“一份”，而不是“一个”．学生要理解份数与个数之间的关系，以便成功解决问题．

6.3 融入多种表征形式（连续量及离散量）并理解分数概念的本质

从表4可以看出，学生解决分数概念（特别是离散量）问题面临更多困难，有的学生即使能够在课堂上用语言概括分数的意义，但是面对不同的问题情境时，他们仍不能很好地理解分数的意义．教师在教学时注重融入多种表征形式（连续量、离散量），让学生操作具体物，表示各种图形、线段中的分数，用语言概括分数，用数学符号来表征等，通过将多种表征形式相结合，从直观到抽象，逐渐让学生在头脑中建立抽象的分数概念．通过实践活动，学生理解连续量与离散量的关联，避免了随意改变单位“1”而导致结果错误．

6.4 深刻认识单位“1”及分数单位

学生掌握离散情景中（整体是多个物体）的分数的含义，而整体由“一个”过渡到“多个”，需要学生调动高水平的认知过程进行理解．通过多种途径让学生学会找到情景中的单位“1”，逐渐引导学生理解单位“1”既可以表示一个物体也可以表示多个物体．学生理解分子的本质，认识到单位“1”不同会导致分子“1”所代表的物体的个数不同．

不管是整数或是分数的乘除法，都涉及了单位量转化问题，是一种逐渐复杂的单位结构历程，而单位量的转化过程亦可视为以新的参考单位来重新诠释新的数量情境，因此是发展学生基准化能力的关键．

[1]范文贵．分数的内涵有多大[J]．人民教育，2011，（7）：43-47．

[2]Taylor E V, McIntosh C, Gearhart M. Representing Fractions with Standard Notation: A Developmental Analysis [J].Journal for Research in Mathematics Education, 2005, (36): 137-157.

[3]辛自强，张睆．儿童的分数概念理解的结构及其测量[J]．心理研究，2012，（1）：13-20．

[4]Mack, N K. Earning Fractions with Understanding: Building on Informal Knowledge [J].Journal for Research in Mathematics Education, 1990, (21): 16-32.

[5]Charalambos C Y, Pitta-Pantazi D. Drawing on a Theoretical Model to Study Students’ Understandings of Fractions [J].Educational Studies in Mathematics, 2007, 64(3): 293–316.

[6]Aristoklis A Nicolaou. Hierarchical Levels of Abilities that Constitute Fraction Understanding at Elementary School [J].International Journal of Science and Mathematics Education, 2016, 14(4): 757-776.

[7]Sfard A. On the Dual Nature of Mathematical Conception, Reflections on Processes and Objects as Different Sides of the Same Coin [J].Educational Studies in Mathematics, 1991, 22(1): 1-36.

[8]Marilena Pantziara, George Philippou. Levels of students’ “conception” of fractions [J].Educational Studies in Mathematics, 2012, (79): 61–83.

[9]Cramer K A, Post T R, del Mas R C. Initial Fraction Learning by Fourth and Fifth-Grade Students: A Comparison of the Effects of Using Commercial Curricula with the Effects of Using the Rational Number Project Curriculum [J].Journal for Research in Mathematics Education, 2002, 33(2): 111-144.

Understanding the Meaning of the Fraction of Fifth Grade Students

FAN Wen-gui1, HAO Fei-cui2
(1. Primary Education College, Tianjin Normal University, Tianjin 300387, China; 2. Tanggu Third Central Primary School, Tianjin Binhai New Area, Tianjin 300451, China)

Based on the six levels that students grasp concept of fraction proposed by Marilena Pantziara, we give the thinking framework about “three levels of understanding fraction concept”. Using this conceptual framework to devise a test, We have 564 Tianjin Grade five students tested, found: Students’ third understanding level in the “fraction of meaning” is low; Students’ the performance is on the different levels of understanding in the each knowledge point of “fraction of meaning”. The total score of the test was significantly positive correlated with the score of 5 knowledge points onp<0.01 level. In particular, the fractional representation (discrete quantity) is to the highest score meaning interpretation degree. There are differences between the scores level of fifth grade students in schools about “the meaning of fraction”.

the meaning of fraction; pupils; levels of understanding

G622

A

1004–9894（2017）01–0070–06

[责任编校：周学智]

2016–09–20

人民教育出版社课程教材研究所“十三五”课题——小学数学教材国际比较研究（KC2016-006）

范文贵（1965—），男，辽宁锦州人，教授，博士，硕士研究生导师，主要从事小学数学教材比较、小学数学课程与教学论研究．