基于质量检测的初中学生数学建模发展状况的调查研究

李 贺，张卫明

（1．江苏省徐州高级中学，江苏 徐州 221000；2．江苏盐城中学教育集团，江苏 盐城 224001）

基于质量检测的初中学生数学建模发展状况的调查研究

李 贺1，张卫明2

（1．江苏省徐州高级中学，江苏 徐州 221000；2．江苏盐城中学教育集团，江苏 盐城 224001）

数学建模是数学核心素养的基本成分．在2016年江苏省中小学生学业质量监测测试中，对与数学建模相关的题目得分及水平分布作了统计和分析，结果表明：（1）江苏省初二年级学生的6个数学核心素养的发展不平衡，与其它5个核心素养的发展相比较，数学建模优秀水平相对较高．（2）江苏省初二年级学生的数学建模水平发展也不平衡，两极分化现象比较突出．（3）江苏省初二年级学生的数学建模水平表现依次是城区好于镇区，镇区好于乡村；苏中好于苏南，苏南好于苏北；民办学校明显好于公办学校；不存在性别上的显著差异．

数学核心素养；数学建模；初中生；学业质量监测

1 问题提出

数学建模是高中课程标准修订组专家提出 6个数学核心素养成分之一，具体描述为：数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程．主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、构建模型，求解结论，验证结果并改进模型，最终解决实际问题．数学模型构建了数学与外部世界的桥梁，是数学应用的重要形式．数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力．在数学建模核心素养的形成过程中，积累用数学解决实际问题的经验．学生能够运用数学知识求解模型，并尝试基于现实背景验证模型和完善模型；能够提升应用能力，增强创新意识．

模型思想是修订《义务教育课程数学标准（实验稿）》新增的核心概念．《义务教育数学课程标准》对模型思想的描述是：模型思想的建立是学生体会和理解数学与外部世界联系的基本途径．建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果、并讨论结果的意义．这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识[1]．

史宁中教授在《数学思想概论》中提出这样的观点：“数学发展所依赖的思想在本质上有3个：抽象、推理、模型……通过抽象，在现实生活中得到数学的概念和运算法则，通过推理得到数学的发展，然后通过模型建立数学与外部世界的联系．”[2]从数学产生、数学内部发展、数学外部关联 3个维度上概括了对数学发展影响最大的3个重要思想．数学建模过程可以使学生在多方面得到培养而不只是知识、技能，使学生更有思想、方法，也有一些经验积累，其情感态度（如兴趣、自信心、科学态度等）也会得到培养．另外，模型思想还体现在《义务教育数学课程标准》其它方面．如《义务教育数学课程标准》中有如下提法：“经历数与代数的抽象、运算与建模过程．”（数与代数总目标）；“结合实际情境，经历设计解决具体问题的方案，并加以实施的过程，体验建立模型、解决问题的过程”（“综合与实践”内容标准）等[3～5]．那么，当下初中学生的数学建模能力状况到底如何？特别是数学建模作为核心素养提出再次成为数学教育研究的热点，有必要对这个问题作研究．

这里就2016年江苏省初中二年级学生数学学业质量监测中，与数学建模相关的题目得分情况和水平分布作出分析，以反映江苏省初中二年级学生的数学建模水平的基本状况．

2 调查结果

2.1 不同群体在数学建模各水平的分布

图1给出了江苏省及不同群体学生在数学建模各水平上的人数比例．

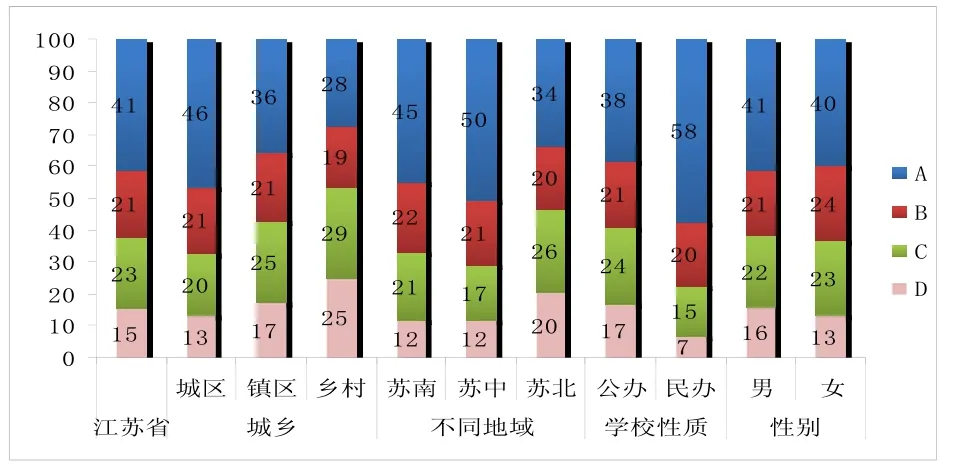
图1 不同群体学生在数学建模各水平上的人数比例

从图1中可以看出，在数学核心素养之数学建模上，江苏省学生在不合格水平上的人数比例为15%，说明江苏省有85%的学生达到了合格及以上水平．城区、镇区和乡村学校学生在不合格水平上的人数比例分别为13%、17%和25%；苏南、苏中和苏北学校学生在不合格水平上的人数比例分别为12%、12%和20%；公办和民办学校学生在不合格水平上的人数比例分别为17%和7%；男生和女生在不合格水平上的人数比例分别为16%和13%．

2.2 题目中涉及数学建模的得分情况

从表1中可以看出，本次测试中，学生总体能力处于A、B、C、D四个水平的学生在M8AO041这道题目上的平均得分率分别是99.2%、97.6%、87.5%、52.0%；从学生的得分分布情况看，在 9个小题中，学生表现优异的小题有 2个，表现中等的小题有6个．表现较弱的小题有1个．

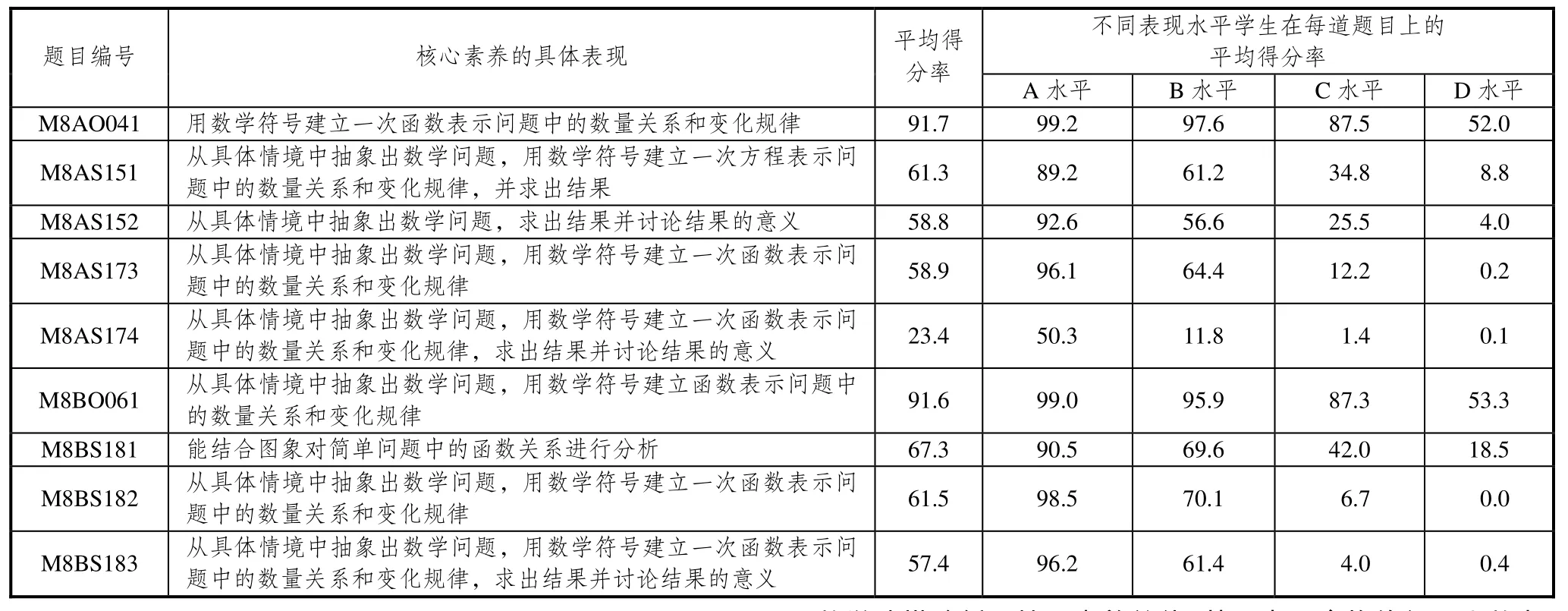
表1 学生在数学建模各题得分的水平表现

3 分析讨论

3.1 不同表现水平学生在每道题目上的平均得分率比较

从调查结果看，学生在以下两个方面表现优异：（1）用数学符号建立一次函数表示问题中的数量关系和变化规律（2）从具体情境中抽象出数学问题，用数学符号建立函数表示问题中的数量关系和变化规律．在以下方面表现较差：从具体情境中抽象出数学问题，用数学符号建立一次函数表示问题中的数量关系和变化规律，求出结果并讨论结果的意义．方程、函数、不等式是刻画现实世界数量关系的模型，用数学符号建立方程、函数、不等式表示问题中的数量关系和变化规律对于大部分学生来说，表现优异．但是对于题目中反应出的复杂生活背境，进而结合函数图象，运用数形结合的思想解决问题是学生的难点．这个结果说明，学生问题解决能力和应用意识值得关注．

4个水平的学生在每道题目上的平均得分率基本呈正态分布，其中优秀、良好水平学生平均得分率低于20%的题有1道，合格水平学生平均得分率低于10%的题有3道，不合格水平学生平均得分率低于1%的题有4道．

3.2 数学建模与6个核心素养总体情况的比较

从两者优秀的得分人数占比看，在所统计的11项数据中，苏南与民办超出3%，另外9项均超出2%，说明对优秀学生来说，数学建模超出核心素养总体情况高度．从两者良好的得分人数占比看，在所统计的11项数据中，数学建模数据均高于核心素养总体，最多低10%，最少低7%，说明对良好学生来说，数学建模低于核心素养总体．从两者合格的得分人数占比看，在所统计的11项数据中，苏南、民办超出 1%和 2%，城区、公办没有差异外，其它数学建模数据均低于核心素养总体的1%，说明对两者合格学生来说，数学建模略低于核心素养总体．从两者不合格的得分人数占比看，从所统计的11项数据看，数学建模数据均高于核心素养总体，最少高出4%，最高高出10%，说明数学建模不合格的学生远超于核心素养总体不合格的学生．

这个结果说明，与核心素养整体的发展相比较，数学建模发展不太平衡，两极分化现象比较突出，这可能与数学建模的题目背境大多来源于生活实际有关，学生“概念性理解”能力强，“问题探究”能力差．

3.3 数学建模自身的差异性比较

城乡比较：从优秀的得分人数占比看，数学建模的表现城区要远好于镇区，镇区要好于乡村；从良好的得分人数占比看，数学建模的表现城区、镇区要好于乡村；从合格与不合格的得分人数占比看，数学建模的表现乡村人数高于镇区，镇区高于城区．

不同地域比较：从优秀的得分人数占比看，数学建模的表现苏中要好于苏南，苏南要好于苏北；从良好的得分人数占比看，数学建模的表现苏南、苏中、苏北大致相当．从合格与不合格的得分人数占比看，苏北的人数要高于苏南、苏中．

不同性质学校比较：从得分人数占比看，民办优秀的人数要远高于公办，合格、不合格的人数远少于公办．

不同性别比较：从优秀的得分人数占比看，数学建模的表现男生略好于女生；从良好的得分人数占比看，数学建模的表现女生略好于男生；而男生不合格的人数又多于女生．

从以上结果看出，男女学生在数学建模水平上没有太大差异．乡村学校和苏北地区的学校初中二年级学生的数学建模水平相对较低，民办学校的学生在数学建模水平方面较许多公办学校更有优势．

3.4 出现的问题分析

对平均得分率为23.4%和61.3%的小题，进行了典型错误的记录，并对错因进行了项目组的讨论与分析．

案例1 M8AS174 水果店张阿姨以每千克2元的价格购进某种水果若干千克，销售一部分后，根据市场行情降价销售，销售额y（元）与销售量x（千克）之间的关系如图所示．当销售量为多少千克时，张阿姨销售此种水果的利润为150元？

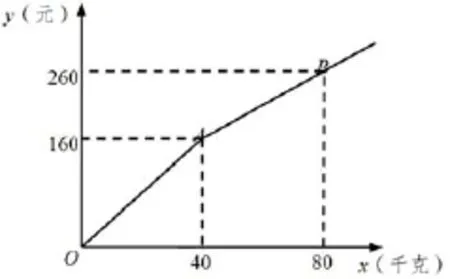
错误分析：

（1）学生没有理解降价前后应是两种不同情况，缺乏分类讨论的意识．

（2）学生错误地将销售额理解为利润，混淆了这两个概念．

（3）学生对降价后的单件利润在函数图象理解上出现错误，或对销售额与利润两个概念理解不清．

（4）学生错误地将降价后的售价理解为直接用 260÷80＝3.25（元/千克），这反应了学生对函数图象不理解．

（5）运算能力不强．

案例2 M8AS151 小丽跟随旅行团到风景区游览．游览过程中，她被景区内的纪念品商店所吸引，用了5 min购物后，立即沿团队行走路线追赶，恰好与团队同时到达距离商店600 m处的景点A．已知她追赶的平均速度是团队行走平均速度的2倍．求团队行走的平均速度．

错误分析：

（1）对数学模型的理解有误，不能正确理解几个变量间的关系，并找到相等关系，不能用代数式表示出相应的量．

（2）不会正确解分式方程，对基本变形如去分母、移项、合并同类项、系数化为“1”等步骤出错，不知道方程每一步变形的依据．

（3）不知道解分式方程要检验，主要是在新课学习过程中，对为什么要检验的理由不理解，对检验的必要性不重视．

4 结论与建议

4.1 结 论

（1）江苏省初二年级学生的6个数学核心素养的发展不平衡，与其它5个核心素养的发展相比较，数学建模优秀水平相对较高．

（2）江苏省初二年级学生的数学建模水平发展也不平衡，两极分化现象比较突出．

（3）江苏省初二年级学生的数学建模水平表现依次是城区好于镇区，镇区好于乡村；苏中好于苏南，苏南好于苏北；民办学校明显好于公办学校；不存在性别上显著差异．

4.2 建 议

（1）建立数学模型的过程，是把错综复杂的实际问题简化、抽象为合理的数学结构的过程．要通过调查、收集数据资料，观察和研究实际对象的固有特征和内在规律，抓住问题的主要矛盾，建立起反映实际问题的数量关系，然后利用数学的理论和方法去分析和解决问题．这就需要深厚扎实的数学基础，敏锐的洞察力和想象力，对实际问题的浓厚兴趣和广博的知识面．

（2）改变过去以教师为中心、以知识传授为主的传统教学模式．教学中应以学生为中心、以问题为主线、以培养能力素养为目标来组织教学工作．

（3）教学过程中要让学生充分体会一次函数、方程、不等式的意义，关注概念、法则、性质等形成的过程，重视法则、性质在解决实际问题中的运用，培养识别图表信息的能力．

（4）加强对学生基本技能的训练，如：解方程或方程组．

（5）将数学与现实、静态与动态结合在一起．教学中不仅关注数学内容的掌握，还特别注重应用意识[6]．

（6）重视数学文化的熏陶，引导学生善于用数学知识和思想方法分析生活中的数学现象．

（7）改变学生的学习方式．数学建模是一个综合性的过程，它具有问题性、活动性、过程性、探索性，因而它不同于单纯的数学解题，这给学生学习方式的改变带来了很大的空间．

[1]中华人民共和国教育部．义务教育数学课程标准（2011版）[M]．北京：北京师范大学出版社，2011．

[2]史宁中．数学思想概论[M]．长春：东北师范大学出版社，2015．

[3]郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1．

[4]喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1．

[5]王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，（7）：50．

[6]何小亚．学生“数学素养”指标的理论分析[J]．数学教育学报，2015，24（1）：13．

Survey on the Development of Mathematical Modeling Capabilities of Junior High School Students Based on the Academic Level Monitoring

LI He1, ZHANG Wei-ming2
(1. Jiangsu Xuzhou Senior School, Jiangsu Xuzhou 221000, China; 2. Jiangsu Yancheng Middle School Education Group, Jiangsu Yancheng 224001, China)

Mathematical Modeling is one of the six mathematical key competences. In this paper, we conducted a survey on the questions related to mathematical modeling and its scores in 2016 Education Quality Monitoring Tests of Jiangsu Province. The data which we collected shows that: (1) there are many imbalances between six mathematical key competences’ training in the junior-middle school students of Grade Two in Jiangsu Province; by comparing with the other five mathematical key competences, mathematical modeling capabilities of the students showed a higher level; (2) the development of mathematical modeling capabilities of the junior-middle school students of Grade Two in Jiangsu Province is lack of balance, which has resulted in the polarization significantly; (3) in particular, the mathematical modeling capabilities of the junior-middle school students of Grade Two in urban areas is better than rural areas; the capabilities of the students in middle Jiangsu is better than in southern Jiangsu, and the later is better than in northern Jiangsu; the capabilities of the students in private-run schools is better than in public-run schools; and there is no significant gap between boys and girls. According to the analysis of the survey above, we finally gave some suggestions to improve the situation.

mathematical key competences; mathematical modeling; junior-middle school students; education quality monitoring

G632

A

1004–9894（2017）01–0019–03

[责任编校：周学智]

2017–01–20

江苏省教育厅基于测试分析的跟进式改革重大研究项目——义务教育学科核心素养和关键能力研究（2015JYKTZD-02）；江苏省中小学教学研究第十一期重点课题——初中数学学业水平评价研究（2015JK11-Z085）；江苏省社科基金——中小学生数学核心素养体系建构与教学实践研究（15JYD001）

李贺（1979—），女，江苏徐州人，中学高级教师，主要从事数学教育研究．