解代数应用题的认知模型建构

张 玲，刘 静

（西南大学 数学与统计学院，重庆 400715）

解代数应用题的认知模型建构

张 玲，刘 静

（西南大学 数学与统计学院，重庆 400715）

问题解决的认知研究一直是热点问题，扎根于数学学科中解代数应用题的重难点教学内容，运用认知分析法，对已有“问题解决”认知研究进行文献梳理与述评，归纳细化出解代数应用题的三维认知过程模型．基于此模型的特点与规律、认知心理学和认知诊断理论，从“操作”和“图式”两大认知成分出发，析出解代数应用题的7个认知属性：基本算术运算A1、多步运算A2、基本数量关系A3、复杂知识的图式A4、识别隐含条件A5、算式表征A6、正规代数策略A7，从而建构解代数应用题的认知结构模型．最后运用口语报告法及流程图分析法来质性评估认知属性及属性间层级关系．为此，将理论反哺于教学实践，为教师数学应用题的有效教学、自上而下测验的编制、以及教师针对学生问题解决的补救性教学提供可操作化的理论基础．

代数应用题；认知过程；认知诊断；认知属性；认知结构

1 引 言

1980年美国数学教师联合会（NCTM）正式提出“问题解决”的观念，指出“数学课程应当围绕问题解决组织……问题解决的成绩将是衡量数学教育成效的有效标准”．而中国2011年颁布的《课标》也将“问题解决”作为重要的四维课程目标之一[1]．解应用题是问题解决的一个重要体现形式，其中区别于算术应用题的代数应用题是小学生问题解决中最突出的重点内容．分析解代数应用题的认知过程能帮助学生深入理解学习的过程，是提高学生解应用题能力的有效途径，亦是教师强化问题解决教学理论的重要路径之一．

对于问题解决的认知研究，不同学者一直莫衷一是，但很难定于一尊．从联结主义桑代克的试误说、行为主义斯金纳的强化说、格式塔柯勒的顿悟说，到信息加工认知心理学的发展，其代表人物纽厄尔和西蒙认为问题包括一个问题空间，即问题的初始状态、目标状态、中间状和所有的算子及步骤构成，问题解决是运用算子，从一个状态转向另一个状态的过程[2]．研究者亦是在此基础上分化出问题解决认知过程的不同阶段．从问题解决的心理机制研究视角出发，归纳具体化解代数应用题的认知过程，基于认知诊断的研究目标，建构解代数应用题的认知模型，运用口语报告法对认知模型进行质性分析验证．

2 数学问题解决认知模型研究述评

通过对国内外与（数学）问题解决认知过程相关的文献整理分析，从主要认知模型间的同异之处和模型研究的发展空间两部分进行综述研究．在此基础上，归纳细化出解代数应用题的认知过程模型，为后文认知结构模型的建构搭建理论桥梁．

2.1 主要认知模型间的同异之处

2.1.1 模型建构均以思维逻辑发展顺序展开

基于认知加工理论建构的问题解决模型，多以其代表人物纽厄尔和西蒙提出的关于问题和问题解决的定义为理论基础．即运用算子，从问题的一个状态转向另一个状态的过程，最终实现从问题的初始状态到目标状态[2]．这个状态的转换过程是以问题解决的思维逻辑发展顺序展开的，符合解决问题的心理发展规律．对于状态转换的描述不尽相同，如杨东从“表征”的视角出发，认为问题解决者内部表征与外部表征不断地进行双向建构的过程[3]．综合言之，对于认知模型均以解决问题的思维过程时间段来进行划分．但是这个思维的过程并不是线性的，当所选择策略无法执行时需重新分析问题制定计划并开展新一轮的认知过程，所以认知模型中阶段间逻辑思维的发展具有非线性的特点．

2.1.2 模型建构的划分阶段虽呈现方式不同但经历大抵相同

在模型的建构中，以阶段划分为主，提炼的结果、呈现方式虽不同，但大抵经历相同．主要可以概括为以下 5个阶段．

（1）审题，即对问题中的文字信息进行理解，明确已知条件、未知条件和各条件间的相关关系．对应为不同研究者提出的问题解决模型中“理解问题”[4]、“读题”[5]、“问题转化”[6]等阶段；（2）分析问题，即分析问题的数量结构和情境结构，从已有认知结构中找到与之相关或许匹配的图式，也即模式识别，问题整合的过程．对应为“分析”和“探索”[5]、“问题整合”[6]、“理解题目”[7～8]、“表征问题”[9]、“问题转移、问题整合”[10]等阶段；（3）计划解题，即组合相关提取出的图式，选择对应的解题策略，制定符合逻辑的解题计划．对应为“制定计划”[4]、“计划”[5]、“解答计划”、[6]“选择算子”[7]、“拟定方案”[8]、问题解决计划[10]；（4）执行计划，即对所制定的解题计划中对应的解题策略验证的过程．对应为“执行计划”[4]、“执行”[5]、“解答执行阶段”[6]、“应用算子”[7]、“执行方案”[8]等阶段．此过程不是一蹴而就的，不同的解题计划会经历不同的往复过程；（5）回顾反思，即对解题过程进行再验证并形成新的认知结构储存于原有认知体系中．对应为“反馈与检查”[4]、验证[5]、“结果评价”[7]、“思路总结”[9]等阶段．

2.1.3 归纳具体化解代数应用题的三维认知过程模型

经过文献梳理，以经典 Mayer的解应用题问题解决的认知加工过程为理论基础，述评已有数学问题解决认知加工模型，综合归纳得出宏观上的解代数应用题认知加工过程为：审题—分析问题—拟定计划—执行计划—反馈反思 5个阶段．再依据Sebrechts等的每个阶段进行细化过程，即个体数学认知结构与特定问题情境之间不断交互作用的动态细化过程[11]，即细化个体由最初已有的图式表征的初始表征状态转换到最终问题的答案的表征过程[3]．建构如图1所示的三维认知过程模型．

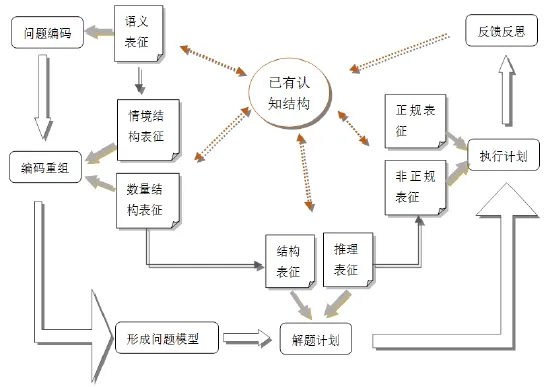
图1 数应用题认知过程模型

2.2 认知模型研究的发展空间

2.2.1 研究对象的具体化以反哺教学实践

数学问题解决过程、解应用题认知过程已有大量研究，取得了较大成就，但仍有可研究的切入视角与空间．对于问题解决的认知过程分析能够带给执教者一定的理论基础，能够揭示问题解决过程中的一般性规律，理论提炼于实践，但如何将理论反哺于实践的研究较少，这也就是为什么一线教师拥有理论却无法用理论指导教学的原因．故研究者从研究对象出发，将学科知识具体化为建构认知模型的研究对象、内容．因数学学习心理有其自身的特殊性，喻平在对《数学问题解决的实证研究述评》中提到，不同的数学知识学习有不完全相同的心理过程，不同的问题解决阶段也有不同的思维形式[12]．基于不同教学内容建构具体化的认知模型不仅对学生问题解决内部心理机制的研究具有重要意义，对教师针对具体内容的问题解决的建构教学模式和选择实践操作策略等的重要性程度亦可见一斑．

2.2.2 研究视角的多元化以提高模型的针对性

综述已有认知模型，以思辨式的建构方法为主．结合实证研究能在一定程度上客观地揭示问题解决的内部心理发展机制，某种程度上又受到如样本的选取、不可控制变量等客观因素的影响和局限．最近不少新的视角方法汇聚至学生问题解决过程研究中，如黑田恭史曾使用真实课堂教学的教学任务，测量学生问题解决过程的脑活动数据，从而获得脑活动与学生理解过程之间的关系[13]；岳宝霞等提出心理学中眼动分析法对数学解题的研究更接近于纯实证研究，有利于探索出培养学生解题的最佳训练策略[14]；另陆珺等也提到在数学认知结构研究领域有些问题无人问津，如没有针对如何测查学生的数学认知结构进行相关深入研究等[15]；基于信息加工理论研究问题解决的认知模型是开辟内部心理机制研究的新出口，而随着计算机科学、认知科学及数理统计等学科不断深入心理与教育测量学领域，建构符合教育测评发展趋势的问题解决认知模型也是应时代之需．作为新一代测验理论——认知诊断理论（CDT），它强调从个体宏观能力水平和微观内部加工过程评估并重，也符合将微观的问题解决过程评估融合入宏观的问题解决能力测评中，为问题解决认知模型的建构和测查学生认知结构提供新的理论视角．

故基于具体化的研究对象——解代数应用题，心理统计的研究视角——认知诊断理论，以及已有问题解决的理论基础，建构解代数应用题的认知结构模型，以为教师数学应用题的有效教学、试卷编制、学生解代数应用题的认知诊断、学生解代数应用题的补救性教学提供可操作化的理论基础．

3 解代数应用题的认知模型构建

3.1 认知模型构建

标准测验理论通常把其所测的宏观心理特质视为一个心理学意义并不明确的“统计结构”，从而导致其测验结果的解释缺乏心理学的证据[16]．同一个问题，不同被试得分相同，但内部心理加工机制以及已有认知结构并不相同，故教师并不能有针对性地给予学生补救性教学．这里基于认知诊断理论建构解代数应用题的认知结构模型．在测量学中，认知诊断是指用于测量个体特定的知识结构（knowledge structure）和加工技能（processing skills）．

3.1.1 认知属性

认知诊断是基于认知加工过程的诊断，是对个体认知加工过程中所涉及的认知属性的诊断（congnitive attribute）．Leighton等认为：“属性”是对完成某一领域问题所需的陈述性或程序性知识的描述[17]．按照功能分类，斯腾伯格认为分析性智力可分为元成分（Metocomponents）、操作成分（Performance components）和知识获得成分（Knowledge-acquisition components）[18]．在此基础上，杨东把信息加工的方法论和因素分析的方法论结合起来，构建了儿童解决数学应用题认知结构模型图（MOSD模型）[3]．（如图2）

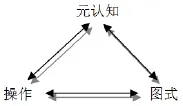
图2 儿童解决数学应用题认知的基本结构模型图

基于认知诊断理论，从MOSD模型的操作成分和图式成分析出认知属性．图式指个体头脑中的知识（包括经验）结构．操作指个体的一种心理运算，是个体对表征符号的一种认知加工．运用认知分析法，即借助认知心理学的研究成果如问题解决、数学应用题问题解决的认知加工过程以及前文建构的解代数应用题的三维认知过程模型等，基于大量文献论证析出解代数应用题的属性（见表 1）．对应属性的可操作性定义见表2．

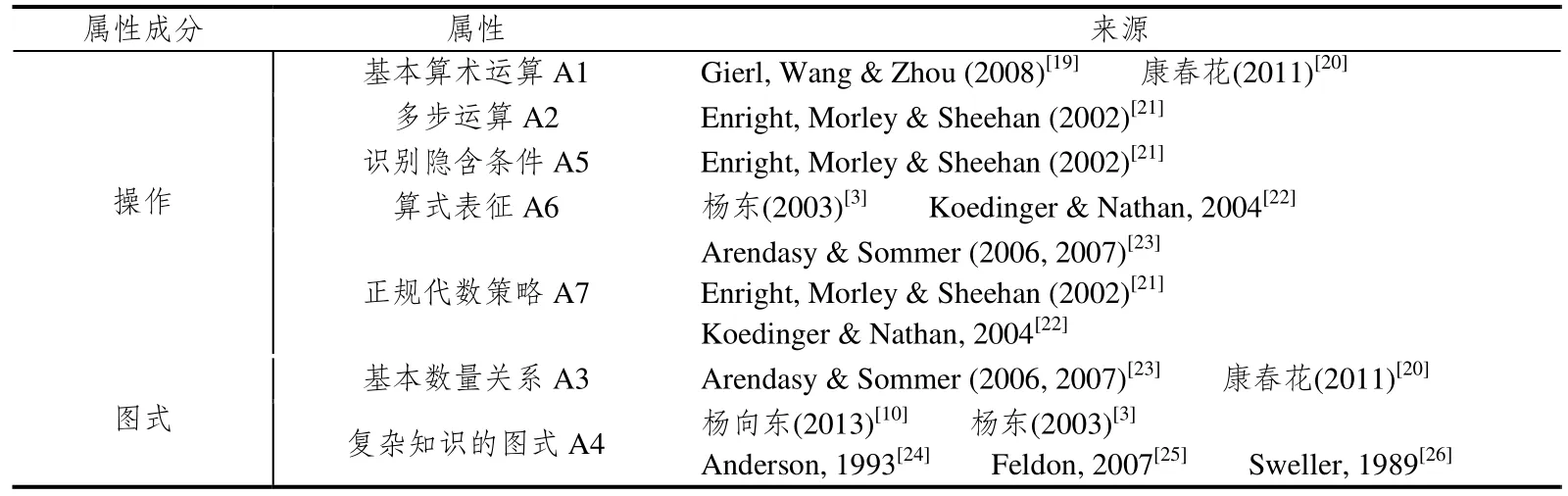
表1 认知属性及属性来源分布

表2 认知属性操作化定义

在操作性属性成分中，“基本算术运算”A1及“多步运算”A2属于个体的运算技能属性，它运用于三维认知结构（如图1）“编码重组”、“解题计划”和“执行计划”阶段；“识别隐含条件”A5贯穿认知结构的前4个阶段，主要为“情境结构表征”和“推理结构表征”；“算式表征”A6主要运用于“解题计划”阶段；“正规代数策略”A7主要运用于“执行计划”阶段．这5个操作属性是个体对借代数应用题时各表征符号的加工技能．在图式属性成分中，基本数量关系A3是“数量结构表征”和“推理结构表征”的基础，而“复杂知识图式”A4是进行“结构表征”的基础，对于复杂知识图式的掌握能大大缩短“解题计划”阶段的进程．

3.1.2 属性层级关系

Leighten等认为认知属性不是独立操作，而是从属于一个相互关联的网络，认知属性间可能存在一定的逻辑顺序或层级关系，认知模型即为用来表征相关任务的属性层级关系图[17]．从解代数应用题的逻辑关联性建构如下的层级关系（见图3）；其中基本算术运算（A1）是掌握属性多步运算（A2）的基础；基本数量关系（A3）是掌握复杂知识图式（A4）、识别隐含条件（A5）和对问题进行算式表征（A6）的前提；对于复杂应用题，需要在A4和A6的基础上运用正规代数策略（A7）进行解答．

在一定程度上属性层级关系体现的是个体心理加工过程中各认知属性掌握的难易程度和认知发展先后顺序，例如多步运算A2操作属性比基本算术运算A1属性更难，而且也需个体在先熟练掌握基本运算的基础上才能掌握多步运算．从三维认知模型（如图1）出发，属性层级关系的逻辑起点是“编码重组”阶段，从操作和图式知识为落脚点，以非线性的方式执行问题解决各阶段．这也将评价个体解代数应用题能力是否存在缺失，落脚到细化的具体的知识属性的掌握上．（如图3）

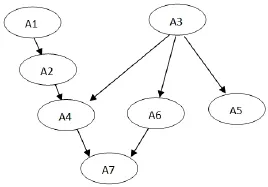
图3 认识结构模型（属性层级关系）

3.2 认知模型的质性验证

运用认知心理学研究中的口语报告法（出声思维），要求被试在进行解答时同步大声思维，以了解被试在作答过程中的思维过程，识别完成任务所需的内容知识与心理过程，验证已析出的解代数应用题的认知属性和建构的认知模型．

3.2.1 被 试

运用分层抽样选取某小学6年级20名学生，20名学生平时数学成绩存在差异．

3.2.2 测试材料

测试材料由出声思维的测试题、进行作答所需文具和录音笔构成．测试题依据所界定的认知属性及其层级关系而编制，共8题．

3.2.3 数学应用题解决的流程图分析

由于篇幅原因，仅呈现其中一个项目（案例1）的分析结果．

案例1：豹子每秒跑31 m，羚羊每秒比豹子慢9 m，一只豹子正在快速追赶奔跑中的羚羊，当距离羚羊150 m时，还需多久能追到羚羊？

案例1中考察了A1（基本算术运算）、A2（多步运算）、A3（基本数量关系）、A4（复杂知识的图式）、A5（识别隐含条件）、A6（算式表征）、A7（正规代数策略）7个认知属性．一类被试完整完成本项目，一类被试仅完成部分，一类被试不会对此项目作答．通过对被试的口头报告和草稿，及作答进行分析，运用Gierl、Wang和Zhou提出的流程图分析法来评估项目的认知属性以及它们之间的层级关系[27]．整理出的典型3种正确作答的认知流程如图4．

（1）被试认知过程特点分析及认知属性认定．

由口语报告及认知流程图的认知过程分析学生解决案例1的基本认知过程特点为：① 问题编码及编码重组阶段：即为对问题的陈述的理解，其中问题语义关系（语义类型）复杂性和问题语言陈述结构的复杂性主要影响个体对问题编码的语义表征[28]．个体首先阅读问题陈述，将每句话表征为对应的文本基，如：“豹子每秒跑31 m”指“豹子的速度=31 m/s”；“羚羊每秒比豹子慢9 m”指“羚羊的速度比豹子慢，值小 9”；第三句指“豹子在后，羚羊在前，豹子在追赶羚羊”；“当距离羚羊150 m”指“豹子在后，羚羊在前，相距150 m”；“还需多久能追到羚羊”指“豹子在追奔跑的羚羊，从两者相距150 m到相距0 m需要的时间”．② 形成问题模型阶段：是在建立情景结构的基础上，运用已有认知结构，形成问题数量结构中各变量之间的具体数量关系，即问题模型[29]．在案例1中，最主要基本数量关系（A3）：路程=速度×时间；最主要的联通架构为：豹子的行程比羚羊的行程多150 m，也为串联起速度与问题目标“时间”的桥梁．③ 制定解题计划阶段：即对问题模型中联通的关系分步制定实施计划，在此阶段某些关系间将直接运用已有认知结构中数量关系进行类比迁移，即结构表征，对应本例中的豹子的行程(未知)=豹子的速度(已知)×追及时间(目标)，羚羊的行程(未知)=羚羊的速度(未知)×追及时间(目标)；例 1中羚羊的速度(未知)=豹子的速度(已知)-9，识别“羚羊的速度”隐含条件（A5）是前提．④ 执行计划阶段：即对制定的计划运用策略实施求解出问题阶段．在案例1中当个体储存了追及问题的图式知识（A4）时，即追及时间(目标)=路程差(150 m)/速度差(9 m/s)=50/3(s)即可；先运用非正规代数策略（A6）表示出羚羊的速度(隐含条件)=豹子速度(31m/s)-9=22(m/s)；然后运用正规策略表征（A7）“豹子行程(豹子速度×相遇时间)-羚羊行程(羚羊速度×相遇时间)=150”，最后运用四则运算法则（A1、A2）等求解最终结果．

（2）属性层级关系验证和典型错误作答分析．

能正确作答该项目的前提是能识别项目为追及问题并且熟知其数量关系：路程差=速度差×时间或情境关系：路程差=豹子行程-羚羊行程，即图式知识（A4）；在此基础上，能够运用数量关系（A3）进行基本变换表示并求取目标变量“时间”亦很重要．对于使用非正规代数策略的被试而言，分为将“羚羊比豹子慢10 m/s”直接表征为速度差，和先通过识别隐含条件（A5）求取“羚羊的速度”再表征速度差，再运用算式表征（A6）列出解答该题的算式．对于使用正规代数策略（A7）的被试而言，熟知图式知识（A4）是前提，再对应表征出豹子的行程=21x，羚羊的行程=(21- 11)x，列出方程，运用基本（A1）和多步运算（A2）计算出最后结果．

在错误报告该项目的被试中，典型的错误表现在：（1）能判别是追及问题并能列式表征，但操作成分中的运算属性未掌握（A1、A2）；（2）能判别是追及问题，但不能列式表征或列方程表征；（3）能判别是追及问题，知道行程问题的基本数量关系（A2）不知追及问题的图式知识（A4），故仅能正确识别并计算隐含条件（A5）“羚羊的速度”；（4）无法作答．

4 教学启示

4.1 自上而下测验的设计

数学教育的本质是构建学生良好的数学认知结构，而要构建良好的认知结构，在教学实践中，教师需要通过各种手段来了解学生原有认知结构，了解其认知结构中的优势和不足，然后才知道教什么和怎么教以完善学生的认知结构[30]．那么如何编制测验项目以评价学生对于解代数应用题问题解决能力上的掌握情况显得尤为重要．同样的测验分数能反馈被试宏观能力水平一致，但不足以评价被试微观上能力的差异．认知模型是测验设计的基石，基于认知结构模型中认知属性的特征以及属性间层级关系，自上而下设计具体考察一个或几个满足层级关系的属性的项目，以确切反馈学生每个项目上属性的掌握情况，正确评价学生无法正确解答项目的原因．

4.2 补救性教学

针对具体学生作答测验的分析，基于认知过程模型，可以从语义表征、情境结构表征、数量结构表征、结构表征、推理表征、正规代数策略表征和非正规代数策略表征等 7个解题认知过程分析学生表征过程及表征过程转化中存在的薄弱点．基于认知结构模型，深入探讨学生问题解决中其知识结构的优势与不足，如具体哪个认知属性掌握不好，并针对这些不足，提出补救性教学建议，因才更因其不足以施教，从而达到补充学生头脑中隐性但可知的所欠缺的知识，有效有针对性地提高每个个体的问题解决能力．

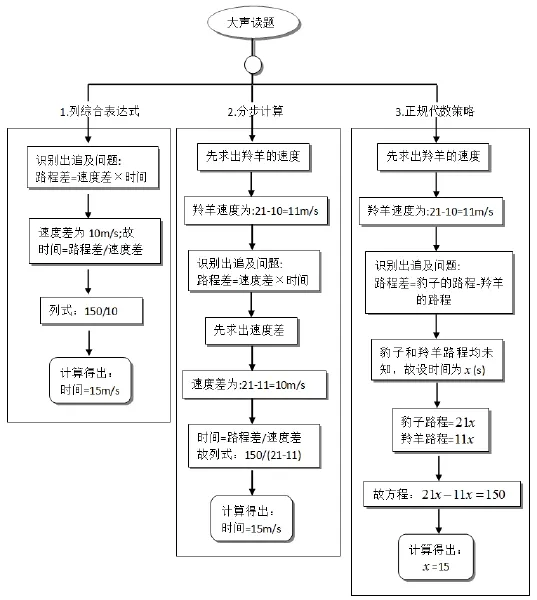
图4 案例1口语报告流程分析

[1]中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：人民教育出版社，2011．

[2]Newell S E, Simon H A.Human Problem Solving. Englewood Cliffs[M]. New Jersey: Prentice-Hall, 1972.

[3]杨东．儿童解决学科问题认知模型的理论建构与实证研究[D]．西南大学，2003．

[4]Polya G.How to Solve It: A New Aspect of Mathematical Method[M]. Princeton University Press Princeton, NJ, 1971.

[5]Schoenfeild A H.Mathematical Problem Solving[M]. Orlando, FI: Academic Press, 1985.

[6]Mayer R E, Hegarty M. The Process of Understanding Mathematical Problems [J].The Nature of Mathematical Thingking, 1996, (1): 29-53.

[7]喻平．数学问题解决认知模式及教学理论研究[D]．南京师范大学，2002．

[8]魏雪峰，崔光佐．小学数学问题解决认知模型研究[J]．电化教育研究，2012，（11）：79-85．

[9]张庆林．当代认知心理学在教学中的应用[M]．重庆：西南师范大学出版社，1995．

[10] 杨向东．代数应用题项目生成中的认知过程与任务特性分析[J]．心理科学进展，2003，（1）：175-189．

[11]Sebrechts M M, Enright M, Bennett R E, et al. Using Algebra Word Problems to Assess Quantitative Ability: Attributes, Strategies, and Errors [J].Cognition and Instruction, 1996, 14(3): 285-343.

[12] 喻平．数学问题解决的实证研究述评[J]．数学教育学报，2002，11（1）：16-20．

[13] 黑田恭史，王立东．脑科学在数序教育研究中的应用[J]．数学教育学报，2011，20（1）：2-4．

[14] 岳宝霞，冯虹．眼动分析法在数学应用题解题研究中的应用[J]．数学教育学报，2013，22（1）：93-95．

[15] 陆珺，喻平．对我国数序认知结构研究的反思[J]．数学教育学报，2010，19（2）：19-22．

[16] 涂冬波．认知诊断理论、方法与应用[M]．北京：北京师范大学出版社，2012．

[17]Leighton J P, Gier M, Hunka S M.Attribute in Tatsuoka’s Rule-Space Model[R]. Poster Presented at the Annual Meeting of the National Council on Measurement in Education, Montreal, Quebec, Canada, 1999.

[18]Sternberg R J.Wisdom and Its Relation to Intelligence and Creatibity[M]. Cambridge University Press, 1990.

[19]Gierl M, Wang C, Zhou J. Using the Attribute Hierarchy Method to Make Diagnostic Inferences about Examinees’Cognitive Skills in Algebra on the SAT(c) [J].Journal of Technology, learning, and assessment, 2008, 6(6): 1-53.

[20] 康春花．小学数学应用题问题解决的认知诊断研究[D]．北京师范大学，2011．

[21]Enright M K, Morley M, Sheehan K M. Items by Design: The Impact of Systematic Feature Variation on Item Statistical Characteristics [J].Applied Measurement in Education, 2002, 15(1): 49-74.

[22] Koedinger K R, Nathan M J. The Real Story behind Story Problems: Effects of Representations on Quantitative Reasoning [J].Journal of the Learning Sciences, 2004, (13): 129-164.

[23] Arendasy M, Sommer M, Gittler G, et al. Automatic Generation of Quantitative Reasoning Items [J].Journal of Individual Differences, 2006, 27(1): 2-14.

[24]Anderson J R. Problem Solving and Learning [J].American Psychologist, 1993, (48): 35-44.

[25]Feldon D F. The Implication of Research on Expertise for Curriculum and Pedagogy [J].Educational Psychology Review, 2007, (19): 91-110.

[26]Sweller J. Cognitive Technology: Some Procedures for Facilitating Learning and Problem Solving in Mathematics and Science [J].Journal of Educational Psychology, 1989, (81): 457-466.

[27]Gierl M, Wang C, Zhou J. Using the Attribute Hierarchy Method to Make Diagnostic Inferences about Examinees’Cognitive Skills in Algebra on the SAT(c) [J].Journal of Technology, learning,and assessment, 2008, 6(6): 1-53.

[28] 涂冬波．小学儿童数学问题解决认知诊断[J]．心理科学，2010，（6）：1 461-1 466．

[29]Kintsch W, Greeno J G. Understanding and Solving Word Arithmetic Problems [J].Psychological Review, 1985, (92): 109-129.

[30] 何小亚．建构良好的数学认知结构的教学策略[J]．数学教育学报，2002，11（1）：24-27．

Research on Building the Cognitive Model of Solving Algebra Word Problems

ZHANG Ling, LIU Jing
(School of Mathematics and Statistics, Southwest University, Chongqing 400715, China)

The research about the cognitive of problem solving has always been a hot topic. In this paper, we focus on the difficult point of teaching content of solving the algebra word problems in mathematic. Through using the cognitive analysis, do comb and review about the existing research about the cognitive of the problem solving, to construct the cognitive process model of algebra word problems. Based on the theory of cognitive psychology and cognitive diagnosis, starting from the two cognitive component of operation and schema, we has precipitated seven cognitive properties of algebra word problems: basic arithmetic operations (A1), muti-step operations (A2), basic quantitative relationship (A3), complex knowledge schemata (A4), recognition the implied condition (A5), formula characterization (A6), formal algebraic strategy (A7), to construct cognitive structure model of algebra word problems; Finally we use oral report method and flow chart analysis to qualitatively evaluate the cognitive properties and the hierarchical relationship between attributes. Therefore, feedback the theory in teaching practice, for teachers’ effective teaching of mathematics word problems and the preparation of the top-down test, and provide the theoretical basis for teachers’ remedial teaching.

algebra word problems; the cognitive process; the cognitive attributes; the cognitive structure

G40-03

A

1004–9894（2017）01–0064–06

[责任编校：周学智]

2016–09–29

张玲（1991—），女，湖北黄冈人，硕士研究生，主要从事数学教育心理统计与测评研究．刘静为本文通讯作者．