勾股定理教学实验研究——让学生真正经历勾股定理的“再发现”过程

吴增生，郑燕红，李宏彦，陈娅芬

（1．浙江省仙居县教育局教研室，浙江 台州 317300；2．浙江省仙居县安洲中学，浙江 台州 317300）

勾股定理教学实验研究
——让学生真正经历勾股定理的“再发现”过程

吴增生1，郑燕红2，李宏彦2，陈娅芬2

（1．浙江省仙居县教育局教研室，浙江 台州 317300；2．浙江省仙居县安洲中学，浙江 台州 317300）

勾股定理是数学中的重要定理，教学中要力求让学生进行自然合理的再发现活动，渗透数学文化．通过以下两项任务引导学生进行探究活动：（1）用大小相同的正方形纸片剪拼成一个大正方形；（2）用大小不同的正方形纸片剪拼成一个大正方形．让学生在类比任务（1）的基础上完成任务（2），在解决问题的过程中自然发现勾股定理．把这种教学方案与采用传说中的毕达哥拉斯发现勾股定理方法的教学方案进行教学对比实验，结果表明：新的教学方法学生的发现感更强，对发现过程的记忆效果更好．

勾股定理；教学实验；再发现

勾股定理是平面几何中的重要定理，它在数学发展史上的赫赫地位使其成为初中数学教育中开展探究活动，渗透数学文化的重要素材．勾股定理教学中只让学生知道结论并会套用是远远不够的，需要让学生深入思考、探究发现，并结合内容进行数学文化教育，实现数学育人．

1 问题提出

中国数学教材中“勾股定理”的呈现方式主要有这以下几种：第一种方式是直接给出命题并用直角三角形相似知识加以证明，这在早期重视平面几何公理化体系的教材中比较多见[1～2]；第二种方式是采用让学生直接测量直角三角形三边的方法发现勾股定理[3～4]，第三种方法是先用测量三角形三边长方法发现结论，再介绍用如图1、图2的正方形面积计算方法证明结论[5]；第四种方式是先在网格中计算正方形面积，发现3个正方形的面积之间关系，再用面积法进行证明或验证[6]；第五种方式是直接让学生用4个全等的直角三角形拼图，用边的运算表示面积关系，通过运算发现勾股定理，如浙江教育出版社2012年版的教材要求学生用直角三角形拼赵爽弦图，通过面积计算发现勾股定理，青岛版（2012版）则让学生用4个直角边长分别为a，b的直角三角形拼边长为a+b的正方形，通过面积计算发现勾股定理．

日本教材《中学数学》中先让学生探索直角三角形三边上的正方形的面积关系来发现勾股定理，再用如图1的方法证明结论；新加坡的数学教材New Mathematics Counts则是介绍如图3的拼图方法发现和证明勾股定理[7]．

由于第一种方式太过强调公理化思想，有“掐两头烧中段”的味道，没有让学生经历勾股定理的发现过程，在现行的各种版本教材中基本不用；第二种方式因为这种测量方法本质上不可能发现一般意义上的勾股定理结论，假探究的味道很浓，因此现在也很少采用．现在基本上采用后3种呈现方式，其中第三种方式是第二、第四两种方式的兼顾与综合，其主要思路应该归结为第四种方式．

但是，第四、五两种方式在教学过程中仍然存在着问题，教师教学起来不自然、不流畅，很难真正让学生经历自然合理地发现问题、提出问题、分析问题和解决问题的过程，缺乏真正的“再发现”教育价值．例如第五种方式，让学生用4个全等的直角三角形拼如图1，图2的图形，通过内外两个正方形面积和4个全等的直角三角形面积关系的计算（用直角三角形的三边相关字母表示）来发现勾股定理，就会产生这样一个问题：“为什么要用4个直角三角形拼正方形”？其实，这种方法可以用来证明勾股定理，但用来发现勾股定理，显然有些牵强．第四种方法，先让学生观察网格中的等腰直角三角形，发现其以三边为边长的正方形面积之间的关系，提出等腰直角三角形三边关系，再推广到一般，在网格中用割补法计算以一般直角三角形三边为边的正方形面积之间的关系（如图4，图5），从中发现一般的直角三角形三边关系的猜想；再用如图1和图2来验证或证明，或者用正方形面积剪拼来证明（如图6）．

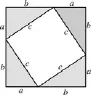
图1

图2

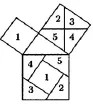
图3

图4

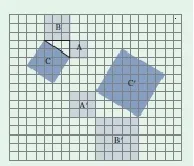
图5

图6

用这种方式组织教学，学生可以从特殊到一般地发现直角三角形三边的平方关系，但是，从这种思路自然发展延伸出来的任务是要证明直角三角形的斜边正方形面积等于两直角边正方形的面积，其自然证法应该是欧几里得（Euclid,约公元前300年）的证法（如图7）．由于证明过程要用到正方形性质（这是后继学习内容）、全等三角形、等积变换等，比较复杂，学生难以接受，所以教材转而介绍赵爽证法，这样，发现结论和证明结论是两种不同的思路，思维不连贯，思考不自然．还有，按照这种教学方式组织教学，本质上是教师带着学生“看图形”，缺少自然合理思考和发现的味道，这种探究的“发现味”不足．而该教学实验后的问卷调查数据分析也说明了教师这样组织教学，学生在学习过程中的“发现感”不强，对发现过程的记忆不深．新加坡教材中的方法由于图形分割方案太复杂，思路太特殊，学生难以想到．

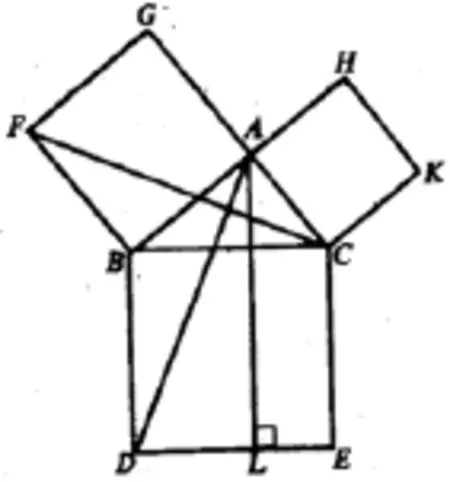
图7

因此，需要探索一种更合理的教学设计，引导学生在自然合理地提出问题、分析问题、解决问题的过程中自然发现定理，让大脑体验成功发现的“A Ha！”快感．

2 教学改进研究：设计更合理的学生再发现活动

2.1 数学史和脑科学的启发

几乎所有的文明古国都发现了勾股定理的结论，而且从史料上看，早期勾股定理的发现和证明几乎都与正方形的面积割补和转换有关．

西方普遍认同把勾股定理的发现证明归功于毕达哥拉斯学派，在古希腊文献里面最早提到毕达哥拉斯跟几何有关系的是古希腊作家和哲学家普路塔克（Plutarch，约公元前46—120）．普路塔克说毕达哥拉斯因为发现了一个重要的几何定理，杀了100头公牛来献祭，他没有说是什么定理，说毕达哥拉斯发现并证明勾股定理，这是传说，缺乏史料证据．普路塔克还介绍了用正方形面积割补证明勾股定理的方法．如图8，设直角三角形的两直角边长分别为a，b斜边长为c，以此三角形为基础，作两个边长为a+b的正方形，根据大小正方形面积和三角形面积之间的关系，得到，得到[8]．

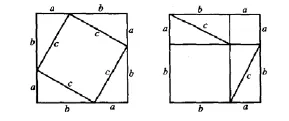
图8

比普路塔克更早的欧几里得采用如图 7的方法证明勾股定理（《原本》中的命题47，只给出3个正方形的面积关系）．中国古代几何学中，面积方法应用得很出色，总结出的面积“出入相补”原理运用到许多几何图形的研究中，而著名的勾股定理的赵爽证法（如图9）就是这一原理的经典应用[8]．

用正方形面积割补方法发现和证明勾股定理，无需太多的知识储备，是一种直观、简约而自然的思考方式，它能使发现和证明思路连贯，可以设计教学活动的基本思路．

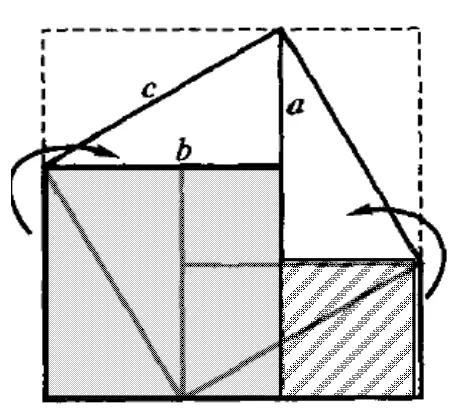
图9

虽然与发现勾股定理的古人相隔几千年，但对于进化进程来说，则是相当短暂的，当代人类与几千年前的人类的大脑生理结构差异微小，而且，人类个体的大脑思维活动经验可以通过基因的表达遗传给下一代，因此，大脑的神经功能在不断的代际遗传中得到发展．而更重要的是，人类可以通过文字媒介把思维活动经验和结果直接记录并在后代传播，从而让后人能更便捷地积累知识和思维经验．这样，通过遗传和思维经验的直接传递，古人思考问题的大脑活动可以在现代人类思考相同问题的大脑活动中表现出相似性，这是数学思考历史相似性的脑科学原理，也是基于数学史设计教学活动的依据．

在这些经典的勾股定理证明思路中，赵爽弦图（图9）问题自然、目标明确、思路清晰，而且更便于动手操作，因此，赵爽的方法更便于学生的探索和发现．但赵爽的方法思路学生还是难以想到，需要设计更有效的“脚手架”帮助学生更自然合理地思考．设计逐步深入的两个任务：（1）用两个相同的正方形及其内部剪拼成一个大正方形及其内部；（2）用两个不同的正方形及其内部剪拼成一个大正方形及其内部．引导学生通过类比把简单问题研究的经验迁移到变化的情境中．这是比较自然的教学设计，只所以说这种方法自然，是因为它符合了“大脑总是通过重复或修饰已有反应模式来预测和适应新的环境，而反应模式的修饰遵从贝叶斯原理”这一基本规律[9]．

2.2 教学改进方案设计

介绍几何学起源于古代土地测量和图案设计，指出面积问题是古代几何学研究的一类重要问题，而正方形面积是最简单的图形面积．接着出示任务1：用两个边长相等的正方形纸片，让学生把它剪拼成一个大正方形（如图10）．

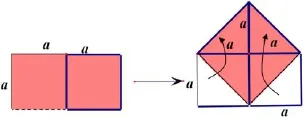
图10

在学生完成任务1并进行反思总结和再给出任务2：再让学生把两个大小不同的正方形纸片剪拼成一个大正方形（如图11）．

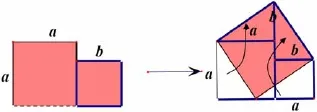
图11

在学生完成任务1后，对探究操作过程进行如下分析，以便为学生完成任务2提供启发线索：在任务1中，是怎样想的呢？是先通过连接两个小正方形的对角线把正方形等分成两个全等的三角形（如图10右），这样做的目的是找到拼成的大正方形的边，根据小学学过的正方形定义（4个角都是 90º，四边相等），因此，确定的邻边既要相等又要互相垂直，而如图10右边的图这样连接两个正方形的对角线则恰好能满足这两个要求．

在学生进行任务2前，需要引导学生类比任务1，比较两者的相同点和不同点：相同点是都要求用两个正方形纸片剪拼成大正方形（总面积不变），不同点是两个正方形从大小相同变成了大小不同，怎么办？引导找到下面边沿上的适当一点，构造大正方形的一对邻边（如图11）．这样，学生能自己找到从两个连体正方形的下底边上找到恰当的分割点．在学生完成每一个任务后，对拼图过程进行几何画板动画展示，加深学生的认识．

在学生完成上述两个任务后，引导学生把这种面积数量关系转译成直角三角形的三边关系，这样，由于学生可以从易到难地通过类比形成探究思路，学生就可以自然发现勾股定理的结论．

在学生发现勾股定理后，组织学生辨别勾股定理的内容，介绍相关的数学史及不同的证明方法，介绍传说中的毕达哥拉斯发现勾股定理的过程和赵爽弦图，比较该方法发现的勾股定理及证明，实质上与赵爽的证明方法相同．让学生体会自己发现的价值，学习数学文化，享受发现的快乐．在此基础上，让学有余力的学生在课外自己书写出勾股定理的证明过程，查阅勾股定理证明的相关文献．

3 教学对比实验过程

3.1 样本的选择

在浙江省仙居县安洲中学选择3个平衡班A、B、C，这 3个班级近 3个学期的期末考试成绩总体平均分用SPSS19.0进行独立样本的均值t检验，结果如表1—4．

表1 各班3个学期期末考试成绩均值及标准差

表2 A班B班均值t检验结果

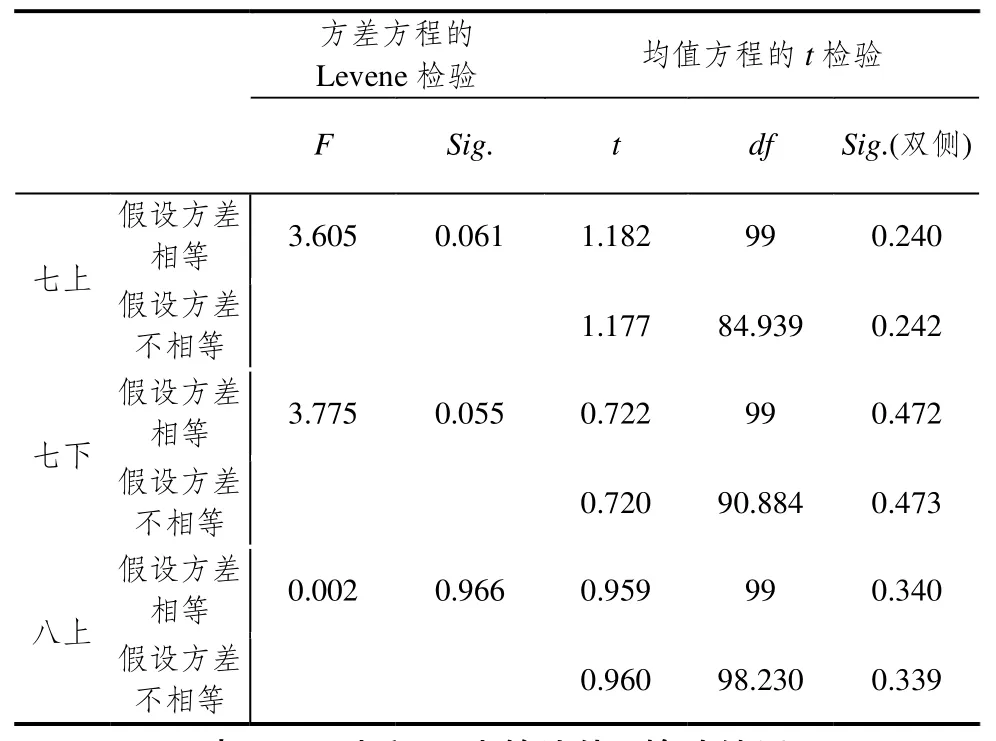
表3 A班和C班均值t检验结果

表4 B班和C班的均值t检验结果

经检验，A、B、C班3个学期的期末考试成绩的均值检验中Sig值均大于0.2>0.05，因此没有显著性差异．

A、B两个班级为实验班，C为控制班，实验班采用改进后的教学方案进行教学，其中 A班由研究者亲自实施教学，B班由任课教师在学习并观摩研究者教学后自己去实施教学，C班则在教师观摩研究者教学前由教师本人按照人教版教材中的内容呈现方式实施教学．实验过程进行录像，拍摄学生拼图的照片，实验后进行问卷调查，问卷的题目是：

问卷中的问题 1是为了解学生在不同的教学方法下对自己的发现感的评价；为了进一步明确学生是否真的是自己发现定理的，采用问题2通过让学生回顾发现过程及发现时所用的典型图形来进行确认，若学生能完成回忆起操作步骤及典型图形，说明学生是经过自己的操作和思考经历了再发现过程．

4 效果分析

4.1 实验过程分析

教学实验过程中，学生完成任务1用了6分钟，对方法总结用了3分钟，而在进行任务2操作前，教师进行5分钟的分析引导（主要强调类比，比较任务1和任务2的相同点和不同点，把任务1中先确定拼成的大正方形一组邻边的方法迁移到任务 2，再分析方案的不同点，确定剪拼方案），然后让学生独立思考和相互合作进行剪拼活动，用时20分钟．介绍数学史用时3分钟，解决勾股定理的实际应用问题“已知一旗杆的影子长为3 m，阳光光线与地面夹角为60º，求旗杆高度”，体会勾股定理的价值，让学生知道已知直角三角形中的两边长可以求出第三边的长，用时3分钟；课堂小结用了3分钟．教学过程中，大部分学生能自己独立或与同伴合作完成两个拼图任务，快的学生在任务 2中用了 6分钟，慢的则用了20分钟．

下面是A班学生课堂探究中拼成正方形的两张照片（如图12）．

图12

4.2 问卷调查分析

对于问卷中的两个问题的数据分析如表5.

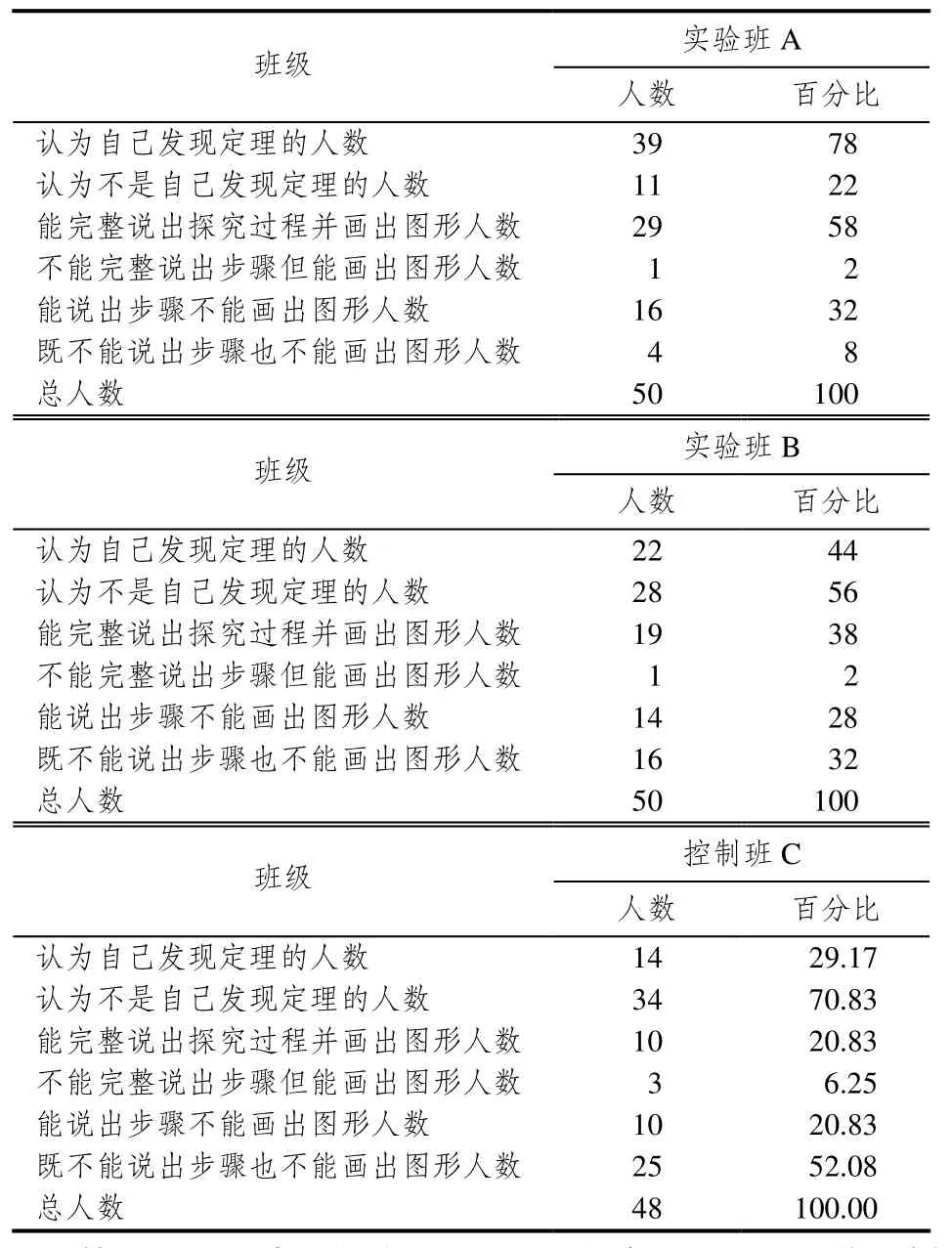
表5 问卷调查统计分析

从中可以看出，实验班A、B认为自己发现定理的比例比控制班C分别高出近50%、15%，实验班A、B能完整回忆起探究步骤并能画出关键图形的比例分别比控制班高出37%、17%，实验班A、B能说出步骤不能准确画出图形的比例分别比控制班高21%和7%，实验班A、B不能说出步骤也不能准确画出图形的比例分别比控制班低44%和20%．

此时的公共空间则象征性地存在于贵族行为和个人行为上，已不再像是古希腊时期所呈现的个人自我价值实现的意义场所。“在那里它们只有私人的重要性，从而真正的公共领域荡然无存”[6]。公共空间只是领土主权的权利表达，不再能把国家和人民相互联结起来。教堂和其附属的广场充当了人们的公共空间，教会占据了人生活的一切，控制着人的活动，这使孕育体育运动的土壤逐渐消逝。人自身受到挤压，人的权利、地位、历史都在此失去色彩。庆幸的是，随着商品贸易和信息的全球化，人逐渐走向自我觉醒和解放，人的公民意识开始建立在公众的共识上，开始营造平等、自由、公开的公共交往，这为塑造更人性的公共空间提供了前提条件。

对于能说出探究步骤并能画出典型图形，能说出探究步骤但不能准确画出典型图形，不能说出探究步骤但能画出典型图形，不能说出图形也不能画出典型图形的学生分别赋分5、3、1、0，在收集数据后用SPSS19.0软件进行独立样本的均值t检验，结果如表6—9．

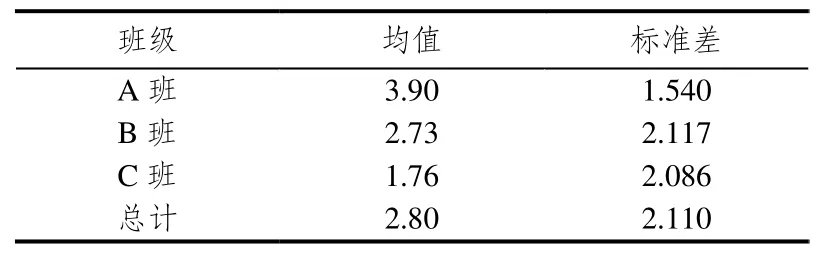
表6 各班问卷调查赋分成绩均值和标准差

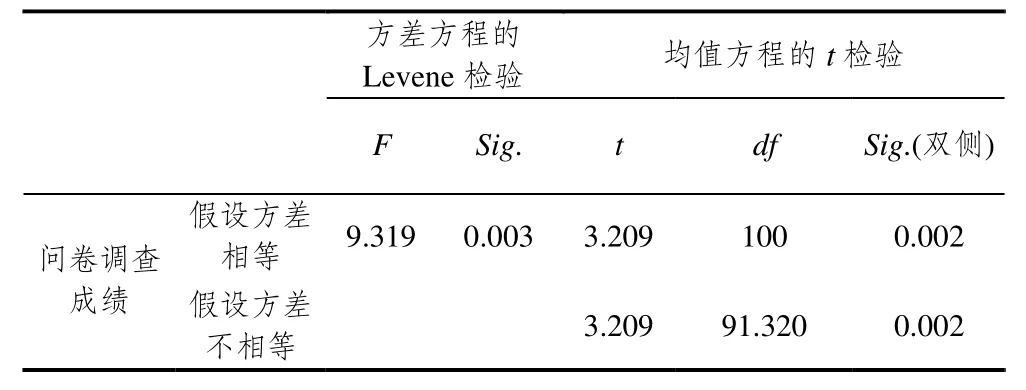
表7 A班和B班问卷调查赋分均值t检验结果

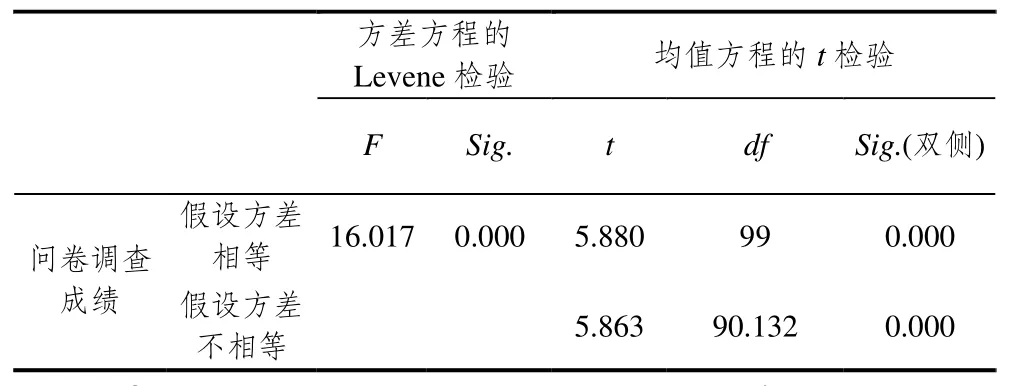
表8 A班和C班问卷调查赋分均值t检验结果

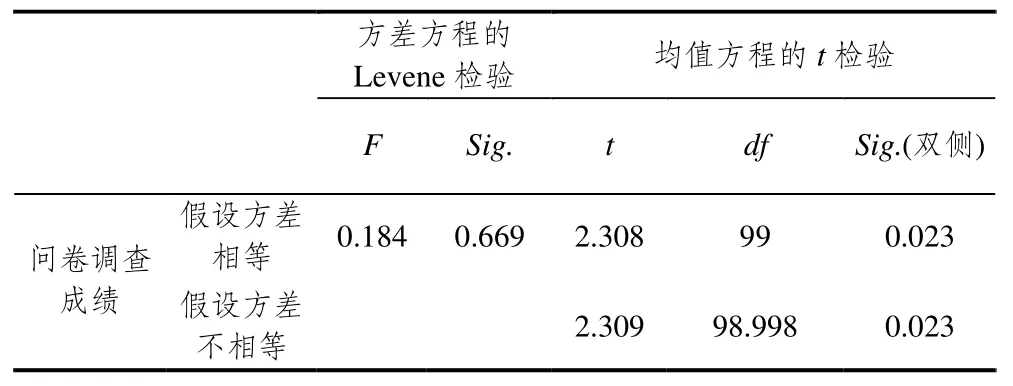
表9 B班和C班问卷调查赋分均值t检验结果

表7、表8和表9中的Sig值都小于0.05，说明3个班级问卷调查的赋分成绩均值有显著性差异．

上述数据表明采用改进方案进行教学，学生认为自己发现定理的人数多了，能回忆起探究步骤和图形的人数多了．在实验班中，也有学生创新性地应用三角形版辅助设计方案，其作品如图13．

图13

实验班和控制班学生问卷中回忆出的探究发现勾股定理的典型图形如图14和15．

实验班A和B（如图14）：

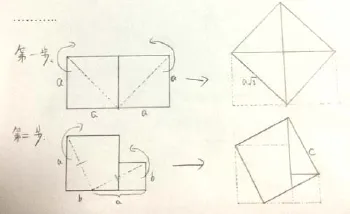
图14

控制班C（如图15）：

图15

4.3 讨 论

从问卷调查分析可以看出，A班效果好于B班，B班效果好于C班．由于A班由研究者亲自执教，对于难点的引导和启发比较到位，这样，学生能较为顺利地从任务1的操作中提取探究经验并迁移到任务2中去，B班由原任教师执教，在教学中对难点的启发不够到位，影响了学生任务 1的经验形成和迁移，效果与A班有差异．但是，由于B班和 C班是同一个老师用两种不同方法进行教学，其学生表现出的差异更具有说服力．问卷调查结果表明，采用改进设计后的教学方案，能有效改善教学效果．

改进设计后的教学能有效改进教学效果，其原因是：

（1）任务简单自然，把两个相同的正方形剪拼成一个大正方形，由于在人教版教材七年级下册的实数一章中已经做过，有经验支撑，是原有经验的提取，容易完成，从任务1到任务2是问题的一般化，其发展也是极为自然的．而且，由于课堂中只有两项任务，减少了课堂容量，从而学生的探究和思考时间更加充分（学生自己探究时间超过26分钟）．

（2）任务之间有内在必然的关联，任务1的探究活动可以为任务2操作积累有效的活动经验，这种基于任务的类比探究可以帮助学生形成并迁移拼图活动经验．

（3）探索发现和证明思路连贯，探索发现的过程能启发证明（验证）的思路，这样便于学生自然合理地分析和思考．

（4）学生学习过程是真正的发现问题、提出问题、分析问题和解决问题的探索发现和验证的过程，通过自身探究发现的知识更容易被理解和记忆．

[1]刘熏宇．高级中学课本平面几何[M]．北京：人民教育出版社，1954．

[2]余元庆，奚今吾，管承仲，等．高级中学课本平面几何[M]．北京：人民教育出版社，1955．

[3]北京市中学数学试用课本第一册下册[M]．北京：北京人民出版社，1977．

[4]范良火．义务教育初中数学实验教科书（八年级上册）[M]．杭州：浙江教育出版社，2006．

[5]马复．义务教育教科书·数学八年级上册[M]．北京：北京师范大学出版社，2013．[6]林群．义务教育教科书·数学八年级下册[M]．北京：人民教育出版社，2013．

[7]朱哲，张文忠．中日新数学教科书中的勾股定理[J]．数学教育学报，2011，20（2）：84-87．

[8]李文林．数学史概论[M]．北京：高等教育出版社，2011．

[9]Chris Frith．心智的构建—脑如何创造我们的精神世界[M]．杨南昌译．上海：华东师范大学出版社，2012．

Experimental Study on Teaching Method of Pythagorean Theorem

WU Zeng-sheng1, ZHENG Yan-hong2, LI Hong-yan2, CHEN Ya-fen2
(1. Xianju Teaching Research Office, Zhejiang Taizhou 317300, China; 2. Anzhou Middle School, Zhejiang Taizhou 317300, China)

The Pythagorean theorem is an important theorem in mathematics, in the teaching, we should strive to enable students to engage in activities of refinding the theorem aturally and reasonably, to infiltrate the mathematical culture. Through the following two tasks to guide students to carry out research activities: (1) to cut spell a big square with the same size of two square piece of paper; (2) to cut spell a big square with different sizes of two square piece of paper. let the students complete the task (2) by analogy of task (1), to find the Pythagorean theorem naturally in the process of solving the problem. to design the following teaching experiment research scheme: comparing this teaching method and use method that Pythagoras found the theorem in legend. The results show that the new teaching method has a stronger sense of discovery, and it has better effect to find the memory of the discovery process.

Pythagorean theorem; teaching experiment; found again

G632.0

A

1004–9894（2017）01–0050–05

[责任编校：周学智]

2016–08–21

浙江省2014年教育科学规划课题——基于脑、适于脑和发展脑的数学教学实践研究（2014SC295）

吴增生（1962—），男，浙江仙居人，浙江省特级教师，教育部国培专家库成员，浙江师范大学教育硕士实践导师，主要从事中学数学教育研究．