基于初中九年级数学学业水平监测结果的分析与启示——以吉林省C市为例

王 宏，史宁中，李淑文

（东北师范大学 教育学部，吉林 长春 130024）

基于初中九年级数学学业水平监测结果的分析与启示
——以吉林省C市为例

王 宏，史宁中，李淑文

（东北师范大学 教育学部，吉林 长春 130024）

为了全面、客观、真实地了解和把握中小学教育的质量，为教育决策提供信息、依据和建议，吉林省某市对初中九年级数学学业水平进行了测试．测试结果表明，该市初中九年级数学学业整体水平良好，但在知识技能、数学思考和问题解决等方面还存在一些问题．因此，在中学数学教学中，要提高学生“理解”维度的认知水平，重视“数学思考”目标的实现，充分认识“综合与实践”的价值．

学业水平；监测；分析；启示

1 研究背景

近年来，一些国际组织和发达国家积极推进的学生学业成就调查项目，如IEA的TIMSS项目、OECD的PISA项目和日本的学力调查等都已形成独立的学业成就测评体系，在促进区域或本国教育质量提高方面发挥了独特的作用．为了全面、客观、真实地了解和把握中国中小学教育的质量，准确地向国家报告基础教育质量的现状，为教育决策提供信息、依据和建议，2007年11月30日，中国教育部基础教育质量监测中心成立，并从2007—2016年，先后在中国部分省和直辖市的样本县（市、区）开展了试点监测，并根据监测结果，分别向教育部、各监测样本省、样本县区提供了各类监测结果报告．

在此背景下，2015年9月，吉林省C市在国家基础教育质量监测工作经验的基础上，以《教育部关于推进中小学教育质量综合评价改革的意见》中五大领域的20项指标为测试框架[1]，围绕品德发展水平、身心发展水平、兴趣特长养成和学业负担状况4个领域设计了调查问卷，在学业发展水平方面以小学语文、数学、音乐；初中语文、数学、英语、科学；高中语文、数学为测试科目，系统地评价了该市中小学的教育质量．这里将就该市初中九年级数学学业水平的测试结果进行分析，并尝试提出一些具有普遍意义的启示和对策．

2 研究的过程

2.1 测试目的和对象

该次初中九年级学业水平测试的目的是：了解该市初中九年级学生在数学知识技能、数学思考和问题解决等方面的学习情况、不同区县数学教育水平的差异，为该市义务教育阶段初中数学课程改革的决策、教育质量的提高、数学教学与评价的改进提供数据支持．

测试对象为该市234所初中、52 720名九年级学生．

2.2 测试试卷的编制

为了了解学生在知识技能、数学思考和问题解决等方面的学习情况，试卷以《义务教育数学课程标准（2011版）》中规定的学段目标和内容为依据[2]，以考查初中九年级学生数学学科核心素养为导向，综合了不同版本初中九年级数学教科书的共同内容．将测试框架分为内容领域（数与代数、图形与几何、统计与概率）和认知维度（了解、理解、掌握、运用）两个方面．

命题经历了制定测试方案、编制测试框架与命题指南及细目表、征集题目、专家访谈、预测、试题修改、组卷、研制评分标准等过程，并明晰每一题目所考察的内容和认知水平．

试卷的分值为120分，考试时间为90分钟．试卷包括22道题，其中选择题有10个小题（每小题3分、共30分），填空题有6个小题（每小题4分、共24分），解答题有6道题（共66分）．试卷的难度系数为0.71，区分度为0.59，符合该次测试的性质和目标．

3 研究结果与分析

3.1 宏观统计结果分析

根据这次学业水平测试的目的，运用SPSS统计软件，对每道题从知识领域（数与代数、图形与几何、统计与概率）和认知维度（了解、理解、掌握、运用）两个方面分别对学生的答题正确率进行了统计，其结果如图1、2．

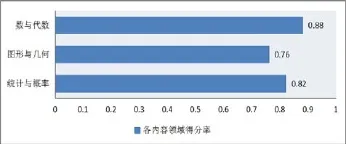
图1 初中九年级数学各内容领域的得分率

从图1可知，学生在数与代数方面表现最好，得分率为88%，在统计与概率方面表现得一般，得分率为82%，而在图形与几何方面表现最差，得分率为76%．从图2可知，学生在了解水平上的表现最好，得分率为91%，而在理解和运用水平上的表现较差，得分率为73%和75%．

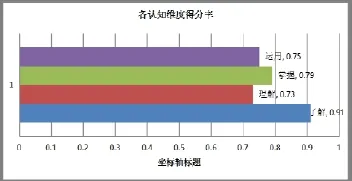
图2 初中九级数学各认知维度的得分率

测试结果表明，大部分学生具有扎实的基础知识和基本技能，具有较强的解决常规问题的能力．但学生在有关概念的理解、数学思考以及综合运用所学知识解决问题的能力等方面相对薄弱，下面结合一些得分率较低的试题进行分析．

3.2 具体问题分析

3.2.1 数学知识与技能

选择题（6）：小明抛一枚质地均匀的硬币，连续抛 3次，硬币落地均正面朝上，如果他第四次抛硬币，那么硬币正面朝上的概率（ ）．

（A）大于反面朝上的概率

（B）小于反面面朝上的概率

（C）等于反面朝上的概率

（D）不确定

该题考查的内容领域是统计与概率、认知维度是理解．主要考查学生是否理解概率含义，得分率为72%，区分度为 0.65．很多学生选择了“A”，失分的主要原因是缺乏随机观念，认为发生过的结果比没有发生的结果更容易出现，从而出错．

该题考查的内容领域是数与代数、认知维度是理解．该题是一道开放题，答案不固定，学生不用死记硬背、机械模仿，写出一个符合题意的数即可，目的是考查学生对反比例函数及其图像性质的理解和把握，但学生的通过率只有70.06%．从学生的答题情况看，一是有些学生对这样的题型感到陌生，不知道填什么；二是有些学生没有很好地理解反比例函数图像性质，只是机械的记忆．

3.2.2 数学思考

填空题（16）：小亮从家步行到公交车站台，等公交车去学校．图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系．则公交车的速度是__km/min．

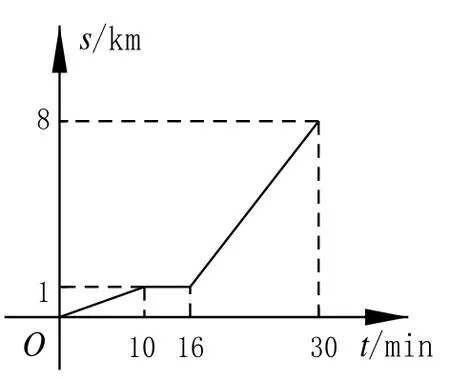
（第16题）

该题是一道用图像表示时间和路程对应关系的函数题，根据图像可知小亮在不同时刻所走的路程．解题需要学生认真观察图形的特点，发掘图中隐含的条件，充分利用图形的性质或几何意义，把“形”正确表示成“数”或“代数式”的形式，进行分析计算．但从学生答题的情况看，多数学生不会将抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来进行数学思考，对“以形助数”或“以数解形”，将复杂问题简单化、抽象问题具体化的思考方法感悟不深，运用不熟．

解答题（20）：如右图，正方形每条边上放置相同数目的小球，设一条边上的小球数为x，请回答下列问题：

第 20（1）题

（1）A、B、C三位同学分别用下面3个代数学式表示正方形边上的所有小球数，你认为他们列出的代数式对吗？请说明他们是怎样思考的．

（2）如右图，将正方形改为立方体，每条边上同样放置相同数目的小球，设一条边上的小球数为x，请用含有x的代数式表示立方体上的所有小球数．

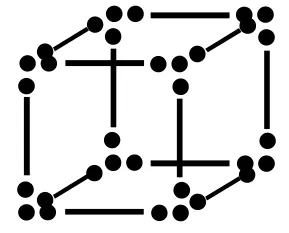
第 20（2）题

该题主要考查学生运用字母表示数、数量关系和变化规律的符号意识，以及运用数学语言清晰、正确的表达能力，但学生的通过率并不高，问（1）的通过率是68.06%，问（2）的通过率是 69.01%．从学生答题的情况看，一些学生不能将数学文字语言、符号语言和图形语言进行正确转换，说明学生的符号意识和数学表达能力还需提高．

3.2.3 数学问题解决

该次测试中，解答题的第17题是列方程解决实际问题，学生回答得较好，第（1）问学生的通过率是84.58%，第（2）问学生的通过率85.01%．第18题是运用“统计与概率”的知识和技能解决实际问题，学生需要根据已知的条形统计图和扇形统计图中给出的信息，算出参加报社调查的出租车司机数，然后补全条形统计图，计算出扇形统计图中的“m”．但学生的通过率并不高，只有70%左右，说明学生利用几何直观信息解决统计问题的能力不足．具体问题如下：

解答题（18）．（本题10分）为更好地宣传“开车不喝酒，喝酒不开车”的驾理念，长春市一家报社设计了如下的调查问卷（单选）．在随机调查了长春市部分出租车司机后，统计整理并制作了统计图：

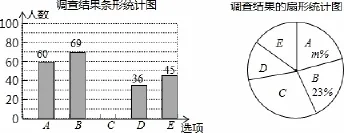
根据以上信息解答下列问题：

（1）补全条形统计图，并计算扇形统计图中m=_____；

（2）若长春市有 15 000名出租车司机，请你估计支持选项B的司机大约有多少人？

4 教学启示

4.1 提高学生“理解”维度的认知水平

“理解”是数学学习中非常重要的一个认知维度，是“掌握”和“运用”的基础，学生只有对基本数学概念、原理和法则的深度理解，才能有“掌握”和“运用”认知水平的提高．但从上面的分析来看，学生在“理解”维度上的平均得分率最低，明显低于“了解”水平．形成这种现象的原因可能是：（1）有些教师对一些基本数学概念、原理和法则，只是抽象的讲解、死记硬背和机械训练；（2）一些教师忽视“理解”水平，追求更高难度和水平试题的训练．

在《义务教育数学课程标准（2011版）》中，有很多知识点被定义为“理解”水平，例如，平行四边形概念的要求，由原来的掌握变成了理解；矩形、菱形和四边形的概念，由原来的掌握变成了理解；平行四边形、矩形、棱形和正方形之间的关系，由原来的了解变为理解[3]．

因此，教师要重视理解水平的教学，要从学生的认知规律出发，从数学概念、原理产生的背景入手，以丰富的典型事例为载体，让学生通过观察、分析、归纳、抽象和概括等思维活动，形成数学概念、发现数学原理和法则，感悟其蕴含的数学思想，从而加深对数学概念、原理和法则理解的深度和广度．

4.2 重视“数学思考”目标的实现

该次测试不仅考查了学生对数学课程内容的理解和掌握程度，还关注了学生在数学思考方面的表现．从测试结果看，学生在“数学思考”方面的表现并不乐观，表现为一些学生不会运用代数式、方程、不等式、函数等表述数量关系；不会用数学语言、符号和图表等说明和解释数学思考过程、数学结论的合理性；不会将抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来进行数学思考．

数学思考是指以数学语言、符号、图形为载体和原料的思维活动过程，其目标的实现离不开学生的数学活动（包括实际操作活动和思维活动）．因此，在数学教学中，教师要精心设计一些给学生带来理智挑战、认知冲突和精神享受的数学活动，给学生更多思维训练的时间和空间，让学生在动手实践、自主探究和合作交流中学会思考和想象、学会表达和说明，学会解决问题、应对困难的思考方法，进而积累数学活动经验，感悟数学思想，提高数学素质．

4.3 充分认识“综合与实践”的价值

《义务教育数学课程标准（2011版）》为了实现“积累数学活动经验，培养学生应用意识和创新意识”的数学课程目标，划分了一个“综合与实践”领域，并给出了具体的实施建议[2]．然而，新课程实施以来，由于考试压力大、教学时间紧，教师的自身知识或能力不足，找不到好课题等原因，相当多的学校和老师并没有充分认识到“综合与实践”的价值，忽视了“综合与实践”的教学．特别是在“综合”方面，教师更关注的是数学内部知识的联系和综合，而对数学与其它学科、数学与生活实际的联系，虽有涉及，但比例较小，重视不够．

其实，学生经历将其它学科问题和实际生活问题“数学化”的过程，可以激发学生运用知识解决问题的相关潜能，提高学生的数学应用意识．因此，要注重数学与生活实际、数学与其它学科的联系和应用，使学生认识到数学在社会生活和其它学科中的作用，培养学生运用数学知识和方法的态度，学会运用数学解决实际问题的思想方法，提高学生的数学应用意识和创新意识．

[1]中华人民共和国教育部．教育部关于推进中小学教育质量综合评价改革的意见[Z]．

[2]中华人民共和国教育部．全日制义务教育数学课程标准（实验稿）[M]．北京：北京师范大学出版社，2001．

[3]綦春霞．初中图形与几何及教学案例分析[M]．北京：北京师范大学出版社，2015．

Analysis and Inspiration of the Academic Level Monitoring Results in Ninth Grade Middle School in Mathematics——Take C City in Jilin Province as an Example Abstract

WANG Hong, SHI Ning-zhong, LI Shu-wen
(Faculty of Education, Northeast Normal University, Jilin Changchun 130024, China)

In order to understand and grasp the educational quality of primary and secondary schools comprehensively, objectively and truly, and also to provide information, basis and advice for education decision, a city of L Jilin province test the academic level of the ninth grade middle school in mathematics. The results of the test shows that the mathematics academic level of the ninth grade middle school in the city is fine. However, there are still some problems in the aspects of knowledge and skills, mathematical thinking and problem solving. Therefore, in the middle school mathematics teaching, we should improve the level of students’ cognitive level in the “understanding” dimension, attach importance to achieving the goal of “mathematics thinking” and also fully recognize the value of “synthesis and practice”.

academic level; monitoring; analysis; inspiration

G632.0

A

1004–9894（2017）01–0047–03

[责任编校：周学智]

2016–11–21

北京师范大学中国基础教育质量监测协同创新中心自主课题——国家义务教育质量监测等值方案研究（2016-03-004-BZK01）；吉林省高等教育教学改革研究课题——中学数学卓越教师的学科知识特征与培养模式研究；东北师范大学全日制教育硕士综合改革项目（JSGG14001）

王宏（1968—），男，黑龙江五常人，东北师范大学博士生，北京师范大学附属实验中学教师，主要从事数学教育教学研究．