信息技术对促进数学基本思想教育的价值分析

刘咏梅，吴立宝

（1．江西师范大学 数信学院，江西 南昌 330022；2．天津师范大学 教师教育学院，天津 300387）

信息技术对促进数学基本思想教育的价值分析

刘咏梅1，吴立宝2

（1．江西师范大学 数信学院，江西 南昌 330022；2．天津师范大学 教师教育学院，天津 300387）

信息技术融入数学教育有利于展现抽象思维的理性文化特点，提升对数学对象关联性的理解；有利于增强归纳推理的客观性和演绎推理的深刻性；有利于为建模和利用模型解决问题提供丰富素材；有利于将数学思想的文化背景、数学思想的关联性和数学思想与数学知识的联系有效展现于课堂，突出基本数学思想的产生、发展和应用．

数学基本思想；信息技术；数学教育

信息技术是指利用计算机、网络等各种硬件设备及软件工具与科学方法，对文图声像各种信息进行获取、加工、储存、传输与使用的技术之和[1]．信息技术的发展是教育发展的重要内涵和源泉，推进教育信息化已成为各国抢占教育发展的制高点[2]．教育实践中，越来越多的教师意识到信息技术给数学教育带来的巨大影响，但还存在“信息技术影响教育方式还是影响教育本质”的争论，部分教师一直徘徊在“用与不用”的边沿，还有部分教师使用信息技术一般停留在“利用丰富的动态效果，提升学生学习的兴趣；利用信息技术缩短一些活动的时间，用信息技术代替人的实验；展示学生或教师的操作过程；展示例题、习题等解题过程”等一些辅助教学的层面上．

对技术作用于教育的过程与效果的认识是信息技术融入教学的关键[3]．数学思想是数学素养的基本内涵，也是数学教育的基本目标，如果信息技术的融入不能对这一目标的实现具有较大的促进作用，其价值就大打折扣．因而，探索信息技术与数学思想的联系，是解决信息技术融入数学教育的基本问题．数学基本思想具有隐性的特点，信息技术具有直观性和动态性，两者互为补充，从根本上确定了建立联系的可能性．抽象、推理和建模思想是基本的数学思想[4]，也是数学的基本特点“高度的抽象性、严密的逻辑性和广泛的应用性”在思想方法上的体现．

1 信息技术凸显抽象的价值

抽象是数学的本质属性，也是认识事物的一般思想[5]．人获得知识所凭借的是先天的，同时又依赖于经验的“直观能力”，数学抽象能力与这种直观能力是同构的[6]．数学抽象是对客观事物量的抽象．量是指事物存在的规模、方式以及发展的程度、速度．信息技术的融入可以使数学教育突显数学的发生、发展过程，展现抽象思维的理性文化特点和数学对象的相互关联性．

1.1 展现抽象思维的理性文化特点

数学是人类抽象思维的创造，是文化的重要组成部分．齐民友先生在《数学与文化》中指出“一个没有现代数学的文化是注定要衰弱的．”[7]信息技术起源于对大数据的分析和处理，强调对事物的定量分析，数字化、全球化、交互性、开放性是信息技术文化的基本特点．这些特点都凸显着信息技术文化的理性内涵，这与数学文化是相通的，文化背景的共性是数学教育与信息技术相融的重要条件，也是展现抽象思维理性文化的有利因素．

1.1.1 体现抽象思维的继承性

文化的基本属性是传承性，数学思想是数学文化传承的基本元素，信息技术的运用可以更好地展示前人对数学问题的思考，启发当下学生．数学教材中有一些内容是经历长期发展的，历史上人们的研究过程，对今天学习面临的问题具有启发性，这些内容体现了数学的继承性，也体现了信息技术运用的重要性．数学史主要是数和形两大基本概念的产生、发展、变迁的历史[8]．历史上对无穷问题的思考往往也是借助数与形的转换进行的，信息技术的展示可以使学生更好的认识无穷问题．如由于中学生对无穷的认识和理解处于初级阶段，对是等于1还是小于1的问题，学生理解会有一定的困难．教学中，借助两个长期被运用的基本几何图形面积的特点（图1，图2），不仅可以帮助学生理解问题，而且可以通过借鉴历史的思想，帮助学生对问题进一步的抽象，从而认识和解决问题．

图1 对正方形的分割(1)

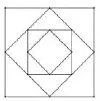
图2 对正方形的分割(2)

1.1.2 体现抽象思维的审美性

数学教学在抽象思想的形成过程中，还应使学生全面理解数学，培养学生对数学美的鉴赏能力和对真、善、美的追求．史宁中指出：认为数学是一门创造性的、受审美因素支配的学科，比认为数学是一门别的、特别是经验的学科要更确切一些[4]．学生学数学的过程，本质上就是感受数学、领悟数学、欣赏数学、从事再创造的过程[5]．数学美表现在数学本质上，表现在数学思想、精神上[9]．数学美的鉴赏体现在对数学内涵的理解之中，信息技术运用于数学抽象思想教学，应由提升兴趣过渡到传承文化，追求数学美的本质．数学研究基本特点是揭示对象本质内涵，用直观的方式展示对象的本质是信息技术的重要运用．如三角函数的本质是周期性，其重要性也体现在周期性上，同一周期的不同函数具有的特点用信息技术呈现，不仅能加深学生的理解，而且给学生美的体验．如图 3在同一坐标系中画出，的函数图形，学生不仅能够理解3者之间的关系，还能形成一种和谐之美．借助动画还能形成波浪的美丽画卷，对培养学生美的鉴赏能力具有积极才的意义．再如教学勾股定理时可以借助信息技术展示赵爽弦图、欧几里得的证明图、勾股定理的迭代图等，学生通过比较各种证明方式，体会不同文化对美的追求和理解．

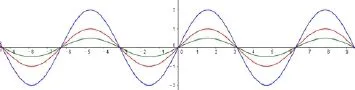
图3 3个正弦函数图象

1.2 提升对数学对象关联性的理解

理解是对对象本质的认识，也是内在概念网络的建构，数学知识相互关联性决定了借助知识的联系形成新的知识是理解的重要环节，也是解决问题的基本依据[10]．数学抽象的特殊性使对抽象对象关联性的理解成为教育的重点和难点．信息技术的运用可以使学生借助大量的、多角度的信息建立知识之间的联系，从而获得解决问题的途径．

1.2.1 由表及里深化理解

知识之间的差异性体现了认识的发展性．借助信息技术的运用，展示发展的特点，是学生深化理解的重要途径．如当实数和复数的乘法运算学生都掌握后，引导学生思考实数与实数相乘和复数与复数相乘差异产生的本质、几何表示的特点、二维空间与一维空间的属性等问题．学生可以借助信息技术发现两者在“形”上的区别和联系，从而更好地思考理解算法的一致性，认识知识的联系和发展性．

1.2.2 借助图形探索问题解决的方向

数学作为文化的一部分，其最根本的特征是它表达了一种探索精神[7]．这种探索精神的重要体现是数学研究不断思考问题解决的依据，寻找问题解决的方向．教师借助信息技术提供问题解决的正反方两方面的信息，学生在不断辨析中获得理解，并发现问题解决的途径．如在学习两角和的余弦公式时，动态演示及变化时及的几何变化特点，学生可以发现它们之间是相互关联的但又不是简单的“去括号”的关系．进一步在学生探索的变化与的变化关联性后，寻找这一关系的数学表达，从几何意义上把表示出来就成为关键，于是作出就水到渠成了．

2 信息技术凸显归纳与演绎的关系

推理是由一个或几个已知的前提，推导出结论的思维过程．归纳推理和演绎推理相互依赖，形成不可分割的整体．传统数学教学更强调演绎推理，信息技术的融入使数学实验日益受到关注，通过问题的动态表现，学生有了更多的观察和归纳的机会，对形成猜想，获得顿悟都有积极的意义，在此基础上，借助逻辑推理检验猜想，形成归纳推理、演绎推理共同构成的推理链，使学生经历推理的全过程，对推理客观的依赖性、相互之间的依赖性有更好的理解．

2.1 归纳推理的客观性

归纳推理是从个别前提出发，经过观察和经验的分析得出一般结论的过程．数学知识是客观存在的，数学教育应该使学生的学习基础建立在客观事物认识之上．借助信息技术展示客观事物的特点，能使学生形成的归纳猜想更可靠．

2.1.1 依赖客观现象认识规律

信息技术能模拟动态的或平常无法观察到的现象[11]，使学生的学习更多地依赖客观．数学是一门抽象的科学，对其抽象过程，徐利治教授指出：一般说来，数学抽象共有4个步骤，即观察实例、抓住共性、提出概念、构筑系统或框架（理论）[12]．信息技术的动态效果，使学生能够经历 4个完整的步骤，将解决问题主要依赖主观思考，转变为主观思考和客观验证相统一的过程．如以下问题的思考．

这一问题的分析可以借助动态演示，观察图形的变化过程，归纳出图4是由一种极端到另一种极端的两种情况，从而得出m的取值范围的直观结论．

图4 圆及其两条切线

2.1.2 依赖图形确定论证方向

在数学教学中，利用信息技术有利于培养学生探索的意识，形成利用信息发现问题的能力，引导学生关注问题的产生原因，并依赖经验探索解决问题的途径．如已知a,b为非负数，，求M的最值．利用信息技术的作图工具可以作出的草图，提出最值存在的猜想，这为问题的解决确定了方向．分析作图过程，进一步探索最值产生的原因．只由难以确定M的最值情况，M的最值决定因素是这一条件．依据以往的经验，和的最值一般是在两数相等或一些极端情况的时候获得．于是可以得到猜想：当时，M有最小值；当a,b有一个为0时，M有最大值1．借助信息技术进行验证使这一猜想更为可靠，在此基础上的证明便可以根据猜想依据的相关不等式寻找思路．

2.2 增强演绎推理的深刻性

信息技术有效运用于数学教学，应着眼于对学生数学思维品质的培养，尤其是数学思维深刻性的培养[13]．数学对象的表现形式是多样的，借助信息技术演示变化过程，能够提升对变化中不变的认识，及对思维对象本质的完整把握和认识．在此基础上形成严密的论证能揭示研究对象的本质，体现推理的深刻性．

2.2.1 揭示研究对象的本质

要全面认识数学对象，揭示研究对象的本质，离不开直觉思维．徐利治说：直觉是对数学真正理解的重要途径，直觉能使相应的内容在头脑中真正成为“非常直接浅显的”和“非常透彻明白的”，从而真正达到“真懂”或“彻悟”的境界．信息技术的使用有利于形成直觉思维．如函数的图象是“双勾”，通过旋转坐标系进一步猜想图形可能是双曲线，由此便把握了对象的本质特点，在此认识基础上的论证可以将函数表达式转化为双曲线的标准方程．

2.2.2 宏观把握研究对象

借助信息技术可以从宏观上把握研究对象．如探究圆锥曲线的关系，可以借助几何画板等软件动态演示三类圆锥曲线之间的关系，形成对圆锥曲线的动态认识和统一定义的理解，为演绎论证提供整体的思路和方向．借助信息技术，对一些数学问题也可以整体把握其特点，如以下问题．

图5 函数图象(1)

图6 函数图象(2)

从图象分析可以得出一般结论：两种不同情况实质上是x轴上下平移的结果，而且随着常数的改变，x轴可以任意上下移动，但无论怎样移动，函数图象的关系不会改变，两函数图象交点所对应的x的值不会改变．由此便能够较为宏观的把握对象，为深化研究提供基础．

2.3 增强数学学习中归纳与演绎的不可分割性

数学化是人类文明进步的产物，是人类发现活动在数学领域里的具体体现．所谓数学化就是由现实问题到数学问题，由具体问题到抽象概念的认识转化[14]．归纳推理和演绎推理是数学化的重要组成部分，两者互为补充，共同将实际问题转化为数学问题，并形成数学的结论．信息技术融入数学课堂，使数学课堂的信息更加丰富，便于学生多视角的收集信息．信息技术融入数学课堂，也可以使抽象的问题具体化，便于学生认知的转化．

2.3.1 由现实问题归纳出数学对象的性质

信息技术的融入可以将丰富的现实资源展现在数学课堂．教师不仅需要对信息进行选择，而且需要引导学生收集信息，将现实问题转化为数学问题，提升学生的信息素养，体验发现问题、提出问题、分析和解决问题的过程，使学生获得具有生命力的数学知识．

精确的定义是逻辑推理的基础，数学对象性质研究和论证往往是从定义出发的．实际上数学对象很多重要的本质属性的抽象都依据客观原型．借助信息技术使学生体验由实际对象提炼数学模型性质的过程，对学生形成正确的认知具有重要意义，特别是一些具有逻辑起点的概念的性质．如向量的概念是介于几何与代数之间的概念，又是学生需要综合考虑两个属性的概念，因而这一概念是数学教学的重要内容．在向量运算性质的教学中，可以借助视频、截图等，在现实情境中体会大小和方向在客观对象中的意义，体验加法等运算性质的现实依据．

2.3.2 关注具体现象到一般结论的推理

任何数学问题研究都是从具体到一般的探索，教学中需要关注具体问题到一般问题的转化．如函数的教学，《高中数学课程标准》明确指出：“学会运用函数图象理解和研究函数性质．”教师在教授函数的奇偶性、单调性等性质时，借助信息技术的融入，将画图和研究图作为重要的教学内容，并对特殊的函数进行研究，使学生很好地理解任意、增减、对称等概念，这对学生形成函数性质的理解和认识是不可或缺的环节．正如李大永、白永潇、张思明等老师在对北京大学附中辛华老师的函数单调性教学点评中指出的：华罗庚先生提出的“以退求进”的学习策略“先足够地退到我们所容易看清楚的地方，认透了，钻深了，然后再上去”[15]，易使学生理解概念的产生、发展和解决过程．

3 信息技术为建模与用模提供丰富素材

数学并非是对客观事物或现象的直接研究，而是借助定义和推理进行的逻辑建构[16]，最终表现为模式化．模型建立的情况决定了问题解决的情况．信息是客观世界中各种事物的运动状态和变化的反映，表现的是客观事物运动状态和变化的实质内容[17]．依据信息的认识和理解，可以得出客观实际、信息与数学之间的关系（如图7）．由图7可以看出，数学模型是从实际问题中通过提取信息并进行模型化而成的．没有信息技术的支持，课堂主要由教师的表达来传递信息，教师的语言、文字和绘图等表现能力决定了课堂信息的状况，成为模型建构局限性的影响因素．信息技术使得学习空间具有开放性的特点，是一个生态系统．教师多角度、多层次将信息引入课堂，形成课堂教学的动力源，为学生构建数学模型提供依据．信息技术的融入可以为学生学习数学知识和解决问题提供丰富的背景，可以将模型建构、模型运用等思想凸显于数学课堂．

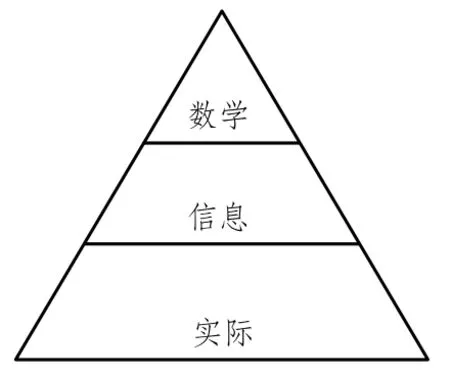
图7 客观实际、信息与数学之间的关系

3.1 突出实际原型对模型的影响

数学结论的正确性取决于基本方法，也就是公理化方法．公理化的起源是公理，公理的形成是实践提供的信息的整理，因而，数学研究建立在信息收集和整理之上．学生的学习首先要学会信息的收集和整理，从实际原型中提炼出数学模型，再对模型进行分析，形成一般的认知．“所谓数学模型，指的是对现实原型为了某种目的而作抽象、简化的数学结构．”[18]信息技术融入数学教育能够获得更多的现实原型，为学生的模型建构提供大量的素材．

3.1.1 体验客观现实在模型建构中的作用

“格物致知”是我国清代颜元最早提出的，数学建模学习也不例外，在信息技术的环境下，需要经历信息的收集、加工等“格”的过程才能达到“知”的目的．模型的建构过程是感性思维到理性思维的认识过程，是从信息中抽取一类对象的本质属性，形成对对象的抽象认识，并用数学语言将认识固定．

数学产生于问题，而问题的提出离不开语言描述，问题的解决又需要建立数学模型，最后才能形成结论，数学教学需要展示这个完整的过程[19]．在概念的形成教学中，借助信息技术的帮助，学生可以更好地理解概念的建构过程．如倾斜角的概念是高中数学的重要概念，这一概念的教学应该突出产生、形成和理解3个重要环节．可以通过多媒体演示生活中的不同倾斜状况引起对象性质和特点的不同状况，构建对倾斜问题的感性认识；接着经过抽象、建立坐标将实际问题转化为直角坐标系中直线与水平坐标轴之间夹角的问题，构建数学模型；在形成概念过程中，引导学生在4个交角中合理选择一个作为倾斜角，并描述倾斜角的特点；在概念理解中，用数学思维重新理解和认识实际问题，辨析数学概念并通过建立概念的联系不断完善认知结构．

3.1.2 体验模型的性质运用于客观现实问题的解决

数学特点的重要体现是研究对象的确定[20]．学生在对确定的数学对象进行研究后，获得理性认识，有利于对问题的理解和解决．如研究圆锥曲线过焦点的直线经圆锥曲线反射后直线的特点，教师可以借助多媒体演示一系列灯的反射面（如电影放映机上聚光灯泡的反射镜面、牙科医生用于辅助治疗的灯的反射镜面、探照灯的反射镜面、路灯的反射镜面等），引导学生思考这些灯的反射面的特点，以及与水平面相截的曲线特点，并进一步思考选择怎样形状的灯以及灯泡应该装在什么位置才能适合不同的需要．学生从已有的认识出发，思考实际问题的解决，如电影放音机需要一束平行光、牙医需要聚光、路灯需要照射面积大的光等，不同的需要应该选择不同的圆锥曲线形作为灯的反射面，将实际问题的研究与数学模型的性质研究进行有机的结合，体验运用数学模型性质解决实际问题．

3.2 凸显信息对模型研究的意义

数学教学中对于解决问题的程序过程或探索法（heuristics）的掌握，几乎一定代表着生长[21]．数学上所采取的符号、概念、公式、法则、定理、公理的教学，本质上就是一种信息加工模块的教学[22]．数学学习中，学生需要经历从感性认识到理性认识的升华过程．这一过程是探索的过程，也是数学概括的过程，需要丰富的信息作为基础．3.2.1 依据多角度信息认识规律

信息技术的融入可以扩大课堂信息的容量，学生的学习可以在大量案例中探索规律，形成概括的结论．如以下数列中的典型问题的教学．

3.2.2 依据特殊化发现规律

数学是研究事物一般性质的科学，但研究过程往往需要将问题特殊化为若干具体问题．借助信息技术可以使特殊化的信息更加丰富，从中抽象出一般规律．如由余弦定理到勾股定理、由指数函数研究到的研究等，都是将问题特殊化寻找一般规律，再在一般意义上进行证明．

借助信息技术可以对特殊情况的大量信息进行分析，如探索直线与平面垂直的判定定理，借助动画演示，对与平面内一条直线垂直、两条直线（各种位置）垂直的情况进行分析，从而得出一般猜想．

4 思考与建议

上述以抽象、推理及模型3种数学思想为例，结合案例分析了信息技术融入数学教育对学生数学思想的形成的价值．数学可以被教得更好，让学生兴趣盎然，也可以被教得更坏，让学生望而生畏[23]，重要的是看教师怎样提供信息，怎样引导学生加工信息．“如何发挥用巨大投入建设起来的信息化设施的作用，提高教育教学的实际效果，应当是我们着重探索的问题．”[24]纵观数学教育史，世界各国的数学教育目的大致始终徘徊于技术和科学两者之间，前者关注数学教育的实用性，后者关注数学教育的素质性．只有两者辩证地结合，才能正确把握数学教育的基调[25]．数学思想具有科学和技术的共同的属性，数学思想教学不仅为信息技术融入数学教育提供了切入点，而且是科学与技术结合的重要途径．教师需要具备整合技术的学科教学知识[26]，需要在对教材全面理解的基础上深入挖掘信息技术的功能，努力发挥其在提升数学素养方面的作用．将数学思想的文化背景、数学思想的关联性和数学思想与数学知识的联系有效展现于课堂，突出基本数学思想的产生、发展和运用教学，才能充分发挥信息技术融入数学课堂的价值．

4.1 展现数学抽象思想的文化背景

数学思想是数学抽象的产物，无论如何抽象的数学对象都是基于相对具体的事物本体，有其产生的文化背景．文化是人类的思维方式和行为方式[27]，数学文化是一种精神，这种精神来源于理性的思维方式和观念形成的力量[28]．在教学中，教师要对教学内容的文化特点和抽象的意义有全面的认识和理解，并借助信息技术的融入，呈现数学基本思想的产生背景．

如函数概念的教学在中学经历了两个重要的阶段，给出了“变量说”、“对应说”两个定义．为什么函数要介绍两个定义、为什么用函数思想贯穿基础教育数学课程的观点得到广泛认可？教师应对函数所包含的文化因素进行分析，才能引导学生更好地理解这些问题．世界万物共同的本质属性是运动和变化，函数以运动变化为研究对象，用模型的方式对客观现实共同本质属性进行探索，是数学与世界联系的重要桥梁，运动变化也成为函数概念产生基础．但是数学文化的特点决定了数学研究不能停留在事物的直观认识，因而需要在运动变化中揭示“变中不变”的规律，并用“数”进行描述，形成数集之间的关系，这也是对函数概念的进一步抽象．对函数的认识是人类思维方式和行为方式的体现，也就是人类的文化特点在数学中的重要体现．教师应基于对函数发展的认识，借助信息技术，展示从自然界运动变化到数集对应的抽象过程．

4.2 展现数学思想之间的关联性

数学基本思想是相互联系的，在教学中应突出其关联性．如归纳是建立在一定的逻辑之上的，即每个归纳的结果都隐含着许多复杂三段论式的逻辑推理，每一个演绎推理又是基于一定的猜想，学生的归纳推理能力与演绎推理能力应协调发展，教师在教学中应将两种推理模式进行有机结合．

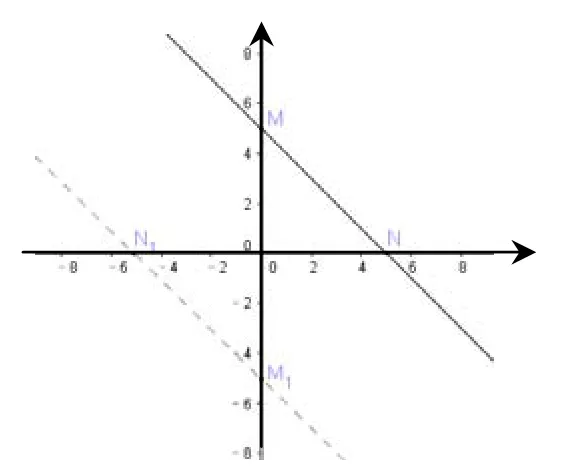
图8 关于原点对称的两条直线

4.3 展现数学知识对数学思想的基础性

数学基本思想蕴含于数学问题解决过程中，是现实问题抽象而成的，数学问题解决不仅能形成数学结论，而且渗透着数学基本思想，数学结论又为形成数学基本思想奠定了新的基础．数学的形式化特点使知识中蕴含的数学思想不能完全显现，教师应引导学生借助知识的关联性理解数学思想的关联性．

如函数和数列是两个重要的数学模型．学生虽然能够体会数列是函数的特殊情况，但对两者数学思想的内在联系的认识还难以全面．教师应引导学生在掌握数列和函数基本知识的基础上，理解函数的研究需要特殊化为数列，数列的结论需要依据函数的本质才能加深认识．如引导学生发现函数研究需要借助图形，画图需要描点，描点需要列表，列表的本质就是用表格的方式展示自变量的取值对应的数列与因变量的结果对应的数列之间的关系，也就是将函数特殊化为数列进行分析．再如教学等差数列求和公式时，引导学生探索等差数列的求和可以转化为相同数的加法，进而转化为乘法，从而由等差数列的通项公式转化为求和公式后次数的变化就好理解了．对模型关系的认识是一个由知识到思想，又由思想到知识的辩证发展过程．信息技术的融入，可以将这一过程直观化，使学生不但理解了各个模型的特点，还进一步抽象出模型之间的联系．

数学根植于客观现实世界，是现实世界的高度抽象．推理是数学内部之间的联系，体现着数学间的逻辑性．模型是数学与现实世界之间的桥梁，体现着数学应用的广泛性．教学中应借助信息技术将形式化的数学知识回归实际原型，培养学生现实世界与数学之间双向翻译的能力，展现知识的发生和发展的过程．

改善教学的环境因素是促进学生发展的有效手段，因而要让学生感悟数学基本思想，就需要具有相应的、全面的环境[31]，有效促进学生的思维应当成为判断数学课成功与否的主要标志[32]，信息技术融入数学课堂对改善数学思想教学环境起到了不可替代的作用，使数学思想与数学知识的教学形成整体，互为补充．在课堂教学中，信息技术提供的大量信息，可以使不同的学生采用不同的方式进行学习，也可以使教师灵活地在传统教学与现代教学方法之间切换，形成教学方法的综合运用．另外，信息技术融入数学教育将促进传统教学方式与现代教学方式的融合，形成任何一个都不能 单独拥有的教学力量．

[1]王正义．基于智趣数学的信息技术课堂应用研究[J]．中国电化教育，2014，（12）：126-129．

[2]祝智庭，管珏琪．教育变革中的技术力量[J]．中国电化教育，2014，（1）：6-15．

[3]李彤彤，武法提．技术支撑教育活动系统变革的可能性框架[J]．中国电化教育，2014，（12）：14-18．

[4]史宁中．数学的基本思想[J]．数学通报，2011，50（1）：1-8．

[5]吕林海．数学抽象的思辨[J]．数学教育学报，2001，10（4）：59-62．

[6]史宁中．数学的抽象[J]．东北师大学报（哲学社会科学版），2008，235（5）：169-180．

[7]齐民友．数学与文化[M]．大连：大连理工大学出版社，2008．

[8]黄继蓉，陈光喜，黄韬文．多媒体技术与“数形结合”教学[J]．数学教育学报，2009，18（2）：76-78．

[9]顾沛．数学的美在于数学思想深刻之美[J]．数学教育学报，2011，20（4）：11-17．

[10] 郑毓信，肖柏荣，熊萍．数学思维与数学方法论[M]．成都：四川教育出版社，2001.

[11] 张波，钱林．计算机与数学教学整合中的几个特殊关系[J]．数学教育学报，2002，11（1）：79-82．

[12] 毛京中．高等数学概念教学的一些思考[J]．数学教育学报，2003，12（2）：83-86．

[13] 温建红，涂荣豹．对数学教学中有效运用信息技术的思考[J]．数学教育学报，2008，17（1）：91-94．

[14] 白改平．水平与垂直数学化思想蕴涵的数学教学观及其实施步骤[J]．数学教育学报，2009，18（4）：25-27．

[15] 李大永，白永潇，张思明．高中数学特别教案[M]．福州：福建教育出版社，2012．

[16] 徐利治．数学方法论选讲[M]．武汉：华中理工大学出版社，2000．

[17] 李兴国．信息管理学[M]．北京：高等教育出版社，2011．

[18] 张雄，李得虎．数学方法论与解题研究[M]．北京：高等教育出版社，2003．

[19] 喻平，董林华，魏玉华．数学实验教学：静态数学观与动态数学观的融通[J]．数学教育学报，2015，24（1）：26-28．

[20] 刘咏梅．影响数学观的中学向量概念的教学[J]．数学教育学报，2009，18（4）：9-12．

[21] Nel Nodding．教育哲学[M]．许立新译．北京：北京师范大学出版社，2008．

[22] 方均斌，周文．从信息效应的视野审视数学推理教学[J]．数学教育学报，2013，22（3）：12-17．

[23] 曹一鸣．中国数学课堂教学模式及其发展研究[M]．北京：北京师范大学出版社，2007．

[24] 张景中，彭翕成．深入数学学科的信息技术[J]．数学教育学报，2009，18（5）：1-7．

[25] 张雄，卢锷．论技术·文化·人格三重性数学教育目的[J]．数学教育学报，1995，4（4）：22-25．

[26] 袁智强．整合技术的学科教学知识研究综述[J]．数学教育学报，2012，21（6）：13-18．

[27] 史宁中．漫谈数学的基本思想[J]．数学教育学报，2011，20（4）：1-5．

[28] 刘咏梅，刘军，廖云儿．关于数学文化的几个问题的哲学思考[J]．数学教育学报，2009，18（2）：15-19．

[29] 王申怀．试论数学直觉思维的逻辑性及其培养[J]．数学教育学报，1992，1（1）：66-69．

[30] 徐章韬．面向教学的数学知识：缘起、结构特征、检测及其教育意蕴[J]．课程·教材·教法，2013，33（5）：116-120．

[31] 孙绍荣．教育信息理论[M]．上海：上海教育出版社，2000．

[32] 郑毓信．“数学与思维”之深思[J]．数学教育学报，2015，24（1）：1-5．

Value of Information Technology in Mathematical Thought and Method Education

LIU Yong-mei1, WU Li-bao2
(1. College of Mathematics and Information Science, Jiangxi Normal University, Jiangxi Nanchang 330022, China; 2. College of Teacher Education, Tianjin Normal University, Tianjin 300387, China)

Integration of IT into mathematics education is conducive to show the characteristics of abstract thoughts’ rational culture, to enhance the understanding of the relevance of mathematical objects. IT helps enhance the objectivity of inductive reasoning and profound of deductive reasoning, provides abundant materials for the modeling and solving problems with model. Also IT is beneficial to show the cultural backgrounds of mathematical thoughts, the links of mathematical thoughts and the relevance between mathematical thoughts and mathematical knowledge in classroom, and then highlights the produce, development and application in teaching of basic mathematical thoughts.

mathematical thought; information technology; mathematical education

G424

A

1004–9894（2017）01–0041–06

[责任编校：陈隽]

2016–10–05

江西省高等学校教学改革研究课题——基于卓越型教师的“课堂教学技能实训·数学”课程建设与实践（JXJG-14-2-25）；全国教育科学“十二五”规划 2013年度教育部青年专项课题——内容分布与认知要求双重视角下的义务教育课程标准国际比较研究——以数学课程为例（EHA130395）；天津市教育科学“十三五”规划课题——“幼小”“小初”学段衔接的课程建设实践研究（BE3330）

刘咏梅（1961—），女，河北邯郸人，教授，硕士生导师，主要从事数学教育与数学文化研究．吴立宝为本文通讯作者．