尾翼型EFP形成的数值模拟研究
2017-05-03张孝中赵太勇陈智刚郭光全李建飞
张孝中, 赵太勇, 陈智刚, 郭光全, 李建飞
(1 中北大学地下目标毁伤技术国防重点学科实验室, 太原 030051; 2 晋西工业集团有限责任公司, 太原 030051)
0 引言
随着现代科学技术的发展,尤其是军事科技的发展,使得军事目标的抗打击能力日益加强。应用在末敏弹上的爆炸成型弹丸(EFP),可以用来攻击坦克顶装甲及舰船甲板。为了提高EFP远距离攻击目标的能力,可使用一种尾翼型EFP,使其具有良好的稳定飞行能力。刘建青等[1]对三点起爆形成尾翼EFP进行了实验研究及相关的数值模拟,路鸣等[2]对四点起爆形成带尾翼EFP进行了试验研究,于川等[3]采用了多点起爆方式,对带尾翼翻转爆炸成型弹丸进行了实验研究,Bouet T H等[4]研究了多点起爆方式对尾翼EFP的影响,并得到具有良好尾翼结构和稳定飞行能力的尾翼型EFP。林加剑等人[5-6]使用在药型罩上贴附惰性隔板的方法,对带尾翼EFP形成进行了相关实验研究。Weimann K等[7]就爆炸成型弹丸飞行稳定性进行了实验研究。唐平江等[8]主要研究了壳体对带尾翼EFP成型过程的影响。门建兵等[9]进行了带尾翼EFP形成的三维数值模拟研究。而目前采用在药型罩表面刻槽的方法形成尾翼型EFP的数值模拟研究较少。
文中提出一种在药型罩表面周向对称刻槽,并以45钢填充槽体的结构,用该结构来影响药型罩的塑性变形过程,从而形成一种尾翼型的EFP。对比分析了3种药型罩结构方案,分别对3种方案进行数值模拟,得到了最优方案,继而以该结构方案对尾翼型EFP成型过程的影响进行研究,得到刻槽参数及填充材料对尾翼型EFP侵彻性能和成型效果的影响规律,对今后尾翼型EFP研究工作具有指导意义。
1 计算模型与材料参数
1.1 计算模型
用LS-DYNA软件[10]对刻槽药型罩形成尾翼型EFP过程进行数值模拟,采用Lagrange算法,单位制:cm-g-μs。因聚能装药为轴对称结构,同时在药型罩表面周向对称刻4个槽,故建立1/4模型,以此为例进行数值模拟。整个模型由炸药、填充物和药型罩三部分组成,模型如图1所示,所有单元均为8节点实体单元solid164。计算中采用装药顶端中心点起爆方式。
模型中药型罩的形状为球缺罩,其主要结构参数装药直径为Dk=50 mm,药型罩外曲率半径为R=1.64Dk,壁厚为δ=0.06Dk,装药高度为L=1.2Dk。

图1 计算模型
1.2 材料参数选择
在数值模拟中,药型罩材料为紫铜,本构模型为Johnson-Cook,状态方程为Gruneisen,屈服应力σy表示为:
-(T*)m]
(1)
式中:T*=(T-Tr)/(Tm-Tr),Tm为常态下材料熔化温度,Tr为参考温度(一般为室温)。式中参数值为A=0.09 GPa,B=0.29 GPa,n=0.31,C=0.025,m=1.08,Tm=1 356 K,Tr=293 K。
选择8701炸药,本构模型为HIGH_EXHIGH_EXPL OSIVE_BURN,状态方程为JWL,表达式为:
(2)
式中:P为压力;E为内能。所用参数值为E=10 GPa,A=564 GPa,B=6.801 GPa,R1=4.1,R2=1.3,ω=0.36。填充物材料为45钢。
药型罩和填充物材料参数如表1所示,其中ρ为密度(g/cm3),G为剪切模量(GPa)。炸药材料参数如表2所示,其中D为爆速(m/s),Pcj为爆轰波波阵面压力(GPa)。

表1 药型罩和填充物材料参数[11]

表2 炸药材料参数[12]
2 数值模拟结果及分析
2.1 尾翼型EFP成型原理
由爆轰理论知,炸药爆炸时将产生高温、高压的爆轰产物,爆轰时这些产物将沿炸药表面的法线方向向外飞散。端面具有球缺型凹坑的圆柱状药柱爆炸后,爆轰产物一方面以一定速度沿凹坑表面的法线方向向中心轴线汇聚,形成一股高速度、高密度的气流,即聚能效应;另一方面由于稀疏波的作用,汇聚到中心轴线处的爆轰产物又迅速向周围低压区膨胀,使能量分散开。在成型装药的球缺型凹坑表面放置一个与之相切的金属罩,则爆炸后的爆轰产物将推动罩壁向中心轴线运动,将能量传递给金属罩形成EFP。为了形成一种飞行稳定性较好的尾翼型EFP,需在罩表面周向对称刻槽,并填充材料达到闭气作用。当经过衰减后的冲击波作用于罩刻槽处时,在未刻槽处的罩微元压力比其他位置处大,产生的塑性变形也大,将形成尾翼型EFP。
由于45钢的压缩性比铜小,因此在受到相等爆轰载荷作用时,冲击波压力在钢中衰减比铜快,所以选用45钢填充槽体。
文中提出3种药型罩结构方案:1)无刻槽;2)有刻槽,无填充物;3)有刻槽,有填充物。下文将对EFP成型过程进行数值模拟,将得到较好方案。
2.2 3种方案对EFP形成尾翼的影响
对以上3种方案分别进行数值模拟,取140 μs时结果进行分析。EFP形态见表3,计算结果见表4。

表3 3种方案EFP形态

表4 3种方案EFP速度和长径比
从表3和表4中可知,第一种方案形成的EFP速度及长径比最小,且无尾翼;第二种方案形成的EFP速度及长径比次之,且尾翼形态较差;第三种方案形成的EFP速度及长径比最大,且尾翼张的很开,形态良好,成形效果较好。因此有刻槽、有填充物是较好方案,继续对该方案分析。
当刻槽数目、长度及填充物材料一定时,尾翼型EFP主要受槽宽和槽深等参数影响。下文将对尾翼型EFP成型过程进行数值模拟,并得到两种参数的最优结构设计。
2.3 刻槽深度和宽度对EFP形成尾翼的影响
当刻槽长度L=1.0 cm、宽度W=0.21 cm时,仅改变槽深H,依次取值为0.1 cm、0.13 cm、0.16 cm、0.19 cm、0.22 cm、0.25 cm进行模拟计算。取140 μs时结果进行分析,其计算结果见表5。不同槽深的EFP形态见表6,EFP速度及长径比随槽深的变化曲线如图2所示。
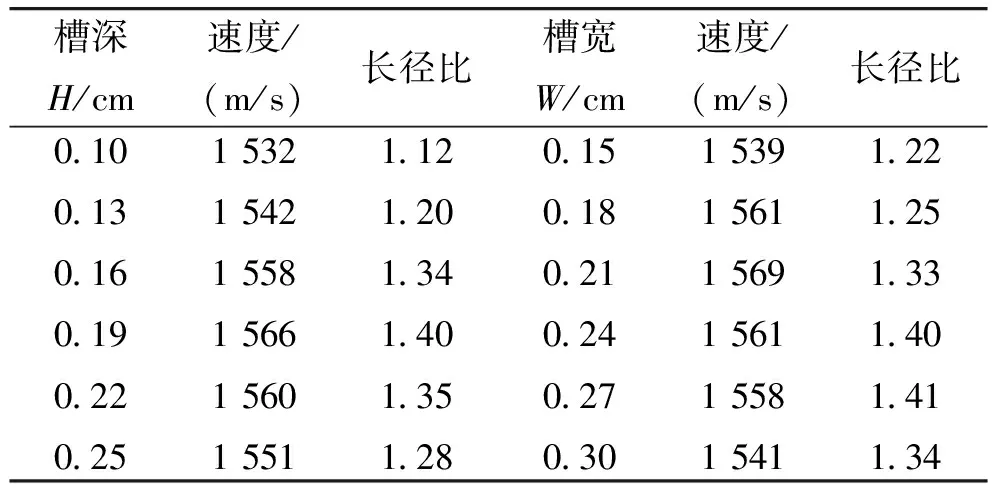
表5 不同槽深和槽宽的EFP速度及其长径比

表6 不同槽深的EFP形态
由计算结果可知,槽深由0.1 cm增加到0.25 cm,EFP的速度及长径比都呈先增大后减小的趋势。但槽深过大时,尾翼成形效果较差。当槽深为0.19 cm时,EFP速度及长径比都达到最大值,尾翼形态较好。
当槽长L=1.0 cm、槽深H=0.19 cm时,槽宽W依次取值为0.15 cm、0.18 cm、0.21 cm、0.24 cm、0.27 cm、0.3 cm进行计算,其结果见表5。不同槽宽的EFP形态见表7,EFP速度及长径比随槽宽的变化曲线如图3所示。

图2 EFP速度及长径比随槽深的变化曲线

表7 不同槽宽的EFP形态
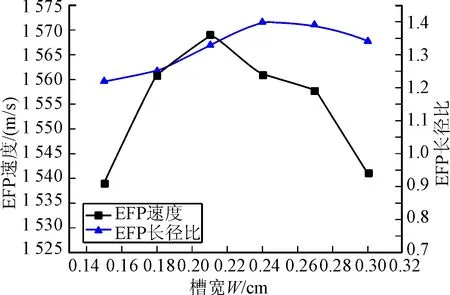
图3 EFP速度及长径比随槽宽的变化曲线
由模拟结果可知,槽宽由0.15 cm增加到0.30 cm,EFP的速度及长径比都呈现先增大后减小的趋势。当槽宽为0.24 cm时,EFP长径比达到最大值,虽其速度有所下降,但下降不明显,且其尾翼形态良好。
2.4 填充物材料对EFP形成尾翼的影响
当刻槽参数不变时,分析不同填充物材料对尾翼EFP的影响。当槽深为0.19 cm、宽为0.24 cm时,填充材料为铝合金、陶瓷、45钢,分别进行数值模拟。填充材料参数见表8,不同填充材料的EFP形态见表9,不同填充材料的EFP速度、长径比和尾翼厚度见表10。

表8 填充材料参数

表9 不同填充材料的EFP形态

表10 不同填充物材料的EFP速度和长径比
模拟结果表明,随着填充材料密度的增大,EFP速度及长径比都增大。尾翼厚度是影响弹丸飞行稳定性重要的因素[13],填充材料为45钢时,形成EFP尾翼厚度较大,尾翼成型效果较好。
3 总结
1)药型罩结构对形成尾翼型EFP影响明显,药型罩有刻槽且槽内有填充物时,EFP尾翼张的很开,形态较好。
2)槽宽W和槽深H对尾翼型EFP影响显著。当槽宽为0.048倍、槽深为0.038倍装药直径Dk时,形成的尾翼型EFP速度及长径比最大,尾翼形态较好。此结论只适用于中小口径聚能装药。
3)填充材料对尾翼型EFP也有影响,填充材料为45钢时,尾翼型EFP速度及长径比较大,尾翼成型效果较好。这对尾翼型EFP研究工作有一定的指导意义,数值模拟的结果还有待进行试验验证。
参考文献:
[1] 刘建青, 郭涛, 顾文彬, 等. 三点起爆形成尾翼EFP的数值模拟和实验研究 [J]. 爆炸与冲击, 2013, 33(1): 38-46.
[2] 陆鸣, 井志胜, 张端平, 等. 四点起爆形成带尾翼EFP的试验研究 [J]. 弹箭与制导学报, 2009, 29(1): 128-129.
[3] 于川, 董庆东, 孙承纬, 等. 带尾翼翻转型爆炸成形弹丸试验研究 [J]. 爆炸与冲击, 2003, 23(6): 561-564.
[4] BOUET T H, TARAYRE P, GUILLON J P. Study of a multi-point ignition EFP [C]∥National Defence Research Establishment. 15th International Symposium on Ballistics. Israel: [s. n. ]. 1995: 159-166.
[5] 林加剑, 沈兆武, 任辉启, 等. 贴隔板法形成尾翼型EFP的试验研究及数值模拟 [J]. 火炸药学报, 2009, 32(1): 74-78.
[6] 赵慧英, 沈兆武, 李成兵, 等. 带尾翼爆炸成型弹丸的新技术 [J]. 含能材料, 2006, 14(2): 102-104.
[7] WEIMANN K. Flight stability of EFP with star shaped tail [C]∥National Defence Research Establishment. 14th International Symposium on Ballistics. Queber: [s. n. ]. 1993: 755-763.
[8] 唐平江, 顾文彬, 罗智伟. 变壁厚壳体对形成带尾翼EFP的影响 [J]. 四川兵工学报, 2009, 30(1): 34-36.
[9] 门建兵, 蒋建伟, 万丽珍. 带尾翼EFP形成的三维数值模拟研究 [J]. 北京理工大学学报, 2002, 22(2): 166-168.
[10] 李裕春, 时党勇, 赵远. LS-DYNA基础理论与工程实践 [M]. 北京: 中国水利水电出版社, 2008: 264-282.
[11] 张先锋, 陈惠武, 赵有守. EFP冲击引爆带壳炸药数值模拟研究 [J]. 弹道学报, 2006, 18(1): 90-92.
[12] 张钧, 陈智刚, 李小军, 等. 变壁厚球缺罩杆式射流的形成与侵彻性能研究 [J]. 爆破器材, 2016, 45(1): 39-42.
[13] MALEJKO G, KUHNLE W G. Aerodynamic predictions for explosively formed penetrators with thick fins using an inviscid cfd code [C]∥AIAA. 32nd Aerospace Sciences Meeting & Exhibit. [S.l.:s.n.], 1994: 1-8.
