“长方体和正方体的认识”教学设计与评析
2017-05-02许月良旷海彬
文︳许月良旷海彬
“长方体和正方体的认识”教学设计与评析
文︳许月良旷海彬
由长沙市教育局主办,长沙教育学院和长沙市特级教师工作研究专业委员会、望城区教育局承办的长沙市小学名优教师“志愿支教、送教到县”活动在望城区长郡月亮岛学校举行。长沙市小学数学骨干教师、长沙市丁丽小学数学名师工作室成员旷海彬老师执教了“长方体和正方体的认识”,为参与活动的数学教师送上了一份精美的大餐,受到了现场听众的一致好评。旷老师的课堂教学至少有以下四个鲜明的特点。
一、教与学的目标明确
旷老师设计的教学目标非常明确。一是通过观察、猜想、操作、想象、推理等数学活动,学生自主探索长方体关于面、棱、顶点的特征,在教师的引导下,理解长方体长、宽、高的含义。二是立足想象,小组通过操作,自主探索、发现长方体顶点、棱、面之间的关系。三是在自主探索长方体和正方体特征的过程中,培养学生的空间想象力。每一个目标都注重学生的认识规律和特点,为圆满完成教学任务奠定了基础。
二、教与学的方法协调
旷老师的课堂设置了“激活经验,导入新课”“引导观察,了解特征”“合作学习,深入探究”“内化反思,拓展应用”等环节,通过师生互动、生生互动,充分发挥了师生的双主体作用,教师真正成为了学生学习的引导者和合作者,学生在合作探究的过程中享受了获取知识和方法的愉悦感。
三、教与学的兴趣浓厚
数学新课程理念告诉我们,数学教学活动必须建立在学生的认知发展水平和已有的经验基础之上。旷老师在教学中,让学习小组自主操作,尝试搭长方体,通过讨论交流、汇报学习成果,探讨能不能搭成长方体的原因,充分体现了数形结合的思想、分类思想和转化思想。课堂上,旷老师向学生提供了充分从事数学活动的机会,并深入到小组,帮助他们在探索和合作交流的过程中真正地理解并掌握了基本的数学知识和技能、数学思想和方法,获得了较为广泛的数学活动经验。
四、教与学的情感融洽
旷老师在教学过程中,始终采用赏识教育引领学生积极思维,关注学生的学习状态。如,当学生由具体实物抽象出面的特征时,给予恰到好处的鼓励和表扬;当个别学生表达出现障碍时,进行适当点拨,最后获得理想答案。在教的过程中,旷老师注重以问题为中心,以讨论阐释为主要方式,以思维为主线开展教学。整堂课学生积极参与,主动展示自己的思维成果,掌声和笑声不时地在教室里响起。学生真正成为了学习的主人,在享受学习的过程中,获得了运用知识的愉快感和成就感。
诚然,课堂教学和电影一样,是一门遗憾的艺术,永远没有尽善尽美。如果旷老师在课堂教学中提问时能更加关注全体学生,生生互动时能更加深入到学习小组指导,就更加完美了。让我们用毕生的精力去追求和构建富有生命活力的数学课堂,引领学生不断从狭隘走向广阔。
“长方体和正方体的认识”教学设计
师生在回顾对长方体与正方体的印象后,进入新课环节。
一、引导观察,了解特征
1.理清面
师:刚才我们说长方体有6个面,能不能给其他同学演示下,你是怎么数的?(引导有序数出来,并说清楚上、下、左、右、前、后)(板书:6个面)
2.认识棱、顶点
学生观察长方体与正方体后,找出它们都有12条棱、8个顶点。引导学生从无序到有序地数棱与顶点。
二、合作学习,深入探究
1.从棱开始,设计方案。
师:这里有3种不同长度的小棒,分别是16厘米、12厘米、9厘米。按照不同的数量搭配出16根,放进4个不同的袋子。请大家独立思考,下面的4个袋子,你认为哪些袋子里的小棒一定能够搭成长方体,哪些一定不能?
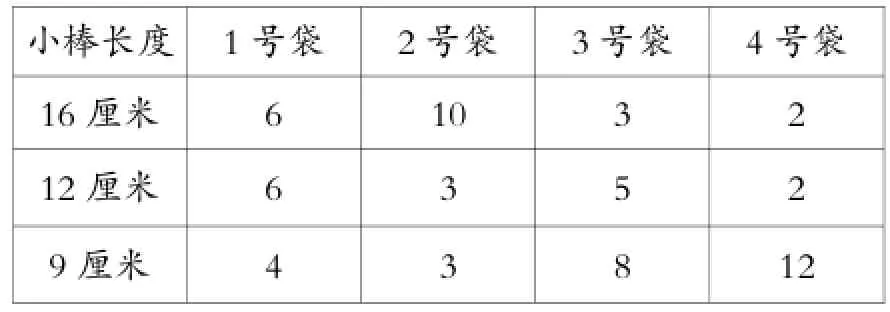
小棒长度1号袋2号袋3号袋4号袋16厘米6 10 3 2 12厘米63 5 2 9厘米4 3 8 12
学生思辨。
师总结:看来不仅要考虑小棒的数量,还要考虑它们的摆放位置。是不是那些真的都搭不成呢?有时候光在脑子里想不一定能弄清楚,我们一起试着搭一搭。
学生随机选择其中一个学具袋,合作搭长方体。
2.小组合作,动手操作。
活动要求:
(1)选出恰当数量的小棒。
(2)小组内先讨论不同长度的小棒应该放在长方体的什么位置,再合作搭建。
(3)完成后,思考:其他袋子里的小棒可不可以搭成?为什么?
学生自主操作,尝试搭长方体。
3.汇报交流。
(1)反馈方案1,弄清棱的位置。
邀请选择1号袋的学生代表上台展示。
师:你们是怎么选择小棒的?
生:16厘米的4根,12厘米的4根,9厘米的4根。
师:16厘米的6根,12厘米的6根,合起来不也正好是12根吗?为什么不选呢?
生:每种长度的小棒各要有4根。
师:那也就是把12根小棒分成了3组,对吗?(板书:分成3组,每组4根)这相等长度的4根,都放哪里了?(和学生一起找每组4根小棒的位置,总结出相对的棱长度相等)
师:再看看这相等的4条棱,它们还是互相平行的。(板书:平行)
(2)反馈方案2,巩固棱的特征。
师:2号袋子的小棒能不能搭成长方体?(不能)为什么?
师小结:看来要搭成长方体,不光只看有没有12条棱,还要注意这12条棱是否可以分成3组,每组都是4根。
(3)认识长、宽、高。
师:如果我们将这个长方体画在黑板上(课件出示图1),你看到了几个面?还有3个面哪去了?数一数这个图上有几条棱?还有3条棱去哪了?
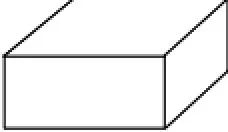
图1
学生通过想象,指出被遮挡的3条棱(课件辅助显示图2)。
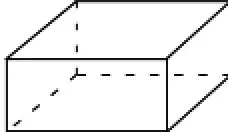
图2
师:请仔细看看这个画在平面上的长方体,它的上面和下面、左面和右面都是什么图形?为什么明明是长方形,却画成了平行四边形?(制造平面图形与实物图形的认知冲突,说明是透视的原因)
师:仔细看这个立体图,闭上眼睛想一想,再在脑海里回想一下这个长方体的样子,能想象出这个长方体的样子吗?
师:假如把其中1条棱隐藏,还能想象出它原来的样子吗?再隐去2条呢?请同学们思考:只要保留几条就能想象出原来的样子?
按照学生的想法留下3条。然后质疑这样是否可行,课件演示同一顶点3条棱还原长方体,再带领学生认识长、宽、高。
师总结:这3条棱数学上分别叫做长方体的长、宽、高。一般情况下,底面较长的那条棱是长,较短的是宽,垂直的是高,你能指一指这个长方体的长、宽、高吗?(不同位置摆放长方体,学生指出长、宽、高)
(4)头脑中搭长方体,得出面的特征。
师:(课件出示只有长、宽、高3条棱的图)从这幅图中,你能否想象出这个长方体6个面的大小?下面6个面中,哪些是这个长方体的面?哪些不是?为什么?

师小结:长方体相对的面大小相等,利用这一发现,只需要根据相交于一个顶点上的3条棱(长、宽、高),就能想象出长方体每一个面的大小。
(5)反馈方案3、方案4,拓展长方体类型。
师:如果一个长方体上只有②、④这两种不同的面,这个长方体是怎样的?
学生想象,教师适时给出两个面搭建的样子,学生想到这就是3号袋小棒搭成的长方体。
师:(举着2号袋小组搭建的模型)知道他们挑选的是哪些小棒吗?这个长方体与用1号袋搭的长方体相比,有什么特别之处吗?
生:1号袋搭出的长方体6个面都是长方形,3号袋搭出的长方体有两个面是正方形。
师:那这两个长方体之间有什么联系?(课件演示将棱长16厘米缩短为9厘米)现在还能选择上面图形中的两种,搭成4个大小相等的长方形,2个面是正方形的长方体吗?“确定了长、宽、高就确定了长方体”与“确定了2个相邻的面也就确定了长方体”,这两者之间有什么联系?有没有4个面是正方形,另外2个面是长方形的长方体呢?
生:没有可能。(结合特殊的长方体演示)
师:如果有4个面是正方形,那剩下的2个面也变成了正方形。有没有搭成6个面都是正方形的?
学生出示4号袋搭出的正方体,教师带领学生边想边看。
师:正方体6个面都是正方形,12条棱长度都相等。3号袋搭出的长方体与4号袋搭出的正方体之间有什么联系?(根据学生反馈,课件演示将棱长12厘米缩短为9厘米)
师总结:我们通过改变棱的长度就把长方体变成了特殊的长方体,最后又变成正方体。
三、内化反思,拓展应用
师:本节课学习后你有什么收获?闭上眼睛努力回想。(用卡纸遮住板书)现在请睁开眼睛,能将这个表填完整吗?
生说一个,教师揭开一个。
师:老师在很多长方体和正方体物体中,选择了一个物体并画出它的3条棱,请你想象并估计,这会是什么物体?
(1)出示只有长、宽、高(21厘米、15厘米、1厘米)3条棱的图。(实物:数学书)
(2)出示只有长、宽、高(21厘米、15厘米、0.01厘米)3条棱的图。(实物:数学书的一页纸)
师:纸虽然很薄,但也是长方体。当长方体中的高继续变小,小到什么时候,这个长方体就变成了长方形呢?
生:高为0。
师:是啊!长方形和长方体就在棱的变化中实现了完美变身。今天我们认识的长方体和正方体还只是立体图形世界中很少的一部分,立体图形世界还有许多知识等着我们去探索、去发现。
(作者单位:长沙市中小学教师发展中心长沙市雨花区天华寄宿制学校)
