思维在操作中得到放飞
——由一道思考题引发的思考
2017-05-02李蓉
文︳李蓉
思维在操作中得到放飞
——由一道思考题引发的思考
文︳李蓉
在人教版数学教材五年级上册多边形面积单元中,有一道特别有趣的思考题。如下:
(1)右图是用手工纸剪的一棵小树,它的面积是多少?(单位:cm)
(2)用一张长45cm、宽21cm的手工纸,能剪几棵这样的小树?

一、题目的背景
新课程在空间与图形板块安排了丰富的教学内容,而“位置”“图形的拼组”“观察物体”“图形与变换”这些内容都是新增的,学生学习时存在一定的困难。此题涉及图形拼组的知识,为了加深对图形的理解,学生需要在课堂上动一动手。尤其是解决第二问,如果采用画草图、剪小树等直观手段,学生可以打开思路,得到多样的算法。
二、题目的分析
此题综合性非常强,第一问是考查学生灵活运用基本图形面积计算公式的能力,第二问则是考查学生能否将面积计算的知识运用于生活实际,这是本题的难点。很多学生会用大图形面积除以小图形面积的思维定势来解决,而答案不是这样的。要很好地解决第二问,就必须提供充足的操作材料和时间,让学生通过动手操作开阔思路,活跃思维,使思考更深刻。
三、题目的解决
第一问的解答并不难,就是计算要细心,因为图形中的信息非常多,学生容易漏看或错看(如将长方形的长看成9厘米),还要熟记基本图形的面积计算公式。教师可以让学生说说这棵小树是由哪些基本图形组成的。学生通过观察知道此图由一个三角形、两个梯形和一个长方形组成。由于学过组合图形的面积计算,学生的方法可以有多种。
第二问的解答,不要急于给学生操作材料和答案,而是要让学生先独立尝试。上课时,果然不出我所料,有学生很快就计算完了。

图1
方法1:45×21÷48.6≈19(棵)。
课件出示图1,老师问学生:都同意吗?学生表示都同意。老师质疑,指出树干左右两边空白的部分还能再剪小树吗?学生有的说不能,零零碎碎不能再用;有的建议拼起来再剪;有的则反驳不能拼起来再剪。
这时,有很多学生指出方法1有问题,除了小树的面积,旁边的空白部分因为被剪成了零零碎碎的,不能再剪成小树了。老师肯定了学生的想法,提出小树是不规则的图形,不能简单地用大长方形面积除以小树的面积,并提问:“那应该怎么去想呢?”
学生想到先算一棵小树所占的长方形的面积,再除。
方法2:小树的高有3+3+3+6=15(厘米),宽有4+4=8(厘米),45×21÷(15×8)≈7(棵)。
师:这个结果大家都同意吗?
通过刚才的分析,学生们对这个结果还是不敢肯定。有学生提出,如果有一棵这样实际大小的小树让他在纸上摆一摆就好了。学生由于之前练习过的内容都是规则图形,且适合大图形面积除以小图形面积得到结果。而此题采用常规思路不合适。这时如果用实际大小的长方形纸和小树摆一摆,学生能更直观地认识大图形与小树之间的关系。于是,我趁热打铁,让学生们拿出信封里的若干棵小树和手工纸(如题所述的大小),2人一组,一人摆,一人贴,再列出算式,看一张手工纸能剪多少棵小树。
一段时间后,我收集好学生的作品,让他们到讲台上逐一汇报。
学生汇报小树竖着摆(如图2所示),得到算式:45÷8=5(棵)……5(厘米)。
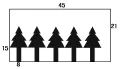
图2
学生质疑:上面部分和右边部分都不能剪了,很浪费。认为要把小树横着摆(如图3所示)。得到算式:手工纸的长可以排45÷15=3(棵),手工纸的宽可以排21÷8=2(棵)……5(厘米),一共能剪3×2=6(棵)。
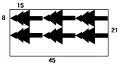
图3
讲到这里,学生已经基本明白不能简单地用手工纸的面积除以小树的面积,而是要考虑实际的排列,认为方法1和方法2不对。这时有学生质疑:如果对小树进行交叉颠倒摆放,是否会剪得多些呢?
学生动手尝试交叉颠倒摆放,发现手工纸的宽可以排1棵,长可以排8棵,用去4×8+4× 2=40(厘米),剩下45-40=5(厘米),再剪一棵树要8厘米,就不够了(如图4所示)。

图4
有学生在图3基础上得到图5这样的排法,因为宽还多5厘米,可以在中间插入2棵,所以一共可以剪:3×2+2=8(棵)。
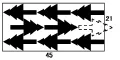
图5
还有学生按图6这样排,发现最多可以排9棵。两棵树交叉放,高是15+6=21(厘米),宽排出2棵;长方形的长排出45÷8=5(棵)……5(厘米),共9棵。

图6
孩子们的智慧是无穷的,只要教师适时挖掘,就会有令人惊异的效果。这时,老师问:通过刚才的拼摆,怎样剪才能剪出更多的小树呢?学生思考,师生一起小结:合理安排空间,交叉剪。
孩子们受到启发,有个学生回家思考后,竟摆出了10棵(如图7所示)。

图7
其实,仔细阅读题中的问题“能剪出几棵这样的小树?”我们发现这里问的是几棵并不是最多几棵。可见此问题是开放的,体现解决问题策略的多样化。对此,老师针对不同学生可以有不同的要求,5棵、6棵、8棵、9棵、10棵都是应该获得支持的答案。而对于“45×21÷ 48.6≈19(棵)”和“45×21÷(15×8)≈7(棵)”的方法则需要引导、纠正,因为这是对剪拼图形片面的认识。尽管是思考题,5棵、6棵还是应作为全体学生的基本要求。至于交叉摆放节省空间,这在生活中有广泛的应用,应该让学生通过具体操作进行体验。所以,引导学生思考了,懂得了如何巧妙利用空间的基本原理,可以为以后的几何学习奠定良好的基础。
(作者单位:长沙市芙蓉区东郡小学)
