频域两尺度簇发振荡结构及其动力学机制
2017-05-02夏付兵韩修静毕勤胜
夏付兵,韩修静,瞿 汭,毕勤胜
(江苏大学 土木工程与力学学院,江苏 镇江 212013)
频域两尺度簇发振荡结构及其动力学机制
夏付兵,韩修静,瞿 汭,毕勤胜
(江苏大学 土木工程与力学学院,江苏 镇江 212013)
以非自治杜芬-范德波尔振子为例,探讨了当外激励频率与系统固有频率之间存在量级差异,也即存在频域不同尺度时的快慢耦合效应。通过固定低频激励项,分析了快子系统的稳定性和分岔行为,得到了对应的两参数分岔集。将分岔集划分为5个区域,并分析了与各区域相关的簇发振荡模式。揭示了对称式折/折和对称式亚临界Hopf/亚临界Hopf等点-点式簇发的行为,以及对称式亚临界Hopf/极限环折和对称式延迟超临界Hopf /延迟超临界Hopf等点-圈式簇发的行为。研究结果表明:快子系统的多解和多分岔共存是诱发各种对称式簇发振荡模式的重要原因。
两时间尺度;点-点式簇发;点-圈式簇发;分岔机理
0 引言
多时间尺度问题在物理、化学、生物以及工程技术等领域普遍存在[1-4]。大阻尼条件下的范德波尔振子是典型的两时间尺度非线性系统,由快子系统和慢子系统耦合而成,含有“快”、“慢”两种不同的时间尺度,而著名的范德波尔型“张弛振动”正是快、慢子系统之间相互作用的产物。这种类似的快慢耦合现象存在很多领域内。例如,在化学反应中,当各反应物的反应速率存在着明显的量级上的差异时,整个反应过程会呈现出快慢耦合的振荡模式[5];而当各反应物的浓度存在着量级上的差异时,往往也会导致类似的振荡模式[6]。特别地,在生物神经系统中,神经元的簇放电活动表现为重复放电态与静息态的交替出现,这是一个典型的多时间尺度非线性现象[7]。
长期以来,如何分析不同时间尺度之间的相互作用,进而揭示不同时间尺度的耦合振动现象的本质,一直是学者们关注的重要问题。直到文献[8]提出快慢分析法,该问题才有了较为圆满的解答。快慢分析法为多时间尺度耦合效应的定性解释提供了重要的理论框架,其基本思想是将多时间尺度系统进行“解剖”,即先确认多时间尺度系统的快、慢子系统;然后将快、慢子系统分开讨论;进而用分岔理论揭示系统在具有大振幅特征的激发态和具有小振幅特征的沉寂态之间相互转迁的动力学机制。文献[9]将快慢分析法应用于簇发的分类,以此拓展了系统在激发态和沉寂态之间转迁的各种可能的诱发机制。基于文献[8]的快慢分析法和文献[9]的簇发分类,国内外学者采用试验、理论/数值分析或将试验与理论/数值分析相结合的方法[10-12],对各种快慢耦合系统进行了深入研究。
然而到目前为止,大部分的研究工作主要针对自治系统。对于非自治系统而言,其快慢耦合的分岔机制较为复杂,需进一步探讨。基于此,本文以一类含有低频外激励项的非自治系统[13]为例,探讨由于低频外激励的存在而诱发的频域两尺度耦合效应,揭示复杂动力学行为及其产生机制,尤其是各种可能的频域两尺度簇发振荡模式及其产生机制,并对各种簇发振荡模式进行分类。
1 分岔分析
考虑杜芬-范德波尔系统,其动力学演化方程[13]为:
(1)
其中:p,α,β=O(1)为实参数;γcos(ωt)为低频激励项。由于激励项的频率远小于系统的固有频率,系统(1)包含了高、低两频域尺度,分别对应系统的快子系统和慢子系统。通过固定低频激励项,可得到如下快子系统:
(2)
其中:d为控制参数,d=γcos(ωt)。慢子系统(慢变量)由低频外激励γcos(ωt)决定。
根据快慢分析法,快子系统(2)的动力学行为对快慢耦合振动行为具有重要的影响。因此,本部分探讨快子系统(2)关于控制参数d的稳定性和分岔行为。
显然,快子系统的平衡点可以表示为(x0,0),其中,x0由方程
(3)
的实根决定。方程(3)的根判别式为Δ=d2/4β2+α3/27β3。

27βd2+4α3=0
(4)
时,方程(3)有2个不等的实根。此时,快子系统发生了折分岔。

图1 快子系统(2)在(d,α)参数平面上的分岔集, 取实参数p=-1.0, β=1.0
图1为快子系统(2)在(d,α)参数平面上的分岔集,取实参数p=-1.0,β=1.0。如图1所示,LP1和LP2是由式(4)决定的两条折分岔曲线,他们相切于余维2cusp点,CP=(0,0)。这两条折分岔曲线和直线α=-4.0围成了一个含有平衡点E0和E±的“三角形”区域。当参数从该区域内穿越LP1(LP2)时,平衡点E0和E+(E-)碰撞消失。因此,LP1的左侧区域只有一个平衡点E-,而LP2的右侧区域只有一个平衡点E+。
当判别式Δ>0,即当27d2+4α3/β>0时,系统仅有一个平衡点E0。特别地,当α,β同号时,判别式Δ>0恒成立。图1中的β=1.0,因此,在图1中α>0区域内,快子系统只含有一个平衡点E0。

d=±(α+β), α>0
(5)
时,与E0相对应的特征方程具有一对纯虚特征根。因此,此时平衡点E0可能会发生Hopf分岔。采用类似的分析方法,可得平衡点E±的Hopf分岔条件:
d=±(α+β), -3<α<0。
(6)
为了进一步揭示快子系统的分岔行为,图1给出了p=-1.0,β=1.0时的快子系统在(d,α)参数平面上的分岔集。图1中:BT1、BT2是余维2Bogdanov-Takens分岔,其坐标是(dBT1,αBT1)=(-2.0,-3.0),(dBT2,αBT2)=(2.0,-3.0);GH1、GH2是余维2广义Hopf分岔点,其坐标是(dGH1,αGH1)=(-4.0,3.0),(dGH2,αGH2)=(4.0,3.0);supH1、supH2是平衡点E0的超临界Hopf分岔曲线。α=0上的A、B、C、D这4个点将亚临界Hopf分岔曲线及LPC曲线分为上下两部分:曲线上半部分中subH11和subH21是平衡点E0的亚临界Hopf分岔曲线,LPC11(LPC21)是由subH11(subH21)所产生的不稳定极限环的鞍结分岔;曲线下半部分中subH12和subH22分别是平衡点E-和E+的亚临界Hopf分岔曲线,LPC12(LPC22)表示由subH12 (subH22)所产生的不稳定极限环的鞍结分岔;E=(0,-1.3)是LPC曲线下端的最低点。
基于基本的分岔理论,同时考虑到图1所示的快子系统的分岔特性,可将参数平面(d,α)划分为5个不同的参数区域(见图1中I~V)。由于这5个区域对应着快子系统不同的动力学行为,因此,当α属于不同的参数区域时,系统(1)可能会产生不同的簇发振荡模式。
2 点-点式簇发
通常情况下,簇发因系统在不同的吸引子之间相互转迁而形成,故根据吸引子的类型可将簇发分为点-点式、点-圈式和圈-圈式等几大类。本节探讨点-点式簇发振荡模式,这类簇发由轨线在不同的平衡点吸引子之间相互转迁而形成。为了便于分析,从本节开始,固定参数p=-1.0,β=1.0。
2.1 对称式“折/折”簇发
当α=-3.2,γcos(ωt)=2.3cos(0.01t)时,图2a给出了α属于区域Ⅰ时系统(1)的典型簇发振荡模式。根据快慢分析法,图2b给出了此时快子系统关于慢变量d的稳定性和分岔行为。图2b中,粗实线和虚线分别表示稳定和不稳定的平衡点,构成了一条具有两个折分岔点的S形平衡点曲线。为了进一步分析簇发的动力学机制,将分岔图与簇发的转换相图[15]进行叠加,如图2b所示。
由于折分岔值dLP2=2.2,因此当振幅γ>2.2时(例如取γ=2.3),慢变量γcos(ωt)能够穿越折分岔点。随后,折分岔引起系统的轨线在上、下稳定支之间来回跳跃(见图2b中细实线),由此形成了点-点式簇发(见图2a)。考虑到轨线的“跳跃”由两个折分岔加以调控及其对称性,因此,这种簇发可以命名为对称式“折/折”簇发。且当α=-3.2时,参数α属于区域Ⅰ,而区域Ⅰ中只有两条折分岔曲线。因此,图2b给出的是区域Ⅰ中典型的稳定性和分岔行为。故而,基于此所得的簇发行为(见图2a)是区域Ⅰ内簇发振荡模式的典型代表。

图2α属于区域Ⅰ时系统(1)的簇发振荡模式
2.2 对称式“亚临界Hopf/亚临界Hopf”簇发
当α=-1.5,γcos (ωt)=0.7cos (0.01t)时,参数α属于区域Ⅱ。图3a给出了区域Ⅱ内典型的分岔图,其中粗实线和虚线的含义同图2b。如图3a所示,S形平衡点曲线被两个折分岔点分为上、中、下3支,其中上、下稳定支因亚临界Hopf分岔而失稳,分岔值分别为dsubH12=-0.5和dsubH22=0.5。因此,当振幅γ>0.5(例如γ=0.7)时,慢变量可穿越亚临界Hopf分岔点,而这会进一步引起系统在上、下平衡点稳定支之间的来回转迁(见图3a中细实线)。于是,一种不同于图2a的簇发振荡模式产生,考虑到轨线的转迁由亚临界Hopf分岔(而不是折分岔)加以调控,因此,这种簇发可以命名为对称式“亚临界Hopf/亚临界Hopf”簇发,图3b所得到的簇发行为是区域Ⅱ内典型的簇发振荡模式。
点-点式簇发是一大类较为简单的簇发振荡模式。类似的簇发现象在文献[16-18]中均有报道。这类簇发有一个共性,即簇发所呈现出的连续尖峰振荡与轨线向平衡点吸引子收敛的速率有关,而与稳定的极限环无关(事实上,多数情况下快子系统并不存在极限环吸引子,例如图2b和图3a)。

图3α属于区域Ⅱ时的簇发振荡模式
3 点-圈式簇发
本节探讨轨线在平衡点和极限环之间相互转迁而诱发的簇发振荡模式,即点-圈式簇发。这类簇发振荡模式中的参数α与区域Ⅲ~Ⅴ有关。
3.1 对称式“亚临界Hopf/极限环折”簇发
探讨参数α属于区域Ⅲ时的簇发振荡模式如图4所示。该区域分岔图与簇发的转换相图的叠加见图4a。在图4a中,当d=∓0.5时,S形平衡点曲线的上、下稳定支因亚临界Hopf分岔而失稳,同时生成了一个不稳定的极限环。当d=∓0.5时,该不稳定的极限环与稳定的极限环在图4a分岔点LPC12、LPC22(对应图1中标注,下同)处碰撞、消失,即发生了极限环的折分岔。图4b给出了区域Ⅲ内典型的簇发振荡模式。
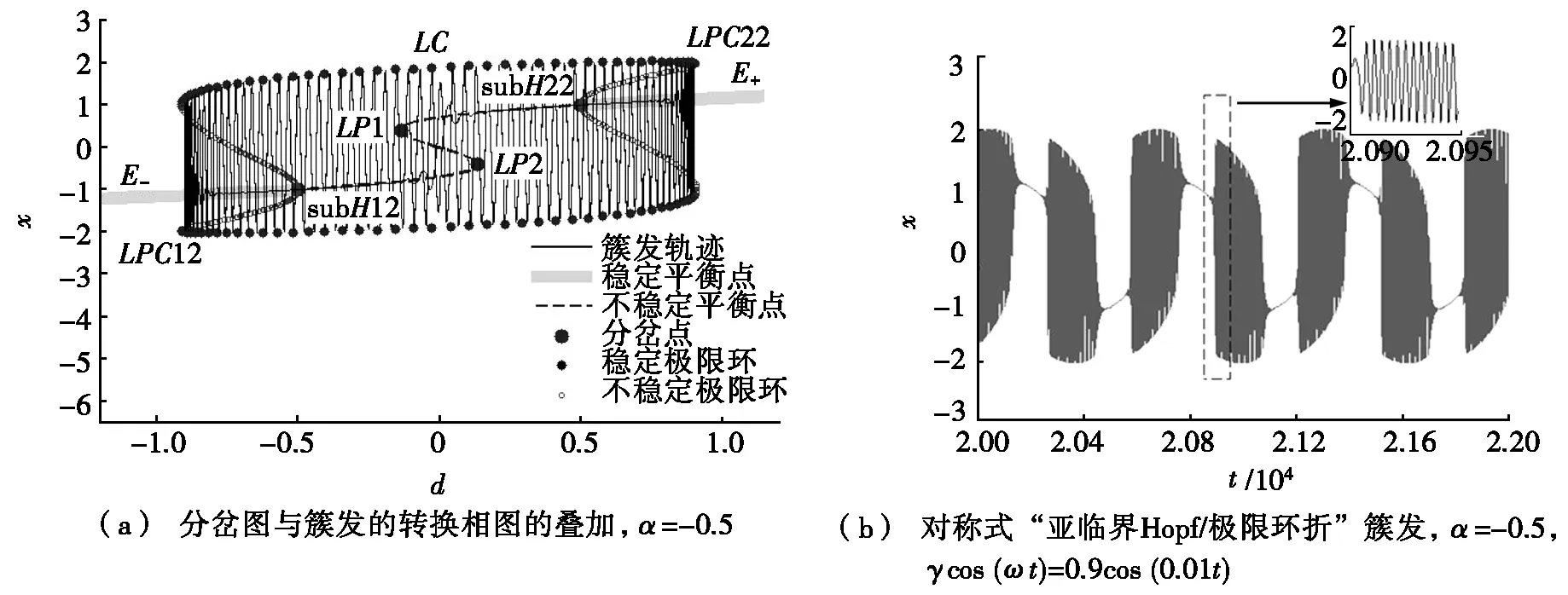
图4 α属于区域Ⅲ时的簇发振荡模式
在图4a中LPC12分岔的左侧,E-是系统唯一的吸引子,因此当慢变量递减地穿越LPC12时,系统的轨线向E-转迁。当慢变量穿越subH12时,E-失稳。于是,轨线离开E-,向激发态LC转迁。随后,在时间序列中可以观测到与LC相关的连续的尖峰。当慢变量穿越LPC22时,LC消失,连续的尖峰因此而终止。于是,轨线又向E+转迁,并由此开始了簇发的下一个演化过程。
考虑到系统因亚临界Hopf分岔从沉寂态转迁到激发态,随后又因极限环的折分岔返回沉寂态,同时注意到簇发的对称性,因此区域Ⅲ中的簇发振荡模式可以命名为对称式“亚临界Hopf/极限环折”簇发。
α属于区域Ⅳ时的簇发振荡模式,如图5所示。图5a给出了区域Ⅳ中典型的单参数分岔图。与区域Ⅲ相比,区域Ⅳ缺少了两条折分岔曲线。因此,当参数α从区域Ⅲ进入区域Ⅳ时,原先的具有两个折分岔点的S形平衡点曲线会被慢慢“拉直”,演变为图5a所示的较为平滑的平衡点曲线。

图5 α属于区域Ⅳ时的簇发振荡模式
然而,区域Ⅳ中平衡点曲线的这些变化并不会引起簇发行为的定性变化。其原因为:平衡点的折分岔在对称式“亚临界Hopf/折极限环”簇发的产生过程中没有起到任何作用;区域Ⅳ中的沉寂态、激发态以及连接它们的分岔模式均没有改变。因此,当α属于区域Ⅳ时,系统只能产生与区域Ⅲ动力学机理相同的簇发振荡模式,即对称式“亚临界Hopf/极限环折”簇发,见图5b。
3.2 对称式“延迟超临界Hopf /延迟超临界Hopf”簇发
参数α属于区域Ⅴ时的簇发振荡模式如图6所示。当α=3.5时,α属于区域Ⅴ,图6a给出了此时的簇发振荡模式。为了揭示簇发的动力学机制,图6b进一步给出了α=3.5时快子系统关于慢变量d的单参数分岔图,其中,LC是因超临界Hopf分岔(分岔值是dsupH1,2=∓4.5)而产生的稳定的极限环。显然,图6b给出的是区域Ⅴ中典型的稳定性和分岔行为,故基于此所得到的簇发行为(见图6a)是区域Ⅴ内的簇发振荡模式的典型代表。
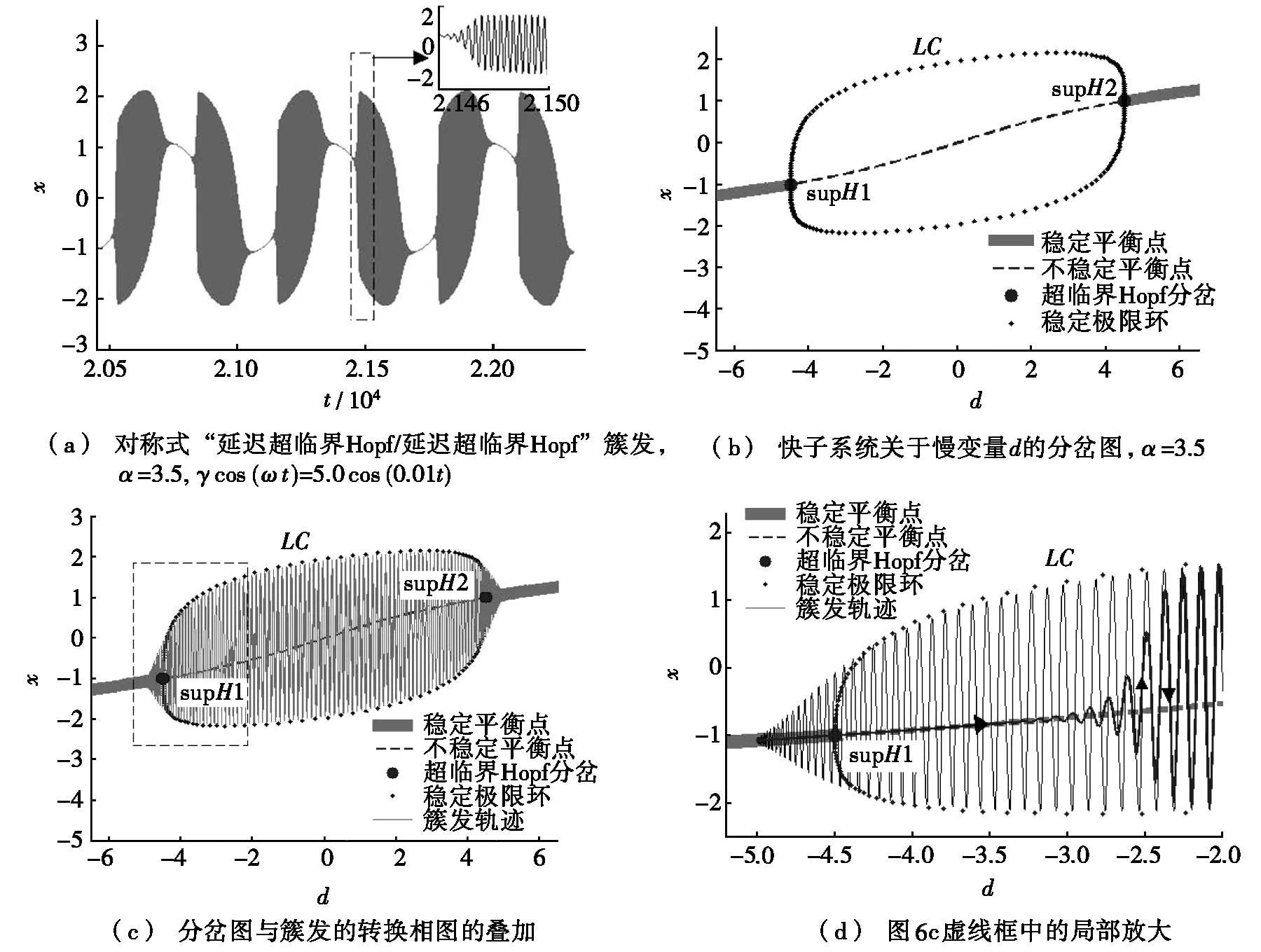
图6 α属于区域Ⅴ时的簇发振荡模式
如图6b所示,supH1和supH2将参数d分为3个区域,即位于supH1和supH2之间的激发态区域以及在其左右两侧的沉寂态区域。显然,这3个区域均仅含一个吸引子,因此系统不存在滞后现象。这与区域Ⅰ~区域Ⅳ的情形不同。
大量的数值模拟表明:当慢变量穿越Hopf分岔点supH1和supH2进入激发态区域时,轨线会在不稳定的E0上逗留一段时间,由此形成了平衡点E0与极限环吸引子LC之间的滞后。随后,轨线离开E0,向激发态LC转迁(见图6d)。这种现象即所谓的延迟Hopf分岔现象[19],与慢变量穿越分岔点有关,可根据非标准分析[20]和WKB法[21]等理论加以理解。考虑到对称性,同时注意到轨线因延迟Hopf分岔进入和退出激发态,因此,图6c所示的簇发振荡模式可以命名为对称式“延迟超临界Hopf /延迟超临界Hopf”簇发。
4 结论
(1)与通常频域尺度下的杜芬-范德波尔系统相比,频域两尺度下的杜芬-范德波尔系统可以产生更加复杂的动力学行为,例如多种点-点式和点-圈式簇发振荡模式。
(2)快子系统呈现出较为丰富的稳定性和分岔行为,由此导致沉寂态、激发态以及连接他们的分岔模式的多样性,而这是对称式“折/折”型、对称式“亚临界Hopf/亚临界Hopf”型、对称式“亚临界Hopf/极限环折”型以及对称式“延迟超临界Hopf /延迟超临界Hopf”型等多种簇发振荡模式产生的重要原因。
[1] 陈章耀,王亚茗.切换断路时间对非线性切换系统振荡特性的影响[J].河南科技大学学报(自然科学版),2016,37(5):87-90.
[2] BI Q S.The mechanism of bursting phenomena in Belousov-Zhabotinsky (BZ) chemical reaction with multiple time scales[J].Science China technological sciences,2010,53(3):748-760.
[3] COURBAGE M,MASLENNIKOV O V,NEKORKIN V I.Synchronization in time-discrete model of two electrically coupled spike-bursting neurons[J].Chaos,solitons and fractals,2012,45(5):645-659.
[4] CROUCH R,OSKAY C.Accelerated time integrator for multiple time scale homogenization[J].International journal for numerical methods in engineering,2015,101(13):1019-1042.
[5] RAKARIC Z,KOVACIC I.Mechanical manifestations of bursting oscillations in slowly rotating systems[J].Mechanical systems and signal processing,2016,81:35-42.
[6] LI X H,BI Q S.Bursting oscillations and the bifurcation mechanism in oxidation on platinum group metals[J].Acta physica sinica,2012,61(2):88-96.
[7] SHI X,SUN X J,LU Q S,et al.Cluster synchronization and rhythm dynamics in a complex neuronal network with chemical synapses[J].International journal of non-linear mechanics,2014,70:112-118.
[8] RINZEL J.Bursting oscillator in an excitable membrane model[M]//SLEEMAN B D,JARVIS R J.Ordinary and partial differential equations.Berlin:Springer,1985:304-316.
[9] IZHIKEVICH E M.Neural excitability,spiking and bursting[J].International journal of bifurcation and chaos,2000,10(6):1171-1266.
[10] GU H G,CHEN S G,LI Y Y.Complex transitions between spike,burst or chaos synchronization states in coupled neurons with coexisting bursting patterns[J].Chinese physics b,2015,24(5):281-292.
[11] 陆惠玲,李绍龙,张正娣.参数激励下分段线性两尺度系统的分岔[J].河南科技大学学报(自然科学版),2015,36(6):71-74.
[12] 古华光,朱洲,贾冰.一类新的混沌神经放电的动力学特征的实验和数学模型研究[J].物理学报,2011,60(10):74-85.
[13] UDWADIA F E.First integrals and solutions of Duffing-van der Pol type equations[J].Journal of applied mechanics,2014,81(3):100-120.
[14] 陆启韶,彭临平,杨卓琴.常微分方程与动力系统[M].北京:北京航空航天大学出版社,2010:62-64.
[15] 陈章耀,张晓芳,毕勤胜.周期激励下Hartley模型的簇发及分岔机制[J].力学学报,2010,42(4):765-773.
[16] HAN X J,BI Q S,ZHANG C,et al.Delayed bifurcations to repetitive spiking and classification of delay-induced bursting[J].International journal of bifurcation and chaos,2014,24(7):1450098.
[17] HAN X J,BI Q S.Bursting oscillations in Duffing’s equation with slowly changing external forcing[J].Communications in nonlinear science and numerical simulation,2011,16(10):4146-4152.
[18] DUAN L X,LU Q S,CHENG D Z.Bursting of Morris-Lecar neuronal model with current-feedback control[J].Science in China,2009,52(3):771-781.
[19] HAN X J,XIA F B,JI P,et al.Hopf-bifurcation-delay-induced bursting patterns in a modified circuit system[J].Communications in nonlinear science and numerical simulation,2016,36:517-527.
[20] BENOIT E,CALLOT J L,DIENER F,et al.Chasse au canard[J].Lecture notes in mathematics,1983,985:449-494.
[21] HOLMES M H.Introduction to perturbation methods[M].New York:Springer,1999:806-807.
国家自然科学基金项目(11632008,11572141,11502091,11472115,11402226)
夏付兵(1990-),男,安徽安庆人,硕士生;韩修静(1983-),男,江苏宿迁人,副教授,博士,硕士生导师,主要研究方向为非线性动力学.
2016-09-18
1672-6871(2017)04-0084-06
10.15926/j.cnki.issn1672-6871.2017.04.017
O322
A
