广义超立方体的广义连通度

张倩华，林上为

(山西大学 数学科学学院，山西 太原 030006)

广义超立方体的广义连通度

张倩华，林上为

(山西大学 数学科学学院，山西 太原 030006)

k元n方体是著名的超立方体网络的推广。针对k元n方体的广义3-连通度问题，证明了对任意的整数k≥3和n≥1，k元n方体中存在2n-1棵内部不交的连接任意3个顶点的树。

超立方体；连通度；可靠性；树；路

0 引言

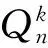
连通度是图论的核心内容之一，广义连通度作为连通度的一个推广，被广泛运用于互连网络中，可用来测量网络的可靠性。近年来，很多图的广义连通度已经得到研究[7-8]。然而，k元n方体的广义连通度研究较少。本文将在k≥3的条件下，确定k元n方体的广义3-连通度。

1 预备知识

V={x1x2…xn:xi∈{0,1,2,…,k-1},i=1,2,…,n}。

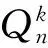
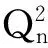
定义2[9]给定一个图G和G的顶点子集X，若G-X不连通或平凡，则称X为G的一个顶点割。G的连通度κ(G)是G中最小顶点割的顶点个数。

熟知连通度有如下的等价定义：

定义3[9]对V(G)的每个2元子集S={x,y}，用κ(S)表示G中内部不交的(x,y)-路的最大数目。图G的连通度κ(G)=min{κ(S):S是V(G)的一个2元子集}。

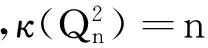
连通的无圈图称为树，路是特殊的树。

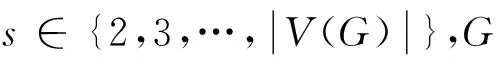
注意，κ2(G)=κ(G)，因此，广义连通度是连通度的一个推广。而κn(G)恰恰就是G中边不相交的生成树的最大数目。广义连通度不仅是一个自然的组合度量，而且它在实际应用中也可以激发人们的兴趣。近年来，图的广义连通度已经得到很多研究[9-10]。

定理2[10]n维超立方体Qn的广义3-连通度为n-1，即κ3(Qn)=n-1。

下面的两个引理将在主要结论的证明中用到。

引理1[9]给定图G和G中的一个顶点x。若κ(G)=k，则对G中任意k个顶点y1,y2,…,yk，G都含(x,y1)-路P1，(x,y2)-路P2，…，(x,yk)-路Pk，使得对所有的i≠j有V(Pi)∩V(Pj)={x}。

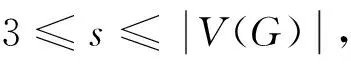
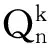
2 主要定理及其证明

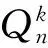
情形1 x,y,z∈V0。

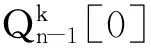
情形2 x,y∈V0,z∈Vp，其中p∈{1,2,…,k-1}。

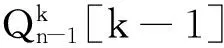
情形3x∈V0,y∈Vp,z∈Vq，其中p,q∈{1,2,…,k-1}且p≠q。

情形3.1k≥4。

情形3.2k=3。

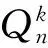
当n=2时，2n-1=3，3棵内部不交的S-树分别为：T1=(00,01,11,21,22),T2=(00,02,12,22)+(12,11),T3=(00,10,20,22)+(10,11)。

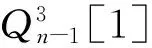
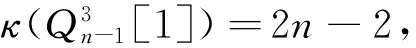
3 结束语

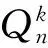
[1] 徐俊明.组合网络理论[M].北京:科学出版社,2007.

[2] 徐保根,张亚琼,汤友良.关于图的符号边控制数的一些结论[J].河南科技大学学报(自然科学版),2012,33(4):74-77.

[3] ESFAHANIAN A H.Generalized measures of falut tolerance with application ton-cube networks[J].IEEE transactions on computers,1989,38(11):1586-1591.

[4] WANG S Y,LI J,YANG Y X.Unchanging the diameter ofk-aryn-cube networks with faulty vertices[J].International journal of computer mathematics,2015,92(1):15-28.

[5] GU M M,HAO R X,LIU J B.On the extraconnectivity ofk-aryn-cube networks[J/OL].International journal of computer mathematics,2015.[2016-07-20].http://dx.doi.org/10.1080/00207160.2015.109107.

[6] WANG F,ZHANG H.Matchings extend to Hamiltonian cycles ink-aryn-cubes[J].Information sciences,2015,305:1-13.

[7]KOH K M,DONG F M,NG K L,et al.Graph theory:undergraduate mathematics[M].Singapore:World Scientific Publishing,2015.

[8] LI H Z,LI X L,SUN Y F.The generalized 3-connectivity of Cartesian product graphs[J].Discrete mathematics and theoretical computer science,2012,14:43-54.

[9] CHARTRAND G,OKAMOTO F,ZHANG P.Rainbow trees in graphs and generalized connectivity[J].Networks,2010,55:360-367.

[10] LI S S,LI X L,ZHOU W L.Sharp bounds for the generalized connectivityκ3(G)[J].Discrete mathematics,2010,310:2147-2163.

国家自然科学基金项目(61202017);中国博士后基金项目(2012M510579)

张倩华(1992- ),女，山西长治人，硕士生;林上为(1981-),男,浙江温州人,副教授,博士，硕士生导师,主要研究方向为图论及其应用.

2016-08-12

1672-6871(2017)04-0090-04

10.15926/j.cnki.issn1672-6871.2017.04.018

O157.5

A