模糊物元分析的电动汽车城市充电站规划
2017-05-02郑春燕
郑春燕,郭 栋,张 海,杨 坤,徐 艺
(山东理工大学 a.商学院;b.交通与车辆工程学院,山东 淄博 255049)
模糊物元分析的电动汽车城市充电站规划
郑春燕a,郭 栋b,张 海b,杨 坤b,徐 艺b
(山东理工大学 a.商学院;b.交通与车辆工程学院,山东 淄博 255049)
为了解决充电站选址决策的多准则、不相容问题,研究了一种基于模糊物元分析理论的多方案、多特征的电动汽车城市充电站选址决策方法,构建了充电站选址决策评价指标体系并确定了各指标的权重。通过建立多个充电站备选点的多维复合模糊物元矩阵,经关联变换将电动汽车充电站选址由不相容问题转化为相容问题,以实现对多个充电站备选点的优选。实例分析表明:针对4个备选点确定5个评价指标值,通过模糊物元分析得到备选点2的关联度最高,为8.625。
充电站;选址;模糊物元;电动汽车;规划
0 引言
目前,电动汽车产业还处于发展初期,配套充电设施的合理规划是保障电动汽车普及和应用的重要工作。充电站的选址布局,直接关系到投资方的利益和用户的充电便利性,对基础建设的投资、运行的可靠性和经济性,以及充电站的日供电质量和容量,有着举足轻重的作用[1]。如何实现电动汽车充电站选址优化布局,已成为城市规划及交通部门重点关注的问题。
针对电动汽车充电站选址规划,文献[2]预测了区域电动汽车的总量和分布情况,并依据交通流量守恒定理将动态的电动汽车数量转换为常数,用遗传算法将建立的年费用最小模型进行求解,确定充电站的容量和选址。文献[3]将博弈论用到充电站选址规划布局方案评价中,采用原对偶路径跟踪法求解建立的线性规划模型,为充电站选址方案提供了理论依据。文献[4]综合考虑土地等建设成本及人员工资等运行成本,以充电站初始建设成本和运行成本最低为目标,建立了电动汽车充电站选址定容新模型。
充电站选址决策需要考虑的因素众多,且各因素之间关系模糊,存在较大的不确定性,属于典型的不相容问题。依靠传统的人为主观判断完成充电站选址,或者借助一般的数学方法解决此不相容问题,均存在较大的局限性[5-7]。本文基于模糊物元分析理论[8-9],通过关联变换将充电站选址决策规划转化为相容问题,从而为充电站选址提供科学的指导。
1 充电站选址决策评价指标体系的确定
充电站选址决策评价指标体系的确定,应兼顾效益和安全[10-11]。参考加油站选址的原则,确立了5个指标。
(Ⅰ)建设成本。建设成本指投资建设充电站全部设施的基础设施成本、配电设施成本及土地费用等,还包括人员培训费等运营成本。
(Ⅱ)设计规模。设计规模按照充电站的容量来确定,一般通过设置充电桩的台数来反映。
(Ⅲ)交通流量。交通流量是指在确定时间段内通过道路某一地点、某一断面或某一车道的交通实体数,其大小可以判定交通流运行状态。
(Ⅳ)服务半径。参照《城市道路交通规划设计规范》[12]中对城区加油站服务半径的相关规定,同时考虑电动汽车自身的运行特点,服务半径应结合各区域内电动汽车保有量、日均行驶里程和续驶里程等因素进行确定。
(Ⅴ)维护成本。维护成本指保障充电站的正常运营,每年消耗的电动汽车充电站维护成本、充电过程中的损耗成本、电网年损失费用及充电成本等。

表1 电动汽车充电站选址决策评价指标权重
权重大小表征不同指标在充电站选址决策中的地位与作用[13-16]。为消除主观因素的影响,本文运用层次分析法,通过专家调查,计算得到5个电动汽车充电站选址决策评价指标的权重值,如表1所示。
2 充电站选址决策模型
针对充电站选址决策这个模糊不相容问题,建立了电动汽车充电站选址决策模型,采用模糊物元分析理论进行求解。
2.1 模糊物元矩阵构建
事物、特征、模糊量值是模糊物元分析理论用来描述事物的基本元,可表示为:
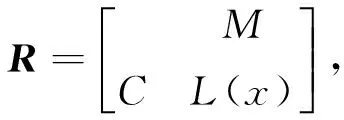
(1)
其中:M为事物;C为事物的特征;L(x)为对应于量值x特征的隶属度。
建立j个比较事物的i维复合模糊物元矩阵,表示为:
(2)
其中:Mj为所比较的事物;Ci为所比较事物的特征;量值L(xji)中j和i分别为所比较事物及相应特征的序号。
2.2 隶属度矩阵变换
引入从优原则实现隶属度矩阵变换,包含以下两种模式。
模式Ⅰ:
ⓐ越大越优。其变换公式为:
(3)
ⓑ越小越优。其变换公式为:
(4)
ⓒ越接近某个常数越优。其变换公式为:
(5)
式(3)~式(5)中:Xji为第j个方案i项指标的量值;Lji为相应指标的从优隶属度;μ0为对应于第i项指标的常数值。
模式Ⅱ:
ⓐ越大越优。其变换公式为:
(6)
ⓑ越小越优。其变换公式为:
(7)
ⓒ越接近某个常数越优。其变换公式为:
(8)
根据电动汽车充电站选址决策评价指标的含义,确定设计规模(C2)、交通流量(C3)、服务半径(C4)这3项指标为越大越优型,建设成本(C1)和维护成本(C5)这两项指标为越小越优型。
观察组患者术后6、12、24、48 h的VAS评分均显著低于对照组同期,差异均有统计学意义(P<0.05),且随时间延长逐渐降低,详见表1。
2.3 求解关联度
关联函数N(x)以x为中间元,与隶属函数L(x)等价。
Nji=Lji,j=1,2,…,m;i=1,2,…,n,
(9)
其中:Nji为第j个方案与标准方案间第i项指标的关联系数。
如上所述,在充电站选址决策关联系数矩阵中,每一个选址方案都有n个关联系数(n=5)。某个充电站备选方案n个关联系数的集中程度用关联度Kj表示;每个充电站备选方案各评价指标的权重用RW表示;各方案的关联度复合模糊物元用RK表示,则有:
RK=RW*RN。
(10)
本文采用M(#,+)运算,所有权重都参与运算,关联度包括所有因素的共同作用,即
(11)
2.4 关联度处理
充电站选址决策的模糊物元分析,需要对求得的关联度进行比较分析以求得最优解,常用最大关联度原则从各个方案的关联度中寻找最大值,即:
K*=max (K1,K2,…,Km),
(12)
其中: K*为对应的选址方案即充电站选址的最优选择。
3 实例分析

表2 环城主干路4个充电站选址备选点评价指标
依据表2中评价指标,建立复合模糊物元矩阵为:
(13)
通过隶属度矩阵变换模式Ⅰ中 3种类型的从优变换,得到隶属度矩阵为:
(14)
把隶属度矩阵Lji作为关联系数Nji,则得关联系数矩阵为:
(15)
所使用的权重复合物元(向量)为:
(16)
采用式(11)计算得到关联度为:
(17)
将关联度按大小排列,有:
K2>K4>K1>K3。
(18)
如式(18)所示,K2所对应的备选点2即为电动汽车充电站选址的最优方案,关联度为8.625。
4 结论
(1)综合考虑充电站的建设成本、交通因素、充电方式和充电站的容量等影响因素,选取充电站的建设成本、设计规模、交通流量、服务半径和维护成本共5个指标,确定了电动汽车充电站选址决策评价指标体系。
(2)应用模糊物元分析理论将充电站选址规划转化为相容问题,从而实现对电动汽车充电站的优化选址。通过对实例的计算和分析,获得了电动汽车充电站选址的最优方案。
[1] 王德荣,王智源,李必鑫.基于模糊物元分析的城市加油站选址决策方法研究[J].重庆科技学院学报(自然科学版),2008,6(3):121-124.
[2] 赵书强,李志伟,党磊.基于城市交通网络信息的电动汽车充电站最优选址和定容[J].电力自动化设备,2016,36(10):8-15.
[3] 吴丽霞,王贝贝,胡静,等.基于熵权模糊物元的电动汽车充电站选址研究[J].公路与汽运,2016(6):45-47.
[4]CLEMENT-NYNSK,HAESENEE,DRIESENJ.Theimpactofchargingplug-inhybridelectricvehiclesonaresidentialdistributiongrid[J].IEEEtransactionsonpowersystems,2010,25(1):371-380.
[5] 王萌,刘凯,牛利勇.电动汽车充电站选址决策与评价研究[J].物流技术,2015,34(18):117-120.
[6] 张港,李明,潘浩,等.市场化的电动汽车充电站规划布局研究[J].陕北电力,2015,43(4):40-44.
[7] 徐坤,周子昂,吴定允,等.电动汽车交流充电桩控制系统设计[J].河南科技大学学报(自然科学版),2016,37(3):47-52.
[8] BRADLEY T,QUINN C.Analysis of plug-in hybrid electric vehicle utility factors[J].Journal of power sources,2010,195(16):5399-5408.
[9] 周文峰,李珍萍,崔晓洁,等.电动汽车充电站选址问题研究[J].数学的实践与认识,2016,46(11):187-194.
[10] SATHAYE N,KELLEY S.An approach for the optimal planning of electric vehicle infrastructure for highway corridors[J].Transportation research part e,2013,59:15-33.
[11] 所丽,唐巍,白牧可.考虑削峰填谷的配电网集中型充电站选址定容规划[J].中国电机工程学报,2014,34(7):1052-1060.
[12] 中华人民共和国建设部.城市道路交通规划设计规范:GB 50220—95[S].北京:中国计划出版社,1995.
[13] 王辉,王贵斌,赵俊华,等.考虑交通网络流量的电动汽车充电站规划[J].电力系统自动化,2013,37(13):63-69.
[14] 邵赛,关伟,毕军.考虑排队时间和里程约束的竞争充电站选址问题[J].交通运输系统工程与信息,2016,16(6):169-175.
[15] 杨佳俊,陈红,段美琪,等.电动汽车充电站多阶段规划研究[J].山东电力技术,2015,42(8):18-22.
[16] 杨波,陈卫,文明浩,等.电动汽车充电站的概率负荷建模[J].电力系统自动化,2014,38(16):67-73.
国家自然科学基金项目(51605265,51508315);山东省自然科学基金项目(ZR2014EL036,ZR2015PE020)
郑春燕(1983-),女,山东德州人,讲师,硕士,主要从事充电站选址决策等方面的研究.
2016-12-30
1672-6871(2017)04-0039-04
10.15926/j.cnki.issn1672-6871.2017.04.009
U469.7
A
