时间尺度上非完整系统的Noether准对称性与守恒量

金世欣,李莉,李彦敏

(1.商丘师范学院 数学与统计学院,河南 商丘 476000;2.商丘师范学院 电子电气工程学院,河南 商丘 476000)

时间尺度是实数集上的任意非空闭子集.时间尺度上力学系统动力学理论统一和拓展了连续和离散力学系统理论,不仅能够揭示连续和离散系统动力学之间的差别与联系,而且更准确地刻画复杂动力学系统的本质,有效地避免了出现差分方程和微分方程这两种结果[1].考虑时间尺度的影响,研究非完整系统动力学特性,不仅可以更深入认识系统本身,而且对相关领域的研究起到促进作用.时间尺度上的微积分理论是由Hilger引入[2],其思想是统一和拓展连续和离散理论分析,其目的是将微分和差分理论融合一起进行研究,分析它们之间的区别与联系,避免了许多连续和离散问题的重复工作,同时也为研究微分和差分提供强有力的理论依据.近年来,随着时间尺度理论的发展和完善,使得时间尺度理论在科学和工程的很多领域(如数学,最优控制学,物理学,经济学,力学等)得到越来越广泛应用[3-7].

2004年Bohner[8]、Hilscher和Zeidan[9]讨论了时间尺度上动力学系统的变分问题.关于时间尺度上动力学系统的Noether守恒量有两种类型.第一种类型是Bartosiewicz和Torres[10]建立的时间尺度上动力学系统的Noether定理,并利用时间重新参数法给出了Noether定理的证明.此后,Bartosiewicz[11,12]等建立了时间尺度上动力学系统的第二Euler-Lagrange方程,并基于第二Euler-Lagrange方程给出了时间尺度上Noether定理的另一证明方法.近年来,在Bartosiewicz和Torres等研究工作的基础上,关于时间尺度上动力学系统的Noether对称性与守恒量理论问题得到了进一步的完善和发展[13-24].第二种类型是Cresson[25]团队提出的时间尺度上动力学系统的Noether型定理,并用直接法给出了时间尺度上Noether定理的证明.zhɑng[26,27]等给出并证明了时间尺度上完整非保守力学系统的Noether定理,揭示了时间尺度上Noether对称性与守恒量之间的联系,并推广到了分数阶时间尺度上的Noether定理,给出了时间尺度上分数阶Noether守恒量的数值分析,并进一步讨论了时间尺度上广义Chaplygin系统的摄动与绝热不变量和时间尺度上非迁移动力学系统的Mei对称性[28,29].本文基于Cresson 团队和zhɑng的工作,进一步研究时间尺度上非完整系统的Noether准对称性与守恒量,将时间尺度上Noether对称性方法应用于时间尺度上非完整系统,分别基于时间尺度上Birkhoff框架、Lagrange框架和Hamilton框架,建立时间尺度上Noether准对称性和Noether等式,并用直接法证明时间尺度上的Noether守恒量.

1 时间尺度上Lagrange框架下的Noether守恒量

设在时间尺度上Lagrange框架下,时间尺度上非完整系统动力学方程可化为相应的时间尺度上一般完整系统的Lagrange方程

(1)

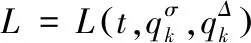
引入时间变换的无限小群变换

(2)

其中,ξ0,ξs是生成元.

于是,有

(3)

则该系统存在如下形式的时间尺度上的Noether守恒量

(4)

证明 将式(4)两边对t同时求Δ导数,并利用式(3)和方程(1),可得

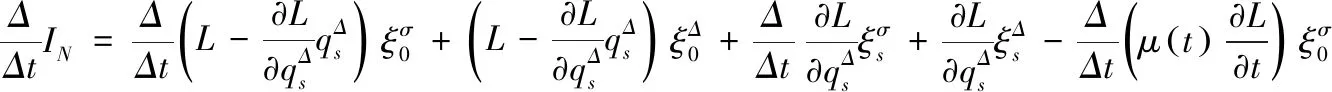
(5)

因此,式(4)是时间尺度上Lagrange框架下的Noether守恒量.

2 时间尺度上Hamilton框架下的Noether守恒量

若令

(6)

则时间尺度上Lagrange框架下的动力学系统就化为了时间尺度上Hamilton框架下的动力学系统.则时间尺度上非完整系统动力学方程可化为时间尺度上相空间中一般完整系统的Hamilton方程,有

(7)

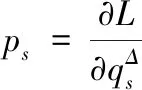
引入时间变换的无限小群变换

(8)

其中,ξ0,ξs和ηs是生成元.

于是,有

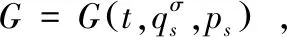
(9)

则该系统存在如下形式的时间尺度上的Noether守恒量

(10)

证明 将式(10)两边对t同时求Δ导数,并利用式(9)和方程(7),可得

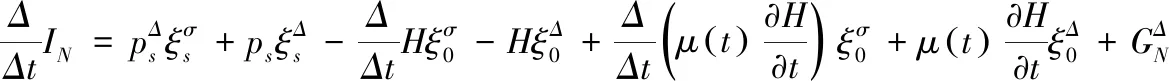
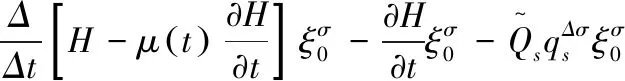
(11)

故式(10)是无限小群变换(8)下的时间尺度上Hamilton框架下的Noether守恒量.

3 时间尺度上Birkhoff框架下的Noether守恒量

若取

(12)

则时间尺度上Hamilton框架下动力学系统为时间尺度上Birkhoff框架下的动力学系统特例.则时间尺度上非完整系统动力学方程可化为相应时间尺度上广义Birkhoff方程,有

(13)

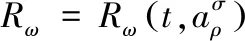
引入时间变换的无限小群变换

(14)

其中,ξ0,ξs是生成元.

于是,有

(15)

则该系统存在如下形式的时间尺度上的Noether守恒量

(16)

证明 将式(16)两边对t同时求Δ导数,并利用式(15)和方程(13),可得

(17)

因此,式(16)是时间尺度上Birkhoff框架下的Noether守恒量.

4 讨 论

若T=P,则σ(t)=t,μ(t)=0,则时间尺度上非完整系统相应完整系统运动微分方程(1),(7)和(13)就成为[30,31]

(18)

(19)

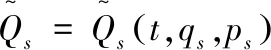
(20)

其中Rω=Rω(t,aρ)是Birkhoff函数组,B=B(t,aρ)是Birkhoff函数,Λω=Λω(t,aρ)为附加项.

定理1、定理2和定理3就成为:

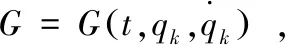
(21)

则该系统存在如下形式的Noether守恒量

(22)

推论2对于非完整系统相应完整系统(19),如果无限小群变换下的生成元和规范函数G=G(t,qs,ps),满足如下等式

(23)

则该系统存在如下形式的Noether守恒量

IN=psξs-Hξ0+GN=const.

(24)

推论3对于非完整系统相应完整系统(20),如果无限小群变换下的生成元和规范函数G=G(t,aω),满足如下等式

(25)

则该系统存在如下形式的Noether守恒量

IN=Rωξω-Bξ0+GN=const.

(26)

若T=hZ时,σ(t)=t+h,μ(t)=h,则时间尺度上非完整系统相应完整系统运动微分方程(1),(7)和(13)就成为

(27)

其中,L=L(t,qs(t+h),Δtqs)为离散Lagrange函数,Qs=Qs(t,qs(t+h),Δtqs)为非势广义力.

(28)

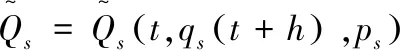
(29)

其中,Rω=Rω(t,av(t+h))是Birkhoff函数组,B=B(t,av(t+h))是Birkhoff函数,Λω=Λω(t,av(t+h))为附加项.

定理1、定理2和定理3就成为:

推论4对于非完整系统相应完整系统(27),如果无限小群变换下的生成元和规范函数G=G(t,qk(t+h),Δtqk),满足如下等式

Qs(ξs(t+h)-Δtqs(t+h)ξ0(t+h))+ΔtGN=0

(30)

则该系统存在如下形式的离散Noether守恒量

(31)

推论5对于非完整系统相应完整系统(28),如果无限小群变换下的生成元和规范函数G=G(t,qs(t+h),ps),满足如下等式

(32)

则该系统存在如下形式的离散Noether守恒量

IN=psξs-Hξ0+GN=const.

(33)

推论6对于非完整系统相应完整系统(29),如果无限小群变换下的生成元和规范函数G=G(t,aω(t+h)),满足如下等式

BΔtξ0+Λυ(ξυ(t+h)-Δtaυ(t+h)ξ0(t+h))+ΔtGN=0

(34)

则该系统存在如下形式的离散Noether守恒量

IN=Rωξω-Bξ0+GN=const.

(35)

5 例 题

例1时间尺度上匀质圆球纯滚动问题.时间尺度上动力学系统的Lagrange函数为

(36)

系统所受约束为

(37)

试讨论该系统的Noether对称性与守恒量.

相应完整系统的Lagrange函数和非势广义力为

(38)

(39)

由式(3),可得

(40)

方程(40)有解

ξ0=0,ξ1=1,ξ2=ξ3=0,G=0

(41)

由式(4),得到守恒量

(42)

若T=P时,则σ(t)=t,μ(t)=0,则守恒量(42)就成为

(43)

若T=hZ时,σ(t)=t+h,μ(t)=h,则守恒量(42)就成为

(44)

例2时间尺度上Duffing方程为

qΔΔ+qσ+(qσ)3=0

(45)

试讨论该系统时间尺度上Noether对称性与守恒量.

方程(45)可化为相空间中一般完整系统的时间尺度上Hamilton方程,有

(46)

由式(9),可得

(47)

方程(47)有解

ξ0=0,ξ=1,G=-qΔ

(48)

由式(10)可得

I=p-qΔ=const.

(49)

例3时间尺度上非线性耦合振子方程为

(50)

其中,ω1,ω2和α为常数,试研究该系统时间尺度上Noether对称性与守恒量.

令

a1=x,a2=y,a3=xΔ,a4=yΔ

(51)

方程(50)可化为时间尺度上广义Birkhoff方程,有

(52)

由式(15),可得

(52)

方程(52)有解

(53)

由式(16)可得系统的守恒量为

(54)

6 结 论

文章通过分析时间尺度上Noether准对称讨论时间尺度上非完整系统的Noether准对称性及其守恒量.基于时间尺度上Lagrange框架、Hamilton框架和Birkhoff框架,将非完整系统动力学方程转化为相应一般完整系统的运动微分方程,建立了无限小群变换下的时间尺度上Noether准对称性和广义Noether等式,给出并用直接法证明了时间尺度上的Noether守恒量(定理1-定理3).结果表明:时间尺度上Lagrange框架下的Noether守恒量与时间尺度上Hamilton框架下的Noether守恒量等价,而时间尺度上Hamilton框架下的Noether守恒量是时间尺度上Birkhoff框架下的Noether守恒量的特例.当T=P时,时间尺度上Noether守恒量就成为了经典动力学系统的Noether守恒量(推论1-推论3).当T=hZ时,时间尺度上Noether守恒量就成为离散动力学系统的Noether守恒量(推论4-推论6).本文的方法和结果具有普遍性,可进一步推广应用于含有两个及以上小参数的或含有多个独立变量的时间尺度上非完整动力学系统、时间尺度上的最优控制系统等.