数列求和裂项相消问题 临高考前答学生问

武增明 (邮编：653100)

云南省玉溪第一中学

数列求和裂项相消问题 临高考前答学生问

武增明 (邮编：653100)

云南省玉溪第一中学

距离高考仅有一个半月，一位高三的学生焦急地问笔者这样一个问题：“老师，我对数列求和裂项相消问题不熟，有些生疏，有没有考前临时抱佛脚的方法.”这是一个很棘手的问题，作为老师的我不能在临近高考之时打击学生的信心.笔者第二天给了学生如下文章，不是很全面，也许不妥当，权当临时抱佛脚.现送给每一位考生，希望能够抚平焦虑的考生.

1 积累基本裂项模型

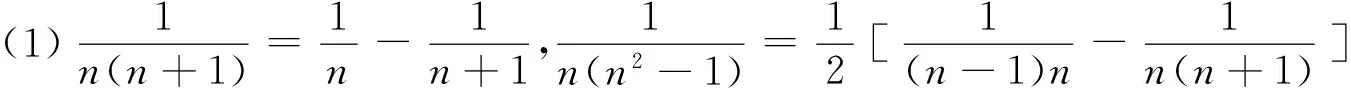
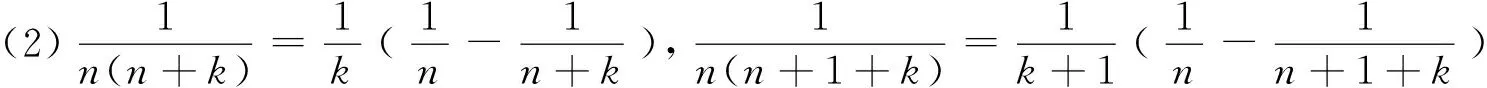
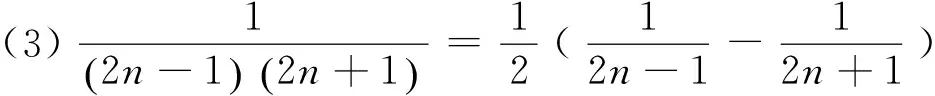
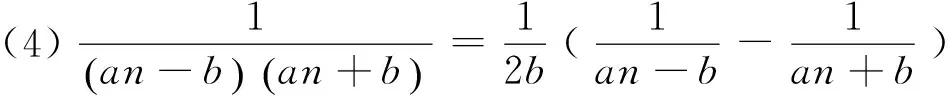
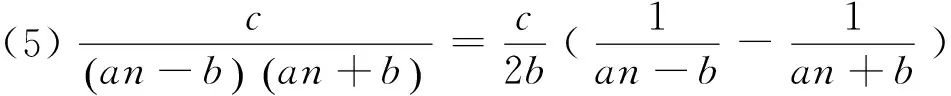
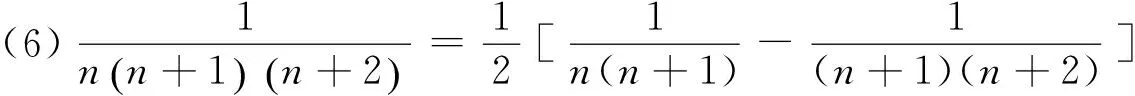
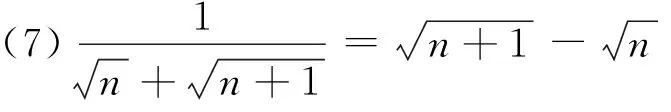
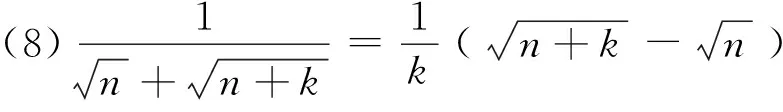
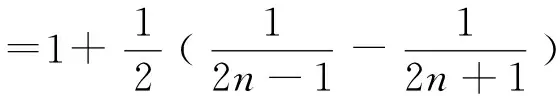
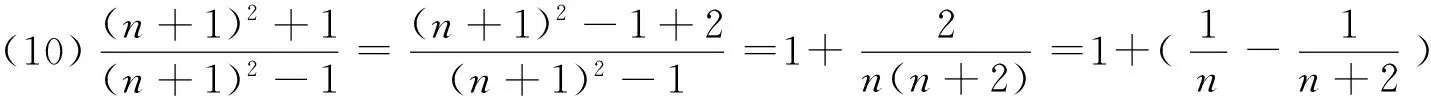
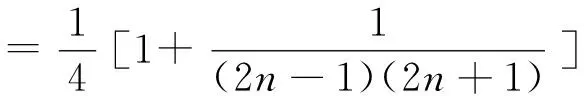
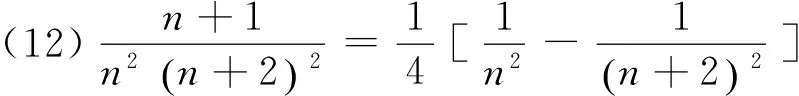
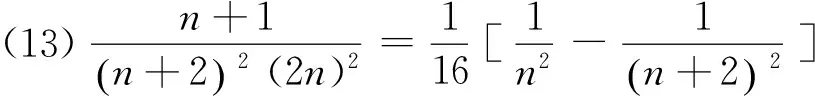
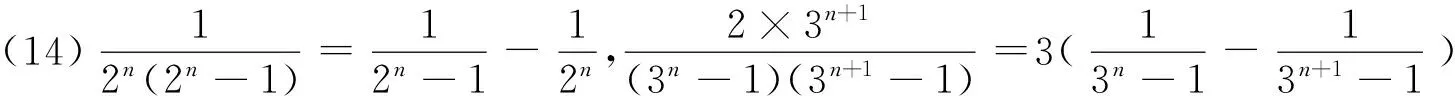
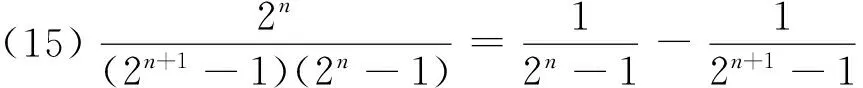
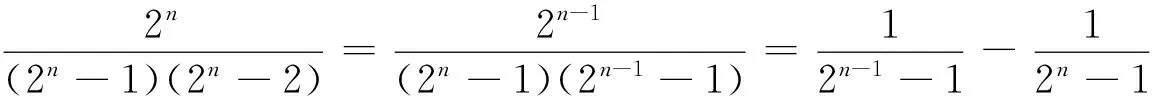
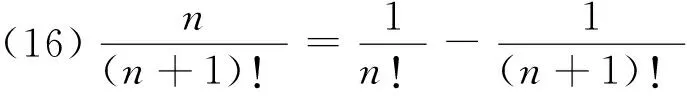
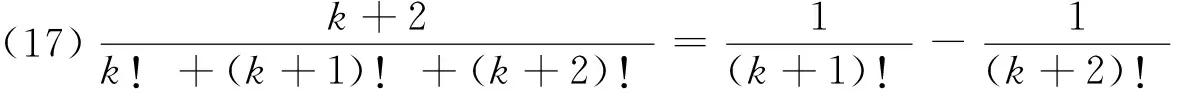
(18)n·n!=(n+1)!-n!.

2 掌握两个重要裂项模型

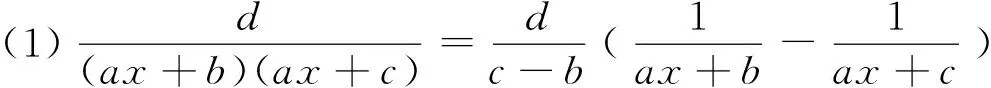
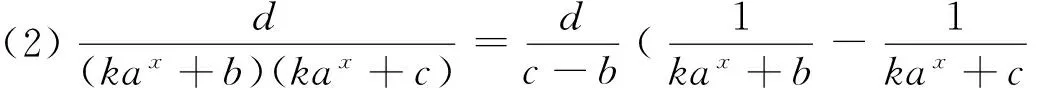
3 清楚一个裂项思路

把数列通项凑出两个数列通项之差，且求和时能消掉多数项.

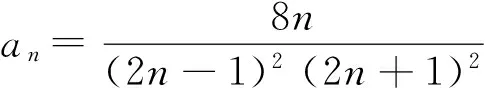
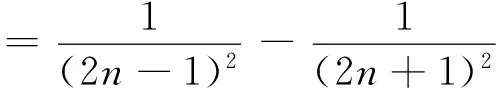
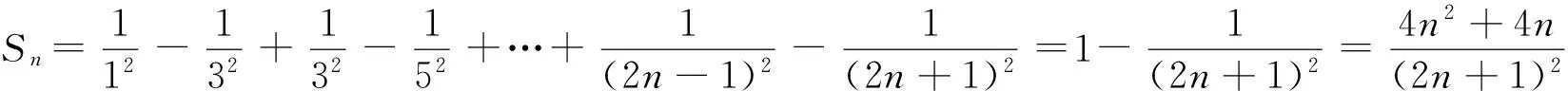
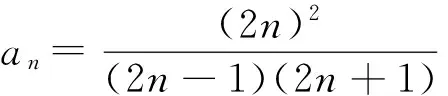
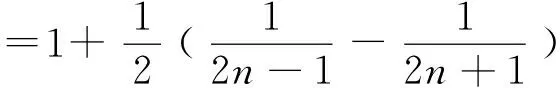
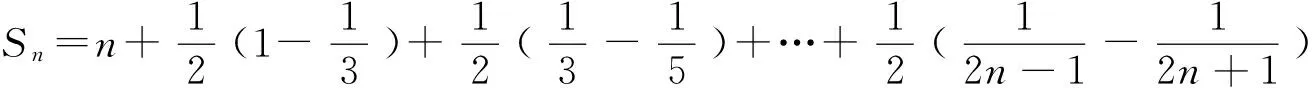
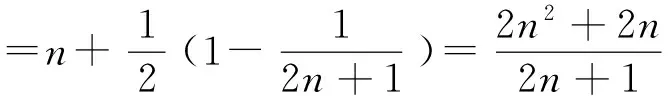
例3 已知数列{an}的前n项和为Sn，Sn=2an+n.

(Ⅰ)求数列{an}的通项公式an；

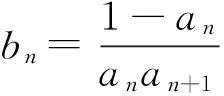
解 (Ⅰ)略，an=1-2n.

(Ⅱ)由(Ⅰ)知，an=1-2n，

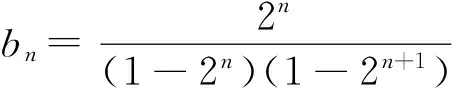
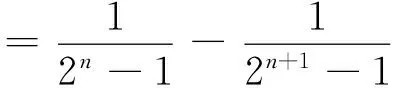
所以Tn=b1+b2+…+bn

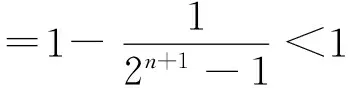
从而Tn<1.

2017-01-09)