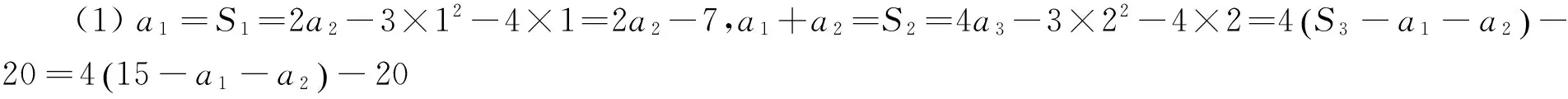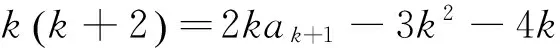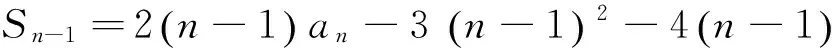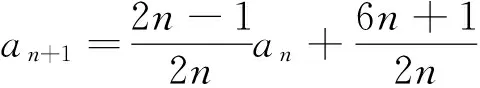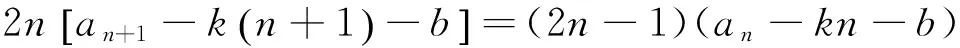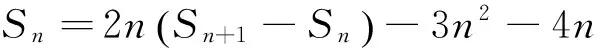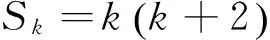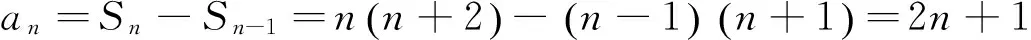错在哪里
2017-04-24佟彦泽,查正开,王荣峰
数 学 园 地
错在哪里
1 江苏省海州高级中学
佟彦泽 (邮编:222062)

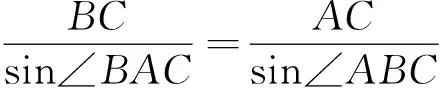
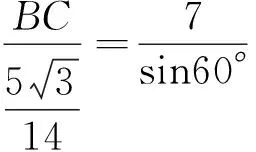
由余弦定理得BC2=AB2+AC2-2AB·ACcos∠BAC,
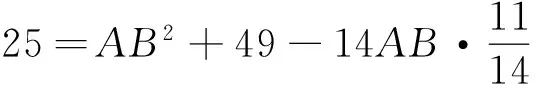
解得AB=3或AB=8.
解答错了!错在哪里?
由以上错解可知∠BAC只有一解,又因为∠ABC=60°,所以∠ACB也是唯一确定,再由AC=7可以知道△ABC是唯一确定的,所以错解中产生了一个增解.错解的补救措施是验证:若AB=3,则AC2>AB2+BC2,∠ABC为钝角,实际此时∠ABC=120°,不合题意;若AB=8,经检验符合题意.

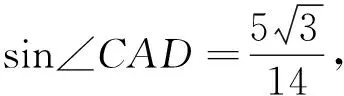
sin∠ACB=sin(∠ABC+∠BAC)=sin(60°+∠BAC)
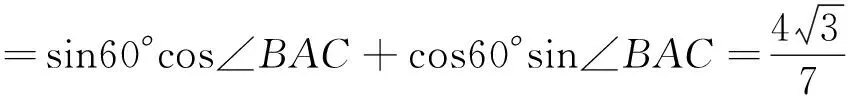

正解2 同错解得BC=5.
由余弦定理得AC2=AB2+BC2-2AB·BCcos∠ABC,
即49=AB2+25-5AB,即AB2-5AB-24=0,
解得AB=-3(舍去)或AB=8.
变式1 在△ABC中,已知∠ABC=60°,AC=7,BC=5,求AB的长.
解 由余弦定理得AC2=AB2+BC2-2AB·BCcos∠ABC,
即49=AB2+25-5AB,即AB2-5AB-24=0,
解得AB=-3(舍去)或AB=8.

解 由余弦定理得BC2=AB2+AC2-2AB·ACcos∠BAC,
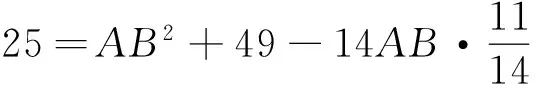
解得AB=3或AB=8.
由此可以得出:在三角形中,如果已知大边对大角和一条小边,运用余弦定理求得第三条边只有一解(有一个负数解自然舍去);如果已知小边对小角和一条大边,运用余弦定理求得第三条边则有两解(不要舍去).而题目的错解就是因为在△ABC中,同时已知大边对大角和知小边对小角,应该是变式1的类型,却错误地当作变式2的类型求解导致产生增解,使解题出现偏差.
2 江苏省常熟市中学
查正开 (邮编:215500)
题目 (《数学通讯》2017年第1期数学问题征解题281)
设a、b、c为非负实数,且a+b+c=1,求P=a3+b3+c3-a4-b4-c4的最大值.
先给出如下解答:
t=a4+b4+c4 本文只是粗浅地讨论了研究区域内房价偏离与“补涨”效应可能的联系,并没有对“补涨”的作用强度和滞后时间进行精确的量化,这有待今后进一步研究。 解答错了?错在哪里? P=a3+b3+c3-a4-b4-c4的最大值,并不等价.这与运用基本不等式求最值时要确保放缩后必须是定值的原因是一样的,在应用不等式处理最值问题是应该杜绝这样的错误. 下面给出这个问题的一个正确解法,供读者参考. 正解 由于a,b,c为非负实数,且a+b+c=1,因此 P=a3+b3+c3-a4-b4-c4 b+c) 当且仅当abc=0,a2+b2+c2=2ab+2bc+2ca时,上式取到等号. 王荣峰 (邮编:158100) (1)求a1、a2、a3的值; 该题为江苏省运河高等师范学校许荣良老师发表在《中学数学》2016年第12期的论文《数学归纳法中运用归纳假设的策略》中的例2,它也是2014年全国高考广东省理科试卷的第19题. 对于(2) 由(1)猜想an=2n+1,以下用数学归纳法证明: 1.由(1)知,当n=1时,a1=3=2×1+1,猜想成立; 综合①②可知对一切n∈N*,an=2n+1成立. 解答错了!错在哪里? 高考的参考答案也是如上给出的,证明过程看似合情入理,无懈可击,但笔者认为是有问题的!准确应用归纳假设是用数学归纳法解题的关键,而在(2)的证明过程中, 对假设的应用是不正确的,第二步归纳假设的只是当n=k时才有猜想ak=2k+1成立,而对未经验证和未假设的第m(4≤m≤k-1,m∈N*)项,却不可写成am=2m+1. 正解 1由(1)易知,当n=1和n=2时,猜想成立; 综合①②可知对一切n∈N*,an=2n+1成立. 评注 借助公式an=Sn-Sn-1(n≥2,n∈N*)挖掘到an+1与an的递推关系,为用数学归纳法顺证该题创造了条件. 别解1 待定系数 别解2 先求出Sn 证明: (1)显然当n=1时,猜想成立; 学习实践证明,对一些典型的易错题进行辨析和总结,不但可以提高解题的准确率, 加深对相关知识的理解,同时更有利于形成缜密的和善于批判的思维品质.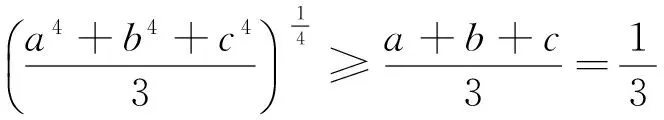
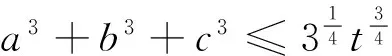
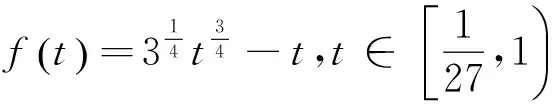
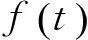

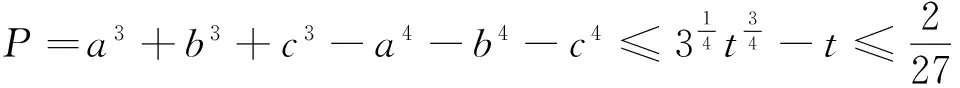
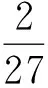
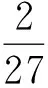

3 黑龙江省鸡西市第一中学