例谈高中数学“易错题”的教学价值
2017-04-24邮编246000
邵 安 (邮编:246000)
安徽省安庆市第二中学(本部)
例谈高中数学“易错题”的教学价值
邵 安 (邮编:246000)
安徽省安庆市第二中学(本部)
大多教师都有这样的感受:学生对某些数学题做了又做,重复地做了以后再次遇到还是做错了.仔细研究,发现他们做错的题大部分属于数学中的“易错题”,这种反复做错的现象显然不是有效教学.有效教学[1]指教师遵循教学活动的客观规律,以最少的时间、精力和物力投入,取得尽可能多的教学效果.作为教师,都知道解一道有代表性的题可以让学生掌握解其他题的思路与方法,因此教师在教学中应高度重视“易错题”的示范作用,通过将“易错题”作为典例,既能教会学生分析解答错误的原因,又可使学生加深对错题的印象,减少错误再犯的概率,进而达到触类旁通,事半功倍的效果.本文对用“易错题”作为范例讲解的必要性、高中数学中学生求解“易错题”出错的主要原因、“易错题”的教学价值等,做出了相应的分析思考.根据自身的教学实践,在教学中合理采取“易错题”作为范例,充分发挥“易错题”的教学价值,呈现的教学效果表明这种做法是很好的.
1 用“易错题”作为范例讲解的必要性
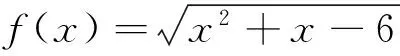

错误类型答对忽略定义域计算失误不会做错误人数1962117所占比例19.19%62.63%11.11%7.07%
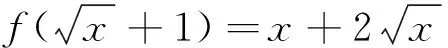
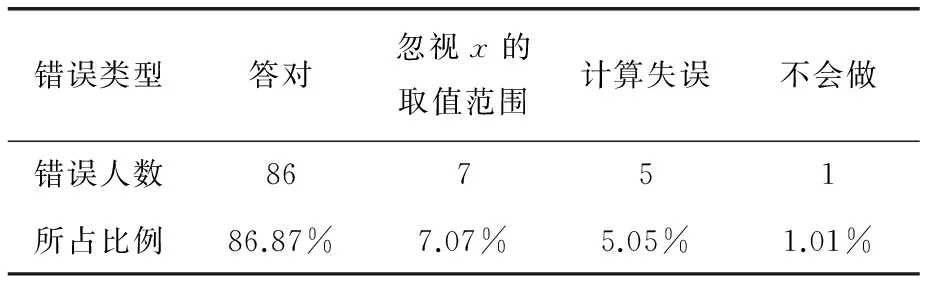
错误类型答对忽视x的取值范围计算失误不会做错误人数86751所占比例86.87%7.07%5.05%1.01%
由此可见“易错题”的教学价值之重要,课堂上选择“易错题”作为范例讲解,虽然学生在开始解答的过程中容易出现错误、暴露问题,往往这样暂时的错误与问题会给学生带来永久的记忆.而这些错误和问题正好可以作为教师指出错误的“典型例题”,帮助学生透彻地分析出错的原因,并及时地纠错,帮助学生将缺失的知识或能力补上.这样不仅使学生加深了错题的印象,避免下次再犯同一类型的错误,而且帮助学生分析了出错的根本原因,如此的过程为学生今后能更加完美地解题提供思路,帮助学生养成良好的思考习惯.
2 学生求解“易错题”出错的主要原因
学生在求解“易错题”时出错的原因有很多,因为不同的学生对知识掌握的程度不同,具备的能力也不尽相同.出错的原因看似错综复杂,但根据题目本身的特征,从出题的角度,可以总结出导致学生出错的规律,现将学生解题易错的主要原因归纳为下面的五个方面.
2.1 审题不清
例1 若函数f(x)=x2-2ax+2在区间[0,4]上至少有一个零点,求实数a的取值范围.
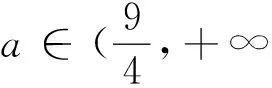
正解 因为函数f(x)=x2-2ax+2在区间[0,4]上至少有一个零点,且f(0)=2>0,所以
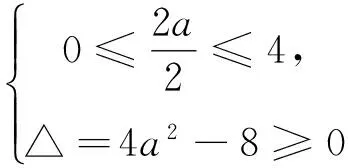
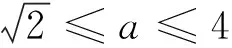
例2 某厂两年内产值的月增长率都是a,则这两年内第二年某月的产值比第一年相应月的产值增长了多少?
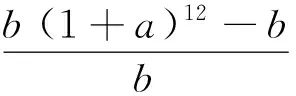
错解 没有看清题目中所跨过的时间间隔数,从而得出错误答案:增长了(1+a)11-1.
2.2 混淆概念
例3 若函数f(x)=x2+2(a-1)x+1的单调递减区间是(-∞,1],则实数a的取值范围为______.
错解 本题易错地方是将函数f(x)的单调递减区间为(-∞,1]误理解为在区间(-∞,1]上单调递减,于是由二次函数的图象得1-a≥1,所以a≤0.“单调区间”与“区间上单调”是完全不同的两个概念,应悉心体会、准确把握.
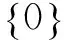
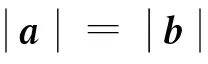
A.0个B.1个C.2个D.3个
错解 容易错选D.导致错误的原因如下:①忽略了0和0的区别,应为a=0;
②混淆了两个向量的模相等和两个实数相等,两个向量的模相等,只能说明它们的长度相等,它们的方向并不确定;③两个向量平行,可以得出它们的方向相同或相反,未必得到它们的模相等;④当b=0时,a、c可以为任意向量,故a不一定平行于c.
正解 由上面的分析可知,4个命题均错误,故选A.
2.3 考虑问题不全面


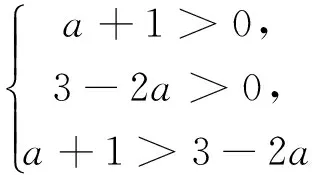
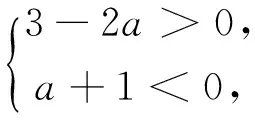
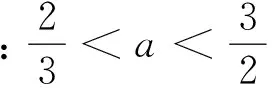
例6 求半径为4,与圆C:x2+y2-4x-2y-4=0相切,且和直线y=0相切的圆的方程.
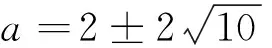
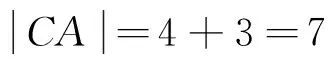
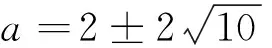
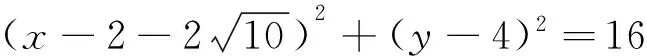
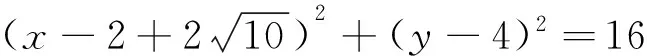
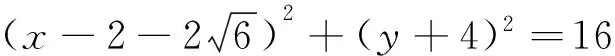
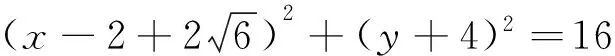
2.4 忽视隐含条件
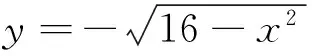
错解 以(0,0)为圆心,半径为4的圆.忽视了隐含条件:y≤0.
正解 以(0,0)为圆心,半径为4的半个圆.
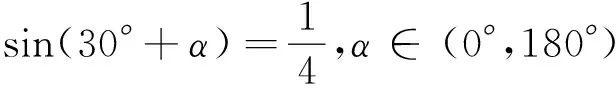
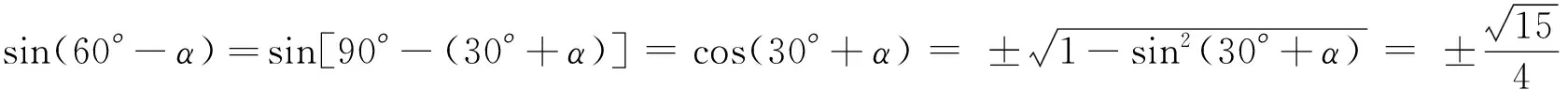
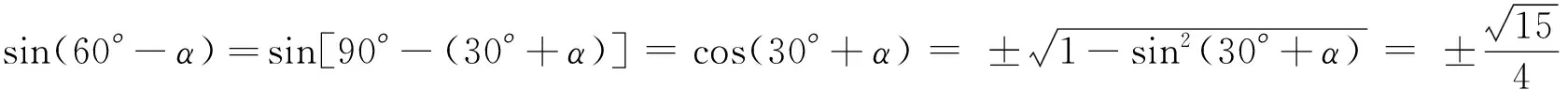
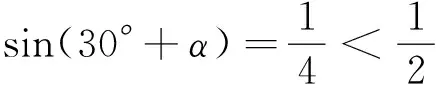
2.5 忽视实际意义
错解 由已知得:
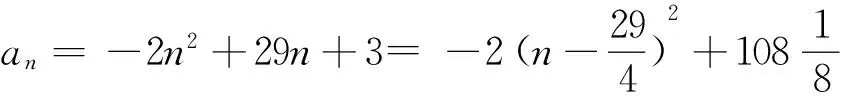
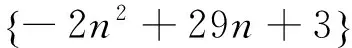
数列是一个特殊的函数,在应用函数的有关知识求解数列问题时,要注意它的实际意义,即n∈N*这一约束条件.
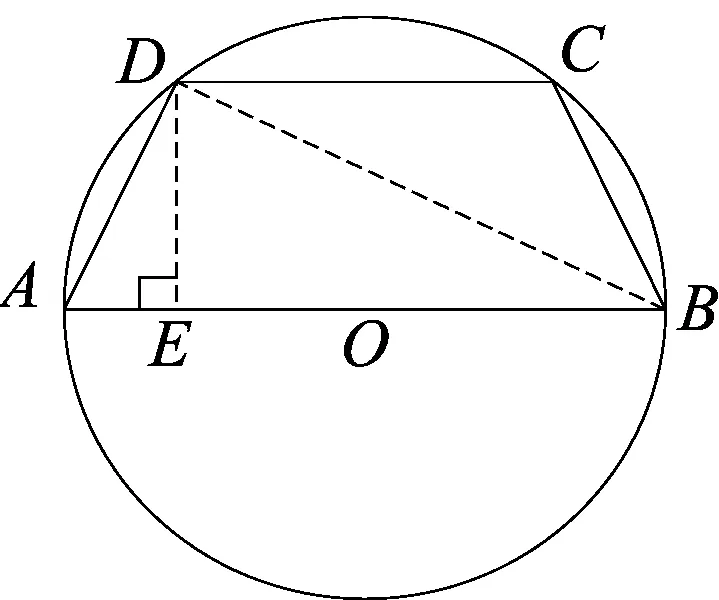
图10
例10 如右图所示,半径为R的圆的内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆上,写出这个梯形的周长y与腰长x之间的函数关系式,并求出其定义域.
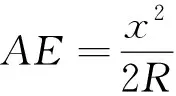
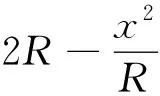
2.6 知识点掌握不牢固
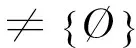
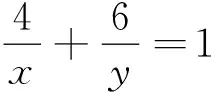
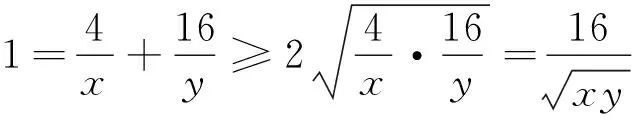
3 “易错题”的教学价值
通过以上分析可以看出,高中数学“易错题”的教学价值是显而易见的,教师如果认真面对学生遇到的这些“易错题”,帮助学生仔细剖析出错的原因,并给予强化训练,那么“易错题”的教学价值便能很快地体现出来:讲好“易错题”既能帮助学生意识到解题要注意审题,考虑问题要全面,深刻理解知识点、概念,提醒学生解题不要忽视隐含条件、实际意义等;而《课程标准》明确指出[3],课程的基本理念之一是注重提高学生的数学思维能力,所以,讲好“易错题”又是培养学生的思维创造性、深刻性和严密性的必然途径.
那么,教师在日常的教学实践中,如何利用这些“易错题”呢?一、收集“易错题”,形成错题集;二、认真上好每一节错题分析课并强化训练;三、针对每个易错点,不定期地进行考试检测并适当地进行奖罚.总之,“易错题”就像是一副“良药”,上好错题分析课就是“对症下药”,充分挖掘“易错题”的教学价值,激发学生的学习兴趣,培养学生勇于探索的精神,对学生思维能力的训练和综合素质的全面提高,都有着举足轻重的作用.
1 李长娟. 师德践行课堂案例读本--师德修养[M]. 北京:世界图书出版公司,2015(6)
2 田立君. 学习评价的理论与应用[M]. 长春:东北师范大学出版社,2015(4)
3 中华人民共和国教育部制订. 普通高中数学课程标准(实验)[M]. 北京:人民教育出版社,2015(7)
2017-01-06)
