基于群智能算法的神经网络建模研究

王闪闪

(上海理工大学 光电信息与计算机工程学院，上海200093)

基于群智能算法的神经网络建模研究

王闪闪

(上海理工大学 光电信息与计算机工程学院，上海200093)

针对神经网络建模过程中不合理的权值选取，使训练陷入局部最优解而得不到全局最优解这一问题。采用群智能算法得出全局最优解，并且利用检验样本达到最低点时的权值与阈值正确建立神经网络模型。结果表明，网络模型的评价参数表现良好，其中预测精度与相关系数分别为97.55%和96.2%。从而证明了基于群智能算法的神经网络，在遵循建模条件情况下能够保证取得全局最优解，建立的模型性能良好，具有一定的理论与市场应用价值。

神经网络；群智能算法；全局最优解；优异性能

人工神经网络以其较强的自学习、自组织、较好的容错性和优良的线性逼近能力，采用误差反传算法或其变化形式的神经网络模型在很多领域得到了良好的应用[1]，如农作物的生产、价格的预测以及各种生物药剂的制造、基因的研究等方面，合理应用神经网络模型能够提高药物产量、节约时间、降低成本、减少人力物力财力的浪费从而提高效率。

神经网络建模必须遵循建模条件[2]，此外神经网络模型训练中最重要的就是寻找最优的权值[3]，只有通过不断改变最初的权值找出最优的权值和阈值，才能保证训练出来的网络具有很强的优异性能、线性逼近能力等优点[4]。针对这一问题，本文利用群智能与神经网络相结合的方法，通过群智能算法[5]计算出最优的权值和阈值,然后利用最优的权值和阈值建立神经网络模型。

1 神经网络建模原理

1.1 神经网络建模条件

正确合理的利用神经网络建模能够使得神经网络模型具有很好的效果。而不正确的建立神经网络模型会导致很多问题：(1)网络结构过大或过小都会造成过拟合或者欠拟合。随着隐层节点数的增多，误差减小会导致网络结构过大，从而使得训练过程中出现过拟合现象；(2)训练样本、测试样本以及检验样本的缺失或者选取不合理都有可能使得建立的神经网络模型失去泛化能力；(3)初始权值的不合理选取使得训练进入局部极小点。

因此正确了解神经网络建模条件才能更好的应用于需求中。建立正确的BP神经网络模型需要满足的条件：(1)隐层以及节点数与很多因素有关，应该取尽量少的隐层数目，此外隐层节点数的选取应该通过试凑法选取而不是公式法，因为公式法只针对特定情况满足，而且多数是不利的情况不宜采用[6]；(2)在满足精度的前提下，取尽可能少的隐层以及隐层节点数；(3)检验样本监控训练过程，避免出现过训练现象；(4)一般情况下，要求训练样本数至少要多于网络连接权值数，同为2～10倍。样本量比较少时，可以采用轮训的方法；(5)对于一定的网络结构，应通过不断改变网络连接权值的初始值，通过比较系统误差值的大小确定全局最优值。

1.2 粒子群算法

粒子群算法(PSO)是一种新兴的演化计算技术，PSO最早是在1995年由Eberhart和Kennedey共同提出的，可以有效的优化各种函数，此算法依赖于随机的过程，还使用了适应值的概念[7]。将此算法应用到网络权值的训练上,可以得出全局最优解。PSO简单容易实现并且没有许多参数需要调整等优势，目前已经广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。此外速度更新公式为

(1)

1.3 指标评价函数

使用误差评价函数来预测效果的好坏，其中设i为数据序号;数据个数为N，Pi为预测数值;Pm为预测的均值;Oi为观测数据值;Om为预测数据的平均值;Sp为预测数据的标准差;So为观测值的标准差[8]。

(1)均方根误差，反映了预测值对观测值的平均偏离程度，取值大于或等于零，预测无误差时等于零

(2)

(2)偏差，反映预测值对观测值的平均系统性的偏离

(3)

(3)预测精度EPA，反映了预测值与其平均值的偏差与观测值周围偏离程度之间的相关性。值为1时表明预测与实际数据分别对自身的均值和标准差归一化后是相同的，当值为1时代表预测完全无误差

(4)

(4)决定度系数。反映预测数据对观测数据值均值的偏离程度

(5)

2 实例与分析

2.1 数据来源

以文献[9]为例，数据表如表1所示，其中x1、x2、x3分别为BFSH、时间和pH。Y为乙醇产量，其中BFSH为一种用于乙醇生产和发酵参数优化的碳源。文献中样本量为17组，采用的神经网络结构为3-3-1，计算神经网络结构的权值数为18，样本数据少于神经网络权重数量，可判断神经网络结构过大。按文中方法进行训练得到结果如图1和图2所示。

2.2 正确建立神经网络模型

由于神经网络对样本量比较大且具有代表性的数据优化能力较好，而对样本量比较小的数据的拟合能力较差，所以通过增加噪音的方法扩充样本量[10]，对17组样本进行扩充，扩充后样本量为102个，通过试凑法选取隐层节点数为8，在遵循神经网络建模条件的情况下进行建模，群智能算法迭代出每次迭代中的全局最优解，利用检验样本实时监控整个训练过程，在检验样本出现过训练即达到最低点有增加的趋势时，取最低点时的权值与阈值，建立神经网络模型。训练过程如图3与图4所示，结果分析如表2所示。

2.3 结果分析与讨论

利用神经网络技术对实验数据进行建模时候必须遵循建模条件，文献[11～16]中均没有检验样本监控训练过程，因此训练过程中可能会出现过训练现象，并且无法选取最优的权值和阈值，也就无法保证能够求得全局最优解，严重影响了模型的可靠性。文献[9]中数据训练得出的神经网络模型泛化能力差，因此模型不具备良好的可靠性，依据此模型训练出来的结果也是不可靠的。通过图1可以看出，训练过程中出现过训练现象，并且最终训练样本、测试以及检验样本的误差相差较大，因此模型并没有理想的泛化能力。同时文中仅通过判断误差<0.001来确定是否达到期望结果是不可行的，因为仅通过不断增加隐层数目，误差也会逐步减少达到理想的效果，甚至可以趋近于0，但训练过程中会出现过训练现象，模型性能并不可靠。图3以及图4为在遵循建模条件下，并且利用群智能算法求出全局最优解。通过图3可知，训练过程没有发生过训练现象，最终训练、测试以及检验样本的误差相差很近，基本趋于同一条直线，说明模型具有良好的泛化能力。通过结果分析表2可知，模型的预测精度以及相关系数较高分别为97.55%、96.2%。同时均方根误差以及偏差都比较小，均方根误差以及偏差均比较小，表明模型具有良好的参数优化效果。

表1 数据表

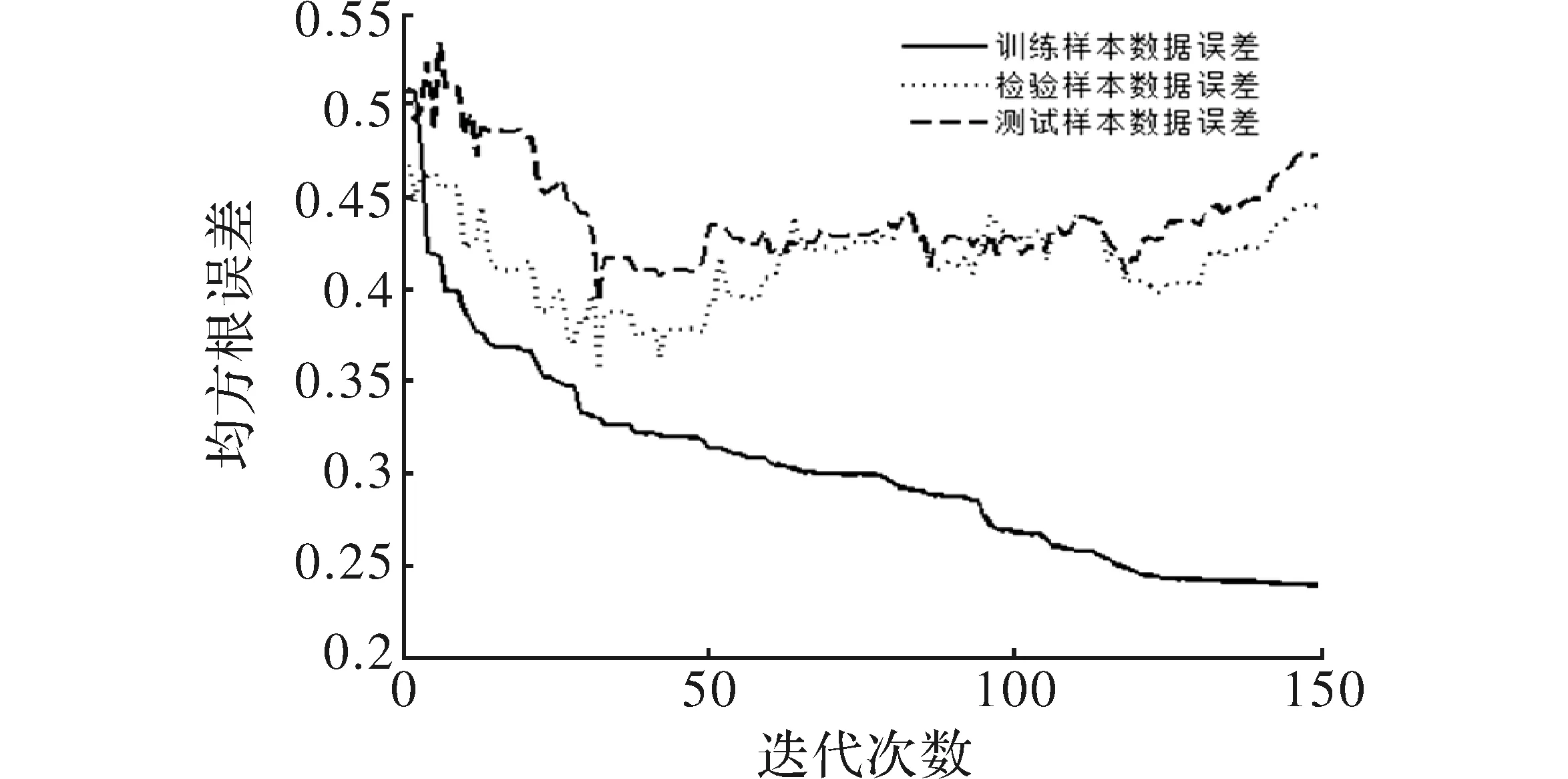
图1 训练过程

图2 迭代寻优

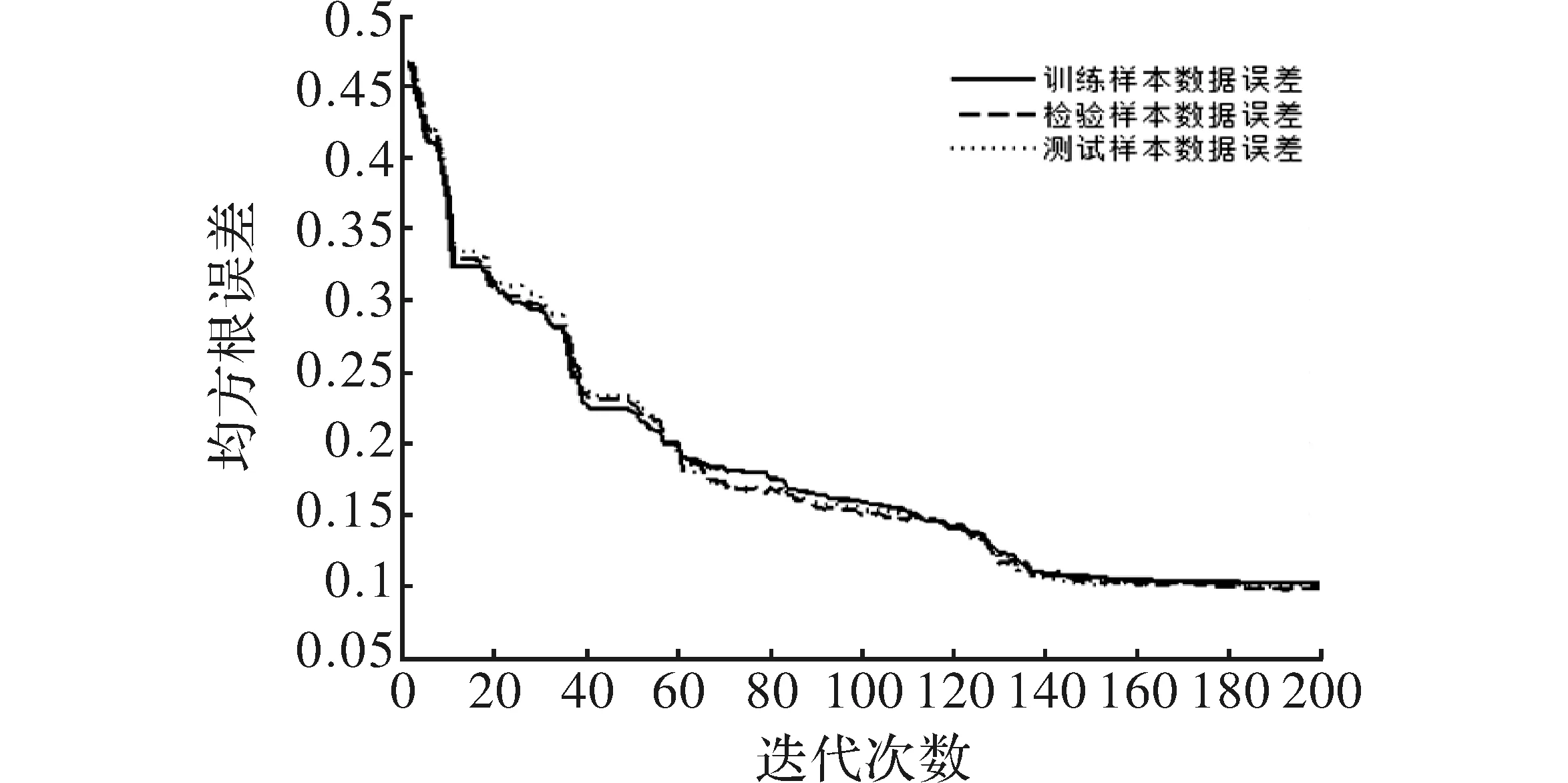
图3 基于群智能算法训练过程

图4 迭代寻优

指标训练测试检验RMSE0.06780.06780.0655BIAS-0.0400-0.03000.0200R0.96200.96800.9909R20.92650.94000.9819PA0.97550.96120.9622

3 结束语

正确合理的建立神经网络模型才会充分发挥神经网络的优势，更好的应用于实践中。群智能算法的优势在于可以求出全局最优解，避免训练过程中陷入局部最优解。在遵循建模条件情况下，基于群智能算法的神经网络能够更好的求出全局最优的权值和阈值结合检验样本监控训练，避免了过训练现象，使得训练出来的网络模型具有很好的线性逼近能力、泛化能力以及很强的可靠性。

[1] Matin T Hagan,Howard B Demuth,Mark Beale.Neural network design[M].戴葵,译.北京:机械工业出版社,2002.

[2] 楼文高.BP神经网络模型在水环境质量综合评价应用中的一些问题[J].水产学报, 2002,26(1):90-96.

[3] GarciA-Gimeno R M, Hervás-MartiNez C, Silóniz M I D.Improving artificial neural networks with a pruning methodology and genetic algorithms for their application in microbial growth prediction in food[J]. International Journal of Food Microbiology, 2002,72(1-2):19-30.

[4] 董聪.多层前向网络的全局最优化问题[J].大自然探索,1996,15(4):27-31.

[5] 寇晓丽.群智能算法及其应用研究[D]. 西安:西安电子科技大学,2009.

[6] 楼文高.BP神经网络模型在水环境质量综合评价应用中的一些问题[J].水产学报,2002,26(1):90-96.

[7] 刘志雄,梁华.粒子群算法中随机数参数的设置与实验分析[J].控制理论与应用, 2010,27(11):1489-1496.

[8] 简相超,郑君里.混沌神经网络预测算法评价准则与性能分析[J].清华大学学报:自然科学版, 2001,41(7):43-46.

[9] Betiku E,Ezekiel T A.Modeling and optimization of bioethanol production from breadfruit starch hydrolyzate vis-a-vis response surface methodology and artificial neural network[J].Renewable Energy,2015,74(C):87-94.

[10] 魏海坤,徐嗣鑫,宋文忠.神经网络的泛化理论和泛化方法[J].自动化学报,2001,27(6):806-815.

[11] Dil E A,Ghaedi M,Ghaedi A,et al. Application of artificial neural network and response surface methodology for the removal of crystal violet by zinc oxide nanorods loaded on activate carbon: kinetics and equilibrium study[J].Journal of the Taiwan Institute of Chemical Engineers,2015,33(3):429-442.

[12] Betiku E,Okunsolawo S S,Ajala S O,et al. Performance evaluation of artificial neural network coupled with generic algorithm andresponse surface methodology in modeling and optimization of biodiesel production process parameters from shea tree (vitellaria paradoxa) nut butter[J].Renewable Energy, 2015,76(C):408-417.

[13] Witek-Krowiak A,Chojnacka K, Podstawczyk D,et al.Application of response surface methodology and artificial neural network methods in modelling and optimization of biosorption process[J].Bioresource Technology,2014, 160(5):150-160.

[14] Podstawczyk D, Witek-Krowiak A, Dawiec A,et al.Biosorption of copper(II) ions by flax meal: Empirical modeling and process optimization by response surface methodology (RSM) and artificial neural network (ANN) simulation[J].Ecological Engineering,2015,83(7):364-379.

[15] Pilkington J L,Preston C,Gomes R L. Comparison of response surface methodology (RSM) and artificial neural networks (ANN) towards efficient extraction of artemisinin from Artemisia annua[J].Industrial Crops & Products,2014,58(1):15-24.

[16] Nikbakht A M,Motevali A,Minaei S. Energy and exergy investigation of microwave assisted thin-layer drying of pomegranate arils using artificial neural networks and response surface methodology[J].Journal of the Saudi Society of Agricultural Sciences,2013,13(2):81-91.

Research of Neural Network Model Based on Swarm Intelligence Algorithm

WANG Shanshan

(School of Optical-Electrical Information and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

It is not reasonable to select the appropriate weights to bring out the desired results with the global optimal solution on the misleading of local optimal solution in the process of neural network model.A swarm intelligence algorithm is used to obtain the global optimal solution and the neural network model is established by using the weight and threshold value of the sample to the lowest point. The results showed that the evaluation parameters of the network model showed good performance, the prediction accuracy and the correlation coefficient were 97.55% and 96.2% respectively among them. Examples show that the neural network based on swarm intelligence algorithm can be able to get the global optimal solution and the model has good performance under the modeling condition which can prove its great value in theory and market.

neural network; swarm intelligence algorithm; global optimal; modeling conditions

2016- 06- 01

王闪闪(1990-)，女 ，硕士研究生。研究方向：神经网络。

10.16180/j.cnki.issn1007-7820.2017.04.014

TP183

A

1007-7820(2017)04-056-04