基于声全息技术的噪声源识别与DSP实现
2017-04-21李俞霖
李俞霖,向 宇,伍 松
(广西科技大学 汽车与交通学院,广西 柳州 545006)
基于声全息技术的噪声源识别与DSP实现
李俞霖,向 宇,伍 松
(广西科技大学 汽车与交通学院,广西 柳州 545006)
针对传统噪声源识别无法充分利用声场信息以及不便于实现等问题,文中以共轭汇聚波原理及声全息法为理论基础,提出了应用二维傅里叶变换(2DFFT)计算复杂面积分的全息重建算法。根据该种算法的数据量大,运算复杂的特点,选取TI公司TMS320C6701这款超高速浮点DSP芯片,采用C和汇编语言混合编程,实现了声全息算法DSP的应用。通过实验较为准确地识别出噪声源位置,显示出此声源识别系统具有速度快、精度高、实用性强的特点。
声全息;共轭汇聚波;二维傅里叶变换;数字信号处理器
随着汽车行业的快速发展,人们对汽车的综合性能的要求不断提高,汽车噪声也成为衡量汽车舒适性的重要指标之一,降低噪声显得尤为重要,因此引起国内外学者和汽车厂商的高度关注。无论采取何种途径降低噪声,都不能回避的是对噪声源的声辐射特性进行分析,进行空间声场的可视化和噪声源的识别与定位,对噪声测量、噪声源识别和控制具有重要意义[1]。与传统噪声源识别技术相比,声全息技术 (Acoustical Holography) 具有更强的识别功能,因为此技术利用了声的强度信息的同时,还充分利用了声的相位信息[2-7]。声全息技术的基本思想是利用麦克风构成的全息阵列面得到的声场信息,借助空间声场间关系的变换算法,重建出声源表面的声学信息包括声压和法向振速等,进而利用这些声学信息完成对三维空间声场中任一点声学量的预测[8-10]。声全息技术经过多年的发展,现已形成了一套理论体系,然而现有的声全息测量分析系统比较少,且价格昂贵,影响了声全息技术的发展[11]。DSP( Digital Single Processor) 是以数字信号来处理大量信息的器件,具有强大数据处理能力和高运行速度,得到广泛应用[12-13]。采用TI公司TMS320C6701[14-15]的DSP作为硬件平台,将采集到的全息面声压数据运用全息算法在DSP上处理,进而计算出重建声场信息,使得声全息技术在噪声源的识别中具有很强的可实现性。
1 共轭汇聚原理与声全息理论
1.1 基本理论模型
这里提到的基于共轭波汇聚原理的声全息理论指的是以基尔霍夫衍射积分公式为理论基础,利用物波与参考波的干涉成像机制和共轭波在全息底片后汇聚成底片前所成虚像完全对称的实像的原理而推导得来。该声全息方法的原理图如图1所示。

图1 声全息原理示意图
图1中,H为全息面;S为重建面,二者相互平行,且间距为z0。H上的复声压分布H(X,Y)可以通过测量得到,然后取共轭得H*(X,Y)。再根据式(1)可得重建面上的声场分布,U(ξ,η)从而可识别出声源面上的噪声源。
(1)
式(1)中,重建面S上任意一点Q(ξ,η)的声场值为U(ξ,η),全息面H上任一点p(x,y)的复声压的共扼为H*(X,Y),点P(x,y)力与点Q(ξ,η)间的距离为r;k0为波数;C为全息常数,积分在全息面H上进行。
为便于进行空间频域重建公式的推导, 首先进行坐标轴的转换。将图1所示的坐标系改为图2所示的单一直角坐标系的形式。
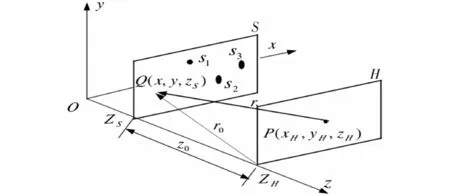
图2 单一直角坐标系的声全息原理图
在此坐标系下,式(1)变为
(2)
其中,U(x,y,zs)为重建面上任一点的复声压;U*(xH,yH,zH)为全息上任一点的复声压的共扼,为简便起见,称为全息函数。z0=zH-zS,r1为点Q(x,y,zs)与点p(xH,yH,zH)间的距离,它是坐标差(x-xH)和(y-yH)的函数。即
(3)

(4)
其中
(5)
通过式(4),Us(x,y)被表示成了一个二维卷积的形式,其核函数分别为全息函数U*H(x,y)和函数W(x,y)即
Us(x,y)=U*H(x,y)*W(x,y)
(6)
函数W(x,y)的作用为从全息数据中计算出重建面声场分布,可称之为重建函数。对式(6)两端做二维傅里叶变换,并由二维卷积定理可得
(7)
对式(7)两端同时进行二维傅里叶逆变换可得
(8)
其中,F-1表示二维傅里叶逆变换。由式(8)可看出,式(1)可通过二维傅里叶变换转化成空间频域运算,这也是利用FFT进行全息重建的理论基础。
1.2 模型离散化
在实际的试验中,不可能获取连续、无限大全息面H上的全息函数U*H(x,y),傅里叶变换和傅里叶逆变换也不可能是连续的,因此需要得出式(8)的离散形式。假设全息面是无限大的,但是全息函数的测量只是在尺度为Lx×Ly的全息面H上进行, 这样即可将对式(4)的连续积分进行离散化处理,形成式(10)的离散求和
(9)


(10)
(11)
(12)
(13)
其中,DFT[·]表示2M×2N点二维离散傅里叶变换。对式(13)作二维离散傅里叶逆变换,可得
(14)
2 系统软件设计
根据算法理论的先用软件进行仿真,采用C语言进行实现,重要的是利用Matlab上对应的C语言。在DSP开发环境CCS软件上编写C语言对全息阵列采样数据进行处理和解算。
2.1 系统流程

图3 程序流程图
程序流程图3中,麦克风阵列采集到的信号存在干扰信号,除了硬件进行滤波外,还利用数字滤波技术去除干扰信号,先将全息面上的时域信号通过傅立叶变换得到全息面频域的全息函数,经全息变换算法,最终得到重构面上的声场信息。
2.2FFT的DSP实现
对于声全息计算方法而言,需要进行大量的数值计算,进而获得整个重建面上的声场分布。将该算法进行频域化的目的就是要将全息重建变换到频域内进行,这样就可以利用FFT算法的快速性来提高全息重建的效率,增强声全息方法的适用性。
DSP的主程序用C语言进行开发,首先开发FFT算法。一维基2FFT算法编程过程:
(1)分级。在进行变换的过程中,从 点到两点共分了M级;
(2)倒位序。由于变换过程中,输出按奇、偶抽取的缘故,输出数据不是按照序列的先后顺序排列,进行输入时间序列的重排;
(3)蝶形运算单元和同址计算。蝶形运算输出结果仍放在同一储存单元;
(4)寻址和相移因子的计算。运算每一级有个蝶形单元,每一级的蝶形单元又可以分为若干组,每一组具有相同的结构和因子的分布。
二维FFT算法可以用来计算二维连续时间信号的傅里叶变换、二维离散信号的线性卷积,以及对二维离散信号进行压缩、滤波等。一般地,二维序列的点数一般比一维要大得多,采用FFT算法效益也高得多。二维FFT是在一维FFT基础上进行的,算法流程如图4所示。
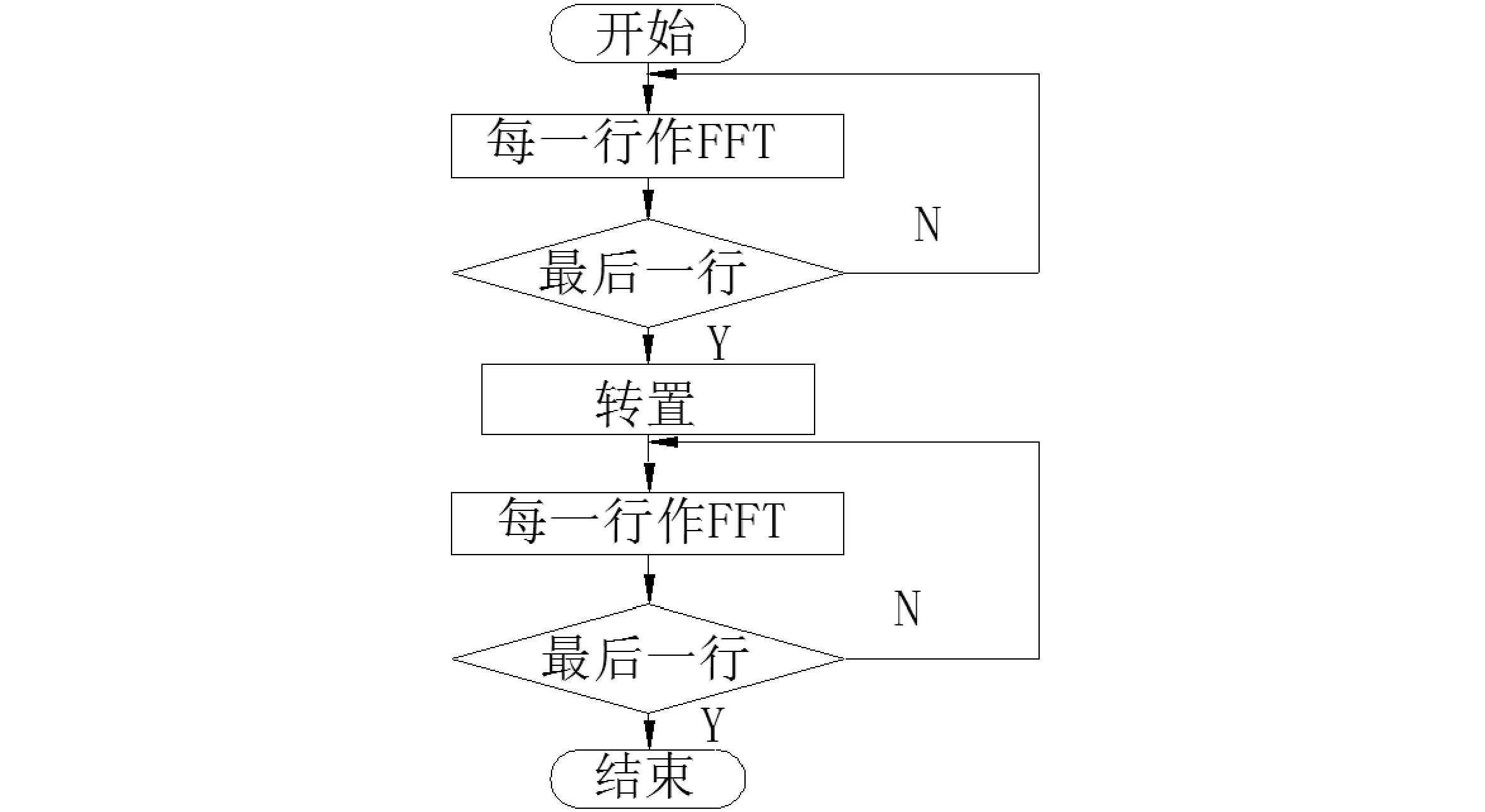
图4 二维FFT算法流程图
同样利用C语言编写二维基2FFT,函数语句为voidfft2(complexf[N1][N2]),f[N1][N2]是以复数形式存储的复数矩阵数据;类似地,也可将二维IFFT计算分解为两个一维IFFT计算,函数语句为voidifft2(complexf[N1][N2]),生成二维傅里叶变换源文件2DFFT-IFFT.c。
2.3 全息算法的实现
根据傅里叶变换信号从时域变换到频域后再进行处理的全息复声压,然后再对全息面上的复声压进行二维傅里叶变换(2DFFT)到全息面上的波数域声压得到全息函数,再用全息函数带入基尔霍夫积分公式,最后再原路逆傅里叶变换(2DIFFT)回来,得到重建面声压,如图5所示。
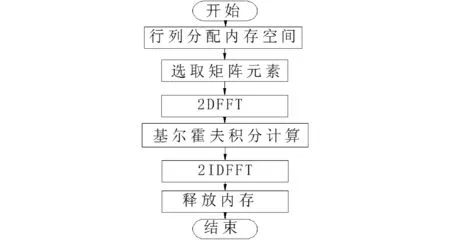
图5 全息算法
3 系统的DSP实现
根据本文算法,设计了一种基于DSP硬件平台的声传感器阵列的噪声源识别和分析系统。TMS320C6701是TI公司于的一款超高速浮点DSP芯片。主频最高可达167MHz,峰值运算能力1 000MLOPS,这为C6701的高性能提供了保障。且TI公司还开发了新的高效C编译器,可视化的Windows源程序代码调试接口,可以简化程序代码的编写与调试,32位外部存储器接口EMIF,最大外部存储器寻址空间位52MB,可直接与大容量,低成本的SDRAM芯片无缝连接,丰富的存储空间一次完成更多点的复数二维FFT。
如图6系统组成,工作流程为:声源信号由信号发生器生成,经功率放大器放大后,由音箱发生作为模拟噪声源;确定阵列与声源间距以及阵列上传声器间距、数目、采样频率和参考传声器等参数设置,传声器配套的校准器完成传声器标定;通过信号调理可传声器接收的信号进行调理,根据需要进行放大、隔离、滤波、激励及线性化等信号调理;接着对声压信号进行采集和处理,经串口传输到上位机,由上位机软件模块分析处理后得到声场数据及声学图像。
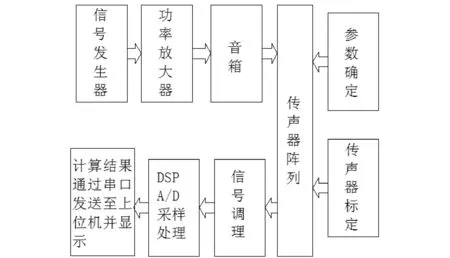
图6 系统组成框图
选择夜晚安静的环境下完成实验,尽可能减小测量背景噪声对测量的影响,如图将实验各部分连通,音箱纸盆中心为坐标系原点,全息面沿水平方向和竖直方向的间距(传声器间距离)为10cm,通过对6×6传声器阵列上传声器信号的采集,经过一系列数据处理,传输到上位机,如图7所示。

图7 声全息实验图
采集到的数据通过DSP处理,在上位机上显示的实验结果,如图8所示。经多次试验验证,在较理想的情况下测量得到的结果精确度较好,声场图像可清晰地识别出主要声源的位置和声辐射强度大小,结果与实际声源位置相当吻合,能达到预期声源识别的效果。

图8 声源面声压分布
利用全息面声压重建面 的声压分布结果如图9所示,图中清晰地显示出由纸盆向外声辐射方向各点声压的大小,并可准确的定位声源辐射场和辐射场的分布情况。

图9 重建坐标的 平面上声压幅值分布
以上单频声音箱的声源识别实验可看出,利用声全息方法可以准确识别声源的位置,也可进行声场可视化。通过利用DSP芯片配置以声全息算法实现,不仅方便调试和应用,即使数据量大和运算复杂的情况下,也能满足实时性处理的要求。
4 结束语
首先阐述了共轭汇聚原理及声全息方法的相关理论,进而提出了应用二维傅里叶变换计算复杂面积分的重建算法。重建算法包括截断、离散化、卷积等过程,此算法可大幅提髙全息重建的计算效率。采用处理速度高的TMS320C6701处理器,通过实验证明在DSP上实现文中计算方法的有效性,能较好地进行二维数据处理,满足声源识别的要求,编写精简的声全息算法来进一步提高重建声场的精度和速度,在背景噪声较小的情况下误差很小,可得到较好的重建结果,此声全息测量处理系统具有实用性。
[1]TretterSA.CommunicationsystemdesignusingDSPalgorithmswithlaboratoryexperimentsfortheTMS320C6713DSK[M].Germany:SpringerUS, 2008.
[2]SpringerScience&BusinessMedia.TMS320C6711[M].Germany:SpringerScience&BusinessMedia,2012.
[3]ZhangHaibin,JiangWeikang,WanQuan.Nearfieldacousticholographybasedonwavesuperpositionalgorithmforcyclostationarysoundfield[J].ActaPhyicaSinica,2008,57(1): 313-321.
[4] 杜向华,朱海潮,毛荣富,等.复杂声场环境下的近场声全息技术[J].海军工程大学学报,2011,23(4):80-83.
[5]RuhalarJ,SwansonDC.Planarnear-fieldacousticalholographyinamovingmedium[J].TheJounaloftheAcousticalSocietyofAmerica,2002,112(2):420-429.
[6]WilliamsEG,HoustonBH.Interiornear-fieldacousticalholographyinnight[J].AeoustScoAm, 2000,108(4):1451-1463.
[7] 刘锋,杨殿阁,郑四发,等.利用声全息方法识别噪声源问题中声源幅值修正的研究[J].声学学报,2002(3):263-266.
[8]MegavannanJ,GaikwadAA,RamachandranE,etal.AcousticholographytechniquesinautomotiveNVH[J].SAETechnicalPaper, 2009(3):1518-1525.
[9] 陈颖,吴长奇.基于麦克风阵列的声源定位算法研究及DSP实现[D].秦皇岛:燕山大学,2012.
[10] 何元安,何祚镛.用声场空间变换识别水下噪声源[J].应用声学,2000,19(2):9-13.
[11] 何元安,何祚镛,姜军.基于声强测量的近场声全息及其在水下声源声辐射分析中的应用[J].声学学报,1996(4):297-305.
[12]GratzP.Acousticalholographyforvisualizationofsoundfields[C].France:InternationalCarpathianControlConferenceICCC,2002.
[13] 陈达亮.发动机整车匹配中的振动噪声识别与控制研究[D].天津:天津大学,2008.
[14] 金程.基于DSP的实时互谱声强测量系统的研究[D].杭州:浙江大学,2007.
[15] 李青.基于LabVIEW的近场声全息噪声源识别系统[D].合肥:合肥工业大学,2010.
Noise Source Identification Based on Acoustic Holography and DSP Implementation
LI Yulin,XIANG Yu,WU Song
(School of Automobile and Transportation Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China)
Aiming at the problem that the traditional noise source identification can not make full use of the information of the sound field and inconvenient to achieve. This article put forward a new algorithm grounded on the Acoustic Holography method based on the principle of convergence of conjugated wave. The algorithm exploits 2-dimensional Fast Fourier Transformation (2D FFT) to calculate the complex surface integral thus improves the efficiency of calculation greatly. Based on this new algorithm with huge data and complex operations, the ultra high-speed floating-point DSP chip TMS320C6701 produced by TI Company is selected. Mixed by C and Assembly Language, application of acoustic holography algorithm on DSP can be realized. It is more accurate to identify the location of the noise source through the experiment and it shows the system has the features of high precision, high speed and strong practicability.
acoustic holography; convergence of conjugated wave; 2D FFT; DSP
2016- 05- 05
广西高校自然科学基金(2013YB172)
李俞霖(1990-),男,硕士研究生。研究方向:汽车NVH技术。伍松(1971-),男,高级实验师,硕士生导师。研究方向:汽车NVH及机械振动与噪声控制。
10.16180/j.cnki.issn1007-7820.2017.04.007
TN911.72
A
1007-7820(2017)04-027-05
