一类碰撞振动系统的激变和拟周期-拟周期阵发性

乐 源， 缪鹏程

(西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室, 成都 610031)

一类碰撞振动系统的激变和拟周期-拟周期阵发性

乐 源， 缪鹏程

(西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室, 成都 610031)

研究了一类三自由度碰撞振动系统的激变和阵发性。六维庞加莱(Poincaré)映射能够表示成另外一个不对称映射的二次迭代，这表明系统具有对称性。该系统普遍存在发生Hopf分岔后得到的一对共轭拟周期运动。根据动力系统的极限集理论，讨论了极限集的对称性，得到系统发生激变的条件，并引入一个距离函数判定对称性恢复和激变临界点。当共轭混沌吸引子和不稳定对称不动点的最小距离等于0时，一对共轭混沌吸引子将会与不稳定的对称不动点在其吸引域边界发生碰撞，从而导致激变。通过数值模拟，揭示了激变之后的一种新的阵发性动力学现象：拟周期-拟周期阵发性。其分岔机制是：两个共轭拟周期吸引子→两个共轭拟周期吸引子倍化→两个共轭带状混沌吸引子→一个对称混沌吸引子→一个对称拟周期引子，通过对称极限集理论来区分对称吸引子和共轭吸引子，同时采用QR法计算Lyapunov指数并用来确定吸引子的类型。激变导致的拟周期-拟周期阵发性，对于多自由度碰撞振动系统的动力学研究及优化设计具有重要意义。

碰撞振动系统；拟周期运动；激变；阵发性

具有对称性的映射动力系统普遍存在对称性恢复分岔，即：两个或多个混沌吸引子融合并形成一个对称混沌吸引子[1]。当参数穿过激变临界值时，两个吸引子同时接触吸引域的边界。这意味着两个吸引子与不稳定鞍型轨道在吸引域边界发生碰撞[2]。激变之后，系统的动力学行为展示出阵发性特征。激变诱发的阵发性这一概念用于描述动力系统在激变后出现的特殊动力学现象。文献[3]的研究结果表明，所谓的对称性破缺以及对称性增长导致的吸引子的碰撞和爆发，本质都是共轭吸引子与对称极限集之间发生碰撞的结果。然而，上述文献关于激变之后诱发的阵发性动力学现象仅仅针对混沌-混沌阵发性，目前尚未见关于拟周期运动的阵发性的研究和报道。通过研究一类具有对称性的三自由度碰撞振动系统的激变和阵发性，首次揭示了激变之后的一种新的阵发性动力学现象：拟周期-拟周期阵发性。

碰撞振动现象广泛存在于实际工程领域，例如齿轮的拍击、引擎的锤击、存在止挡冲撞的机械系统、船舶和浮体在波浪作用下的冲击振动、机器人操作器与环境接触和脱离引起的碰撞、航天器伸展系统由于关节间隙而发生冲击等。由于存在碰撞，碰撞振动系统具有强非线性和非光滑性。研究碰撞振动系统的动力学行为对于机械系统的优化设计和噪声控制具有重要意义。非线性动力学的分岔和混沌的研究是近十几年来非线性科学领域十分活跃的研究前沿[4-5]。随着非线性动力系统理论、动态测试技术和计算机技术的迅速发展，碰撞振动系统的研究进入了全新的阶段。HOLMES等[6-7]考虑单自由度碰撞振动系统，研究了周期运动的存在性和稳定性、分岔和混沌行为。对于多自由度碰撞振动系统，在分岔点处可能同时存在两种类型的分岔，这就导致了余维二分岔。各种分岔之间相互作用，对碰撞振动系统的局部动力学具有重要的影响。文献[8-11]采用中心流型—范式理论和数值模拟的方法研究了各种余维二分岔，包括Hopf-flip分岔、Hopf-Hopf分岔以及各种强共振情况下的Hopf分岔。ZHANG等[12]对振动筛系统的两类余维三分岔进行了研究。当系统某一参数穿过某个临界值时，碰撞振动系统的振子将会以零速度与刚性约束发生碰撞。这种现象在碰撞振动系统中被称为“擦边”。在擦切点处，系统的庞加莱映射是不连续的，并且会产生由这样的非光滑因素诱发的一些非典型的分岔[13-14]。近年来其他关于碰撞振动系统力学的研究参见文献[15-17]。然而目前还未见关于碰撞振动系统的对称性恢复和激变的研究报道。

文献[18-19]的研究结果表明，具有对称性的碰撞振动系统普遍存在一对共轭吸引子，并引入一个虚拟的隐式映射来捕获这对共轭吸引子。通过研究三自由度碰撞振动系统的激变和阵发性动力学现象，引入一个距离函数判定激变临界点。当共轭混沌吸引子和不稳定对称不动点的最小距离接近0时，一对共轭混沌吸引子将会与不稳定对称不动点在其吸引域边界发生碰撞，从而导致对称性恢复和激变。数值结果表明，当控制参数在一定区间变化时，共轭拟周期运动将会恢复对称性，并出现激变诱发的阵发性动力学现象。通过对称极限集的概念来区分对称吸引子和共轭吸引子，同时采用QR法计算Lyapunov指数并用来确定吸引子的类型。

1 力学模型，对称性和Lyapunov指数

图1表示一类轴向振动系统的力学模型。该系统有三个质量块M1，M2，M3，其中M2上在M3两边分别有一个刚性约束，因此是具有双侧刚性约束的三自由度碰撞振动系统。M2通过刚度为K2的线性弹簧与阻尼为C2的线性阻尼器与刚性平面相连。M1通过刚度为K1的线性弹簧，阻尼为C1的线性阻尼器与M2相连。M3通过刚度为K3的线性弹簧，阻尼为C3的线性阻尼与M2相连。质量块Mi(i=1,2,3)上作用振幅为Pi的简谐激励力。当激励力振幅很小时，系统做强迫振动，是一个线性系统。当激励力振幅增加到一定值时，M3会依次与M2上的两个刚性约束发生碰撞，系统变成强非线性系统。碰撞以一个恢复系数R来描述。假设碰撞的时间很短，与激励力的周期相比可以忽略不计。假定C1，C2，C3为比例阻尼。

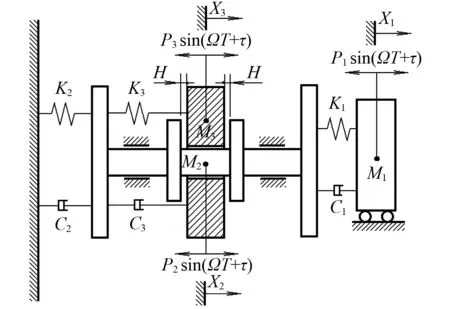
图1 具有对称刚性约束的三自由度碰撞振动系统Fig. 1 Three-degree-of-freedom vibro-impact system with symmetry

在任意两次连续碰撞之间, 无量纲化的运动微分方程为

(1)

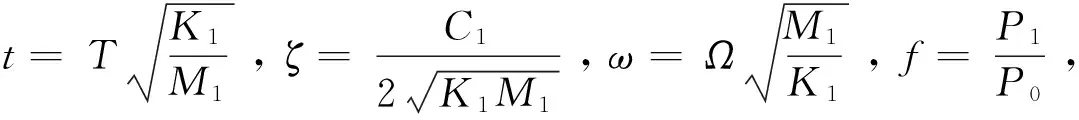
y2+=δ11y2-+δ12y3-，y3+=δ21y2-+δ22y3-

(2)

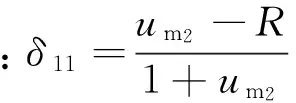
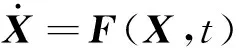
(3)

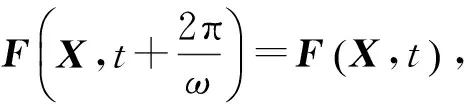
碰撞振动系统的相空间为

(4)

式中，S1为单位圆。把Poincaré截面选在与左边刚性约束碰撞后的瞬时，即

(5)

定义变换

(6)

Poincaré映射P是由四个子映射组成的：①P1映射，质量块M3与左边挡板碰撞后的瞬时运动到到与右边挡板碰撞前的瞬时所确定的映射；②P2映射，质量块M3与右边挡板碰撞的过程；③P3映射，M3质量块与右边挡板碰撞后的瞬时运动到与左边挡板碰撞前的瞬时所确定的映射；④P4映射,质量块M3与左边挡板碰撞的过程。因此，Poincaré映射可以表示为

P=P4·P3·P2·P1

(7)

Poincaré映射的Jacobi矩阵为

DP=DP4(P3·P2·P1(X0))·DP3(P2·P1(X0))×
DP2(P1(X0))·DP1(X0)

(8)

令

Q=R-1Q1

(9)

式中，Q1为与左边挡板碰撞后的瞬时运动到与右边挡板碰撞前的瞬时所确定的映射。则Poincaré映射可以写为

P=Q2

(10)

式中，Poincaré映射P是映射Q的二次迭代。令TP(x*)=Dx*P为Poincaré映射在初始点x*处的Jacobi矩阵。则

(11)

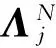
(12)

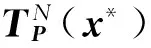
2 对称不动点与对称极限集

如果X*满足P(X*)=X*，那么X*为Poincaré映射P的不动点，对应于系统的周期运动。采用符号“(n,p)”来表示对称碰撞系统的周期运动。其中p为碰撞次数，n为激励力的周期数。因此，对称周期(n,2)(n为奇数)运动表示n个激励周期发生左右两次对称碰撞。对称碰撞是指质量块M3与左右两个挡板发生碰撞后，系统相应的坐标绝对值相等，方向相反。

定义1 (对称不动点)如果不动点X*满足

X*=Q(X*)

(13)

则X*为Poincaré映射P的一个对称(周期(n,2))不动点，对应于系统相应的对称周期(n,2)运动。

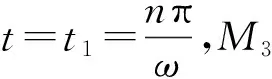
(14a)

(14b)

则存在对称不动点。

定义2 (对称极限集)如果X的ω极限集满足

ωP(X)=ωP(Q(X))

(15)

则ωP(X)为对称极限集。

引理1 如果ωP(X)是吸引子或者是周期解(不一定是吸引的)，且满足ωP(X)与ωP(Q(X))(即ωQ2k(X)与ωQ2k+1(X))的交集为非空，则ωP(X)是对称ω极限集。

引理1表明，一对共轭吸引子ωQ2k(X)与ωQ2k+1(X)发生碰撞会产生一个单一的对称吸引子。一对共轭吸引子互相碰撞意味着它们同时与不稳定鞍形轨道(即不稳定对称不动点)在吸引域的边界发生碰撞。激变导致的阵发性是指吸引子尺寸突然变大并互相融合后产生的一种特殊动力学行为。在激变临界点处，两个共轭吸引子同时接触吸引域的边界。

3 对称不动点的解析解和对称性激变

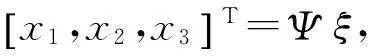
(16)

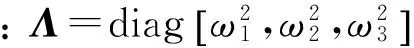
令φkj为矩阵Ψ中的元素，式(1)的解为

(17)

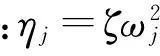
将式(17)代入式(14)得τ0，aj，bj的解为

(18a)

aj=Eajcosτ0+Fajsinτ0

(18b)

bj=Ibja1+Jbja2+Kbja3

(18c)

式中，Vc，Uc，Eaj，Faj，Ibj，Jbj，Kbj为系统参数确定的常数。将t=0和τ0，aj，bj代入式(17)得到对称不动点的解X*=(x*1,y*1,x*2,y*2,x*3,y*3)。

这里不考虑Poincaré映射的擦边分岔产生的奇异性。因此假定映射Q1，Q，P都是连续的和可逆的。相点X在P映射下的ω极限集为ωP(X)，在Q映射下的ω极限集为ωQ(X)。极限集可以是吸引和排斥

的，定义吸引子为渐近稳定的ω极限集。因为X和Q(X)是一对共轭的映射点，由X和Q(X)产生的ω极限集即ωP(X)和ωQ(X)称为一对共轭的ω极限集。

点X在映射Q下的轨道为：X，Q(X)，Q2(X)，Q3(X)，Q2k(X)，Q2k+1(X)，…由于映射P是映射Q的二次迭代，则有

Q2k(X)=Pk(X)

(19)

Q2k+1(X)=Pk(Q(X))

(20)

即映射Q的偶数次迭代即为点X在映射P下的轨道；而映射Q的奇数次迭代即为点Q(X)在映射P下的轨道。因此式(20)和式(21)隐含了ωQ2k(X)=ωP(X)和ωQ2k+1(X)=ωP(Q(X))，则有

ωQ(X)=ωP(X)∪ωP(Q(X))

(21)

又因为

Q(Pk(X))=Q2k+1(X)=Pk(Q(X))

(22)

则

(23)

即

Q(ωP(X))=ωP(Q(X))

(24)

式(15)等价于ωQ2k(X)=ωQ2k+1(X)。也就是说，如果X的ω极限等于它的共轭极限集，那么ωP(X)是对称极限集。根据式(21)，如果P和Q有相同的极限集，即ωP(X)=ωQ(X)，那么它就是一个对称的ω极限集。此外根据式(24)，如果ωP(X)通过Q映射到自身，即Q(ωP(X))=ωP(X)，则它是对称ω极限集。

此处Poincaré映射P本身不能表现出对称性，但是由式(15)可知非对称映射Q能够得到一对共存的共轭ω极限集，这表示碰撞振动系统具有对称性。

为了找到发生激变的临界点，在两个共轭吸引子与不稳定对称不动点X*(表示不稳定对称周期轨道)之间定义一个距离函数

(25)

式中：(x*1,y*1,x*2,y*2,x*3,y*3)为不稳定对称不动点的坐标；(x10,y10,x20,y20,x30,y30)为吸引子中点的坐标。Dmin=0表示ωQ2k(X)与ωQ2k+1(Q(X))有非空交集，因此是激变的临界点。

4 拟周期运动的对称性恢复和激变

4.1 拟周期吸引子的演变

考虑碰撞振动系统的系统参数：n=1，ζ=0.008 6，R=0.85，h=0.06，um3=0.6，um2=2.8，um1=1，uk3=0.8，uk2=0.2，uk1=1，uf3=0.4,uf2= 0.5，uf1=1。取系统激励力的频率ω为控制参数。当ω=3.05时，有两个共轭拟周期吸引子，在相空间中表示两个共轭的环面(见如图2(a))。为了获得一对共轭拟周期吸引子，需要给不稳定对称不动点X*(根据第3节计算)施加一个ΔX的扰动，并且通过映射Q对初始相点X=X*+ΔX进行迭代。当ω=3.05时，首先得到两个不稳定的共轭映射点，然后分别在Poincaré截面上收敛到一对共轭的拟周期吸引子(在相空间中表示为一对共轭环面)，见图2(b)。当控制参数增加到ω=2.985时，有一个单一的拟周期吸引子，见图3。由于ωQ2k(X)=ωQ2k+1(X)，所以图3所示的拟周期吸引子是对称的，映射点首先进入对称拟周期吸引子上部区域并停留一段时间，然后进入下部区域并停留一段时间，如此循环。这种在对称拟周期吸引子的两部分无限交替的过程叫做激变诱导的拟周期运动阵发性。这种拟周期运动的阵发性现象只存在于多自由度对称碰撞振动系统中，目前尚未见相关报道。图2所示的一对共轭拟周期吸引子是如何演变成如图3所示的单一的对称拟周期吸引子的？这个问题的解答需要以吸引子的对称性恢复分岔理论为基础。

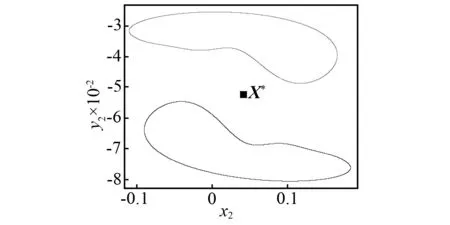
(a)一个不稳定对称不动点和一对共轭拟周期吸引子(迭代160 000次截取最后60 000个点)

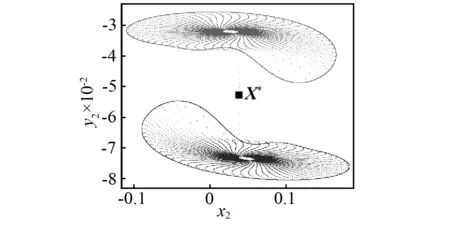
(b)从初始点X*+ΔX开始的整个收敛过程

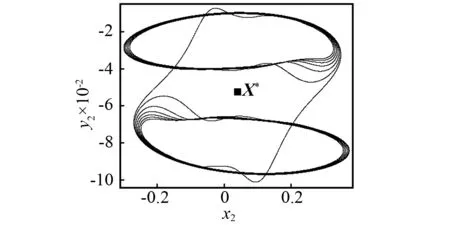
图3 一个对称拟周期吸引子：ω=2.985(迭代160 000次截取最后60 000个点)Fig.3 A symmetric quasi-periodic attractor:ω=2.985(plot the last 60 000 points after 160 000 iterations)

图2所示的一对共轭吸引子有各自的吸引域，以通过不稳定对称不动点X*的吸引域边界分开。

4.2 拟周期吸引子的激变和对称性恢复分岔

当ω增加到激变点ωc时，这对共轭吸引子就会扩大和合并，最终产生一个单一的对称吸引子。激变可以通过共轭吸引子与不稳定对称不动点的最小距离来检测，这一距离函数由式(25)定义。当ω=3.004 2时，由式(25)计算的距离D见图4。结果表明当参数ω=3.004 2时，最小距离为Dmin≈4×10-4，这一距离非常接近0。因此得出结论，在ω=3.004 2附近将发生激变。

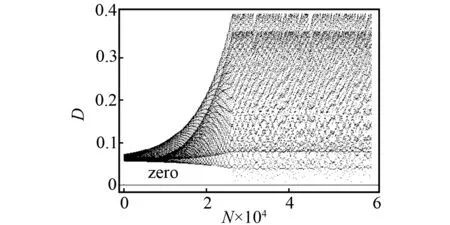
图4 拟周期吸引子与不稳定对称不动点之间的距离ω=3.004 2；Dmin≈4×10-4Fig.4 The distance between the quasi-periodic attractors and the unstable symmetric fixed point ω=3.004 2；Dmin≈4×10-4

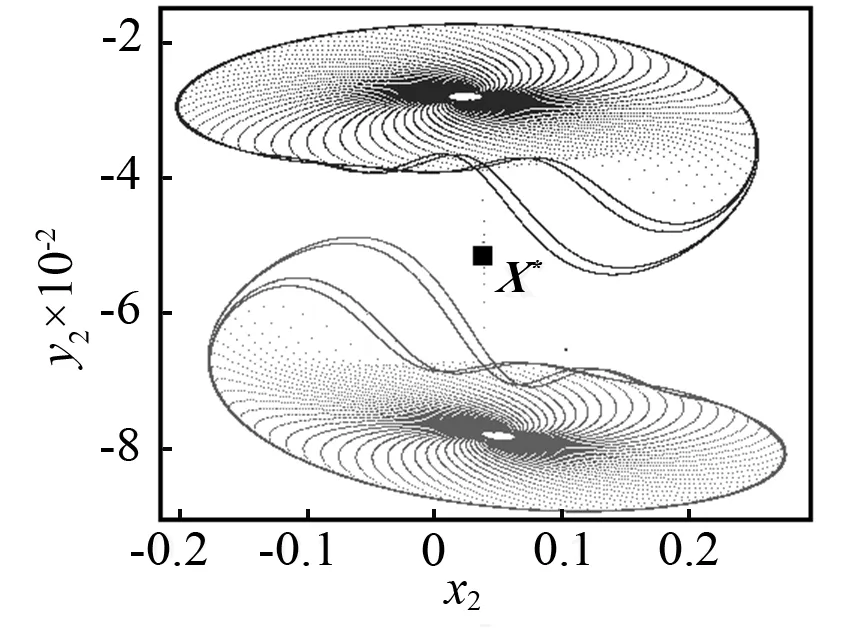
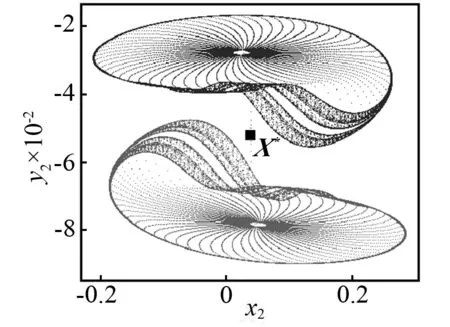
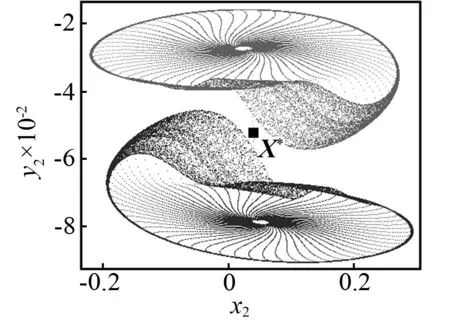
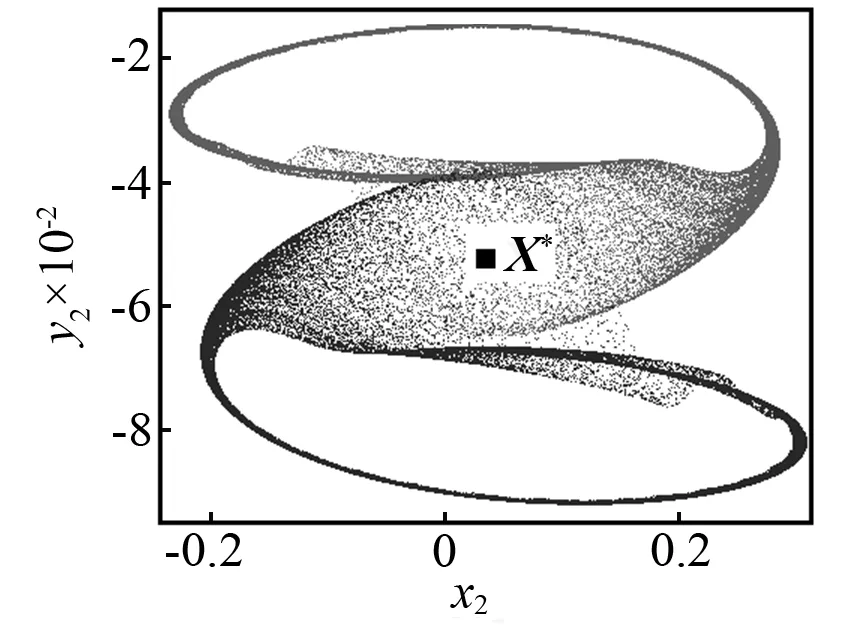
当控制参数ω减小时，Poincaré截面的投影相图如图5所示。当ω=3.018时，首先发生环面倍化，产生一个如图5(a)所示的2T环面。当ω=3.016时，通过第二次环面倍化产生一个4T环面，如图5(b)所示。当ω=3.013时，将不会有环面倍化分岔，但是将会产生如图5(c)所示的一对共轭的带状混沌吸引子。当ω=3.01时，两个共轭的带状混沌吸引子将会分别演化成一个带状混沌吸引子。如图5(d)所示，看起来非常接近不稳定不动点X*。当ω=3.005时，共轭混沌吸引子将会大幅度扩大并且会相互重叠，如图5(e)所示。看起来它们已经和不稳定对称不动点X*发生了碰撞。然而此时共轭吸引子与不稳定对称不动点的最小距离为Dmin≈8.5×10-3，这表明碰撞还没有发生。在Poincaré截面的投影相图上，这对共轭吸引子的重叠不能判断它们之间的碰撞是否已经发生，因为如图5所示的二维相图仅仅是六维相空间的投影。当ω=3.004 2时，类似的情况如图5(f)所示。然而，在这种情况下，最小距离Dmin≈4×10-4(见图4)，这一距离非常接近0。当ω=3.004 1时，两个共轭的混沌吸引子已经与不稳定对称不动点X*发生了碰撞，并且形成了一个单一的更大的混沌吸引子，如图5(g)所示。这一结果再次证实了ωc=3.004 2是吸引子碰撞的临界点。当ω减小时，例如取ω=2.985，对称混沌吸引子将会变成一个对称拟周期吸引子，如图5(h)所示。因此，拟周期运动的对称性恢复的路径是：两个共轭拟周期吸引子→两个共轭拟周期吸引子倍化→两个共轭带状混沌吸引子→一个对称混沌吸引子→一个对称拟周期吸引子。

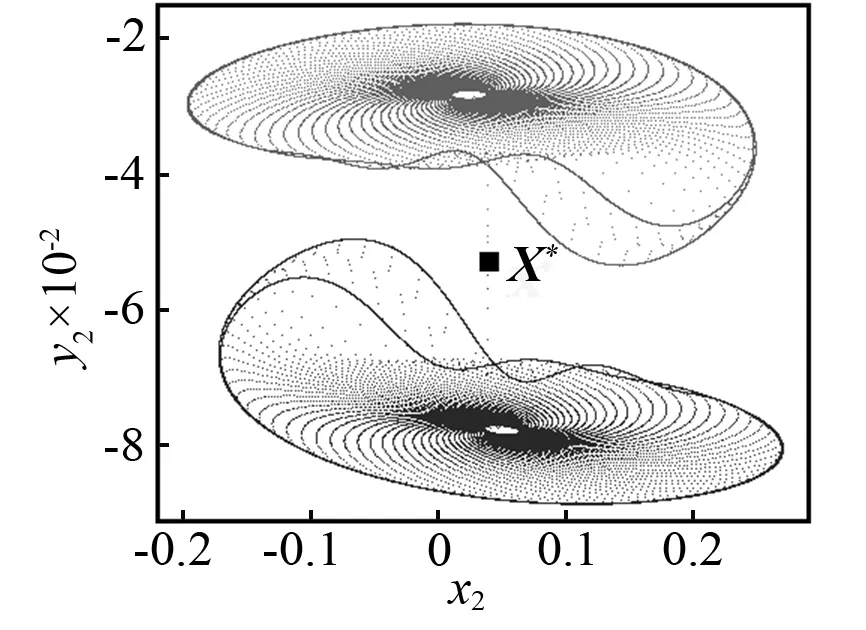
(a)ω=3.018

(b)ω=3.016

(c)ω=3.013

(d)ω=3.01

(e)ω=3.005

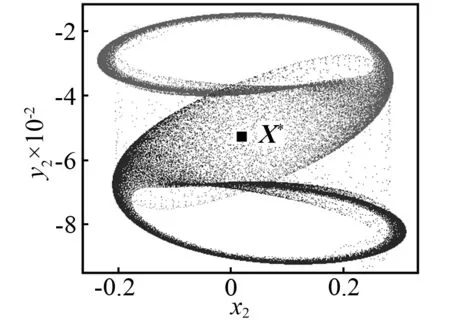
(f)ω=3.004 2

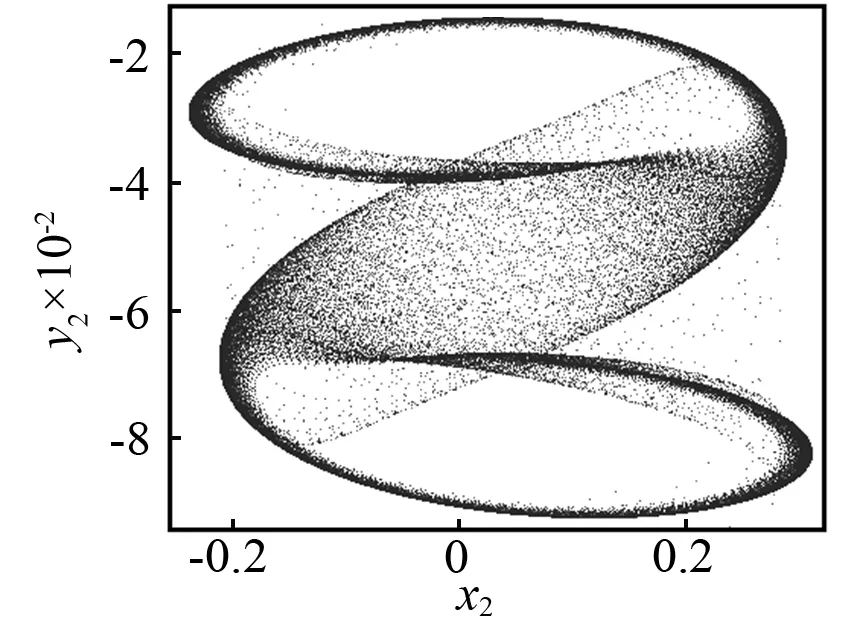
(g)ω=3.004 1

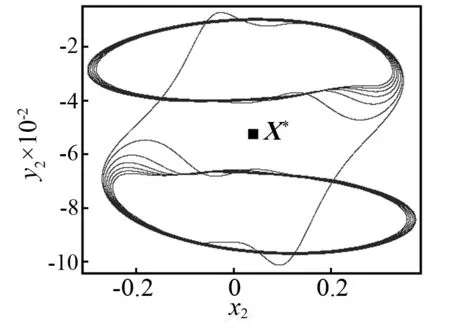
(h)ω=2.985

4.3 拟周期吸引子激变诱发的阵发性

由图6可观察到激变后诱发的阵发性。当ω=3.004 1时，两个共轭混沌吸引子同时与对称不动点接触，此时已经发生激变，并导致混沌-混沌的阵发性，如图6(a)所示。当ω=2.985时，混沌-混沌阵发性转变为拟周期-拟周期阵发性，如图6(b)所示。

以“2”节介绍的对称极限集理论为基础，通过投影相图可以区分对称吸引子和共轭吸引子。很显然，如图5(a)～图5(d)所示的两个吸引子，因为ωQ2k(X)≠ωQ2k+1(X)，所以这两个吸引子是共轭的；因为ωQ2k(X)=ωQ2k+1(X)，所以如图图5(f)和5(g)所示的两个吸引子是对称的。但是在Poincaré截面投影出现相互重叠的情况时，需要进一步的判断。例如，如图5(e)和图5(f)所示的吸引子，尽管两个吸引子在某些区域内重叠，但是它们并不是分布在整个区域，这就表示ωQ2k(X)≠ωQ2k+1(X)，因此，吸引子在这两种情况下是共轭的，但不是对称的。

Lyapunov指数是一种判断吸引子类型的有效工具，并采用第二节介绍的方法来计算。对于拟周期吸引子，至少有一个Lyapunov指数等于0。对于混沌吸引子，至少有一个Lyapunov指数大于0。可以通过如表1所示的Lyapunov指数来判断吸引子的类型。结果表明，混沌吸引子产生于吸引子碰撞激变之后，且最大的Lyapunov指数总是大于0。

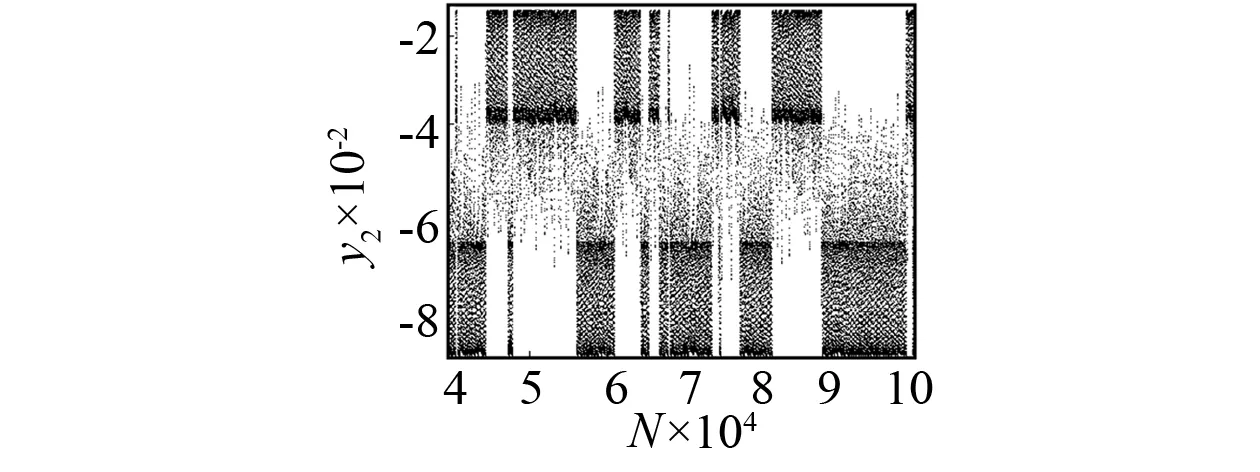
(a)ω=3.004 1

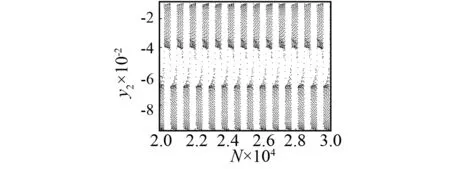
(b)ω=2.985

图号λ1λ2λ3λ4λ5λ6吸引子的类型图2(a)0.0000-0.0035-0.0487-0.0615-0.2307-0.4786拟周期图5(c)0.00220.0000-0.0470-0.0636-0.2390-0.4756混沌图5(e)0.00830.0000-0.0450-0.0666-0.2518-0.4671混沌图5(g)0.00990.0000-0.0461-0.0655-0.2570-0.4653混沌图3(a)0.0000-0.0013-0.0442-0.0442-0.2845-0.4255拟周期

5 结 论

对于对称碰撞振动系统，数值结果表明一对共轭拟周期运动能够转变成单个对称的拟周期运动，并且在发生激变之后会出现拟周期运动的阵发性现象。对称性恢复和激变在这个转换过程中具有关键作用。本文定义一个距离函数来确定激变临界点。当共轭吸引子与不稳定对称不动点在Poincaré截面上的最小距离为零时，一对共轭混沌吸引子将会同时与不稳定不动点在吸引域边界发生碰撞，这将会引起吸引子扩大和合并。拟周期运动的对称性恢复机制是：两个共轭拟周期吸引子→两个共轭拟周期吸引子倍化 → 两个共轭带状混沌吸引子 → 一个对称混沌吸引子 → 一个对称拟周期吸引子。

基于六维Poincaré映射能够表示成另外一个非对称映射的二次迭代，定义对称极限集来区分对称吸引子和共轭吸引子。QR法是一种连续正交化的手段，可以用于计算Lyapunov指数，进而判别吸引子的类型。

目前关于激变诱导的阵发性的研究，都集中在混沌-混沌阵发性，以及周期-周期阵发性[21-24]。本文揭示了碰撞振动系统中由于激变导致的拟周期-拟周期阵发性现象，这对于高维非线性动力系统吸引子的分岔研究以及碰撞振动系统的优化设计，均具有一定的理论和实践意义。

[ 1 ] CHOSSAT P, GOLUBITSKY M.Symmetry-increasing bifurcation of chaotic attractors[J]. Physica D Nonlinear Phenomena, 1988,32(3): 423-436.

[ 2 ] GREBOGI C, OTT E, YORKE J A.Chaotic attractors in crisis[J].Physical Review Letters, 1982,48(22): 1507-1510.

[ 3 ] BEN-TAL A. Symmetry restoration in a class of forced oscillators[J].Physica D Nonlinear Phenomena,2002,171(4):236-248.

[ 4 ] 王晓东, 陈予恕.一类电力系统的分岔和奇异性分析[J].振动与冲击, 2014, 33(4): 1-6. WANG Xiaodong, CHEN Yushu. Bifurcation and singularity analysis for a class of power system[J]. Journal of Vibration and Shock, 2014, 33(4): 1-6.

[ 5 ] 于海,陈予恕,曹庆杰. 多自由度裂纹转子系统非线性动力学特性分析[J].振动与冲击, 2014, 33(7): 92-98. YU Hai, CHEN Yushu, CAO Qingjie. Bifurcation analysis for a nonlinear cracked multi-degree-of-freedom rotor system[J]. Journal of Vibration and Shock, 2014, 33(7): 92-98.

[ 6 ] HOLMES P J.The dynamics of repeated impacts with asinusoidally vibrating table[J].Journal of Sound and Vibration, 1982,84(2): 173-189.

[ 7 ] SHAW S W.Forced vibrations of a beam with one-sided amplitude constraint: theory and experiment[J].Journal of Sound and Vibration, 1985,99(2):199-212.

[ 8 ] LUO G W, XIE J H.Hopf bifurcation and chaos of a two-degree-of-freedom vibro-impact system in two strong resonance cases[J].International Journal of Non-Linear Mechanics,2002,37: 19-34.

[ 9 ] XIE J H, DING W C. Hopf-Hopf bifurcation and invariant torus of a vibro-impact system[J].International Journal of Non-Linear Mechanics,2005,40(4):531-543.

[10] DING W C, XIE J H.Dynamical analysis of a two-parameter family for a vibro-impact system in resonance cases[J].Journal of Sound and Vibration, 2005,287(1/2): 101-115.

[11] YUE Y, XIE J H.Neimark-sacker-pitchfork bifurcation of the symmetric period fixed point of the poincaré map in a three-degree-of-freedom vibro-impact system[J].International Journal of Nonlinear Mechanics,2013,48(2): 51-58.

[12] ZHANG Y X, KONG G Q, YIN J N. Two codimensin-3 bifurcations and non-typical routes to chaos of a shaker system[J]. Acta Physica Sinica,2008,57(10): 6182-6187.

[13] NORDMARK A B.Non-periodic motion caused by grazing incidence in an impact oscillator[J].Journal of Sound and Vibration,1991,145(2):279-297.

[14] MEHRAN K, ZAHAWI B, GIAOURIS D. Investigation of the near-grazing behavior in hard-impact oscillators using model-based TS fuzzy approach[J]. Nonlinear Dynamics, 2012, 69(3):1293-1309.

[15] 冯进钤, 徐伟. 碰撞振动系统中周期轨擦边诱导的混沌激变[J]. 力学学报, 2013, 45:(1)30-36. FENG Jinqian, XU Wei. Grazing-induced chaostic crisis for periodic orbits in vibro-impact systems[J]. Chinese Journal of Theoretic and Applied Mechanics, 2013, 45(1): 30-36.

[16] GENDELMAN O V.Analytic treatment of a system with a vibro-impact nonlinear energy sink[J].Journal of Sound and Vibrations,2012, 331(21):4599-4608.

[17] 李飞, 丁旺才. 多约束碰撞振动系统的黏滞运动分析[J]. 振动与冲击, 2010, 29(5): 150-156.LI Fei, DING Wangcai.Analysis of the sticking motion in vibro-impact system with multiple constraints[J].Journal of Vibration and Shock, 2010, 29(5): 150-156.

[18] YUE Y, XIE J H, GAO X J.Capturing the symmetry of attractors and the transition to symmetric chaos in a vibro-impact system[J].International Journal of Bifurcation and Chaos,2012,22(5): 56-64.

[19] YUE Y, XIE J H, YUE Y.Lyapunov exponents and coexistense of attractors in vibro-impact systems with symmetric two-sided constraints[J].Physics Letters A, 2009, 373(23):2041-2046.

[20] ECKMANN J P, RUELLE D.Ergodic theory of chaos and strange attractors[J].Reviews of Modern Physics, 1985, 57(4):273-312.

[21] MANFFRA E F, CALDAS I L,VIANA R L, et al. Type-Ⅰintermittency and crisis-induced intermittency in a semiconductor laser under injection current modulation[J]. Nonlinear Dynamics, 2002,27(2):185-195.

[22] WERNER J P,STEMLER T, BENNER H. Crisis and stochastic resonance in Shinrili’scircuit[J]. Physica D Nonlinear Phenomena, 2008, 237(6):859-865.

[23] CHIAN A C L, REMPEL E L, ROGERS C. Complex economic dynamics: chaotic saddle, crisis and intermittency[J]. Chaos Solitons & Fractals, 2006, 29(5):1194-1218.

[24] TCHISTIAKOV V. Detecting symmetry breaking bifurcations in the system describing the dynamics of coupled arrays of josephson junctions[J].Physical D Nonlinear Phenomena, 1996, 91(1/2):67-85.

Crisis and quasiperiod-quasiperiod intermittency in a vibro-impact system

YUE Yuan, MIAO Pengcheng

(Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031,China)

Crisis and quasiperiod-quasiperiod intermittency in a 3-DOF vibro-impact system with symmetry were studied. The system’s 6-dimensional Poincaré map was expressed as the second iteration of another unsymmetric map, it implied that the system has a symmetry.Two conjugate quasi-periodic motions, coming from two conjugate periodic motions after Hopf bifurcation coexisted widely in such a dynamic system. According to the limit set theory of dynamic systems and the symmetry of the limit set, a distance function was introduced to detect the crisis of symmetry increasing. It was shown that when the minimum distance between a pair of conjugate chaotic attractors and an unstable symmetric fixed point is close to zero, a pair of conjugate chaotic attractors do not collide with the unstable symmetric fixed point on the attracting field boundary, to lead to a crisis. Numerical simulations revealed that a new intermittency behavior named the quasiperiod-quasiperiod intermittency occurs; the mechanism of symmetry restoring of quasi-periodic motion is two conjugate tori (quasi-periodic) → doubling of two conjugate tori → two conjugate band chaos attractors → a pair of symmetric chaos attractors → one symmetric torus (quasi-periodic); the symmetric limit set is introduced to distinguish symmetric attractors from conjugate ones; Lyapunov exponent spectrum computed with QR method is used to determine the type of attractors; the quasiperiod-quasiperiod intermittency is of importance for the optimization design of vibro-impact systems.

vibro-impact system; quasi-periodic motion; crisis; intermittency

国家自然科学基金资助(11672249；11272268；11172246)

2015-11-25 修改稿收到日期：2016-03-07

乐源 男，博士，教授，1974年2月生

O322

A

10.13465/j.cnki.jvs.2017.07.001