具有约束层阻尼旋转复合材料轴的动态特性研究

时玉艳， 任勇生， 张玉环

(山东科技大学 机械电子工程学院，山东 青岛 266590)

具有约束层阻尼旋转复合材料轴的动态特性研究

时玉艳， 任勇生， 张玉环

(山东科技大学 机械电子工程学院，山东 青岛 266590)

复合材料驱动轴在高速旋转下的振动抑制，是先进直升机和汽车传动系统结构设计需要考虑的重要问题。约束层阻尼技术是工程领域内普遍采用的实用有效的阻尼减振设计方法；然而通过采用约束层阻尼处置方式增加复合材料传动轴的阻尼能力的研究报道，目前国内外很少见到。从应力-应变关系、应变-位移关系出发，推导出复合材料Timoshenko轴、约束层与黏弹性层的动能及势能的数学表达式，采用 Hamilton原理建立具有约束层阻尼的旋转复合材料轴的运动学方程。采用广义Galerkin法对动力学方程进行了离散化，建立了广义坐标表示的自由振动方程组，通过特征值求解得到系统的固有频率和阻尼比；基于比例阻尼假设和四阶Runge-Kutta数值积分方法求解上述方程，得到系统的自由振动响应曲线。通过数值分析揭示了约束层材料、黏弹性层材料、铺层方式、长径比和转速对具有约束层阻尼的旋转复合材料轴的固有振动特性以及自由振动响应特性的影响。

被动约束层阻尼；复合材料轴；转子系统；阻尼自由振动

驱动轴是用于直升机和汽车动力传输系统中的一类重要的结构部件。与金属材料轴相比，复合材料由于具有重量轻、比强度和比刚度高等优点，因此，正在逐步取代金属材料，在现代航空和汽车驱动轴结构设计中获得越来越广泛的应用[1-5]。高性能飞机和汽车的研制对复合材料驱动轴在高速和超高速跨临界旋转状态下的振稳定性和工作可靠性，提出了更高的要求，因此，采用实用有效的方法对旋转复合材料驱动轴实现振动抑制，就显得十分重要。

被动约束层阻尼是通过利用粘贴于受控结构与约束层之间的高阻尼黏弹性材料耗散结构的振动能量，从而达到减振的目的。约束层阻尼的概念自20世纪50年代提出以来，已经发展成为一个成熟的结构振动控制技术。采用被动约束层阻尼处置能够在很宽的温度和频率范围内获得较高的阻尼比，具有设计简单、减振性能可靠等优点，是工程界普遍认可的结构振动控制措施之一[6]。

近年来，约束层阻尼结构的研究成果主要集中在含约束层阻尼的非旋转各向同性材料梁、板和壳类结构的阻尼特性研究方面[7-13]，而对于旋转轴，尤其是针对旋转各向异性复合材料轴的研究报道较少。NAPOLITANO等[14]等对具有约束层阻尼和拉-扭耦合的复合材料旋转轴进行了阻尼性能研究。他们通过有限元仿真和实验分析，发现扭转阻尼可以通过设计来实现。VENKATACHALAM等[15]对具有不同约束层阻尼的轴-盘系统进行了数值分析和试验研究，采用基于板壳理论的半解析有限元法，分析了该系统的固有频率和损耗因子。GHONEIM等[16]基于动力平衡方法建立具有部分约束层的Timoshenko复合材料轴的运动方程，并结合有限元法和假设振型法，对轴的阻尼能力进行研究。

REN等[17]从复合材料单层的三维应力应变关系和Timoshenko梁理论出发，在导出复合材料夹层轴的动能和势能表达式的基础上，采用Hamilton原理建立了具有约束层阻尼的旋转复合材料轴的拉-弯-扭耦合运动方程，采用广义Galerkin法对运动方程进行数值求解，通过对约束层阻尼复合材料轴的自由振动方程进行特征值分析，得到约束层阻尼复合材料轴的前三阶固有频率和阻尼比，研究了约束层厚度、阻尼层厚度的影响。

本文在REN等工作的基础上，进一步考察约束层材料、纤维铺层方式、长径比和黏弹性材料剪切模量，对旋转复合材料轴的固有频率及阻尼特性的影响。基于比例阻尼假定,建立了具有约束层阻尼的复合材料轴自由振动时间响应分析模型，采用四阶龙格-库塔法进行数值积分，研究了不同参数对轴的自由振动响应特性的影响。

1 理论建模

如图1所示，长度为L的复合材料轴，是由复合材料轴、黏弹性层和约束层组成。其中r为复合材料轴的任意层的半径，rs是轴的内径。hs，hv和hc分别为轴的厚度、黏弹性层的厚度和约束层的厚度。

为了建立具有约束层阻尼的旋转复合材料轴的动力学方程，利用Hamilton原理

(1)

式中,δT=δTs+δTc+δTv，δU=δUs+δUc+δUv，下标“s”、“c”和“v”分别为轴、约束层和黏弹性层。

复合材料轴、约束层和黏弹性层的动能分别表示为

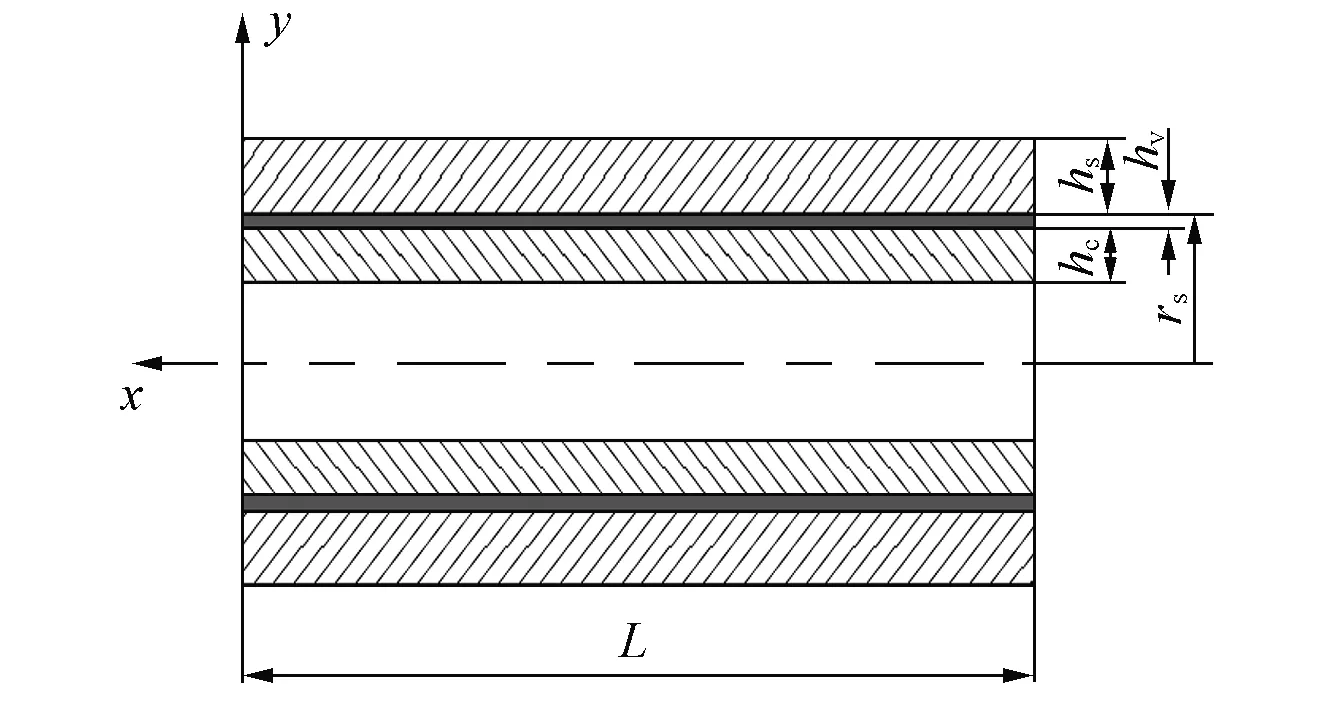
(a)

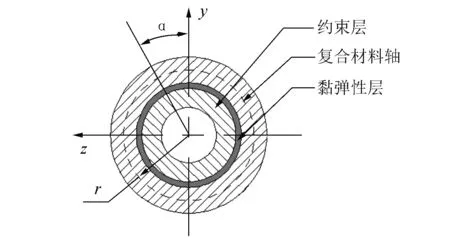
(b)图1 具有约束层阻尼的复合材料轴Fig. 1 Composite shaft with a constrained layer damping

(2)

(3)

(4)

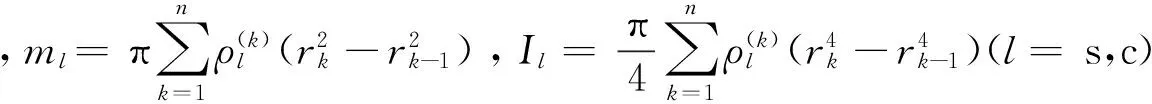
复合材料轴、约束层及黏弹性层的势能分别为

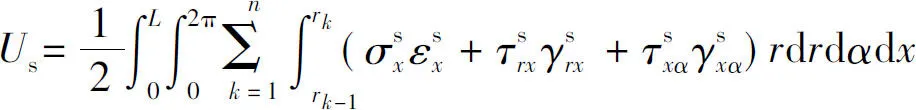
(5)

(6)

(7)

在柱坐标系 (x,r,α)下，复合材料轴和约束层的任意一层的本构关系为

(8)

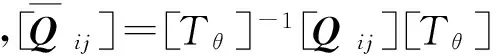
根据梁理论，σr,σα和ταx可以不予考虑。但在高速旋转状态下，应力σr,σα一般不为0，应当予以保留，但σr和σα的具体形式暂不确定，可以假设它们为轴对称。由式(8)的第一、第二和第六个方程可知，εr,εα和γrα能够用εx,γαx,γxr,σr和σα表示。

引入Timoshenko剪切修正系数κ[18]，得到表达式

(9)

根据Timoshenko梁理论，复合材料轴和约束层内任意一点的应变表示为

(10)

黏弹性层的本构关系为

(11)

式中,Gv为黏弹性层的复数剪切模量。

(12)

将式(9)和式(10)代入式(5)和式(6)，将式(11)和式(12)代入式(7)，分别进行变分并代入式(1)，得位移表示的弯曲-横向剪切耦合运动方程如下

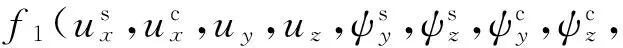
(13)

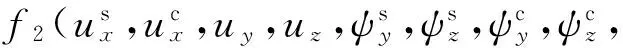
(14)

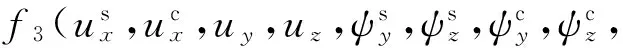
(15)

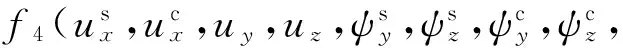
(16)

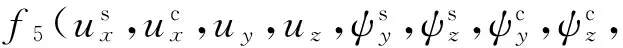
(17)

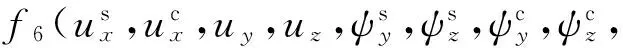
(18)

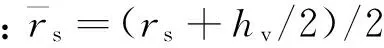
设轴的两端具有简支边界条件

uy(0)=uz(0)=0,uy(L)=uz(L)=0

(19)

(20)

为了得到复合材料轴的近似解，设位移和转角的表达式为

(21)

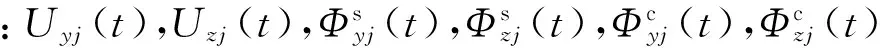
(22)

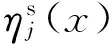
(23)

式中，[M]、[G]和[K]分别为质量矩阵、陀螺矩阵和刚度矩阵。

振动方程式(23)能够进一步化为广义特征值问题

Ay=λy

(24)

其中，

(25)

对振动系统式(24)进行特征值问题求解，可以得到系统的各阶固有频率和阻尼比。

为了简化对自由振动响应问题的分析过程，具有约束层阻尼的旋转复合材料轴的结构阻尼对振动响应的影响，基于Raleigh假设，通过引入如下比例阻尼矩阵进行分析

[C]=a0[M]+a1[K]

(26)

式中:[M]和[K]分别为轴的模态质量矩阵和模态刚度矩阵；a0,a1为比例系数，由式(27)确定

(27)

式中：ω1和ω2为轴的前两阶固有频率；η1和η2为相应前两阶阻尼比，这些固有频率和阻尼比参数可以通过自由振动分析得到。

将比例阻尼矩阵式(26)与运动方程式(23)中的陀螺矩阵[G]相叠加，得到系统的阻尼矩阵，对此阻尼自由运动方程进行数值积分，可获得系统的自由振动时间响应曲线。

2 数值结果与分析

以具有约束层阻尼的旋转复合材料轴为研究对象，轴的材料为石墨环氧树脂(简称石墨/环氧)，材料常数为：E11=139 GPa，E22=11 GPa，G12=G13=6.05 GPa，G23=3.78 GPa,v12=0.313,ρs=1 578 kg/m3；轴的基本几何尺寸为：轴的截面平均半径50 mm，总厚度为4 mm，约束层总厚度为2 mm。黏弹性层厚度为2 mm。对振动方程式(24)采用特征值技术进行固有振动特性分析，可得到固有频率和阻尼比。

2.1 固有频率与阻尼比

2.1.1 约束层材料的影响

轴长L=1 m，共10层等厚，铺层方式[θ/-θ]5。约束层分别采用高模量碳纤维环氧树脂(简称高模碳/环氧)、石墨/环氧、钢和铝材料。其中，高模碳/环氧和石墨/环氧复合材料的铺层方式[β/-β]，铺层角分别取β=0°、β=45°、β=90°，高模碳/环氧的材料常数为：E11=449 GPa，E22=9.3 GPa，G12=G13=3.24 GPa，G23=3.31 GPa，ν12=0.31，ν23=0.39，ρ=1 732 kg/m3；钢材料常数为：E=207 GPa，G=79.6 GPa，ν=0.3,ρ=7 680 kg/m3；铝材料常数为：E=69 GPa，G=26 GPa，ν=0.33,ρ=2 800 kg/m3；黏弹性材料Gv=69(1+i)MPa，ρv=1 575 kg/m3。

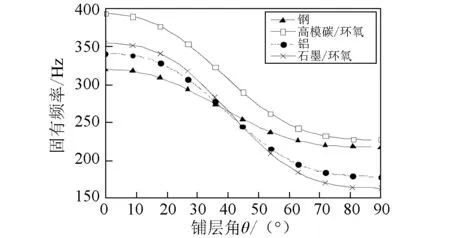
图2～图4表示转速Ω=0 ，具有不同约束层材料，约束层的铺层角分别取0°、45°和90°时，固有频率和阻尼比随轴的铺层角的变化曲线。结果表明，随着约束层复合材料铺层角的增加，固有频率和阻尼比表现出明显下降的趋势。当β=0°时，采用复合材料约束层轴相对于采用金属材料约束层轴的固有频率和阻尼比而言，总体上有较大的增加；当β=90°时，具有复合材料约束层轴的固有频率和阻尼却低于具有金属材料约束层轴的固有频率和阻尼。原因是复合材料约束层弹性主方向1上的弹性模量与金属材料弹性模量相比，数值相当或者较大，而复合材料约束层弹性主方向2上的弹性模量明显小于金属材料弹性模量。由此可见，为了能够最大限度地提高轴的阻尼能力，同时不会以牺牲轴的固有频率为代价，宜采用复合材料特别是高模量复合材料作为约束层。此外，从图2～图4中还可知，复合材料轴的铺层角θ对于固有频率和阻尼比也会产生明显的影响。

图5(a)～图5(b)表示具有不同约束层材料的轴固有频率和阻尼比随转速的变化曲线。结果表明，由于陀螺效应的存在，随着转速的增加，固有频率和阻尼比曲线分叉为上下两支，上支随着转速的增加而增加，下支随着转速的增加而减小。由图5(a)可知，对于给定的转速Ω，固有频率从大到小排列相对应的约束层材料依次是高模碳/环氧、石墨/环氧、钢和铝；由图5(b)可知，阻尼比从大到小排列相对应的约束层材料依次是高模碳/环氧、石墨/环氧、钢和铝。这与图2(a)～图2(b)是一致的。

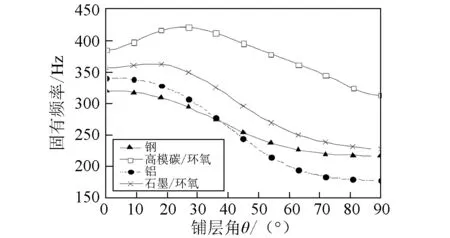
(a)固有频率

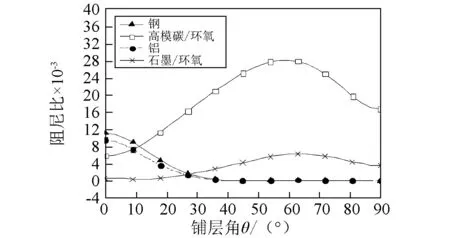
(b)阻尼比图2 不同约束层材料复合材料轴固有频率和阻尼比随铺层角的变化曲线( β=0°) Fig. 2 The natural frequency and damping ratio versus fiber angle θ for various material of constraining layer( β=0°)

(a)固有频率

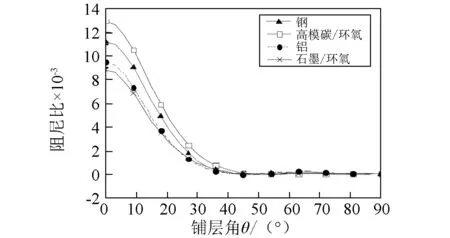
(b)阻尼比图3 不同约束层材料复合材料轴固有频率和阻尼比随铺层角的变化曲线( β=45°) Fig. 3 The natural frequency and damping ratio versus fiber angle θ for various material of constraining layer( β=45°)

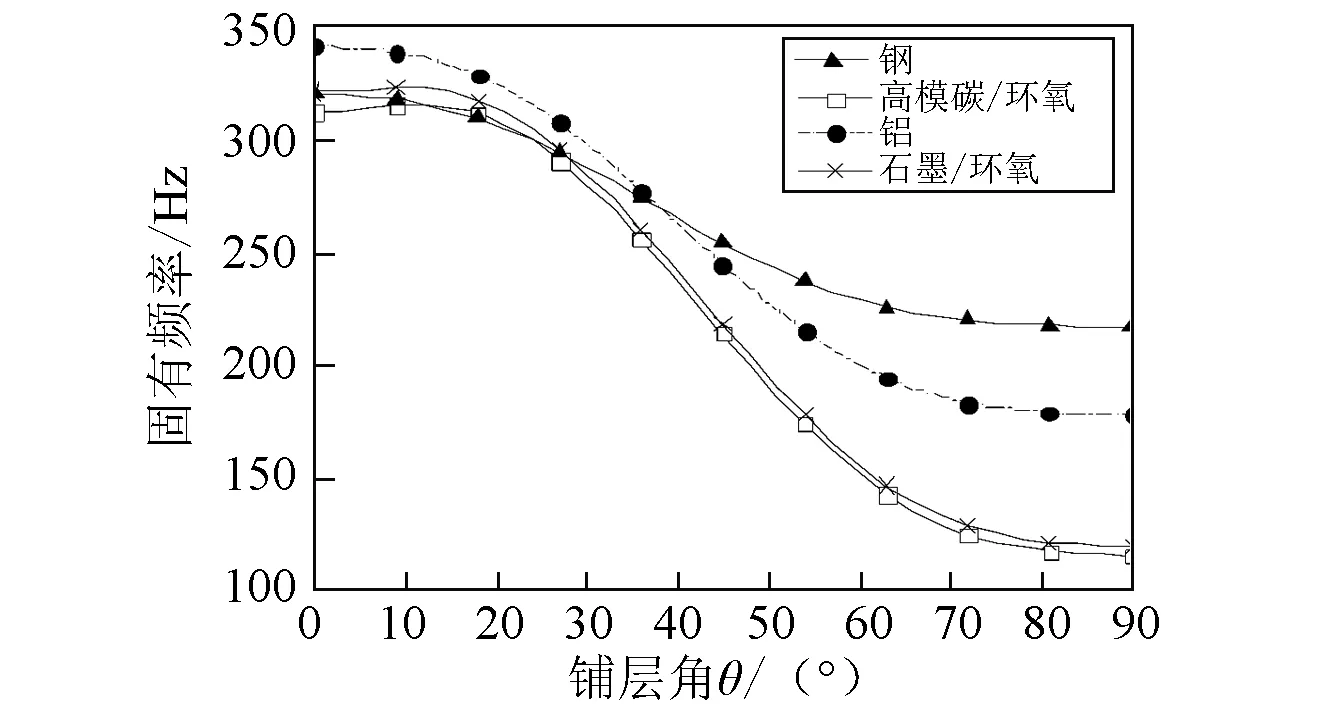
(a)固有频率

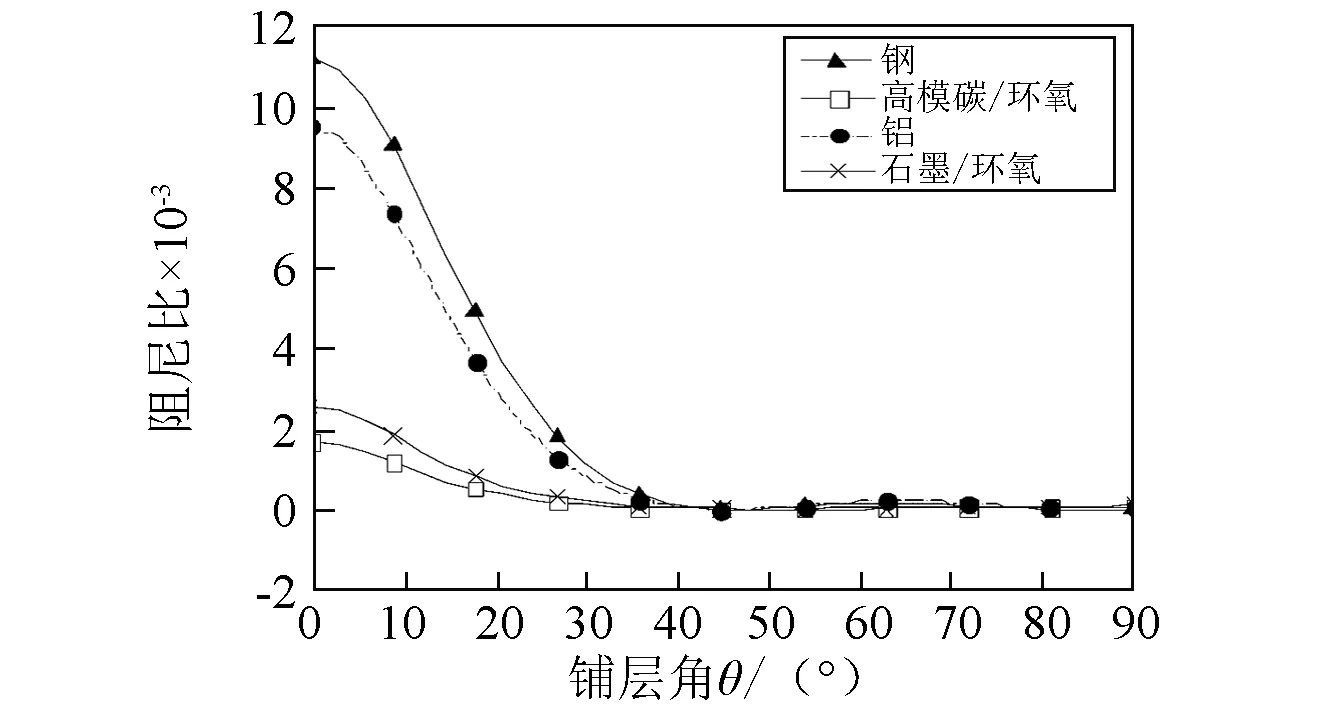
(b)阻尼比图4 不同约束层材料复合材料轴固有频率和阻尼比随铺层角变化曲线( β=90°) Fig. 4 The natural frequency and damping ratio versus fiber angle θ for various material of constraining layer( β=90°)

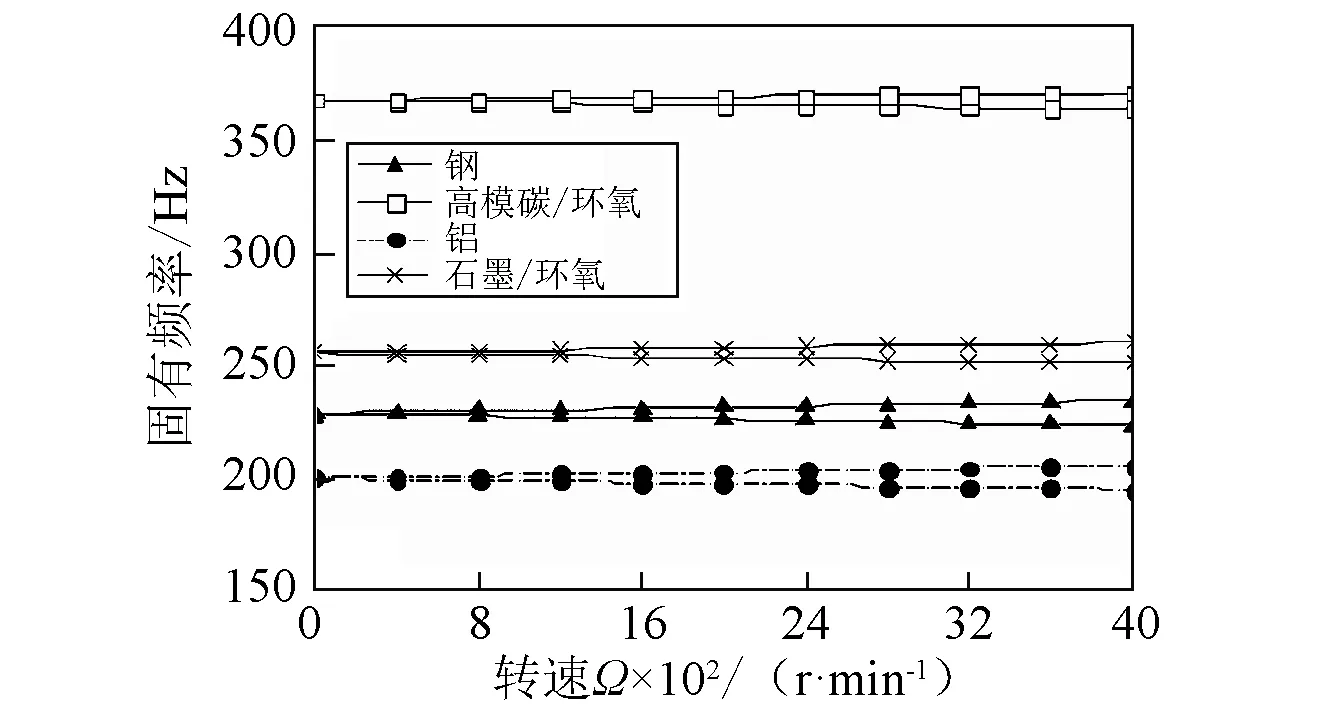
(a)固有频率

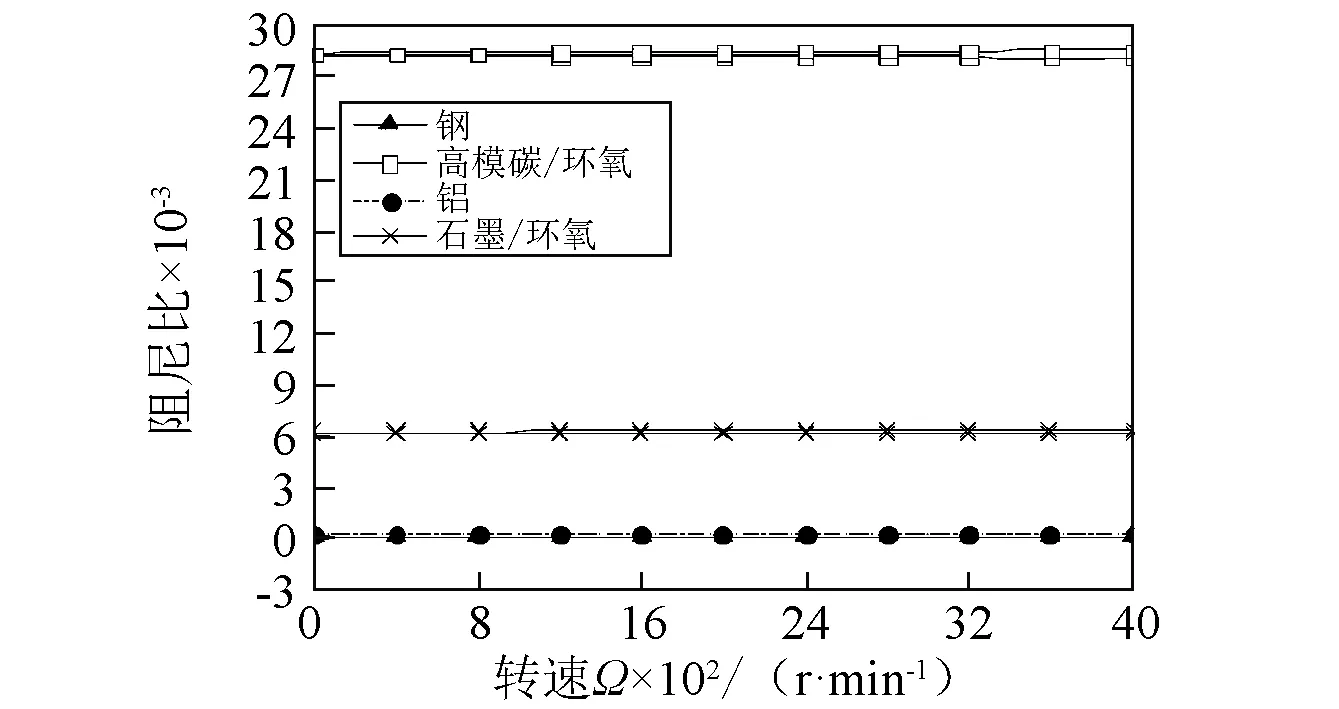
(b)阻尼比图5 不同约束层材料复合材料轴固有频率和阻尼比随转速变化曲线( β=0°,θ=60°)Fig. 5 The natural frequency and damping ratio versus rotating speed Ω for various material of constraining layer( β=0°,θ=60°)

2.1.2 轴的铺层方式的影响

轴长L=1 m，共10层等厚，分别采用[θ/-θ]5和[θ]10两种铺层方式；约束层的材料为高模碳/环氧, 共2层等厚，铺层方式[β/-β]，β=0°；黏弹性材料剪切模量为Gv=69(1+i)MPa，ρv=1 575 kg/m3。

图6(a)～图6(b)表示转速Ω=0时，在具有不同铺层方式的情况下，固有频率和阻尼比随铺层角的变化曲线。结果表明，与铺层方式[θ/-θ]5对应的固有频率，高于与铺层方式[θ]10对应的固有频率，对于阻尼比而言，其值的大小与铺层方式的关系与上述结论相反。当铺层角大于65°时，两种铺层方式下的固有频率和阻尼比曲线基本重合。

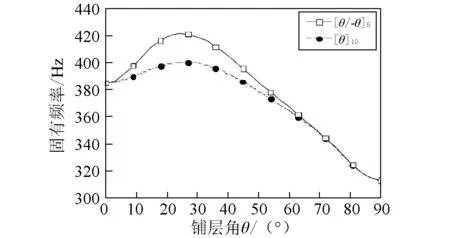
(a)固有频率

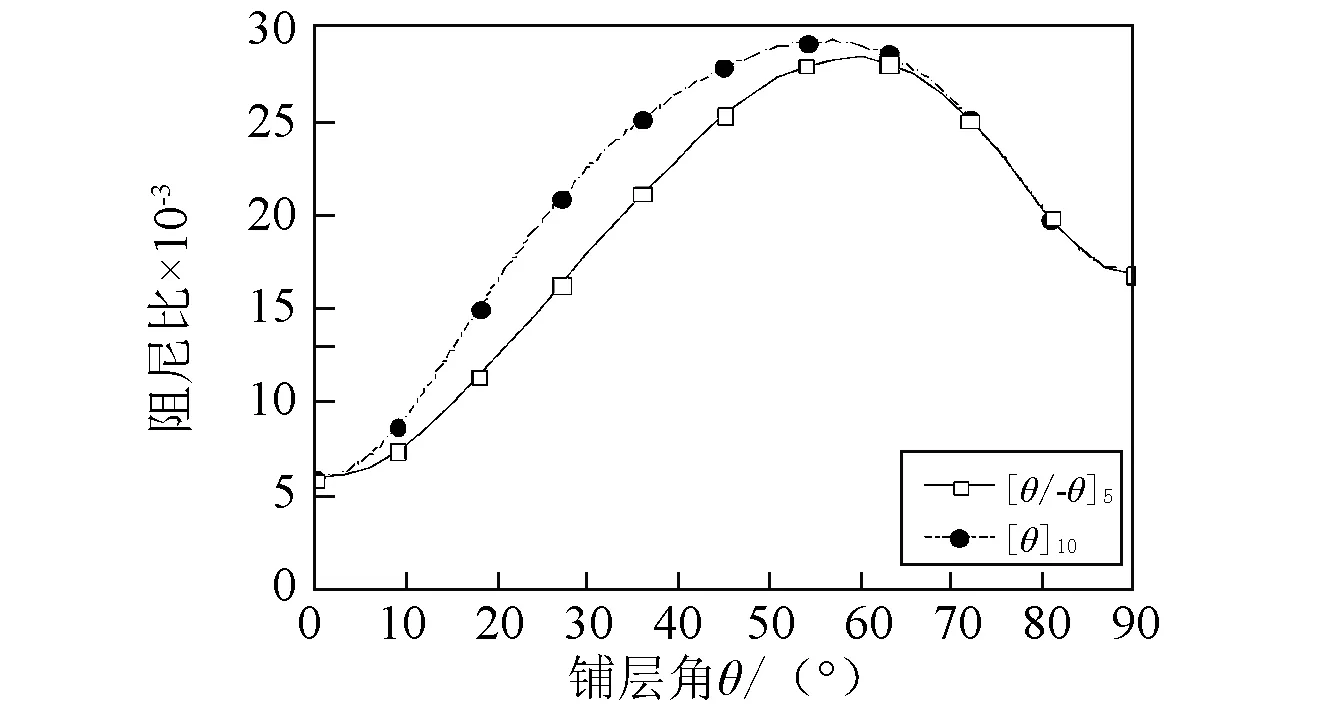
(b)阻尼比图6 不同铺层方式下复合材料轴固有频率和阻尼比随铺层角变化曲线( β=0°)Fig. 6 The natural frequency and damping ratio versus fiber angle θ for various stacking sequences( β=0°)

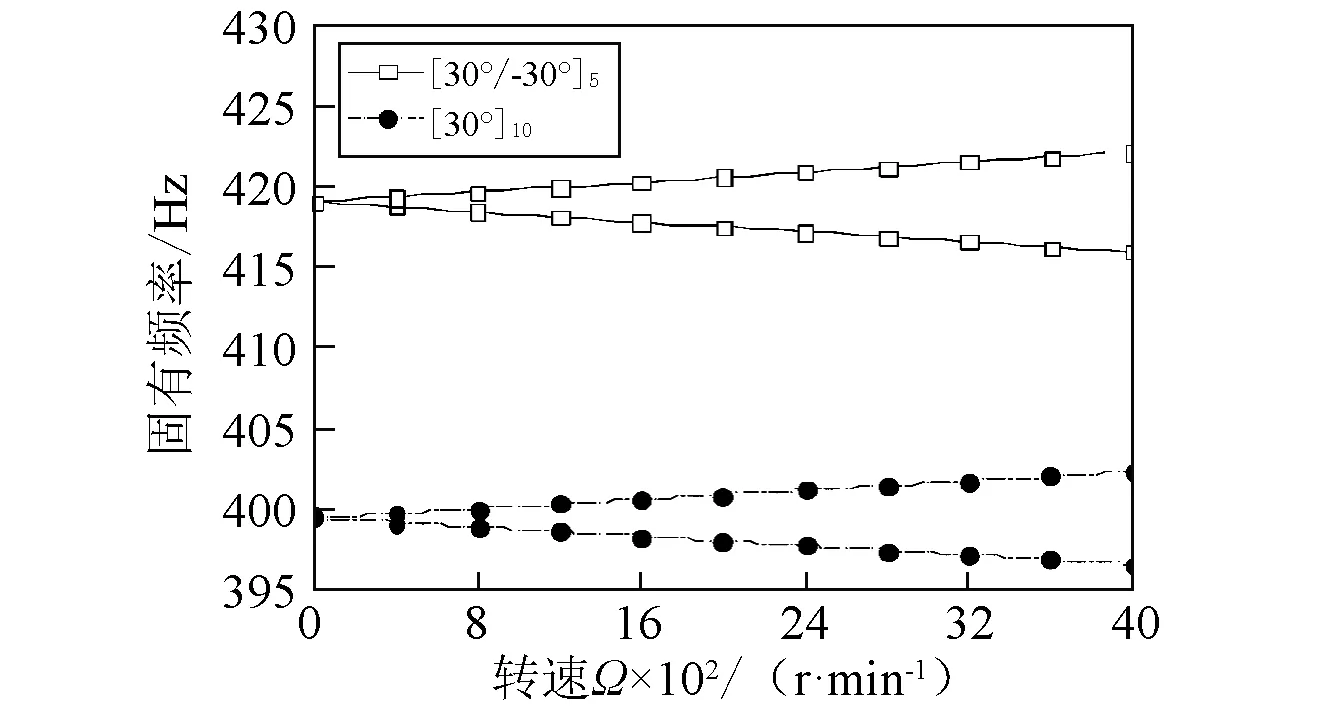
图7(a)～图7(b)表示铺层角θ=30°时，对应于不同铺层方式的固有频率和阻尼比随转速的变化曲线。结果表明，固有频率和阻尼比大小与铺层方式的对应关系，分别与图6(a)和图6(b)是一致的。

2.1.3 长径比的影响

轴长分别采用L=0.5 m、L=1 m、L=1.5 m，L=2.5 m(即轴的长度与轴的截面半径之比分别为10、20、30、50)，共10层等厚，铺层方式[θ/-θ]5；约束层的材料为高模碳/环氧, 共2层等厚，铺层方式[β/-β]，β=0°；黏弹性材料剪切模量为Gv=69(1+i)MPa，ρv=1 575 kg/m3。

(a)固有频率

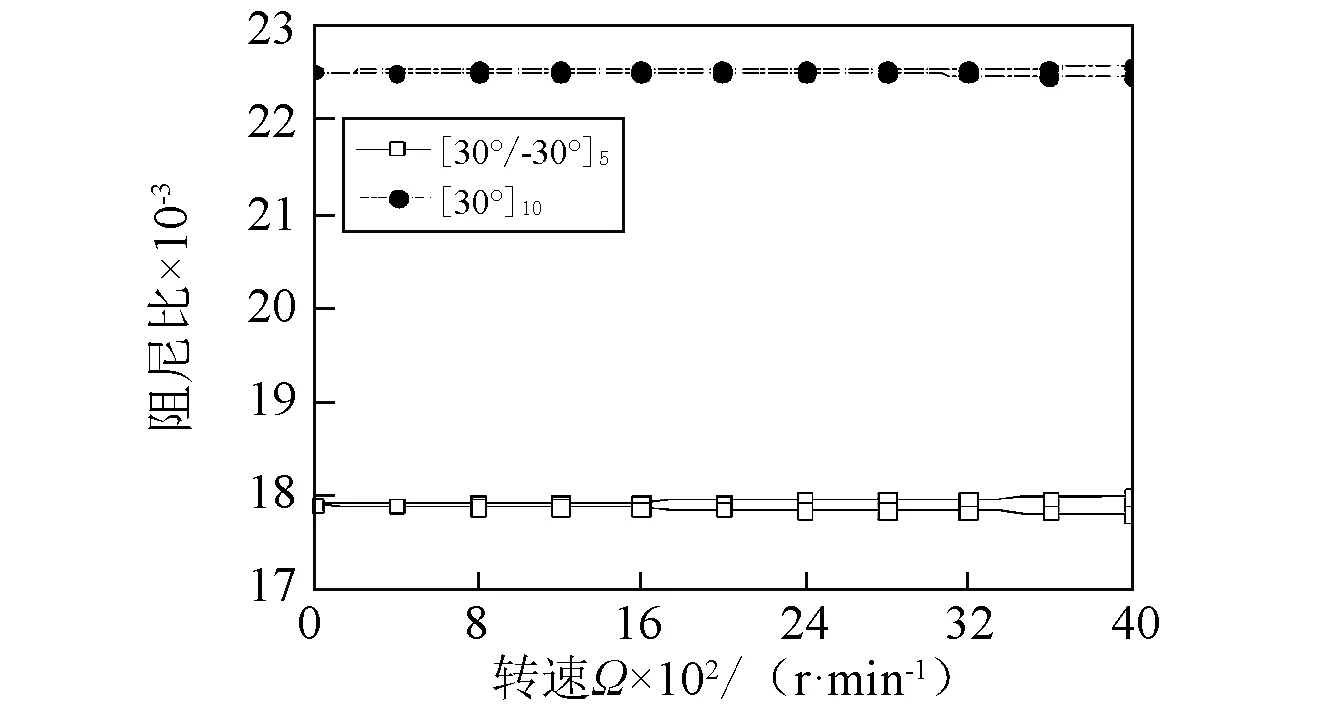
(b)阻尼比图7 不同铺层方式下复合材料轴固有频率和阻尼比随转速变化曲线( β=0°)Fig. 7 The natural frequency and damping ratio versus rotating speed Ω for various stacking sequences( β=0°)

图8(a)～图8(b)表示转速Ω=0时，对应于不同长径比固有频率和阻尼比随铺层角的变化曲线。结果表明，随着长径比的增大，固有频率和阻尼比随着长径比的增加逐渐减小，大长径比下的固有频率和阻尼比有彼此靠近的趋势，在这种情况下，铺层角的影响减弱。

图9(a)～图9(b)表示铺层角θ=60°时，不同长径比轴的固有频率和阻尼比随转速的变化曲线。结果表明，当长径比增至30和50时，上下两支的分叉现象相对不再明显。此外，随着长径比的增大，复合材料轴的固有频率值逐渐减小，且相互之间也在逐步靠近。这与图8(a)～图8(b)所得出的结论是相符合的。

2.1.4 黏弹性层剪切模量的影响

轴长L=1 m，共10层等厚，铺层方式[θ/-θ]5；约束层的的材料为高模碳/环氧, 共2层等厚，铺层方式[β/-β]，β=0°。黏弹性材料的剪切模量分别为Gv=(69×107)*(1+i)Pa、Gv=(69×106)*(1+i)Pa、Gv=(69×105)*(1+i)Pa、Gv=(69×104)*(1+i)Pa，ρv=1 575 kg/m3。

图10(a)～图10(b)表示转速Ω=0时，具有不同黏弹性材料剪切模量轴的固有频率和阻尼比随铺层角的变化曲线。结果表明，黏弹性材料剪切模量对复合材料轴的阻尼比有重要的影响，随着黏弹性材料剪切模量的增大，复合材料轴的固有频率也随之增大；但阻尼比似乎并非

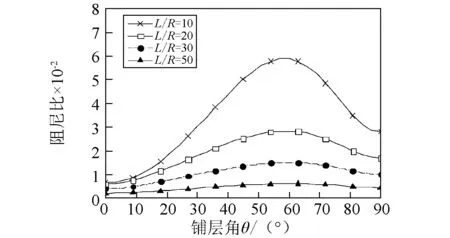
(b)阻尼比图8 不同长径比复合材料轴固有频率和阻尼比随铺层角变化曲线( β=0°)Fig.8 The natural frequency and damping ratio versus fiber angle θ for various ratio of the length and radius( β=0°)

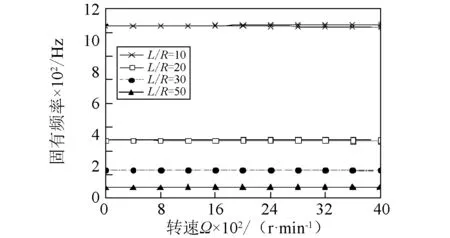
(a)固有频率

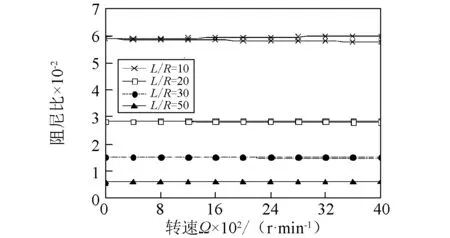
(b)阻尼比图9 不同长径比复合材料轴固有频率和阻尼比随转速变化曲线( β=0°)Fig. 9 The natural frequency and damping ratio versus rotating speed Ω for various ratio of the length and radius( β=0°)

随着黏弹性材料剪切模量的增大而单调地增大，当黏弹性材料剪切模量增加超过一定的限度，如图10(b) 中的Gv=(69×105)*(1+i)Pa，随着黏弹性材料剪切模量的继续增加，阻尼比反而会产生下降的趋势，这与文献[20]的研究发现是一致的。

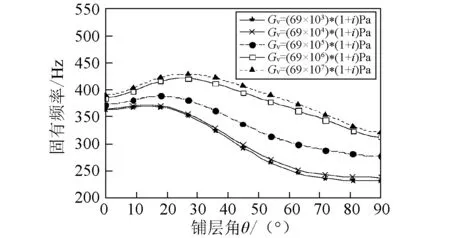
(a)固有频率

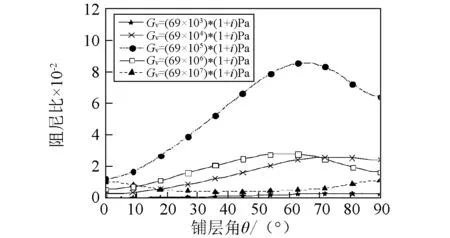
(b)阻尼比图10 不同黏弹性材料剪切模量的复合材料轴固有频率和阻尼比随铺层角θ变化曲线( β=0°)Fig. 10 The natural frequency and damping ratio versus fiber angle θ for various shear modulus of the viscoelastic material( β=0°)

图11(a)～图11(b)表示铺层角θ=60°时，具有不同黏弹性材料剪切模量轴的固有频率和阻尼比随转速的变化曲线。结果表明，黏弹性材料剪切模量大小的变化，对固有频率值影响不大，这与图14(a)～图14(b)的结果相一致。

图11(a)～图11(b)表示铺层角θ=60°时，具有不同黏弹性材料剪切模量轴的固有频率和阻尼比随转速的变化曲线。结果表明，当剪切模量超过Gv=(69×105)*(1+i)Pa时，阻尼比-转速曲线的上下两支的分叉相对不再明显。

2.2 自由振动时间响应

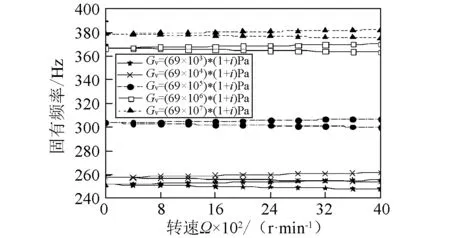
(a)固有频率

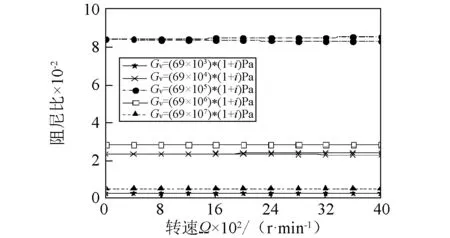
(b)阻尼比图11 不同黏弹性材料剪切模量的复合材料轴固有频率和阻尼比随转速Ω变化曲线( β=0°)Fig. 11 The natural frequency and damping ratio versus rotating speed Ω for various shear modulus of the viscoelastic material( β=0°)

采用四阶龙格-库塔法对振动方程进行数值积分，得到复合材料轴的跨截面中点位置分别沿y、z方向的时间响应曲线，研究约束层材料、轴的铺层方式、长径比以及黏弹性层剪切模量对自由振动响应特性的影响。

2.2.1 约束层材料的影响

复合材料轴、约束层和黏弹性层的参数和铺层与2.1.1中的取值相同，而轴的铺层角θ=60°，旋转速度Ω=2 000 r/min。

图12～图15分别表示约束层采用高模碳/环氧、石墨/环氧、钢和铝时，轴中点(x=L/2)的弯曲位移时间响应uy(L/2,t)和uz(L/2,t)。结果表明，在轴和约束层的铺层角一定的条件下，采用复合材料约束层，特别是高模量的碳纤维复合材料高模碳/环氧，能够获得比采用金属材料约束层更为优越的阻尼性能，这与图2的结论是一致的。

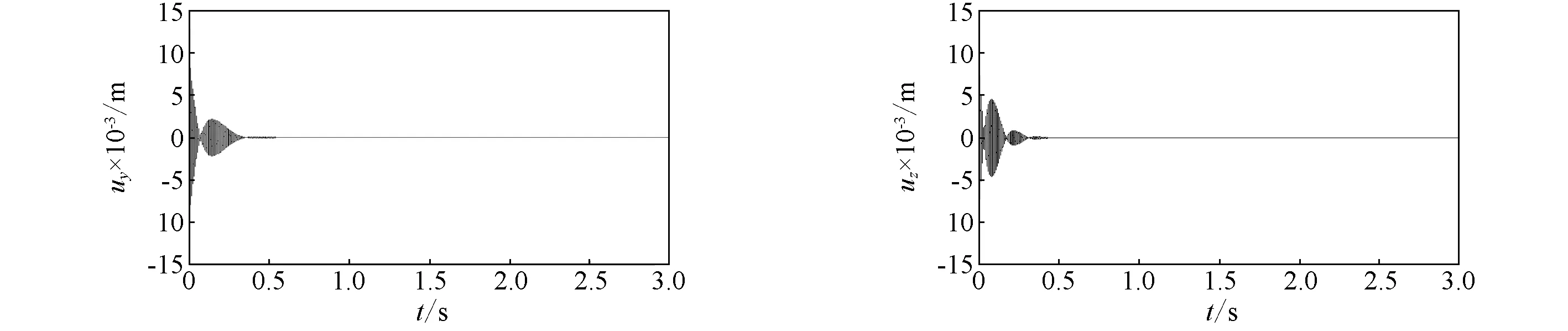
(a)y向时间响应 (b)z向时间响应图12 具有高模碳/环氧约束层的复合材料轴中点位移时间响应曲线Fig.12 Displacement response curves with time the composite shaft using HMCE constraining layer

(a)y向时间响应 (b)z向时间响应图13 具有石墨/环氧约束层的复合材料轴中点位移时间响应曲线Fig.13 Displacement response curves with time the composite shaft using graphite-epoxy constraining layer

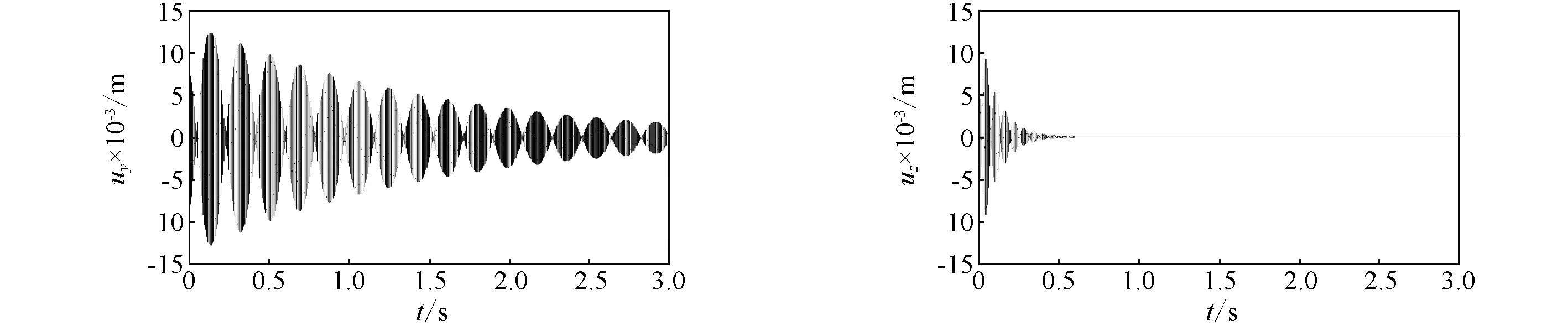
(a)y向时间响应 (b)z向时间响应图14 具有钢约束层的复合材料轴中点位移时间响应曲线Fig.14 Displacement response curves with time the composite shaft using steel constraining layer

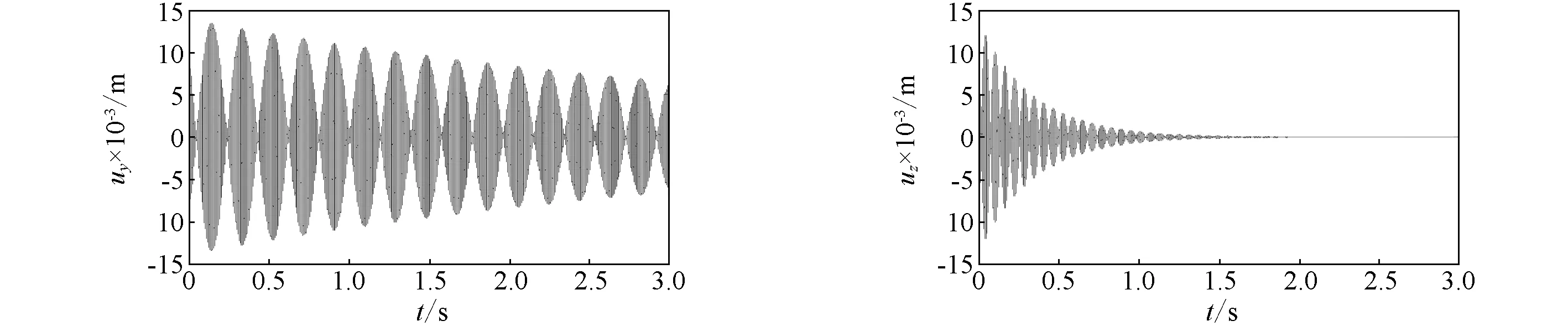
(a)y向时间响应 (b)z向时间响应图15 具有铝约束层的复合材料轴中点位移时间响应曲线Fig.15 Displacement response curves with time the composite shaft using aluminum constraining layer

2.2.2 轴的铺层方式的影响

复合材料轴、约束层和黏弹性层的参数和铺层与“2.1.2”中的取值相同，旋转速度Ω=2 000 r/min。图16～图17分别对应于采用两种不同的铺层方式， [40°/-40°]5和[40°]10，轴中点的弯曲位移时间响应。结果表明，复合材料轴在铺层方式[40°]10下的响应曲线比铺层方式[40°/-40°]5下的响应曲线，衰减速度要更快，这一结论与图6的结论是相对应的。

(a)y向时间响应 (b)z向时间响应图16 具有铺层方式[40°/-40°]5的复合材料轴中点位移时间响应曲线Fig.16 Displacement response curves with time the composite shaft with stacking sequence [40°/-40°]5

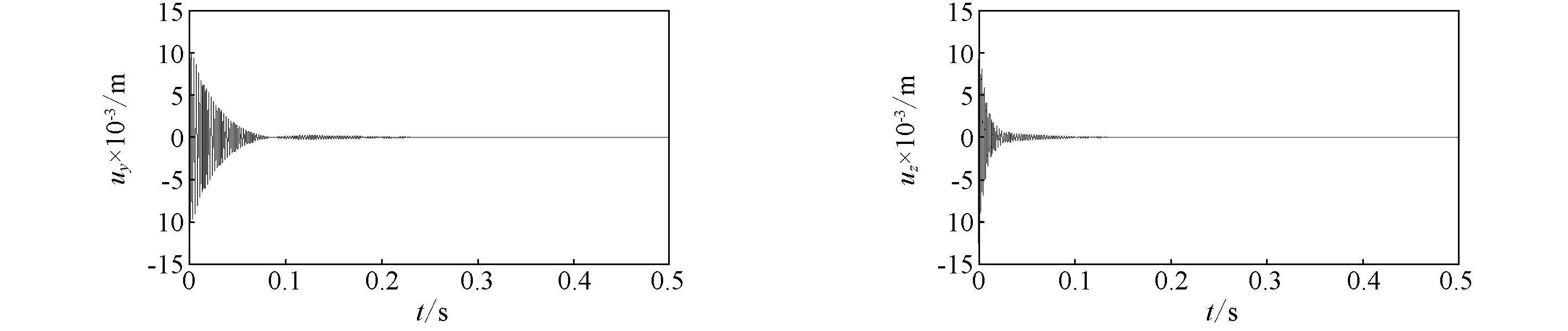
(a)y向时间响应 (b)z向时间响应图17 具有铺层方式[40°]10的复合材料轴中点位移时间响应曲线Fig.17 Displacement response curves with time the composite shaft with stacking sequence [40°]10

2.2.3 长径比的影响

复合材料轴、约束层和黏弹性层的参数和铺层与2.1.3中的取值相同，而轴的铺层角θ=60°，旋转速度Ω=2 000 r/min。图18～图20分别表示轴的长径比取10、20、50时，轴的弯曲位移时间响应。结果表明，短粗轴比细长轴的时间响应曲线衰减更快，因此，阻尼能力也更强，这也印证了图8的结果。

(a)y向时间响应 (b)z向时间响应图18 长径比为10的复合材料轴中点位移时间响应曲线Fig.18 Displacement response curves with time the composite shaft with the ratio of the length and radius 10

(a)y向时间响应 (b)z向时间响应图19 长径比为20的复合材料轴中点位移时间响应曲线Fig.19 Displacement response curves with time the composite shaft with the ratio of the length and radius 20

(a)y向时间响应 (b)z向时间响应图20 长径比为50的复合材料轴中点位移时间响应曲线Fig.20 Displacement response curves with time the composite shaft with the ratio of the length and radius 50

2.2.4 黏弹性层剪切模量的影响

复合材料轴、约束层和黏弹性层的参数和铺层与2.1.4中的取值相同，而轴的铺层角θ=60°，旋转速度Ω=2 000 r/min。图21～图23分别表示黏弹性材料的剪切模量分别为Gv=69×103(1+i)Pa，Gv=69×104(1+i)Pa和Gv=69×105(1+i)Pa时，轴的弯曲位移时间响应。结果表明，在一定的范围内，时间响应曲线的衰减速度随着黏弹性材料的剪切模量的增加而增加，这与图10的规律是一致的。

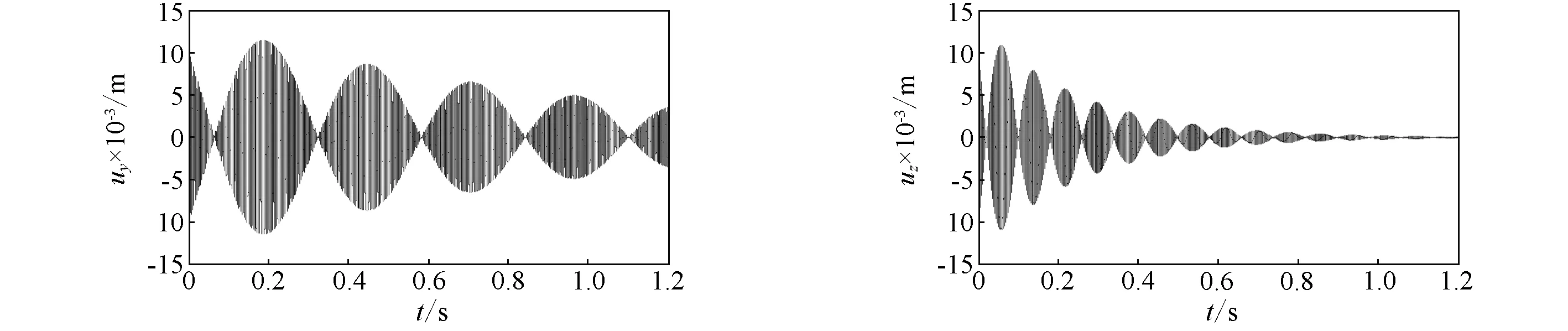
(a)y向时间响应 (b)z向时间响应图21 黏弹性层剪切模量Gv=69×103(1+i)Pa的复合材料轴中点位移时间响应曲线Fig.21 Displacement response curves with time the composite shaft with the shear modulus Gv=69×103(1+i)Pa

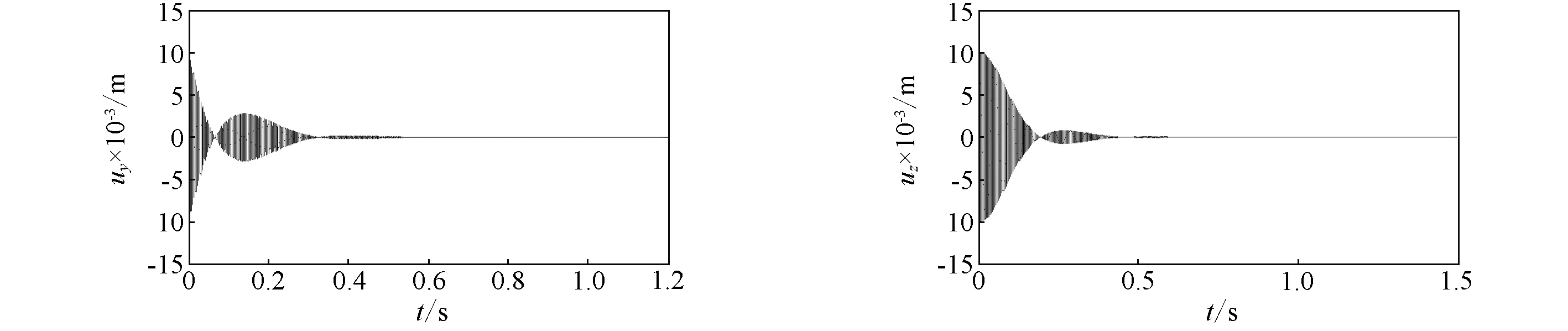
(a)y向时间响应 (b)z向时间响应图22 黏弹性层剪切模量Gv=69×104(1+i)Pa的复合材料轴中点位移时间响应曲线Fig.22 Displacement response curves with time the composite shaft with the shear modulus Gv=69×104(1+i)Pa

(a)y向时间响应 (b)z向时间响应图23 黏弹性层剪切模量Gv=69×105(1+i)Pa的复合材料轴中点位移时间响应曲线Fig.23 Displacement response curves with time the composite shaft with the shear modulus Gv=69×105(1+i)Pa

最后，值得注意的是，在上述不同参数影响下的时间响应曲线均出现了拍振现象。原因是在旋转状态下，由于陀螺矩阵的存在，使得轴在y和z方向上的振动产生相互耦合，从而产生拍振。显然，拍振频率随着转速的增加而增加。

3 结 论

本文采用复合材料轴、约束层和黏弹性层的应力应变本构关系、Timoshenko梁理论和Hamilton原理，建立具有约束层阻尼的复合材料轴的动力学方程。基于广义Galerkin法得到系统的离散化方程。采用特征值技术对上述方程进行求解，分析系统的固有振动特性(固有频率与阻尼比)。为了分析系统的自由振动时间响应特性，基于Raleigh假设，将比例阻尼矩阵引入系统的离散化方程，采用四阶龙格-库塔法进行数值积分。根据本文提出的模型与计算方法，针对不同的约束层材料、纤维铺层方式、长径比和黏弹性层剪切模量的复合材料轴，进行了固有频率、阻尼比和时间响应的计算。主要研究结论如下：

(1)复合材料约束层，特别是高模量碳纤维约束层与金属材料约束层相比，能够显著增加约束层阻尼复合材料传动轴的阻尼能力，同时不会以减低结构本身的固有频率为代价。

(2)复合材料轴铺层方式能够对轴的固有频率与阻尼比产生不容忽视的影响。

(3)增大复合材料轴的长径比，其固有频率值和阻尼比均随之减小。

(4)复合材料轴的固有频率随着黏弹性材料剪切模量的增加而增加，在一定的范围内，黏弹性材料剪切模量的增加将导致复合材料轴的阻尼比增加，当黏弹性材料剪切模量增加超出一定限度，复合材料轴的阻尼比随着黏弹性材料剪切模量的增加而减小。

(5)轴的旋转效应对复合材料轴的振动特性能够带来明显的影响，例如，转速的增加会导致固有频率和阻尼比出现分叉现象，旋转状态下的自由振动时间响应会发生拍振现象。

本文的研究可进一步扩展，研究部分粘贴约束阻尼层的旋转复合材料轴的动力学特性、考虑黏弹性材料频变特性，以及考虑复合材料内阻的旋转复合材料轴的动力稳定性问题。

[ 1 ] HETHERINGTON E L, KRAUS R E, DARLOW M S. Demonstration of a super critical composite helicopter power transmission shaft [J]. Journal of American Helicopter Society, 1990, 35(1): 23-28.

[ 2 ] DARLOW M S, CREONTE J. Optimal design of composite helicopter power transmission shafts with axially varying fiber lay-up[J]. Journal of the American Helicopter Society,1995,40(2):50-56.

[ 3 ] LEE D G,KIM H S,KIM J W,et al. Design and manufacture of an automotive hybrid aluminum/composite drive shaft[J].Composite Structures,2004,63(1):87-99.

[ 4 ] TALIB A R A,ALI A, BADIE M A,et al. Developing a hybrid,carbon/glass fiber-reinforced,epoxy composite automotive drive shaft[J].Materials and Design,2010,31(1):514-521.

[ 5 ] BADIE M A, MAHDI E, HAMOUDA A M S.An investigation into hybrid carbon/glass fiber reinforced epoxy composite automotive drive shaft[J].Materials and Design, 2011,32(3):1485-1500.

[ 6 ] 戴德沛.阻尼技术的工程应用[M]. 北京：清华大学出版社，1991.

[ 7 ] ROSS D, UNGAR E E, KERWIN E M. Damping of plate flexural vibrations by means of viscoelastic laminate[M].Oxford:Pergamon Press, 1959.

[ 8 ] DITARANTO R A. Theory of vibratory bending for elastic and viscoelastic layered finite-length beams[J]. Journal of Applied Mechanics,1965, 32(4):881-886.

[ 9 ] MEAD D J, MARKUS S. The forced vibrations of a three-layer damped sandwich beam with arbitrary boundary conditions[J]. Journal of Sound & Vibration,1969, 10(2):163-175.

[10] KERWIN E M. Damping of flexural waves by a constrained viscoelastic layer [J]. Journal of the Acoustical Society of America, 1959, 31(7): 952-962.

[11] CHEN Y C, HUANG S C. An optimal placement of CLD treatment for vibration suppression of plates[J]. International Journal of Mechanical Sciences, 2002, 44(8):1801-1821.

[12] DITARANTO R A. Theory of vibratory bending for elastic and viscoelastic layered finite-length beams[J]. Journal of Applied Mechanics,1965,32(4):881-886.

[13] MEAD, D J, MARKUS S. The forced vibration of a three-layer damping sandwich beam with arbitrary boundary conditions [J]. Journal of Sound and Vibration, 1969, 10(2): 163-175.

[14] NAPOLITANO K L, GRIPPO W, KOSMATKA J B, et al. A comparison of two cocured damped composite torsion shafts [J]. Composite Structures, 1998, 43(2): 115-125.

[15] VENKATACHALAM R, PRABU S B. Vibration characteristics of orthotropic shaft-disk system with different constrained damping layers: experimental and numerical study [J].International Journal of Advanced Manufacturing Technology, 2013, 65: 601-610.

[16] GHONEIM H, LAWRIE D J. Analysis of the flexural vibration of a composite drive shaft with partial cylindrical constrained layer damping treatment[J].Journal of Vibration and Control,2006,12(1):25-55.

[17] REN Yongsheng,ZHANG Yuhuan. Free vibration and damping of rotating composite shaft with a constrained layer damping[J]. Shock and Vibration, 2016(4):1-20

[18] DHARMARAJAN S, MCCUTCHEN H. Shear coefficients for orthotropic beams[J].Journal of Composite Materials,1973,7(4):530-535.

[19] KIM W, ARGENTO A, SCOTT R A. Free vibration of a rotating tapered composite Timoshenko shaft[J]. Journal of Sound and Vibration,1999,226(1):125-147.

[20] JIN G Y, YANG C M, LIU Z G, et al. A unified method for the vibration and damping analysis of constrained layer damping cylindrical shells with arbitrary boundary conditions[J]. Composite Structures,2015, 130:124-142.

Vibration characteristics of a rotating composite shaft with constrained layer damping

SHI Yuyan, REN Yongsheng, ZHANG Yuhuan

(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qindao 266590, China)

The vibration suppression of a composite shaft operating at high speeds is an important issue in structural design of advance power transmission of helicopters and automobiles. Constrained layer damping technology is an effective method in engineering field and it is widely used for reducing structural vibration. However, the studies on strengthening damping of a composite shaft by using constrained layer damping treatment are relatively few. Here, a mechanical model was developed for a rotating composite shaft with passive constrained layer damping (PCLD). Based on the constitutive relation of materials and the strain-displacement relation, the kinetic energy and strain energy of the composite shaft, constrained layer and viscoelastic layer were derived. Hamilton’s principle was used to derive the motion equations of the shaft with PCLD. The motion equations were discretized by using the general Galerkin method. The natural frequencies and modal damping ratios were obtained by computing a matrix eigenvalue problem. Using the assumption of proportional damping and Runge-Kutta integration algorithm, the time history responses of the system’s damped free vibration were gained. The effects of constrained layer material, viscoelastic layer material, stacking sequences, ratio of length to diameter and rotating speed on the natural vibration characteristics and damped free vibration responses of the composite shaft with PCLD were analyzed using numerical simulation.

passive constrained layer damping (PCLD); composite shaft; rotor system; damped free vibration

国家自然科学基金(11272190)

2016-06-29 修改稿收到日期：2016-08-31

时玉艳 女，硕士生，1989年生

任勇生 男，博士，教授，1956年生

TB33

A

10.13465/j.cnki.jvs.2017.07.008