从三角形重心定理到“共点三线通式”探索

安徽省黄山旅游管理学校(245700)

吴灵捷●

从三角形重心定理到“共点三线通式”探索

安徽省黄山旅游管理学校(245700)

吴灵捷●

笔者在讲授三角形的重心定理时，无意间发现了重心、内心之间具有一条共同性质，下面就是这个通式发现过程.

重心定理 三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍.

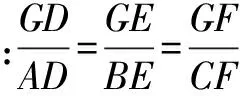
将重心定理公式变形为：

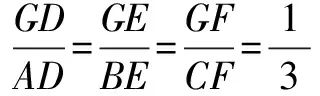
故可以得：

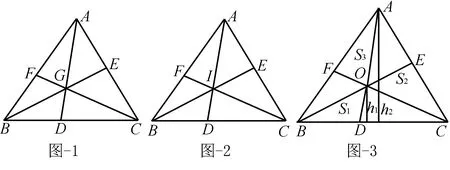
证 ∵点I是内心,

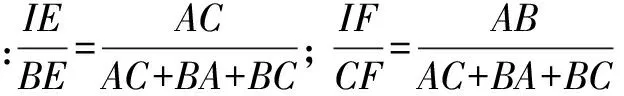
猜想：既然三角形的重心、内心具有这样的性质，那么三角形的垂心、外心是否具有这个性质呢？如果再推广到一般的形态，会是什么情况.

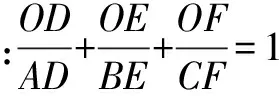
证明 如图3，令S△ABC=S；S△BOC=S1；S△COA=S2；S△AOB=S3.

令△ABC中BC边上的高为ha；△ABC中AC边上的高为hb；△ABC中AB边上的高为hc；△BOC中BC边上的高为h1；△COA中AC边上的高为h2；△AOB中AB边上的高为h3.

由相似三角形的知识可知：

∵S△ABC=S△BOC+S△COA+S△AOB

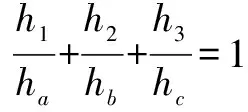
上述证明就给了三角形内任意一点都满足该性质，因此三角形的垂心、内心也具有该性质.

▶开口向上，对称轴为x=0.则当x<0时函数值y随x的增大而减小.当m=2时，原函数y=x2-2x-3的图象开口向上，对称轴为x=1.则当x<1时函数值y随x的增大而减小.

此题解答过程看似复杂，但是只要捋清思路，逐步地分情况讨论，实际题目难度并不是很高，并且通过对图象的想象，可以帮助我们更快地解决问题.此题第一问是对于函数图象开口方向、坐标位置导致其与x轴存在交点的问题，这种题目无论如何变化只有三种情况：①顶点在x轴上，无论开口方向如何函数与x轴有且只有一个交点；②顶点在x轴上方，开口向下才与x轴有交点；③顶点在x轴下方，开口向上才与x轴有交点.第二问是对函数单调性的讨论，在目前阶段的二次函数学习中函数的单调性只有在顶点处会发生改变，在今后还会接触到带有绝对值符号的二次函数，目前暂不讨论.

在做此题的时候学生们经常在m值的讨论以及B点坐标的确认方面出错误，对于这种解答结果偏多，需要同学们根据条件筛选结果，或者根据不同条件分组讨论的时候，我建议同学们画出解析式的示意图帮助自己理解，对于分情况讨论的时候可以画出多组图形，以免混淆.往往这种分情况讨论的题目，每种情况的难度并不大，但是需要同学们一定要思路清晰逻辑缜密，不要遗漏.

由于篇幅有限，二次函数教学中的难点与易错点先为大家介绍到这里，二次函数的教学中仍有很多难点在此虽未介绍，但是依然很重要，希望广大的师生朋友们在二次函数的学习过程中加以重视，多学多练.

[1]王礼儿.一元二次函数教学过程中的难点分析[J].读书文摘，2015(12).

[2]张文彬.二次函数与一元二次方程关系案例与反思[J].科技咨询：教育科技，2015(2).

G632

B

1008-0333(2017)08-0033-01