由《等腰三角形的性质》谈数学导学案的问题设置

安徽省颍上县五十铺乡中心学校(236219)

吴明辉●

由《等腰三角形的性质》谈数学导学案的问题设置

安徽省颍上县五十铺乡中心学校(236219)

吴明辉●

数学导学案是把知识问题化，学生在处理问题时，掌握相关知识，发展各种技能.因此，要精心创设各种教学情境，设置科学合理的数学问题，才能激发学生学习数学的好奇心和学习数学的兴趣.

数学导学案;问题设置

本文以《等腰三角形的性质》这节课，谈谈对数学导学案中问题设置的看法.

一、数学导学案的问题设置要生活化

数学是生活中的一份子，它存在于生活中，离开了生活，数学将是一片死海，没有生活的数学就是没有魅力的数学.同时，《新课标》指出应该将数学教学活动作为挖掘学生好奇心的基础，通过将数学知识同学生的实际生活结合起来，来增加数学课程的现实感.所以，教师在设计教学导学案时，应该注重按照学生感兴趣的生活话题来进行设计，帮助有效激发学生好奇心，增加学习兴趣.

二、数学导学案的问题设置要有实验性

根据教学内容设计易于操作的实验性的问题，可降低学习中抽象性的难度，让学生在实验中领悟数学的本质.

问题1：任意画一个等腰三角形，把刚画好的等腰三角形ABC的两腰重叠在一起折叠，折痕为AD，然后展平.根据实验，你发现等腰三角形具有怎样的对称性？

学生在动手实验的过程中感受到等腰三角形是轴对称图形，并能初步感知等腰三角形性质，为下一步探讨性质埋下伏笔.

三、数学导学案的问题设置要有层次性

《数学课程标准》 规定：“让不同的人在 数学上得到不同的发展.”学生是一个个活生生的生命体，生命之间必然存在许多差异.数学课堂首先应该承认并尊重每位同学们之间的差异.在任何一个班集体中，学生的智力水平和学习能力也都是存在差异的.

问题2：通过以上的实验，结合图1，思考下列问题：

1.你能找出图中哪些相等的线段和相等的角？

2.折痕AD为等腰三角形ABC的什么线？

3.归纳等腰三角形有什么样的性质？

第一个问题以等腰三角形的轴对称性为切入点，学生通过折叠发现各种等量关系.第二个问题围绕探求折痕AD的多重“身份”展开讨论，得到关于折痕AD的性质.第三个问题归纳整理得出等腰三角形的两个性质.三个问题不仅激发了学生学习的兴趣和求知欲，而且问题的梯度拾级而上，这种逐步深入，具有层次性的问题，符合学生的认知规律．

四、数学导学案的问题设置要有拓展性

数学学习的本质是用所学的知识解决问题，是对知识的再创造.因此在导学案的设计中，设计的问题要有拓展性.

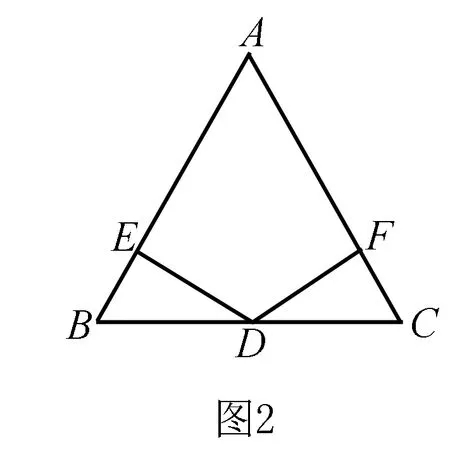
问题3 如图2，在△ABC中，AB=AC，D是BC边上的一点，DE⊥AB，DF⊥AC，垂足分别为E，F.

1.若不能添辅助线，你会添加一个怎样的条件，使DE=DF.(添加BD=CD，或BE=CF均能证明△BDE≌△CDF)

2.若添辅助线，你会添加一个怎样的条件，使DE=DF.

(连结AD，添加BD=CD，利用等腰三角形三线合一得出AD平分∠BAC，由角平分线上的点到角的两边距离相等得到DE=DF)

此问题是为使学生巩固等腰三角形的性质而增设，也可通过构造三角形全等的角度证得，通过这种具有拓展性的问题，达到拓宽学生分析问题的视野和思路.

五、数学导学案的问题设置的几点思考

1.数学导学案中的问题情境，其实就是一种思维活动.数学思维活动主要表现在解决问题的过程中.探究开始于问题，问题产生于情境.所以教师应该善于捕捉学生的生活情境，也就是找准“最近发展区”.教师应该经常设置多种问题情境，为学生的认知制造意识冲突，提升学生的问题意识.在进行教学导学案设计时，首先应该明确教学目的，根据课程需求来设置一定的问题情景.在这个过程中应该注意克服课堂教学的随意性，把控教学重点，设置问题情境时，要保证具有代表性、 典型性，问题的形式要灵活、有趣味，具有针对性.为了达到良好的效果，还要保证设计的问题能够符合逻辑，能够环环相扣，增加问题之间的紧密联系.为了达此目的，教师应该能够掌握学生的固有认知同新认知的矛盾，要善于引导学生随时发现问题，解决问题.

2.转变对教材的认识.数学教材只是数学知识的载体，它是数学导学案中问题设置的依据，教师从事教学，不是教教材，而是用教材教.数学教材是一条知识的线索，它的功能是为学生的学习提供一个路径.教材上的素材，是可以改变的，这也正是教学创造性得以产生的重要原因.所以教师要全方位地解读教材，理解教材；要多角度地分析教材，钻研教材.掌握作者的编写意图，深入了解知识体系，并因材施教，这样才能设计出科学合理的、符合学生实际特点的数学问题．

3.通过数学导学案的问题，培养学生的数学思想方法.作为教师，在教学期间，应该将眼界放宽，不要着眼于某一个数学问题的解决，应该善于发掘在该问题当中存在着的数学思想方法，那么该如何利用导学案中的教学问题，来挖掘存在于问题当中的数学思想方法呢？

数学导学案中问题的设置，不应该局限于掌握新知和对常规问题的解决，应设置具有实验、归纳、猜想、类比、推理的问题，从一步一步地探究当中来调动学生的学习积极性和主动性，使课堂效率最大化.

[1]王淑清，柳丽红.数学教学研究与实践[M].太原：山西科学技术出版社.

[2]张绪培.初中数学教学案例专题研究[M].杭州：浙江大学出版社.

[3]张仁贤.名师谈高效课堂[M].北京：中国轻工业出版社.

G632

B

1008-0333(2017)08-0029-01