例析二次函数教学难点与习题易错点
2017-04-14福建省泉州现代中学362000
福建省泉州现代中学(362000)
娄丽凤●
例析二次函数教学难点与习题易错点
福建省泉州现代中学(362000)
娄丽凤●
二次函数作为初中数学教学的重要知识,同时也是中考的必考考点之一,一直广泛地受到初中教育同人们的高度重视.二次函数作为学生初步接触高阶函数的门户,有着十分重要的意义,无论是在解题方法还是在思维逻辑的培养上都对学生将来数学思维的发展有着十分决定性的作用.因此,在二次函数的教学过程中一定要注意教学方式、方法以及针对于二次函数的数学思维的培养,这不仅有利于学生的学习理解,同时也对将来学生学习更高阶的函数知识有很大的帮助.
初中数学;二次函数;初中教学
二次函数相对于一次函数无论是在解析式上还是在图形上都有着很大的变化,并且二次函数的解析式有着更多的变化形式,不同的变化形式又有着不同的作用,相对于过去学习的一次函数而言,二次函数对于数形结合有着更高的要求,并且抛物线的图形相对于直线也有着很强的特殊性.
一、函数解析式的不同表达形式
作为图形的基础,解析式的表达方式的不同虽然不会影响图形的形状,但是不同的解析式的表达形式有着各自不同的侧重点,这就要求学生们在学习的过程中一定要熟练、灵活地掌握.
1.一般式:这种形式的解析式形如:y=ax2+bx+c,是将x按照从高到低的顺序降幂排列,解析式在题目的题干中经常可见.该式中需要注意的是a≠0,a值的正负影响抛物线的开口方向.
2.顶点式:这种形式的解析式形如:y=a(x-h)2+k,该式十分利于数形结合确定抛物线的顶点,该式顶点坐标即为(h,k).该式中a≠0,同样a值正负影响抛物线开口方向.因此已知顶点坐标和抛物线上任意一点坐标时用此式可以十分方便的求出抛物线的解析式.该式中a≠0,同样a值正负影响抛物线开口方向.
3.双根式:这种形式的解析式形如y=a(x-x1)(x-x2),该式利于寻找抛物线与x轴的交点,交点坐标即为(x1,0)与(x2,0).
二、函数与方程的关系与差别
对于已经学习过一元二次方程的同学们来说,最常见的问题就是将一元二次方程与二次函数相混淆.不过,二次函数与一元二次方程的确有着十分密切地联系,在二次函数的学习中我们也经常需要应用到一元二次方程,尤其是在求抛物线与x轴交点的时候,需要用到一些与一元二次方程相关的知识.
例题1 已知二次函数y=x2-x+m.
(1)求该函数的顶点坐标以及对称轴;
(2)已知此函数图象与y轴存在交点A,过A点作直线AB,且AB与x轴平行,B点为该直线与函数图象的另一交点,当S△AOB=4时,求二次函数的解析式.
(2)由于AB∥x轴,∴A点与B点的纵坐标相等.
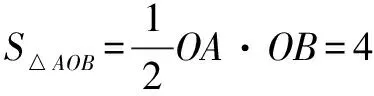
因此二次函数的解析式为y=x2-x+8或y=x2-x-8.
此题就是一道将二次函数与一元二次方程相结合的题目,同学们在解答此题的过程中需要清晰地明白各个条件所给目的以及如何应用,并且对于二次函数与一元二次方程的关系要掌握牢固,此题第一问很容易解答,是一道基础题,而第二问则需要同学们对函数解析式、点坐标的含义、图形与坐标的关系等知识都熟练掌握.
同学们在解答此题时最大的障碍就是对于坐标的解读与三角形面积条件的解读,而最常出现的问题则是主要集中m值的正负上.由于现阶段所学面积的大小是不涉及坐标正负的,因此在解答一些涉及到面积问题的题目时一定要注意正负两种情况.
三、单调性问题
在过去学习一次函数时,函数的单调性是绝对的,并无变化,但是在二次函数中,函数的单调性是会改变的,并且从此开始,单调性、顶点、斜率等等函数的特征也逐步呈现在学生们的眼前,因此二次函数的单调性是初中数学教学的一项重点,因此在各种题目中也是屡见不鲜.


分情况讨论:当m=0时,原函数y=x2-1的图象
▶
G632
B
1008-0333(2017)08-0032-02
