旋转自由摆的控制方法研究

胡建秋，毛丽民，卢振利，2，朱培逸

（1.常熟理工学院电气与自动化工程学院，江苏 常熟 215500；2.阿威罗大学电子和信息通信工程研究所，阿威罗 3810-193，葡萄牙）

旋转自由摆的控制方法研究

胡建秋1，毛丽民1，卢振利1，2，朱培逸1

（1.常熟理工学院电气与自动化工程学院，江苏 常熟 215500；2.阿威罗大学电子和信息通信工程研究所，阿威罗 3810-193，葡萄牙）

选取旋转自由摆作为研究对象，建立了系统的数学模型，分析并验证了系统的稳定性和可控可观性.在此基础上，提出了一种基于STM32的实验硬件平台，该平台采用步进电机驱动自由摆的旋转，利用光电编码器测量摆杆的旋转角度，通过PID控制算法实现自由摆的运动控制，对自由摆的起摆、摆起稳定、镇定进行了分析.实验表明，本文采用的旋转自由摆控制方法，使自由摆运行稳定，具有一定的抗干扰能力.

自由摆；PID；STM32；MATLAB/Simulink仿真

自20世纪50年代以来，为了解决航空航天飞行过程中对姿态的调整及平衡控制，双足机器人的直立行走等问题，开始研究分析自由摆系统，国内外已有一定成果.由于自由摆参数复杂，同时受外界不确定因素的干扰，具有很强的不确定性［1］.目前，市面上有不同类型的自由摆实验平台，例如固高公司开发的自由摆，有环形自由摆、直线自由摆、平面自由摆［2］.但这类自由摆价格高昂，二次开发困难.本文以自制旋转自由摆为实验平台，验证控制方法，更适合一般教学与研究.

1 自由摆控制系统的方案设计

本文的旋转自由摆以STM32为控制核心，步进电机提供动力，光电编码器进行角度的测试，通过PID控制算法，实现自由摆摆杆的起摆，稳定，镇定的控制.总体设计如图1所示.

旋转自由摆系统主要由控制器、支架、摆杆、旋转臂、光电编码器、步进电动机、电机驱动、支撑轴承、自由摆底座等构成［3］，如图2所示.由图2可以看出，旋臂上安装光电编码器，光电编码器通过方波脉冲判断旋转方向.首先进行基准定位，利用PID控制算法，捕捉定点，然后通过摆杆惯性起摆，保持稳定［4］.

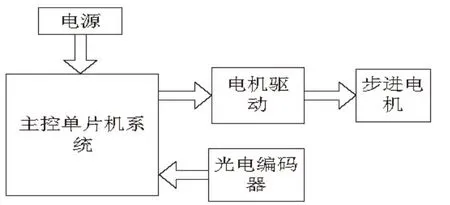
图1 系统的总体设计框图

图2 旋转自由摆系统结构示意图

2 旋转自由摆的数学模型

在忽略摩擦影响的情况下，自由摆的力学分析如图3所示.对自由摆摆杆，在非惯性系o2-x2-y2中有

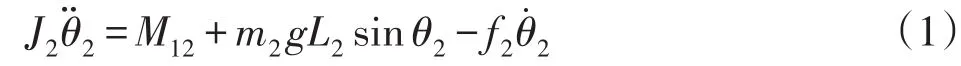
式中，J2为转动惯量，M12为旋臂对摆杆力矩（惯性力矩）.有

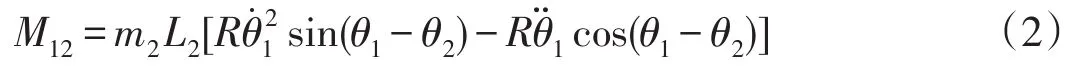
对于旋臂，在惯性系o1-x1-y1中，有

其中，J1为转动惯量，M0为电机输出转矩，有

M21为旋臂对摆杆的力矩，利用反作用力，有

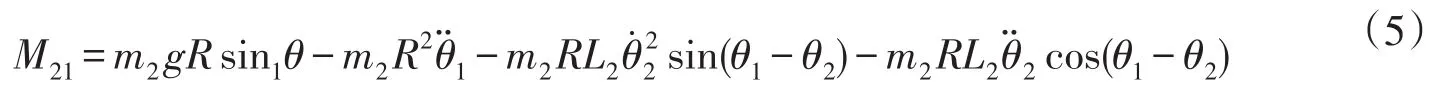
联立方程式(1)～(5)，得非线性数学模型为

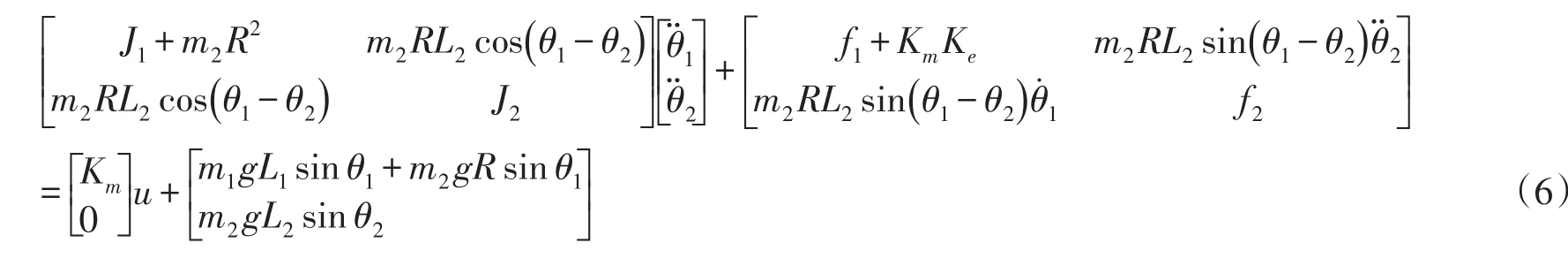
根据非线性模型，令θ1→0，θ2→0，则线性化模型为

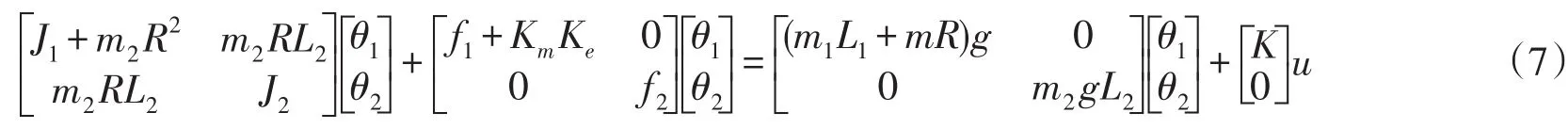
显然，自由摆系统是非线性系统，通过实验及计算，可得到各个机械参数值.

其中

分析A、B、C这3个矩阵，判断自由摆系统性能，可知该系统完全能控能观，但是不稳定的.

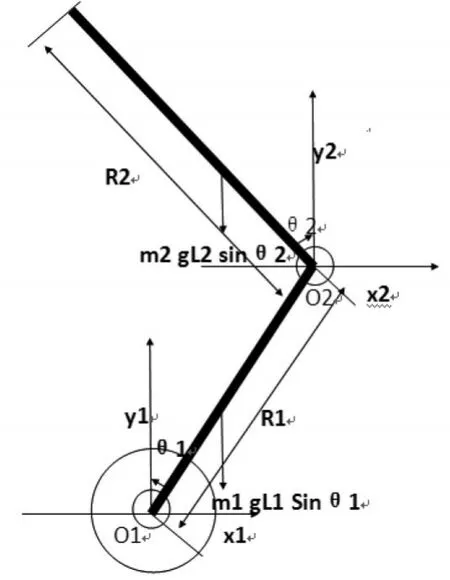
图3 自由摆模型

3 自由摆控制方法分析

自由摆控制的总体流程如图4所示.系统启动，进行初始化，为编码器采样，电动机控制，PID控制做准备.在电机的驱动下，自由摆系统进行起摆，起摆主要是能量控制.具体的起摆方法是数学模型法、急停法、惯性法等.数学模型法比较精确，但计算复杂，只适合大型系统.急停法能让摆杆瞬间到达顶端，但主要依赖经验模型，易产生机械磨损和系统不稳定.惯性法通用性较好，电动机以中等速度做往复运动，当摆杆往顶端运动，电动机保持通电以靠近顶端，一旦摆杆靠近顶端，电动机就保持断电，充分利用摆杆惯性保持系统平滑［5］.

本系统每隔1.2 ms进行一次数据采样，记录定位摆杆的位置（最主要是摆杆在顶端的定位），并进行控制，同时也能抵抗抖动与外界干扰.传统自由摆是每采样一次就进行一次点击控制，易出现不能及时处理摆杆运动与识别干扰问题.

本文将摆杆顶端区域位置分为3部分：摆杆顶端区域为-15°～15°，理想倒立状态是0°，自然状态下是180°.当编码器采集到摆杆相应数据后，判断系统是否进入顶端区域.若没有进入顶端区域，就再进行摆杆采样.

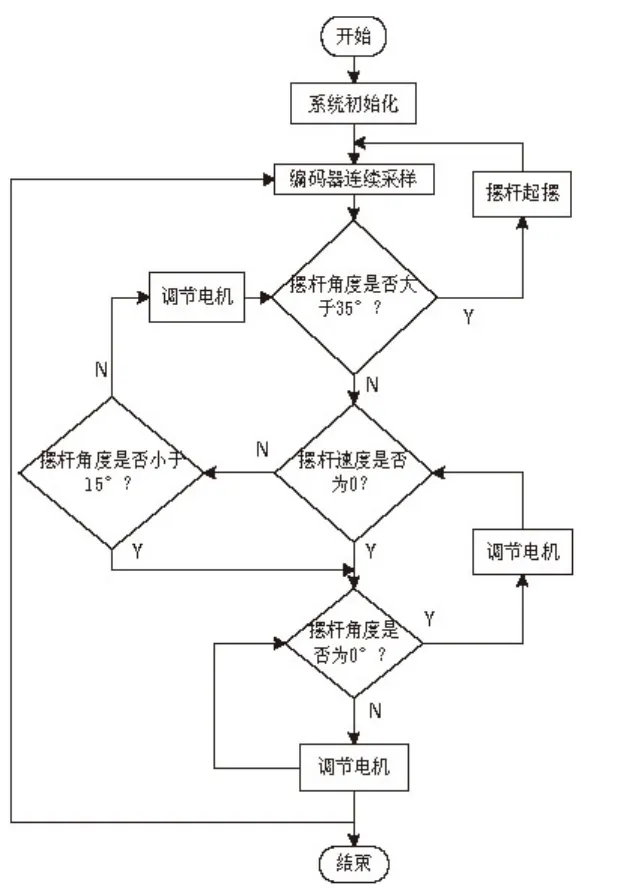
图4 自由摆控制流程图

4 PID控制算法的实现

4.1 PID控制概述

PID控制是最常用的控制算法，其原理简单，应用范围广，适用性强，易于掌握［7］.PID控制框图如图5所示.

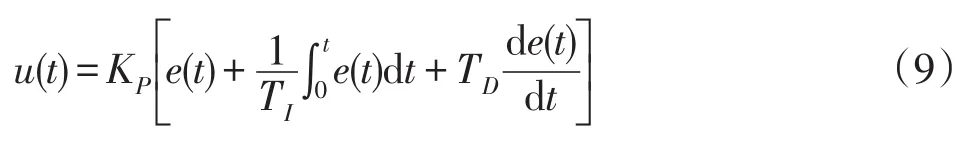
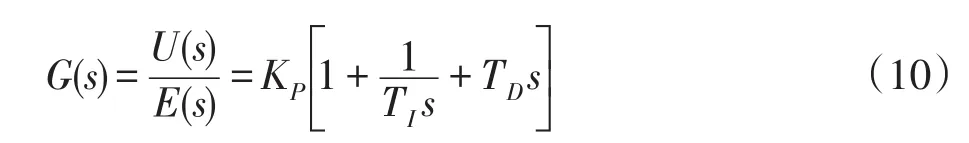
由于纯微分环节物理上实际是无法实现的，实际中应用的模拟PID控制传递函数是带有惯性的PID控制.即

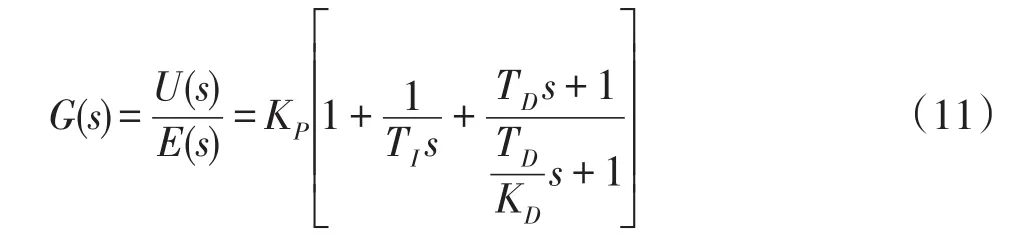
4.2 自由摆起摆过程实现

本文先设置摆杆很小的误差角，使其自动起摆，当摆杆摆到此次最高点时，旋转臂突然反向加速，摆杆每到一次最高点便可获得一些额外的动能.当往返运动的次数达到一定值时，摆杆累积足够的能量摆到顶端［8］.本文采用积分分离式的PID控制算法，当摆杆的位置接近目标值时，积分作用才起作用，摆杆的加速度随着摆杆幅度的增大逐渐减小，帮助摆杆平稳过渡到下一状态，有效降低系统的振荡.自由摆起摆流程如图6所示，以下为部分PID算法软件程序及解释.

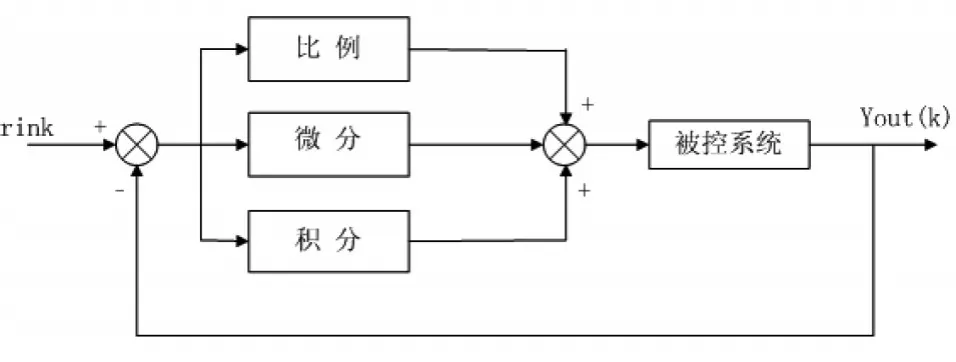
图5 PID控制系统框图

4.3 自由摆摆起稳定过程实现

考虑到摆杆从底部加速摆到顶端，速度较大，增加了摆杆摆动失败的概率.在诸多的不确定因数下，对顶部的平衡性能要求苛刻，不易实现.因此本文在摆杆起摆和保持平衡的过程中，插入一个减速缓冲过程.根据摆杆的速度，动态调整电机的转向、转速，使摆杆的速度能够在最短时间内降到0，从而和保持平衡的过程衔接.这个过程对整个系统的稳定起着至关重要的作用，也是自由摆能否成功摆起的关键［9］.自由摆摆起到稳定过程流程如图7所示.以下为自由摆摆起到稳定过程的部分程序.

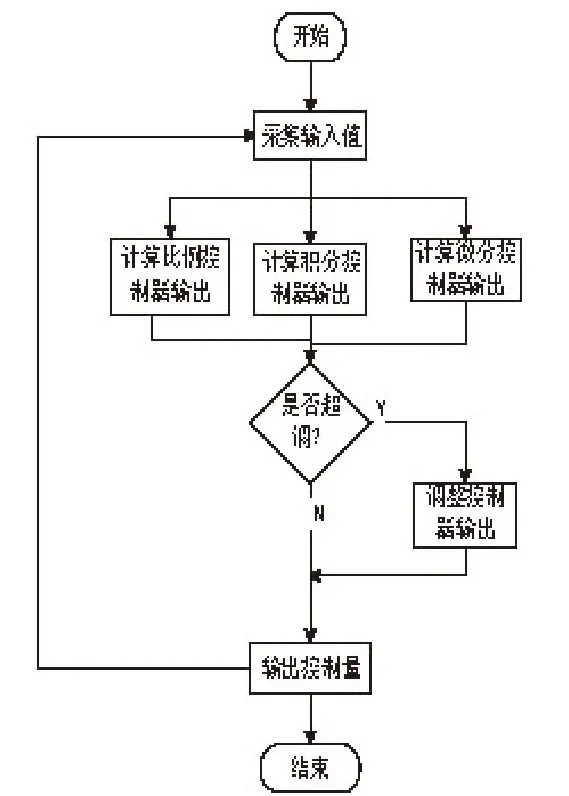
图7 自由摆摆起稳定过程流程图

4.4 自由摆镇定控制实现

该过程主要把摆杆快速、平稳地稳定在旋转臂上.该系统使用步进电机，在旋转时本身就会产生较大的振动，尤其在转向和速度变换频繁的情况下，干扰更加明显.因此，借鉴模糊控制的思想，在顶端平衡时设置了两个规则，分别在摆杆处于不同位置采用不同的规则加以控制，同时使用加权取点采样的方法，对编码器的数值进行采样，两者相辅，成功解决了步进电机的抖动问题.当系统发生一些小振荡时不至于发散，当靠近顶端稳定时，电机能急速停止，并较好地稳定下来.自由摆镇定流程如图8所示.

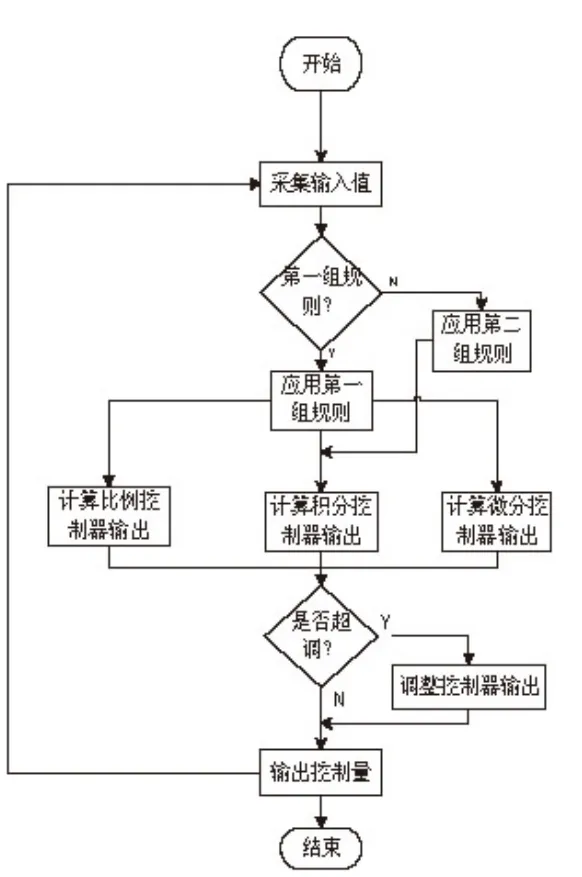
图8 自由摆镇定流程图

根据自由摆镇定控制的方法，制定规则的条件值，根据达到条件值执行相应的动作.

以上为自由摆系统起摆到达稳定部分的PID算法的计算，主要通过计算出的误差控制自由摆的摆动角度范围.

5 倒立摆的仿真实验

系统PID调节器的阶跃调试，将自由摆系统的PID参数调整到一个适宜的状态.相同阶跃信号作用下，用不同PID参数，得到不同的阶跃响应曲线［10］.设系统模型为，闭环系统阶跃响应如图9所示.

图10给出同一被控对象在相同阶跃输入下，用不同调节器的阶跃响应曲线.系统模型仍然是，闭环系统阶跃响应波形如图10所示.

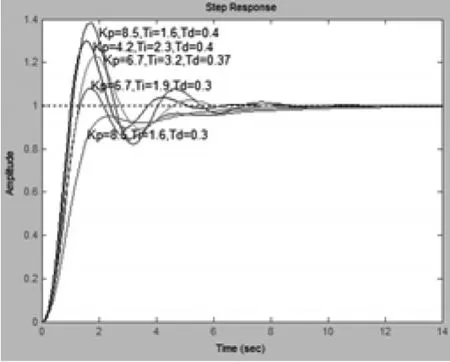
图9 不同参数下阶跃响应曲线

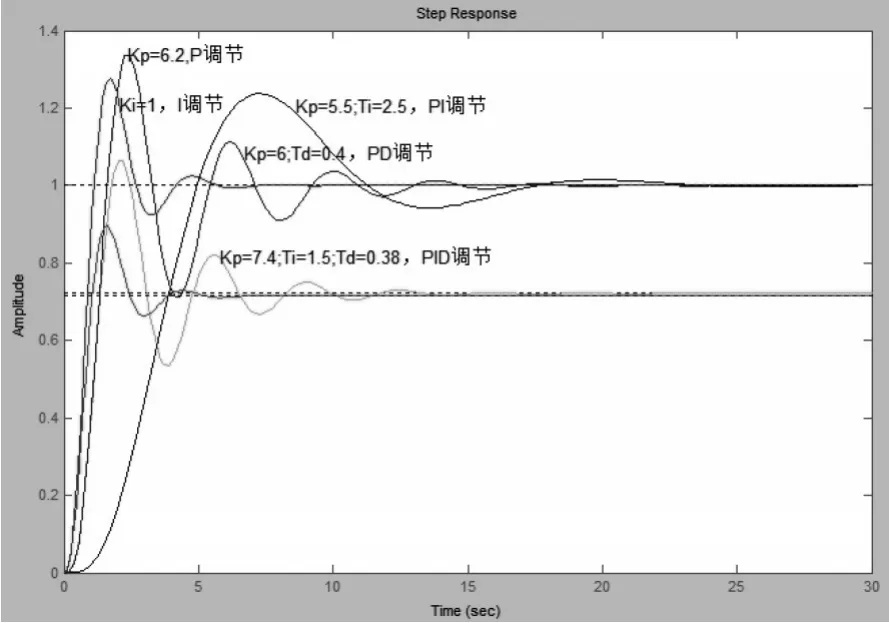
图10 采用不同调节器阶跃响应波形

由图9、图10可知，系统在PD调节器的作用下，系统的动态偏差最小，由于有微分作用，比例增益可增大，缩短调节时间，但无积分作用，系统仍有余差，比例增益增加，余差仅是比例调节的一半左右；虽然PID调节系统动态最大偏差比PD调节器稍差，但有积分作用，系统无余差，振荡周期延长.综合考虑，本文使用积分分离式PID控制方法达到了很好的效果.

6 旋转自由摆控制系统的调试

旋转自由摆控制系统的实物如图11所示.旋转自由摆的现场调试过程如图12所示.

图12中（a）为自由摆自然下垂，摆杆通过不断摇摆增大角度，（b）、（c）、（d）是摆杆起摆的过程，（b）和（c）均为起摆过程的大致角度，（d）为摆杆到达顶端范围，（e）为自由摆完成起摆，摆杆直立.

在自由摆完全直立，下面的旋臂旋转以保持其在这段时间摆杆直立.当外部施加干扰，摆杆通过旋臂的旋转，编码器的不断采样摆杆位置，消除干扰保持摆杆直立.图13所示为旋臂运动，摆杆消除干扰，系统保持倒立.

图11 旋转自由摆实物图

图12 自由摆的调试

图13 自由摆的外界干扰

7 总结

自由摆是一种复杂、时变、强耦合、非线性的高阶自然不稳定系统，是研究控制理论的理想平台，许多控制理论概念通过自由摆实验来表现.本文基于STM32的旋转自由摆控制系统，建立了旋转自由摆的数学模型，通过PID控制算法，验证了其在旋转自由摆实验系统中的有效性，通过测试与理论分析对比调节参数，达到了较好的测试效果.

［1］FURUTA K,OCHIAI T,ONO N.Attitude control of a triple inverted pendulum［J］.Int J Contr,1983,39(6):1351-1365.

［2］孙灵芳.自由摆系统及研究现状［J］.机床与液压，2008，36（7）：306-313.

［3］陆斌，郭燕飞.基于C8051F020单片机的简易旋转自由摆系统［J］.工业控制计算机，2014，27（2）：123-124.

［4］姜倩，管凤旭.旋转式自由摆的镇定和摆起控制的研究［J］.哈尔滨商业大学学报（自然科学版），2007，23（3）：322-324.

［5］程俊，王永，黄南晨，等.旋转式自由摆计算机控制系统［J］.电机与控制学报，2001，5（4）：277-280.

［6］李志民.基于单片机的自由摆控制系统设计与实现［D］.长沙：中南大学，2006：5.

［7］张小明.旋转自由摆系统控制方法的研究［D］.天津：天津大学，2005.

［8］李凌，袁德成，井元伟.旋转式自由摆系统控制策略研究［J］.实验室研究与探索，2006（1）：21-23，46.

［9］包敬海，覃贵寿.基于STM32和增量PID的旋转自由摆的设计［J］.钦州学院学报，2013，28（11）：10-14.

［10］王招治.基于MATLAB的旋转倒立摆的控制与仿真分析［J］.机电技术，2012（4）：36-39.

A Study of a Free Pendulum Control Method

HU Jianqiu1,MAO Limin1,LU Zhenli1,2,ZHU Peiyi1
（1.School of Electrical and Automation Engineering,Changshu Institute of Technology,Changshu 215500,China; 2.IEETA,University of Aveiro,Aveiro,3810-193,Portugal)

Taking the rotating free pendulum as the research object,the systematic mathematical model is established in this paper by analyzing and validating the system stability and controllability and observability.On this basis,the paper proposes an experimental hardware platform based on STM32.The platform adopts a stepper motor to drive the free pendulum.The use of photoelectric encoder measures the rotation angle of the swinging rod. The PID control algorithm is used to realize the motion control of the free pendulum.Besides,the swing of the free pendulum,the swing stability and stabilization are analyzed.The experimental results show that the rotating free pendulum control system designed in this paper runs stably and has a certain anti-interference ability.

inverted pendulum;PID;STM32;MATLAB/Simulink Simulation

TP368

A

1008-2794（2017）02-0068-06

声明

《常熟理工学院学报》编辑部

2016-03-08

苏州市科技计划项目“基于脑机接口技术的康复机器人研究”（SYG201504）

毛丽民，高级实验师，硕士，研究方向：机器人目标跟踪，E-mail：maolimin_1981@163.com.

本刊已许可中国学术期刊（光盘版）电子杂志社在中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。该著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我部上述声明。