基于改进的核主成分法的应用
2017-04-12谷伟伟
谷伟伟
(中国矿业大学理学院,江苏 徐州 221116)
基于改进的核主成分法的应用
谷伟伟
(中国矿业大学理学院,江苏 徐州 221116)
通过计算机调试给出了一个合理的核参数,从而建立了一个核主成分模型.然后用核主成分法对2010年江苏省13个市的居民生活水平进行分析,并和主成分分析结果作了对比,发现改进后的核主成法分析的结果更加合理.最后对江苏未来居民生活水平的改善提出了一些合理的建议,供有关部门参考.
主成分分析;核主成分分析;SPSS;MATLAB
主成分分析已广泛地应用于各个领域.文献[1-2]给出了主成分法在人脸识别中的应用.但主成分分析也有自身的局限,有时候数据间的相关性不是很强,这时变量间就呈现出非线性的关系.核主成分分析是主成分分析的推广,它能处理一些非线性问题.文献[3]给出了相关结论的证明.文献[4-9]给出了核主成分分析在不同领域中的应用.本文在上述文献的基础上,通过MATLAB调试出了一个合理的参数(许多文献是凭经验给定参数),并分析了原因,最后给出一种简便算法,进而算出得分.之后和主成分分析结果相对比,发现核主成分分析的结果较好,提高了综合评价的合理性.
1 预备知识
1.1 主成分模型
设原始样本为x1,x2,…,xn.xk∈Rp,k=1,2,…,n(即p个变量,n个样本).对数据进行中心化后的协方差阵为因为C是实对称矩阵,所以它必可正交对角化.
设λ1,λ2,…,λr,0,…,0为C的p个特征值,不失一般性λ1≥λ2≥…≥λr>0.C的正交标准化特征向量构成的矩阵为L=(l1,l2,…,lp).即有
1.2 核主成分模型
作一个映射ϕ,ϕ: Rp→F,进而空间F中的样本为φ(x1),φ(x2),…,φ(xn),则中心化后的协方差阵为

(1)(2)都要求λ≠0,不同点是(2)式中K的特征值一定不为0,而(1)式则不能说明K的特征值一定不为0,但我们感兴趣的是K的特征值不为0的情况.
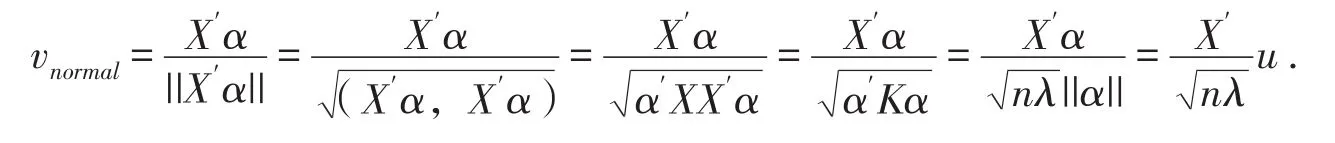
其中u=αnormal.
由文献[3]知样本主成分是样本和特征向量的内积,或是样本在正交标准化特征向量上的投影.利用这个思想,我们算出F空间中的样本主成分,即用F中的样本和标准化特征向量v作内积.
不难证明:这里的ti即为K的第i个特征向量乘上对应的nλi.由于ϕ是未知的,因此<ϕ(xi),ϕ(x)>不好求,这里用多项式核函数来代替内积.
经过MATLAB一系列调试,发现:当d=1,2,…8时,K的方差贡献率都不到90%;当d=9时,贡献率为93.5%;当d>9时,尤其是当d取较大的数时,虽然第一特征值的方差贡献率非常大,但是最大特征根所对应的特征向量中的分量会趋于相同,无法进行样本的比较.
原因分析:随着d取值的增大,矩阵K中的元素会很快变大,而MATLAB中的数据是以科学计数法的形式呈现的.在矩阵K中,n×n个元素是差别很大的,如果它们都除以最大元素的数量级,那么有的较小的元素会变为0.000 0(不为0).这样的话,K中的很多正特征根会不断变为0.000 0,就容易出现K中的某些行元素会趋于相同,从而导致特征向量中的大部分分量相同而无法比较.
2 实例分析
本文选取的数据直接来自《江苏省统计年鉴2011》中7个反映居民生活水平的指标,具体指标如下:
x1:城镇居民人均可支配收入(元);x2:农村人均纯收入(元);x3:年末居民储蓄存款余额(万元);x4:城镇居民人均居住面积(平方米);x5:农村居民人均居住面积(平方米);x6:城镇居民恩格尔系数(%);x7:农村居民恩格尔系数(%).
恩格尔系数表示食物支出占总消费之比,它越大表明越不富裕,因此x6和x7是负向化指标,所以应该将它们正向化,即在原始的x6和x7上同时乘以-1.为了消除量纲的影响,我们对原始数据进行标准化,标准化后的变量记为ZX1—ZX7(见表1).
经过SPSS计算,KMO值为0.63,说明不太适合进行主成分分析.非零特征根为4.629,1.366,第一方差贡献率为66.123%,且方差累计贡献率仅为85.635%(图表略),因此这儿要取2个主成分.
下面用核主成分法分析.采用核函数kij=[
一般情况下ϕ(x1),ϕ(x2),…,ϕ(xn)不一定是中心化的,可以做个变换其中B是一个n×n矩阵,元素都是,具体见文献[10].下面算法中的T和K分别表示上文的K和.
MATLAB中的具体算法是
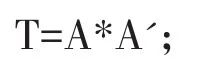

K的非零特征值为1.881 3,0.118 3,0.005 4,0.003 6,0.002 0,0.001 5,0.000 4,0.000 2,第一特征贡献率就达到93.5%,因此这里只要取第一主成分即可.
将以上两种方法的计算结果放在一起对比分析,见表2.
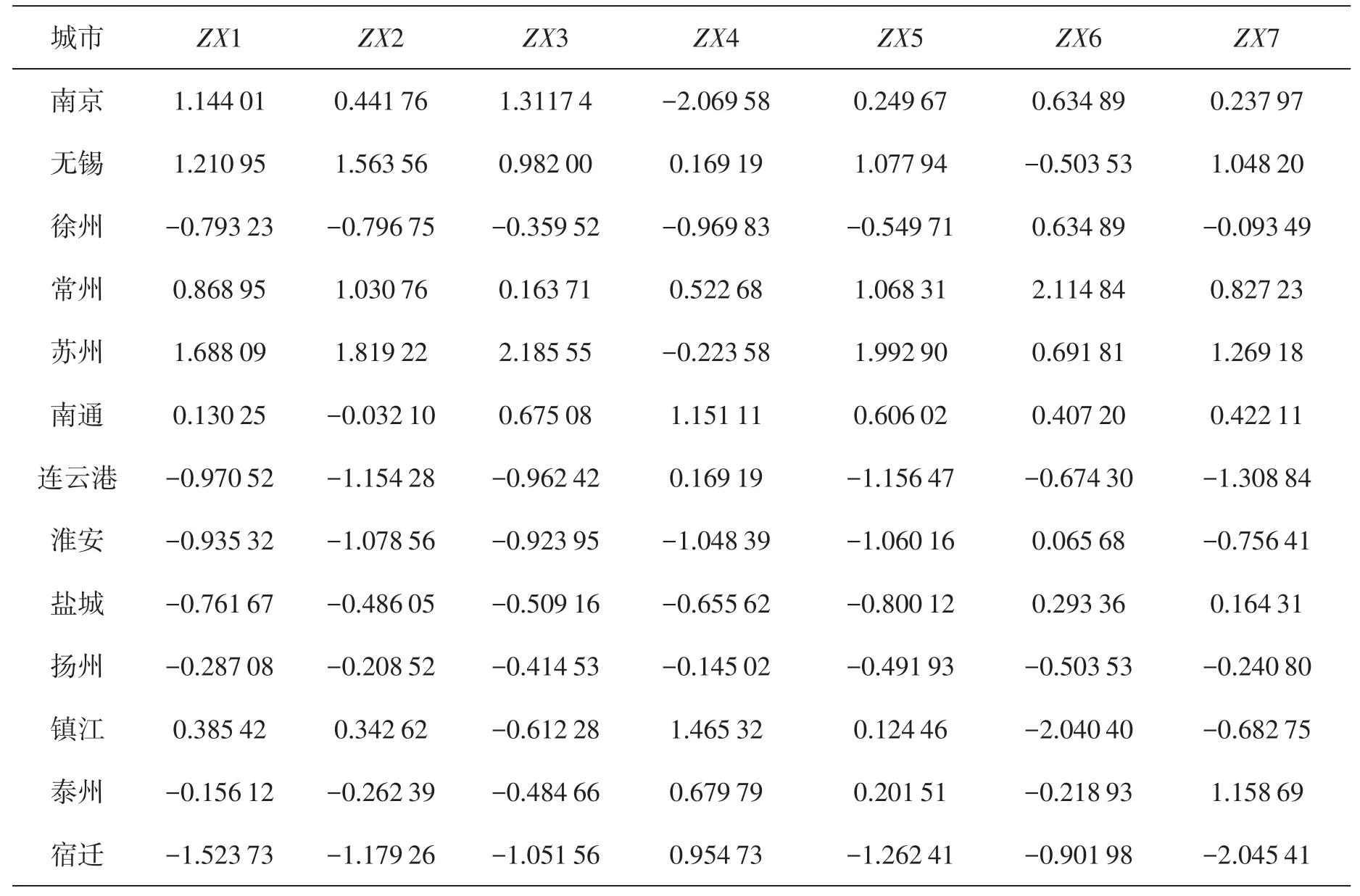
表1 标准化后的数据
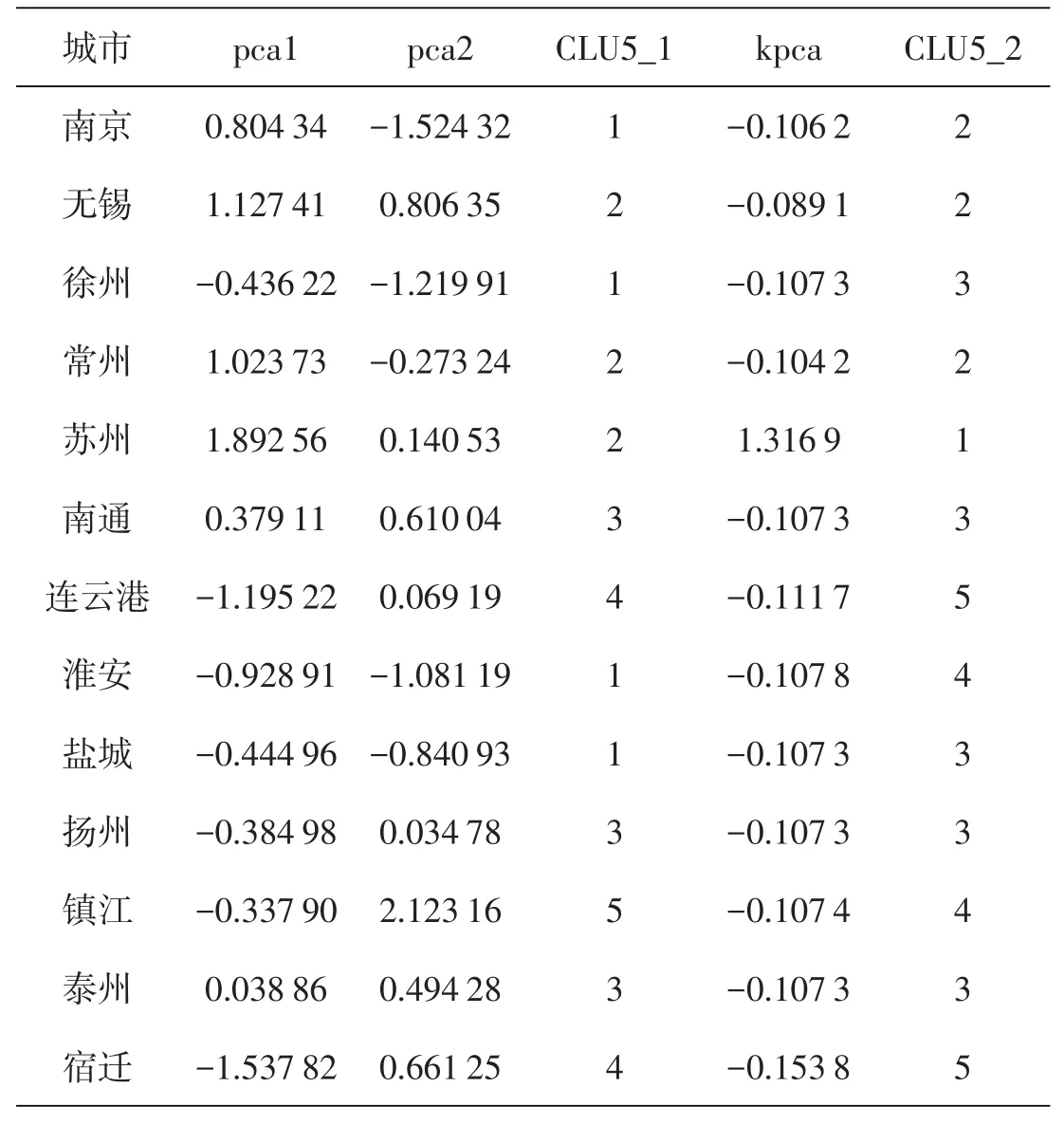
表2 两种方法的结果对比
3 分析
CLU5表示用聚类方法将样本分为5类. CLU5_1是主成分法分类的结果;CLU5_2是用核主成分法分类的结果.
在CLU5_1中:南京、徐州、淮安、盐城分在一起是不妥的,因为南京是省会,位于苏南,而徐州、淮安、盐城都是苏北的城市.南京的综合发展实力远远超过徐、淮、盐;镇江没有什么突出的地方,不应该单独为一类,相反,苏州经济发展强势,更应脱颖而出.综上,CLU5_1分类的结果不太合理.
在CLU5_2中:苏州单独一类,苏州经济发展一直较快,在各个方面都有一定的优势;南京、无锡、常州分为一类,但这类在x4上的得分不高,尤其是南京最低,因此要合理控制好房价,改善人民的居住条件;南通、徐州、盐城、扬州、泰州分为一类,其中因为徐州人口较多,所以徐州在x4和x5上得分较低,因此政府应该努力提供保障性住房;淮安、镇江分为一类,其中苏南的镇江得分最低,主要原因是恩格尔系数过高,导致镇江在x6和x7上的得分较低,因为镇江人舍得在食品上面消费.因此,今后政府可以鼓励百姓在其他方面增加消费,如精神上的消费;连云港、宿迁分为一类,这一类在x1,x2,x3上得分都比较低,因此要大力发展经济,切实提高人民的收入水平.对整个江苏省而言,政府应该在各个方面加大对苏北的投入,增加人民收入,因为没有苏北的腾飞,就没有整个江苏的腾飞.
之所以出现CLU5_1不合理的现象,是因为用SPSS做主成分分析时,由于变量间的相关系数不大,导致KMO值较小,另外,提出的两个主成分一共才包含了原始数据的85.6%的信息,而核主成分提出的第一主成分所含的信息就达93.5%.
最后应该指明,并不是主成分分析处理的结果都不理想,这要依据具体的数据而定,主成分分析处理时要求KMO值尽可能大,数据间有较强的相关性,而核主成分分析比较适合处理非线性的数据.
[1]RAJKIRAN G,VIJAYAN K A.An improved face recognition technique based on modular PCA approach[J].Pattern Recognition Lett,2004,25(4):429-436.
[2]YANG J,ZHANG D.Two-dimensional PCA:A new approach to appearance-based face representation and recognition[J].IEEE Trans Pattern Anal Machine Intell,2004,26(1):131-137.
[3]谷伟伟,王兰,芦凌飞.核主成分法的应用[J].常熟理工学院学报,2013,27(4):20-23.
[4]徐义田,王来生.核主成分分析在企业经济效益评价中的应用[J].数学的实践与认识,2006,36(1):35-38.
[5]杨道军.核主成分分析法在生态经济可持续发展评价中的应用[J].环境科学与技术,2007,30(12):91-93.
[6]李明月,任九泉.基于核主成分分析和加权聚类分析的综合评价方法[J].统计与决策,2010,16:158-160.
[7]肖慧,刘苏东,黄小燕,等.基于核主成分的神经网络集合预报建模研究[J].计算机仿真,2010,27(12):163-166,380.
[8]陈祥涛,张前进.基于核主成分分析的步态识别方法[J].计算机应用,2011,31(5):1237-1241.
[9]程艳秋,迟国泰.基于核主成分分析的生态评价模型及其应用研究[J].中国管理科学,2011,19(3):182-190.
[10]BERNHARD S,SMOLA A,MÜLLER K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J].Neural Computation,1998,10(5):1299-1319.
The Application of Improved Kernel Principal Component Analysis
GU Weiwei
(School of Sciences,China University of Mining and Technology,Xuzhou 221116,China)
This paper selects a proper parameter of kernel function by using computer testing and tries to make a study of the 13 cities of Jiangsu Province in 2010 by building a KPCA model.And it can be found that,compared with that of PCA,the result of KPCA is more reasonable.Besides,by dealing with the underlying causes, some useful suggestions are put forward to improve the living standards of the residents of Jiangsu province, which,at the same time,can be used as a reference for some departments.
principal component analysis;kernel principal component analysis;SPSS;MATLAB
O212.4
A
1008-2794(2017)02-0089-04
2015-06-10
谷伟伟,硕士,研究方向:多元统计,E-mail:864037364@qq.com.
