一类渐近线性Dirichlet边界值问题

高婷梅

（陕西理工大学数学与计算机科学学院，陕西 汉中 723000）

一类渐近线性Dirichlet边界值问题

高婷梅

（陕西理工大学数学与计算机科学学院，陕西 汉中 723000）

利用山路引理和截断技巧，证明了一类Dirichlet边界值问题至少存在一个正解和一个负解.

山路引理；渐近线性；正解；负解

考虑如下带有Dirichlet边界值条件的椭圆型方程：

其中Δpu是p-拉普拉斯算子且p>1，Ω是Rn(n≥1)中带有光滑边界的有界区域.函数满足以下条件：

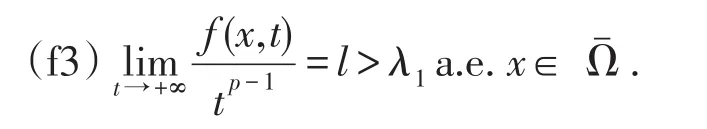
本文的主要结果是：

定理1假设函数f(x,t)满足条件（f1）-（f3），则方程（1）至少存在一个正解.

注由于条件（f3）成立，则称函数f(x,t)在无穷远处是渐近线性的.对于渐近线性Dirichlet边界值问题，前人进行了广泛的研究，如文献［1-5］.文献［2］中，作者假设函数f(x,t)满足条件：

并证明了方程（1）正解的存在性.（h1）是一个比较强的条件，它对函数f(x,t)有很大的约束，于是文献［3］和［4］在没有假设条件（h1）成立的情况下，分别用Fucik谱的理论和山路引理［6］证明了方程（1）至少存在一个正解.虽然前人得到了很多丰富的结果，但是他们有一个共同点，都假设函数f(x,t)在t=0处是渐近线性的，

即f(x,t)满足

若函数f(x,t)满足

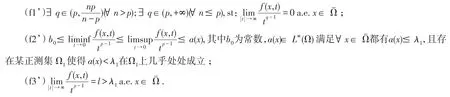
利用截断技巧，可以得到以下结果：

定理2假设函数f(x,t)满足条件（f1’）-（f3’），则方程（1）至少存在一个正解和一个负解.定义如下的C1泛函：

引理1假设函数f(x,t)满足条件

证明由条件（f2），利用文献［7］的结论可知，∃α∈(0,1)，st：

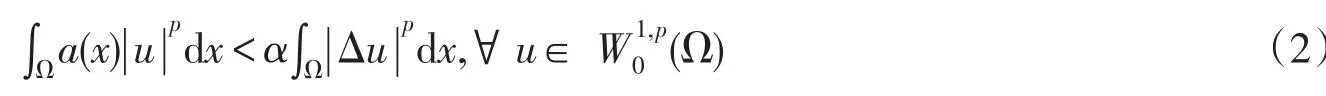
其中C1>0是常数.于是，

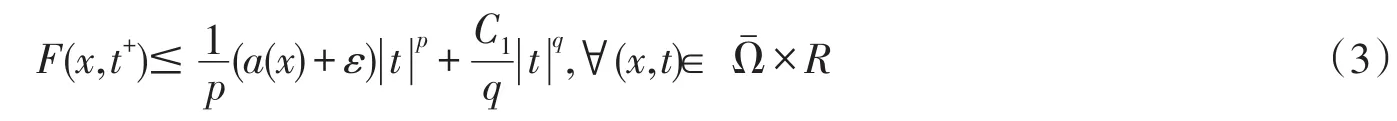
由（2），（3）式，Poincare和Sobolev不等式，有

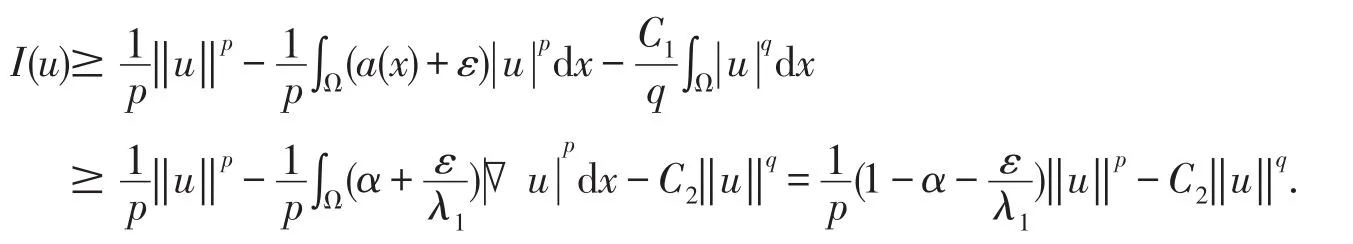
其中，C2>0是常数.则有

引理2假设函数f(x,t)满足条件（f3），则（见文献［2］引理2.3）.

引理3假设函数f(x,t)满足条件（f2）-（f3），则I满足（PS）条件.

证明令满足

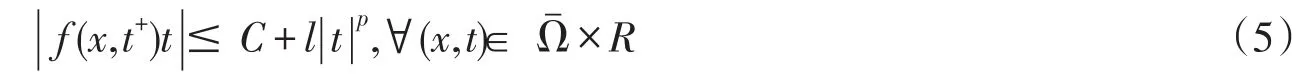
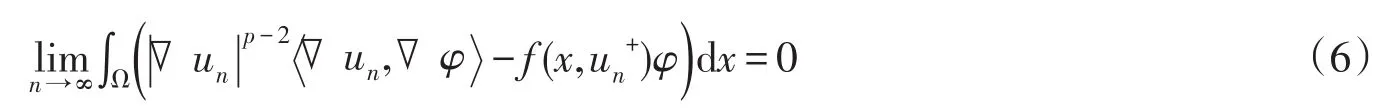
在（6）式中，令φ=un，则由（4），（5）式，得

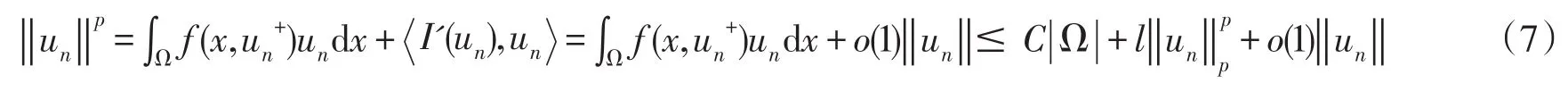
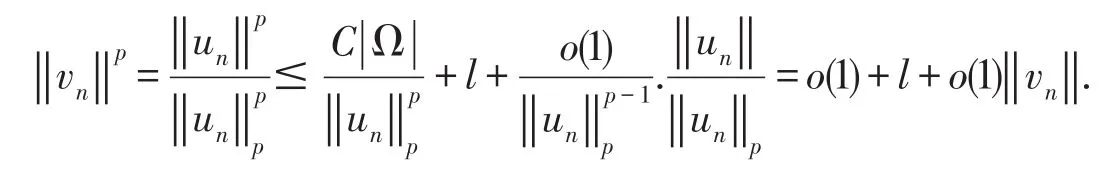
所以，由（6）式，得

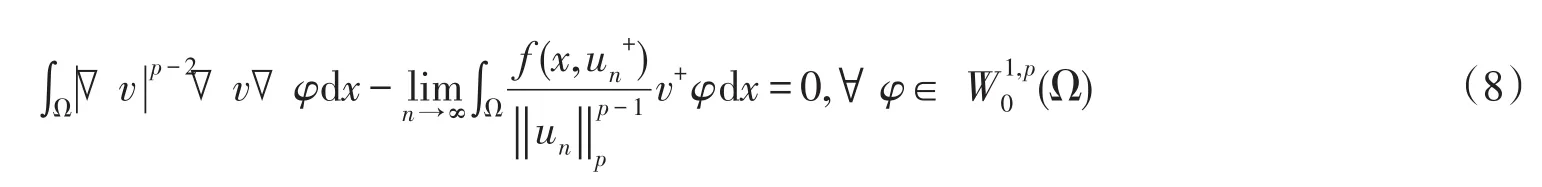
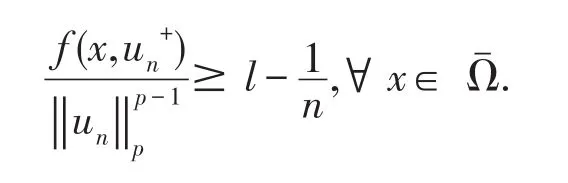
故

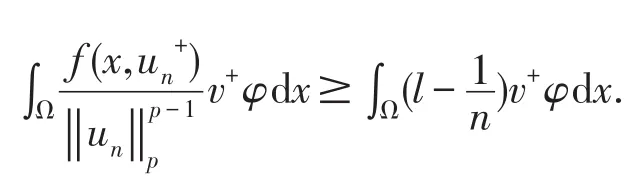
令n→∞，可得

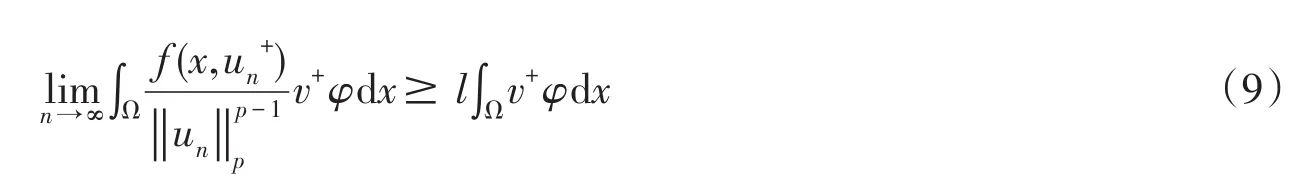
由（8），（9）式，有

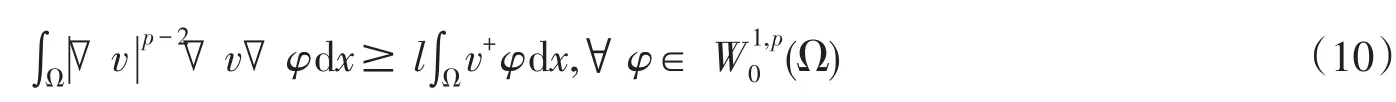
因为λ1是-Δp的第一个特征值，设φ1是λ1对应的正则特征向量，则由（10）式，得

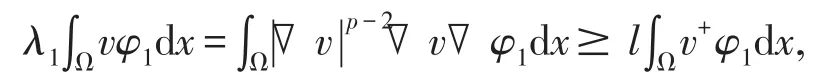
这与l>λ1矛盾.所以有界，从而由（7）式，可知有界.因此存在一收敛子列，即I满足（PS）条件.

定理1的证明众所周知，寻找方程（1）的非平凡解等价于寻找泛函I(u)的非零临界点.由引理1～引理3，利用山路引理，泛函I有一个临界点u满足I(u)≥β>0，但由条件（f2），f(x,0)=0，则I(0)=0，所以u≠0，从而u是方程（1）的一个非平凡解.因为

定理2的证明首先考虑如下截断问题

其中，

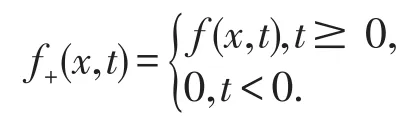
由f+的定义可知f+满足定理1的条件，故由定理1，方程（11）存在一个正解u>0，它也是方程（1）的解.然后再考虑以下截断问题

其中，

为了求得方程（12）的解，令v=-u,g(x,t)=-f-(x,-t)，则方程（12）等价于以下方程）

易见如果v是方程（13）的解，则u=-v是方程（12）的解.因为f满足条件（f1’）-（f3’），故由g的定义，可知g满足条件（f1）-（f3），从而，由定理1，知方程（13）存在一个正解v>0，所以u=-v<0是方程（12）的解，同时也是方程（1）的解.因此，方程（1）至少存在一个正解和一个负解.

［1］ZHOU H S.Existence of asymptotically linear Dirichlet problem［J］.Nonlinear Analysis，2001，44（7）：909-918.

［2］LI G,ZHANG Z,Zhou H S.Asymptotically linear Dirichlet problem for the p-Laplacian［J］.Nonlinear Analysis,2001,43(8): 1043-1055.

［3］ZHANG Z,LI S,FENG W.On an asymptotically linear elliptic Dirichlet problem［J］.Abstract and Applied Analysis,2002,7(10): 509-516.

［4］何万生，裴瑞昌.P-Laplacian方程的渐近线性Dirichlet问题［J］.河北师范大学学报，2006，30（1）：21-24.

［5］裴瑞昌.P拉普拉斯Dirichlet问题的非平凡解［J］.数学物理学报，2013，33A（1）：165-173.

［6］MAWHIN J,WILLEM M.Critical point theory and Hamilton Systems［M］.New York:Springer-verlag,1989.

［7］WANG J,TANG C L.Existence and multiplicity of solutions for a class of superlinear p-Laplician equations［J］.Bound Value Probl,2006,12(1):1-12.

［8］VAZQUEZ J L.A strong maximum principle for some quasilinear elliptic equations［J］.Applied Mathematics and Optimization, 1984,12(3):191-202.

A Class of Asymptotically Linear Dirichlet Boundary Value Problem

GAO Tingmei
(School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong 723000,China)

Using the Mountain pass lemma and a truncation technique,the author of this paper obtains a positive solution and a negative one for a class of asymptotically linear Dirichlet boundary value problem.

mountain pass lemma;asymptotically linear;positive solution;negative solution

177.91

A

1008-2794（2017）02-0085-04

2016-04-25

陕西理工大学科研基金项目“变分法在一类椭圆边值问题中的应用”（SLGKY15-47）

高婷梅，讲师，硕士，研究方向：非线性泛函分析，E-mail：gtmgtmgtm@126.com.